GLOBAL EXISTENCE AND OPTIMAL CONVERGENCE RATES OF SOLUTIONS FOR THREE-DIMENSIONAL ELECTROMAGNETIC FLUID SYSTEM∗

Yin LI(李银)Ruiying WEI(位瑞英)

School of Mathematics and Statistics,Shaoguan University,Shaoguan 512005,China E-mail:liyin2009521@163.com;weiruiying521@163.com

Zheng-an YAO(姚正安)

Department of Mathematics,Sun Yat-sen University,Guangzhou 510275,China E-mail:mcsyao@mail.sysu.edu.cn

Abstract In this article,we study the electromagnetic fluid system in three-dimensional whole space R3.Under assumption of small initial data,we establish the unique global solution by energy method.Moreover,we obtain the time decay rates of the higher-order spatial derivatives of the solution by combining the Lp−Lqestimates for the linearized equations and an elaborate energy method when the L1-norm of the perturbation is bounded.

Key words electromagnetic fluid;decay rates;Fourier-splitting method

1 Introduction

In this article,we consider the electromagnetic fluid system for the compressible flow

where the unknowns ρ,u=(u1,u2,u3),p,θ,e,ρe,E=(E1,E2,E3)and B=(B1,B2,B3)stand for the density,velocity,pressure,absolute temperature,internal energy,electric charge density,electric field,and magnetic field,respectively.For simplicity,we consider the case that the fluid is a polytropic ideal gas,that is e=CVθ,p=Rρθ with CV>0 and R>0 being the speci fic heat at constant volume and the generic gas constant,respectively.Ψ(u)is the viscous stress tensor given by

Ψ(u):∇u in the third equation of(1.1)denotes the viscous dissipation function

The parametersµ and λ are constants denoting the viscosity coefficients of the flows satisfyingµ >0 and 2µ +3λ >0.The constant µ0>0 and ǫ0>0 are dielectric constant and the magnetic permeability,respectively.I3denotes the 3×3 identity matrix,and∇u⊤the transpose of the matrix ∇u.The electric current density J is described by the Ohm’s law,that is,J= ρeu+σ(E+u×B),where σ >0 is the electric conductivity coefficient.

Despite its physical importance of electromagnetic fluid dynamics,there are only partial results to the electromagnetic fluid dynamics.As pointed out by Kawashima[1],the system of the electromagnetic quantities(E,B,ρe)in system(1.1),which is regarded as a first-order hyperbolic system,which is neither symmetric hyperbolic nor strictly hyperbolic in the threedimensional case.The same difficulty also occurs in the first-order hyperbolic system of(E,B)which is obtained from the above system by eliminating ρewith the aid of the first equation of(1.1)6.Therefore,the classic hyperbolic-parabolic theory cannot be applied here.In[1],Kawashima established the global existence of classical solution to(1.1)in R2provided the initial data is sufficiently close to some constant steady states.In[2],Umeda,Kawashima and Shizuta showed that the decay at the L2-rate(1+t)−34holds for solutions of the linearized equations of electromagnetic fluid dynamics near some given constant equilibria,if the small initial disturbance belongs to L1(R3)∩L2(R3).Some recent related work on large time behavior can be referred to reference[3–5]and so on.

In this article,as it was pointed out by Imai[6],the assumption that the electric charge densityis physically very reasonable for the study of plasmas.And it may be worth-while to note that the assumption ρe⋍ 0 is quite di ff erent from the assumption of exact neutrality ρe=0,which would lead to the super fluous condition divE=0.Based on those assumptions,we can eliminate the terms involving ρein the original system(1.1)and obtain the following simplified system

Initial conditions are given as

with the compatible condition

In this article,we first establish the global solution of the solutions to(1.2)–(1.3)in the whole space R3near the constant equilibrium state by the energy method following the idea of Guo,Wang[7]and Wang[8]under the assumption that the H3norm of the initial date is small,but the higher order derivatives can be arbitrarily large.Then we establish the large time behavior by combining the Lp−Lqestimates for the linearized equations and an elaborate energy method by assuming that the initial data belongs to L1(R3)additionally.

NotationThroughout this article,∂jstands for∂xj,∇lwith an integer l≥ 0 stands for the usual any spatial derivatives of order l.When l<0 or l is not a positive integer,∇lstands for Λlde fined bywhereû is the Fourier transform of u andits inverse.We will employ the notation A.B to mean that A≤CB for a universal constant C>0 that only depends on the parameters coming from the problem.For the sake of conciseness,we write

In this subsection,we first reformulate system(1.2).We setE=E,B=B,then the initial value problem(1.2)–(1.3)can be rewritten as

where

here we have set the constants σ = ǫ0= µ0=1,without loss of generality.

Denote the scaled parameters and constants by

with

and the nonlinear terms have the following equivalent properties

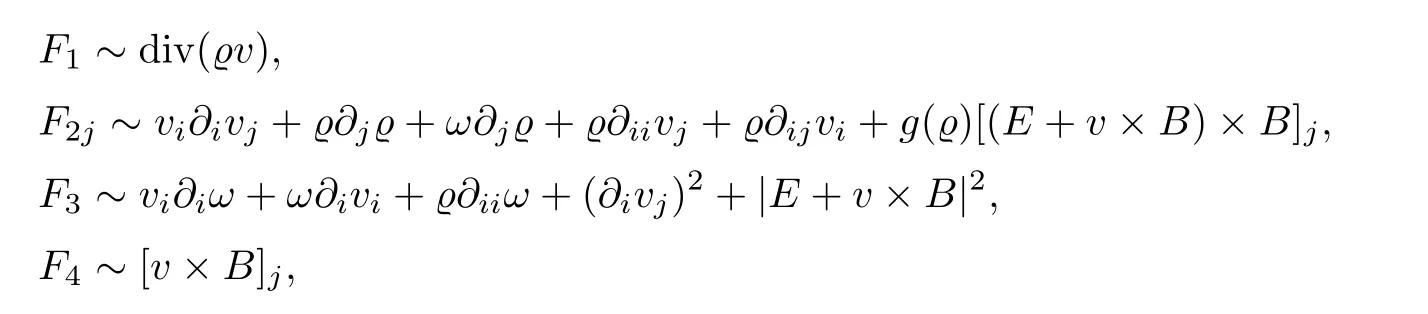
where

Our main results are stated in the following theorem.

Theorem 1.1Let N ≥ 3,assume that(0,v0,ω0,E0,B0) ∈ HNand divB0=0,then there exists a constant δ0>0 such that if

then the problem(1.6)–(1.7)has a unique global solution((t),v(t),ω(t),E(t),B(t))satisfying that for all t≥0,

and for 2≤p≤∞,there holds

especially,

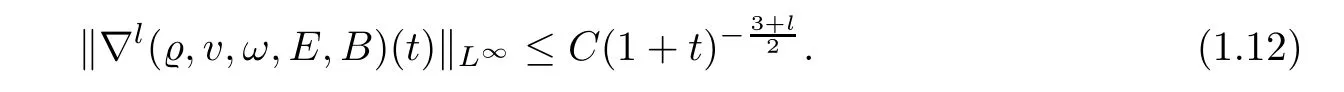
Moreover,for l=0,1,···,N − 2,

2 Energy Estimates

In this subsection,we will derive the a priori nonlinear energy estimates for system(1.6).Hence we assume a priori that for sufficiently small δ>0,

First of all,by(2.1)and Sobolev’s inequality,we obtain

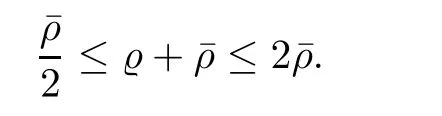
Hence,we immediately have|g(l)()|≤ C for any l≥ 0.

We begin with the first type of energy estimates.

ProofApplyingto(1.6),and multiplying the resulting identities byrespectively,summing up them and then integrating over R3by parts,we get

We shall estimate each term in the right hand side of(2.3).First,for the term I1,by Lemma A.2 and Hölder’s inequality,we obtain

About the term I2,we have

First,for the term I21,employing the Leibniz formula and by Hölder’s inequality,we obtain

where α is de fined by

where α is de fined by

Combining(2.7)and(2.8),by Cauchy’s inequality,we deduce from(2.6)that for 0 ≤ l≤ k,

Similarly,we can bound

And for the term I24,we obtain

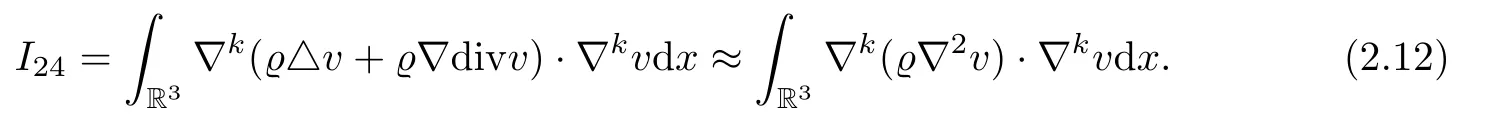
If k=0,we integrate by parts and Hölder’s inequality to get

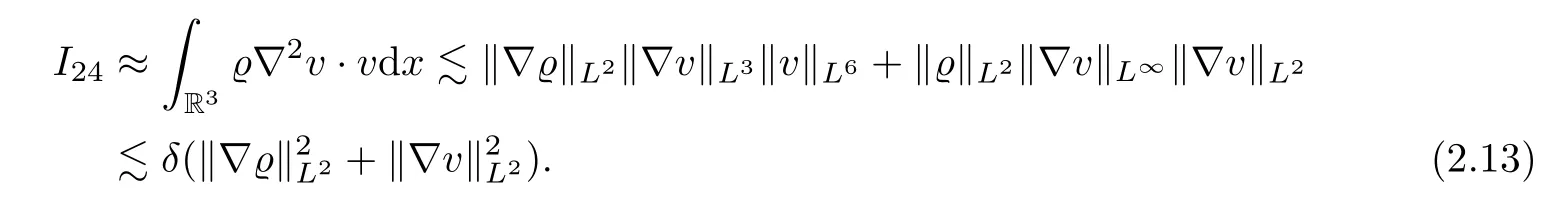
If k ≥ 1,we integrate by parts,then employ the Leibniz formula and Hölder’s inequality,we obtain

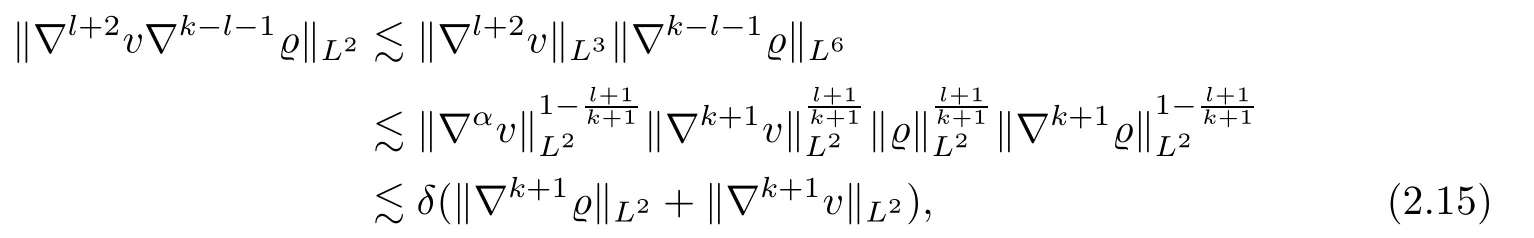
where α is de fined by

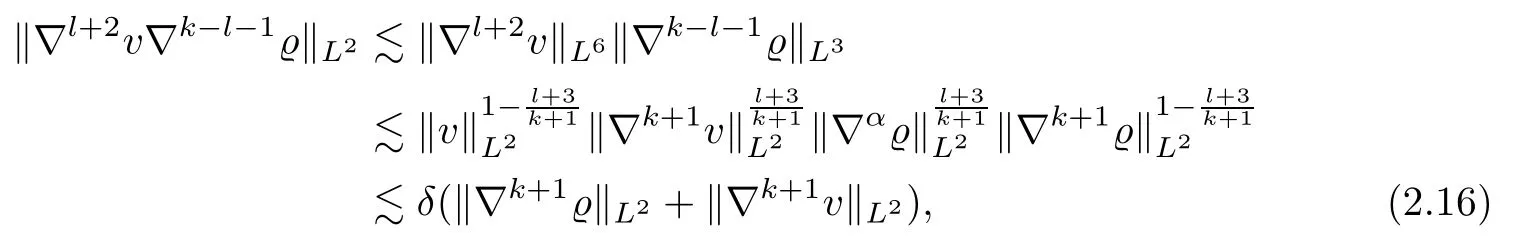
where α is de fined by

Combining(2.13)–(2.16),we deduce from(2.12)that

We now estimate the term I25,we employ the Leibniz formula and Hölder’s inequality,we obtain

By using Lemma A.1 and Lemma 4,we estimate the first factor in the above

Combining(2.19),we deduce from(2.18)that

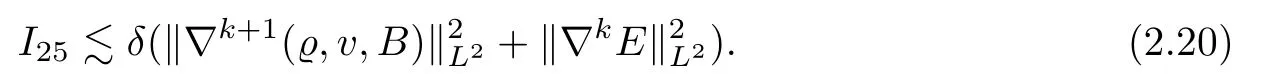
Next,for the term I26,if k=0,we integrate by parts and Hölder’s inequality to get

If k≥1,we integrate by parts and employ the Leibniz formula and Hölder’s inequality,we obtain

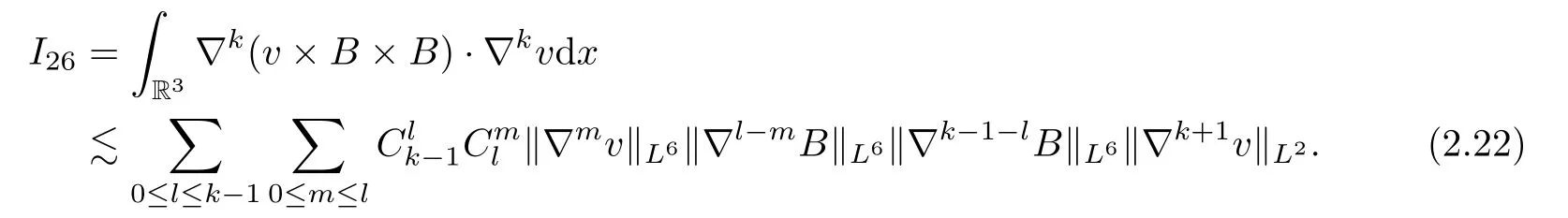
where α is de fined by

where α is de fined by

Combining(2.6)–(2.24),we deduce from(2.5)that

Similar to the estimate of the term I1and I2,for the term I3and I4,we have

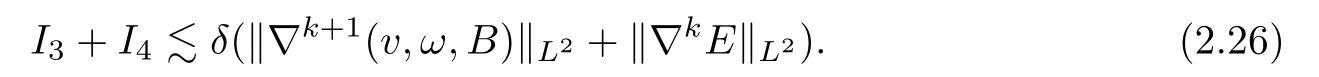
Summing up the estimates for I1−I5,that is,(2.4),(2.25)and(2.26),we deduce(2.3)for 0≤k≤N−1,this yields the desired result. ?

Next,we derive the second type of energy estimates excluding v,ω and E themselves.

Lemma 2.2Ifthen for k=0,···,N − 1,we have

ProofApplyingto(1.6),and multiplying the resulting identities byrespectively,summing up them and then integrating over R3by parts,we get

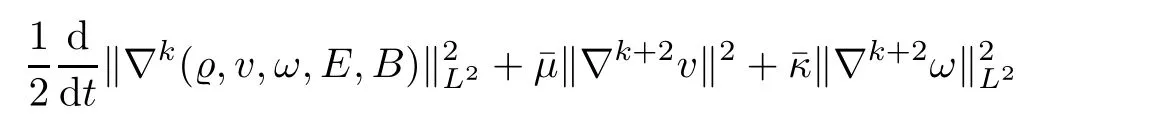
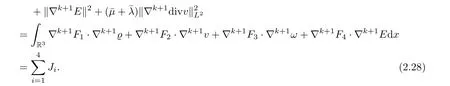
We shall estimate each term in the right hand side of(2.28).

First,for the term J11,employing the Leibniz formula and by Hölder’s inequality,we obtain

For l=0,we have

where α is de fined by

where α is de fined by

Combining(2.31)–(2.33),we deduce from(2.30)that for 0 ≤ l≤ k+1,

For J12,we have

where α is de fined by

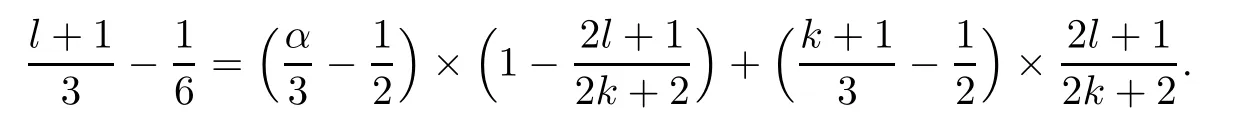
where α is de fined by

Combining(2.36)and(2.37),we deduce from(2.35)that for 0≤l≤k+1,

About the term J2,we have

Similar to the estimate of the term J1,for the term J21−J23,we have

We now estimate the term J24,

If l=0,by fact(2.1)and Hölder’s inequality,we obtain

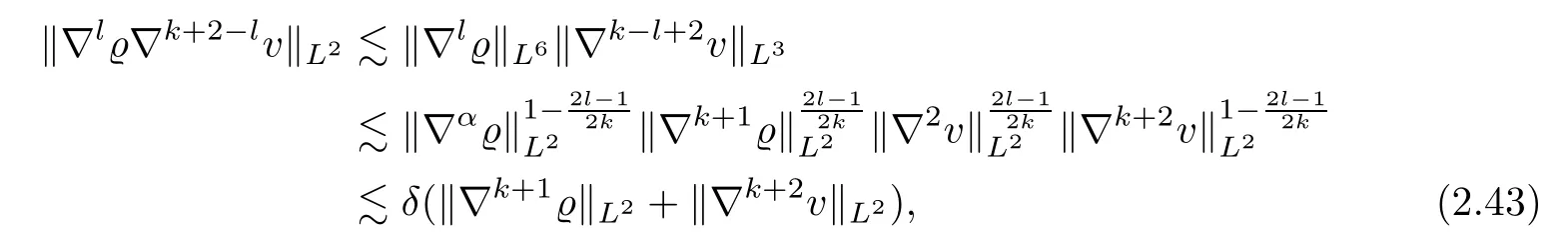
where α is de fined by

where α is de fined by

Combining(2.42)–(2.44),we deduce from(2.41)that for 0 ≤ l≤ k,

Similar to the estimate of the term I24,for the termJ25and J26,we have

Combining(2.40),(2.45)and(2.46),we deduce from(2.39)that

Similar to the estimate of the term J1and J2,for the term J3and J4,we have

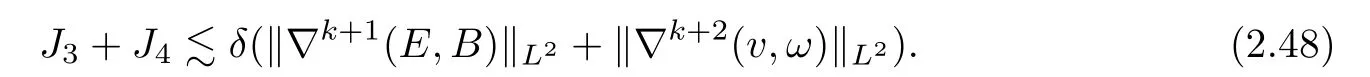
Summing up the estimates for J1−J4,that is,(2.34),(2.38),(2.47)and(2.48),we deduce(2.28)for 0≤k≤N−1,this yields the desired result. ?

The following lemma provides the dissipation estimate for.

ProofApplyingto(1.6)2,multiplyingand integrating by part,we get

where ε is small enough.

For first term in the right-hand side of(2.50),by(1.6)1,integrating by parts for both the t-and x-variables,and by using Lemma A.2,we may estimate

The second term in(2.50)can be estimated as follows

On the other hand,recalling the derivations of the estimates of J2in Lemma 2.2,we have already proved that

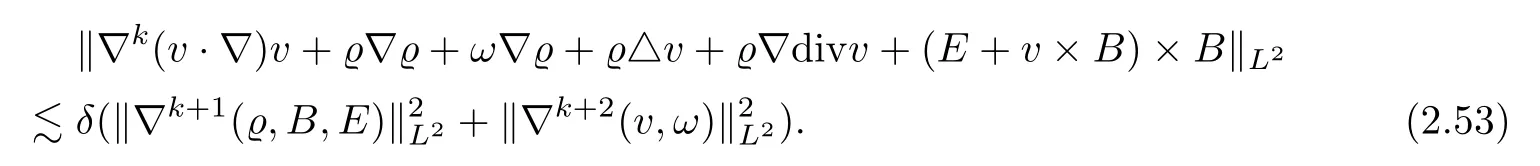
Plugging estimates(2.51)–(2.53)into(2.50),by Cauchy’s inequality,since δ is small,we then obtain(2.49). ?

The following lemma provides the dissipation estimate for B.

ProofApplyingto(1.6)4,multiplyingand integrating by part,we get

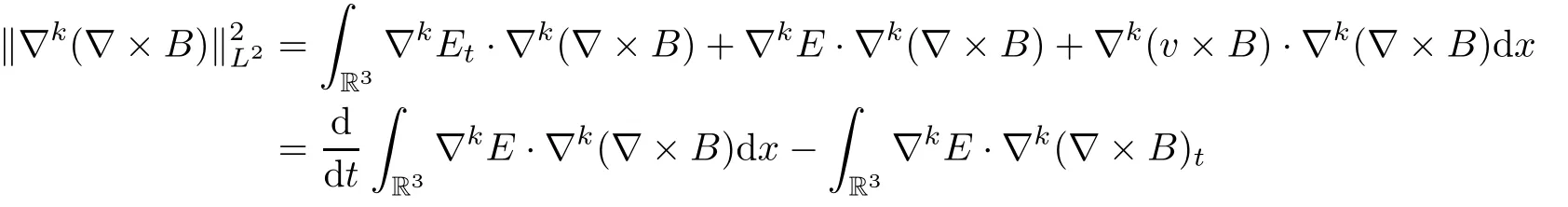
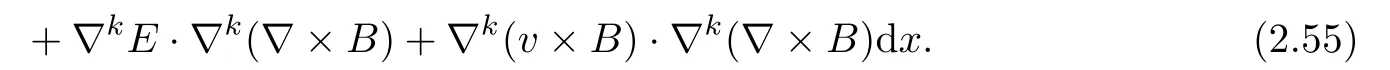
By(1.6)5,we have

Here we employ the Leibniz formula and by Hölder’s inequality to obtain

where α is de fined by

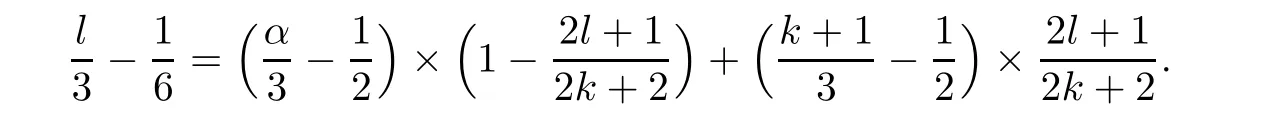
where α is de fined by

Combining(2.58)and(2.59),we deduce from(2.57)that for 0≤l≤k,

Moreover,we have used the fact that the Riesz operatoris bounded from L2to itself,one has

3 The Global Existence of Solution

In this section,we combine all the energy estimates that we derive to prove(1.9)of Theorem 1.1.

Let k=m−1 in estimates(2.27)of Lemma 2.2,we have

Adding inequality(3.2)with(3.1),we get

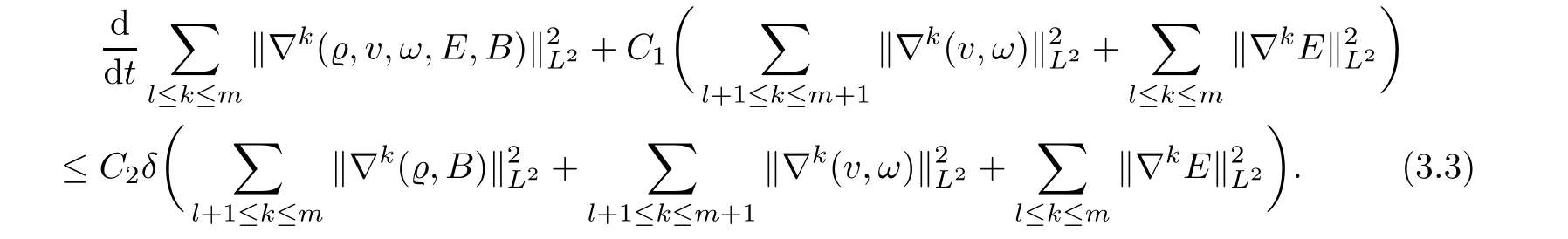
Summing up estimates(2.49)of Lemma 2.3 for from k=l to m−1,we have

Summing up estimates(2.54)of Lemma 2.4 for from k=l to m−1,we have

Adding inequality(3.5)with(3.4),we get

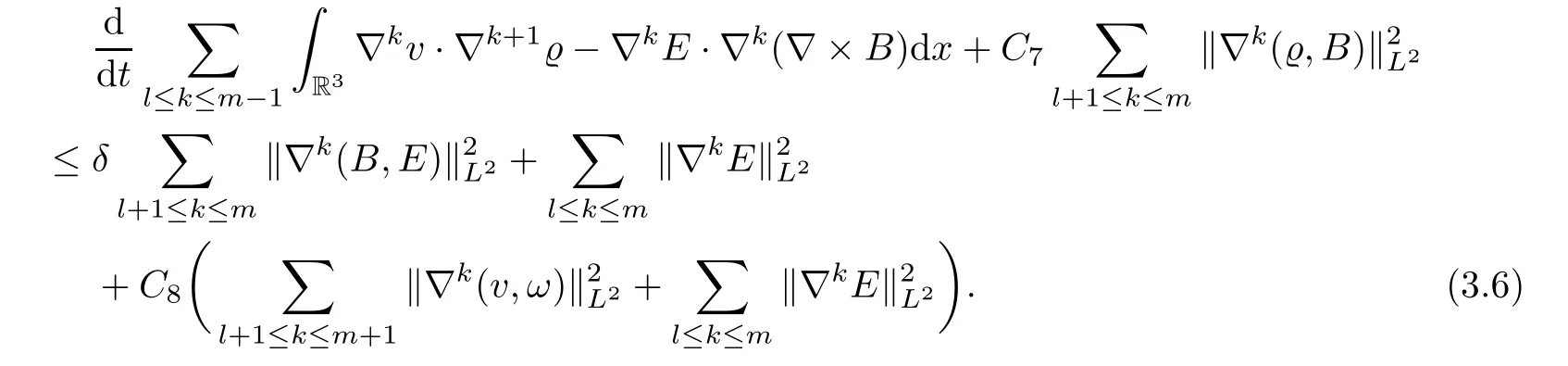
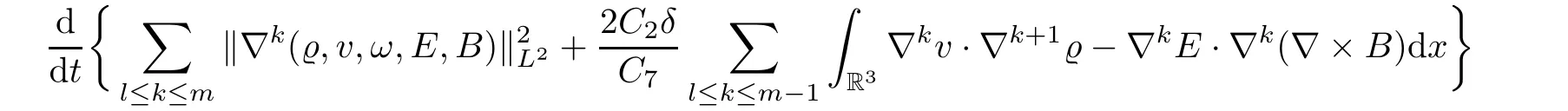
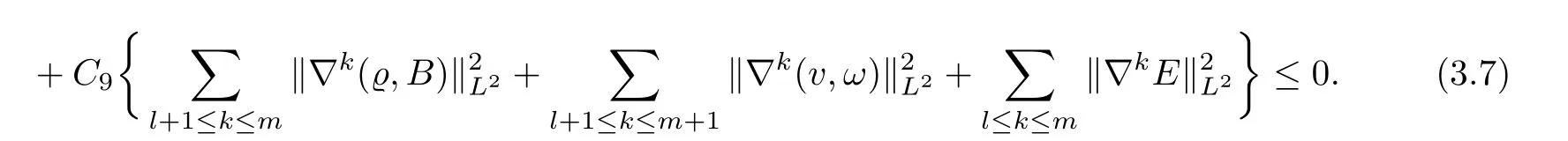
Then we may write(3.7)as that for 0≤l≤m−1

Proof of(1.9).Taking l=0 and m=3 in(3.9),and then integrating directly in time,we get

By a standard continuity argument,this closes the a priori estimates(2.1).This in turn allows us to take l=0 and m=N in(3.9),and then integrate it directly in time to obtain

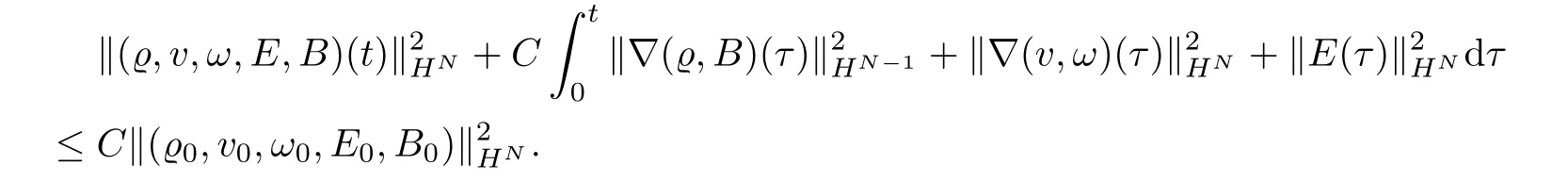
This proved(1.9).

4 Convergence Rate of the Solution

The aim of this section is to establish the decay rates of the solution stated in Theorem 1.1 under additional assumptions that the initial data belong to L1.First,we give the decay rates for the linearized electromagnetic fluid system.Then,we establish the decay rates for the flows(1.6)by the method of Fourier-splitting method and energy estimates.The Cauchy problem to the linearized electromagnetic fluid system is as follows

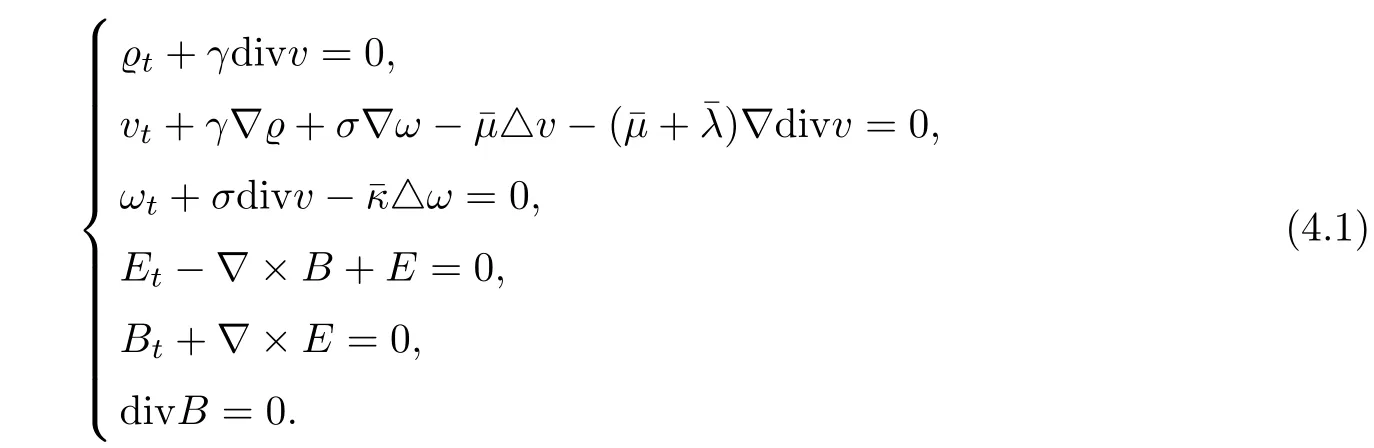
Initial data of the system is given as

Next,we consider the time decay property of solutions for the following two systems

and

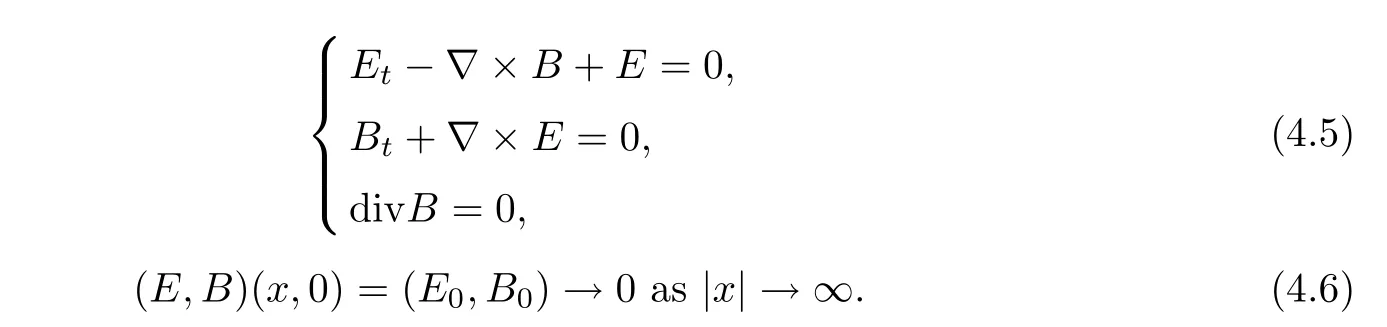
For the system(4.3)and(4.4),use A to denote the following matrix-valued di ff erential operator

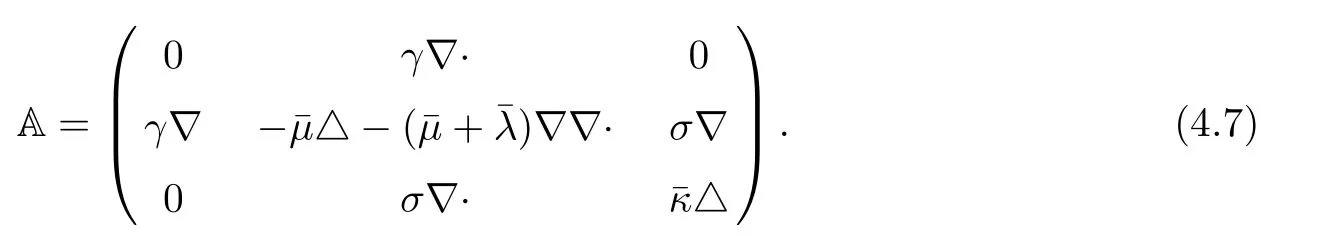
Then the corresponding semigroup generated by the linear operator−A is

For simplicity of notation,set U(t)=(,v,ω)(t)and F(U)=(F1,F2,F3)(U).Then the reformulated problem(4.3)and(4.4)can be written both as

and as the integral form

As in[9,10,14],making use of the semigroup theory for evolutional equation,the solutions U of the linear Cauchy problem(4.3)and(4.4)have the following Lp−Lqestimates.

Lemma 4.1Let k≥0 be an integer and,then for any t≥0,the solution U(t)of system(4.3)satis fies

Moreover,the time decay property of system(4.5)and(4.6)was studied extensively,cf.[11–13].

Lemma 4.2Let k≥0 be an integer and,then for any t≥0,the solution U(t)of system(4.3)satis fies

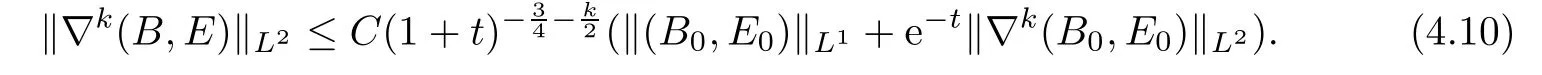
Now,we turn to establish the time decay rates for the electromagnetic fluid(1.6).

Lemma 4.3Under the assumptions of Theorem 1.1,the global solution(,v,ω,E,B)of problem(1.6)satis fies

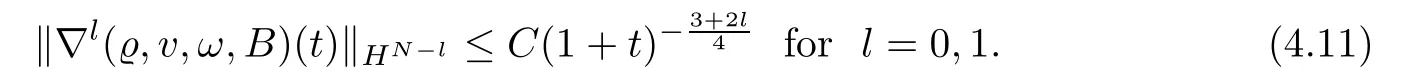
ProofAddingto both sides of(3.9)gives

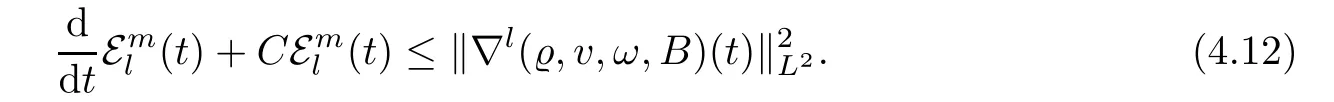
Taking l=1 and m=N in(4.12),we get

It follows from Gronwall inequality and Lemma 4.1 that

In order to derive the time decay rate forwe need to control the term

First,for the nonlinear terms of model(1.6),employing the Hölder’s inequality,Lemma A.1 and Lemma A.2,we get

Then,Lemma 4.1 and Lemma 4.2 together with Duhamel principle,we have

Inserting(4.16)into(4.14),it follows

where we have used the fact

Noticing the de finition of M(t),we get

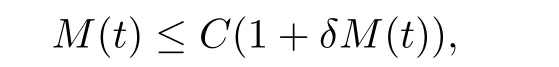
which implies

since δ>0 is sufficiently small.Hence,we have the following decay rates

On the other hand,by(4.15),it is easy to deduce

where we have used the inequality[14]

which together with(4.19)implies(4.11).

Lemma 4.4Under the assumptions of Theorem 1.1,the global solution(,v,ω,E,B)of problem(1.6)satis fies

ProofWe are ready to prove(4.21)by induction.When l=0,1,inequality(4.11)is established in Lemma 4.3,suppose(4.21)holds for the case l=k −1,and k=2,3,···,N −1,that is

We need show(4.21)holds for l=k.Let l=k and m=N in estimates(3.9),we have

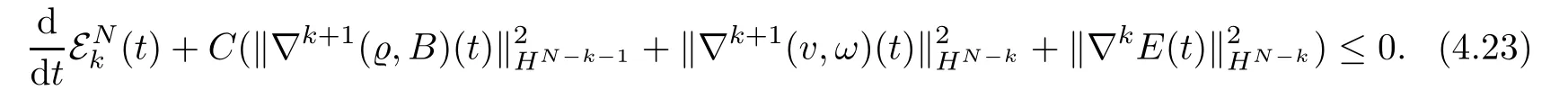
As in[15],we de fine

for a constant a that will be speci fied bellow.Then

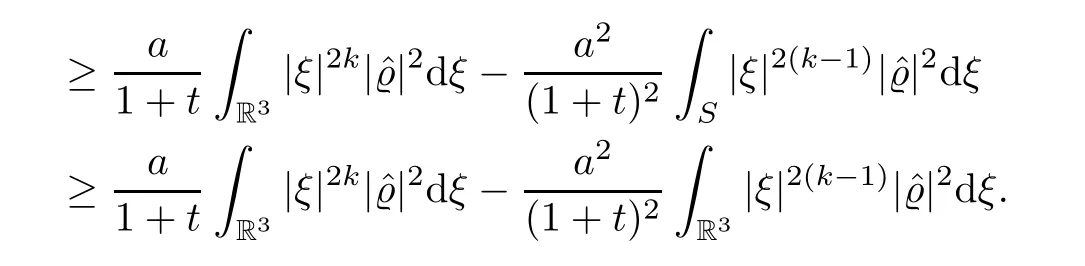
Thus,we have

Similarly,one has

and

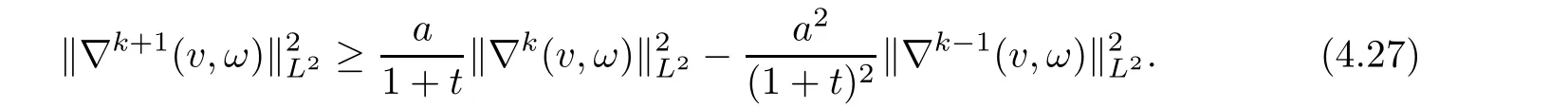
Summing up estimates(4.27)for k from k to N,one has

Substituting inequalities(4.25),(4.26),(4.28)into(4.24),applying(4.22),it follows

where we have used

and

for some sufficiently large time t≥a−1 such that

This,together with the de finition ofimplies that

Choosing

and multiplying both sides of(4.29)by(1+t)k+2,we get

Solving the inequality direcly yields

Hence,we verify that(4.21)holds on for the case l=k,this concludes the proof of the lemma. ?

With Lemma 4.3 and Lemma 4.4 in hand,we are ready to proof Theorem 1.1.

ProofWith the help of Lemma 4.3 and Lemma 4.4,it is easy to obtain conclusion(1.10).As for(1.11),by(1.10)and the Gagliardo-Nirenberg inequality,

the claim follows.

As for(1.13), first of all,we shall estimate.For l=0,···,N − 2,applying ∇lto(1.6)1,multiplying the resulting identities by ∇ltand integrating the resulting equation over R3,one gets

We shall estimate each term in the right hand side of(4.32).First,for the term K1,by Lemma A.2 and Young’s inequality,we obtain

where ε is small enough.

Similarly,we can bound

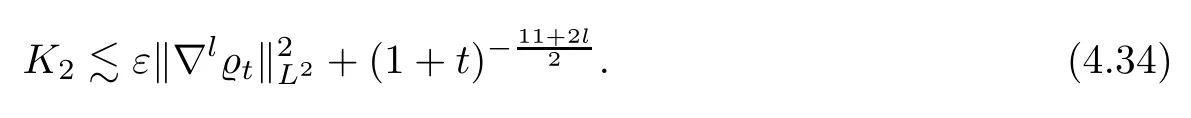
Using Young’s inequality,K3can be estimated as follows

Combining(4.33)–(4.35),we deduce from(4.32)that

By using Lemma A.2 again,we estimate the second factor in inequalities(4.37)

By employing the Leibniz formula,Hölder’s inequality,Young’s inequality and Lemma A.2,we estimate the third factor in inequalities(4.37)

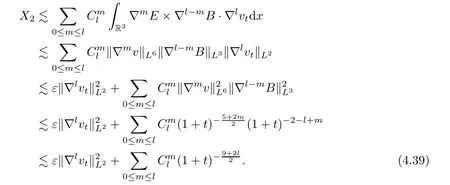
Similar to the estimate of the term X2,for the term X3,we have

Combining(4.38)–(4.40),we deduce from(4.37)that

Similar to the estimate of the term k∇lvtkL2,we have

and

Thus,(1.13)is proved.The proof of Theorem 1.1 is completed.

Appendix A Analytic Tools

We will extensively use the Sobolev interpolation of the Gagliardo-Nirenberg inequality.

Lemma A.1Let 0≤m,α≤l,then we have

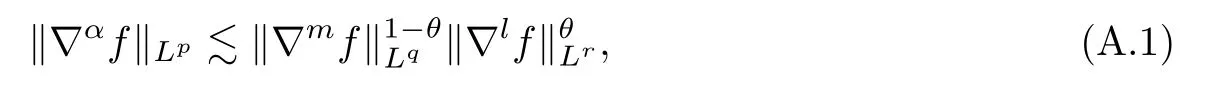
where 0≤ θ≤ 1 and α satis fies

Here when p=∞we require that 0<θ<1.

ProofThis can be found in(see[16],p.125,Theorem).

We recall the following commutator estimate.

Lemma A.2Let m≥1 be an integer and de fine the commutator

Then we have

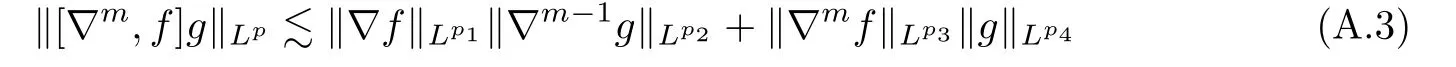
and for m≥0

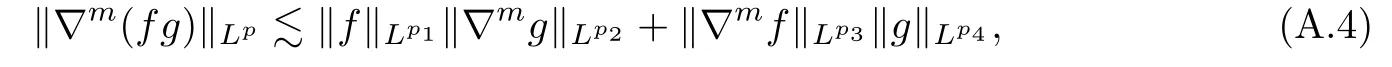
where p,p2,p3∈ (1,∞)and

ProofFor p=p2=p3=2,it can be proved by using Lemma 2.1.For the general cases,one may refer to(see[17],Lemma 3.1). ?

Lemma A.3Assume that kkL∞ ≤ 1 and p>1.Let g()be a smooth function ofwith bounded derivatives of any order,then for any integer m≥1,we have

ProofThe proof is similar to the proof of Lemma A.2 in[8]and is omitted here. ?