MIXED VARIATIONAL INEQUALITIES DRIVEN BY FRACTIONAL EVOLUTIONARY EQUATIONS∗

Stanis law MIGÓRSKI

College of Sciences,Beibu Gulf University,Qinzhou 535000,China;Chair of Optimization and Control,Jagiellonian University in Krakow,ul.Lojasiewicza 6,30348 Krakow,Poland E-mail:stanislaw.migorski@uj.edu.pl

Shengda ZENG(曾生达)†

Faculty of Mathematics and Computer Science,Jagiellonian University in Krakow,ul.Lojasiewicza 6,30348 Krakow,Poland E-mail:zengshengda@163.com;shengdazeng@gmail.com;shdzeng@hotmail.com

Abstract The goal of the present paper is to investigate an abstract system,called fractional di ff erential variational inequality,which consists of a mixed variational inequality combined with a fractional evolution equation in the framework of Banach spaces.Using discrete approximation approach,an existence theorem of solutions for the inequality is established under some suitable assumptions.

Key words fractional di ff erential variational inequality;C0-semigroup;Minty mixed variational inequality;existence;mild solutions

1 Introduction

Di ff erential variational inequalities(DVIs)were firstly systematically discussed by Pang-Stewart[21]in Euclidean spaces,because(DVIs)are useful to represent models involving both dynamics and constraints in the form of inequalities which arise in many applied problems,for example,mechanical impact problems,electrical circuits with ideal diodes,the Coulomb friction problems for contacting bodies,economical dynamics,dynamic traffic networks,and so on.After the work[21],more and more scholars are attracted to boost the development of theory and applications to(DVIs).For instance,Liu-Loi-Obukhovskii[15]studied the existence and global bifurcation problems for periodic solutions to a class of(DVIs)in finite dimensional spaces by employing the topological methods from the theory of multivalued maps and some versions of the method of guiding functions,Gwinner[3]obtained a stability result of a new class of(DVIs)by using the monotonicity method and the technique of the Mosco convergence,Chen-Wang[2]adopted the idea of(DVIs)to investigate a dynamic Nash equilibrium problem of multiple players with shared constraints and dynamic decision processes,and Ke-Loi-Obukhovskii[4]established the decay of solutions for a class of fractional(DVIs)in finite dimensional spaces via the theory of measures of noncompactness and a fixed point approach.

It is noteworthy that all aforementioned works were considered only in finite dimensional spaces.But,in our life,many applied problems in engineering,operations research,economical dynamics,and physical sciences,etc.,are more precisely described by partial di ff erential equations.Based on this motivation,recently,Liu-Zeng-Motreanu[9]and Liu-Migórski-Zeng[10]proved the existence of solutions for a class of(DVIs)in Banach spaces through applying the theory of semigroups,the Filippov implicit function lemma,and fixed point theorems for condensing set-valued operators.However,until now,fractional(DVIs)in in finite dimensional spaces were not investigated.To fill this gap,in this paper,we consider following fractional di ff erential variational inequality in Banach spaces

where the set SOL(K,g(t,x(t))+G(·),ϕ)stands for the solution set of the following mixed variational inequality: find u(t)∈K such that

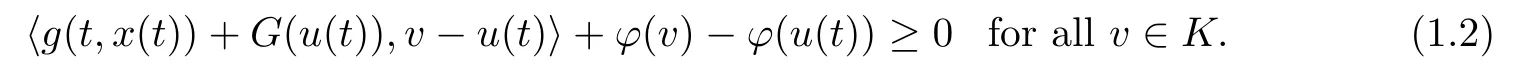
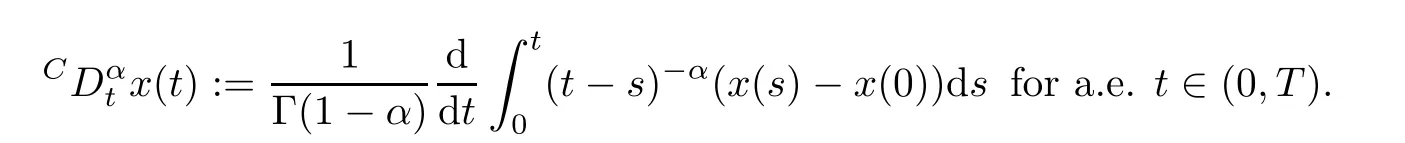
For more details on this topics the reader is welcome to consult[6–8,11–14,16,17,19,20,22,23,25–28]and the references therein.

According to our previous work[9,10]and Wang-Zhou[24],we give the de finition of solutions for problem(1.1)in the sense of mild.

De finition 1.1A pair of functions(x,u),with x∈C(0,T;X)and(0,T;K)for some β ∈ (0,α),is said to be a mild solution of problem(1.1),if

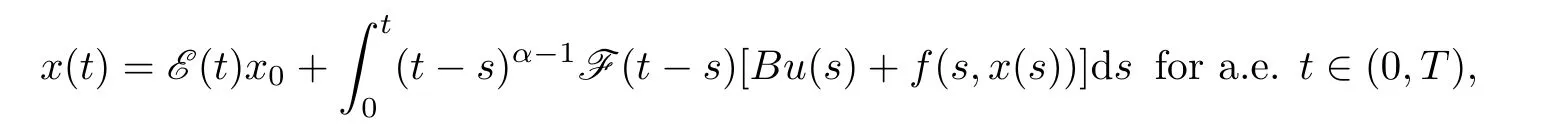
where u(t)∈ SOL(K,g(t,x(t))+G(·),ϕ)for a.e.t∈ (0,T),and

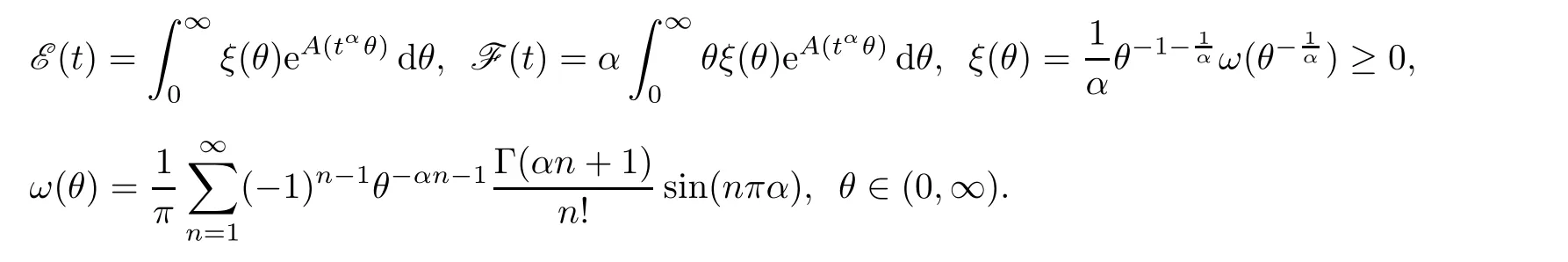
2 Main Results

Let E,X be real re flexive and separable Banach spaces,let K be nonempty,closed and convex subset of E.In what follows,the dual space of E is de fined by E∗.

Theorem 2.1(see[10,Theorem 3.2]) Assume that the following conditions are satis fied

A(G)G:E→E∗is monotone and hemicontinuous on K;

Then SOL(K,w+G(·),ϕ)is nonempty,bounded,closed and convex,for any w ∈ E∗.

Lemma 2.2(see[10,Lemma 3.1])Assume that A(G)and A(ϕ)hold.Then,u ∈SOL(K,w+G(·),ϕ)if and only if,it is also a solution of the following Minty mixed variational inequality problem: find u∈K such that

Proposition 2.3Assume that A(G)and A(ϕ)are ful filled.Then(x,u)∈ C(0,T;X)×L2(0,T;K)is a mild solution of problem(1.1)if and only if it solves the following system

for all v∈L2(0,T;K).

ProofLet(x,u)∈C(0,T;X)×L2(0,T;K)be a mild solution of problem(1.1).Then we have

From Lemma 2.2,we know that(2.2)is equivalent to

For any w∈L2(0,T;K),inserting v=w(t)into(2.3)and then integrating the inequality on(0,T),we conclude that(x,u)∈ C(0,T;X)×L2(0,T;K)is also a solution of problem(2.1).

Vice versa,we assume that(x,u)∈C(0,T;X)×L2(0,T;K)is a solution of problem(2.1).We now show that(x,u)∈C(0,T;X)×L2(0,T;K)solves problem(2.3).Arguing by contradiction,we suppose that there exist a measurable subset J⊂[0,T]with meas(J)>0 and v∗∈ K such that

Since u∈L2(0,T;K),so we may de fine the function w∈L2(0,T;K)by

Then,we take v=w∈L2(0,T;K)to inequality(2.1)to yield

This is a contradiction.Consequently,(x,u)∈C(0,T;X)×L2(0,T;K)solves(2.3)as well.Since(2.2)is equivalent to(2.3),so(x,u)∈C(0,T;X)×L2(0,T;K)is a mild solution of(1.1)too. ?

Finally,we show our main result.

Theorem 2.4Assume that A(G),A(ϕ),and the following conditions hold

A(g)g:(0,T)×X → E∗is a uniformly bounded function such thatis measurable on(0,T)for all x ∈ X,andis continuous for a.e.t∈ (0,T);

A(f)f:(0,T)×X → X is such thatis measurable on(0,T)for all x ∈ X and there exist β ∈ (0,α)andsuch that

If eAtis a compact C0-semigroup and B:E→X is a bounded linear operator,then problem(1.1)has at least one mild solution

ProofFor anyfixed,we consider the following fractional di ff erential equation

It follows from the assumptions and Wang-Zhou[24]that fractional di ff erential equation(2.4)has a unique mild solution

Let x be the unique mild solution of fractional di ff erential equation(2.4).Then,from[24,Lemma 2.9],we have

for all t∈[0,T],where c1>0 is independent of t,x and u.By the Gronwall inequality,we have

for all t∈[0,T],where c2>0 is independent of t,x and u.

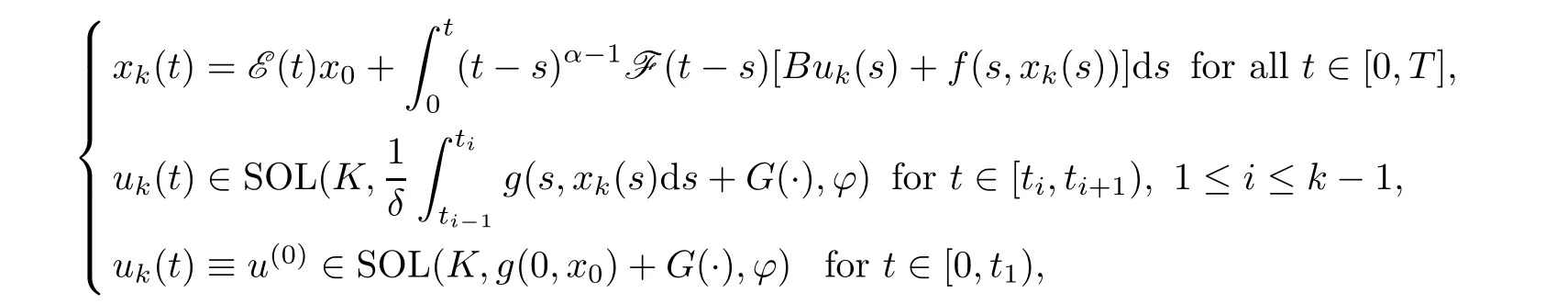
where ukis de fined by

in which χ[ti,ti+1)is the character function of interval[ti,ti+1).In this way,we can construct the sequences{uk}and{xk}.

For the sequence{uk},from hypothesis H(g)and[10,Theorem 3.3],we have kukkL∞(0,T;E)≤c3,where c3>0 is independent of k.However,estimate(2.7)indicates that kxkkC(0,T;X)≤c4,where c4>0 is independent of k.Without loss of generality,we may assume uk→u weakly in Lη(0,T;E),where η=max{2,}.Let x∈C(0,T;X)be the unique solution to problem(2.4)corresponding to u,i.e.,x satis fies equation(2.5).Then,we have

for all t∈[0,T],where c5>0 independent of k and t.Since,eAtis compact,then it is of course immediate from[5,Lemma 2.2]and the fact B(uk−u)→ 0 weakly in Lη(0,T;X),≤ β < α,that

Because hk(t)→0 in X as k→∞for all t∈[0,T].Invoking Gronwall inequality and Lebesgue-domainated convergence theorem,e.g.[18,Theorem 1.65],we conclude

thus

Consider the functional Φ:L2(0,T;K)→ R de fined by

We will show that Φ is a proper convex and lower semicontinuous functional.The property of Φ is obvious,because ϕ is proper.For w1,w2∈ L2(0,T;K)and λ ∈ (0,1),we have

so,Φ is convex.Let{wn}⊂L2(0,T;K)be such that wn→w in L2(0,T;K).Without loss of generality,we may assume that wn(t)→w(t)in K for a.e.t∈(0,T).On the other hand,from hypothesis H(ϕ),there exist r1,r2∈ R such that ϕ(v)≥ r1kvkE+r2for all v ∈ K.This deduces

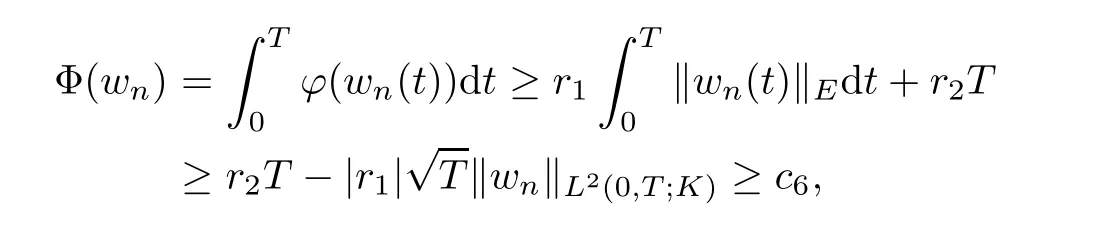
where c6∈ R is independent of n.The lower semicontinuity of ϕ and Fatou lemma indicate

This means that Φ is lower semicontinuous.

By de finition of ukand Lemma 2.2,we have

for a.e.t∈(0,T)and v(t)∈L2(0,T;K).

Since Lη(0,T;K)∋ uk→ u weakly in Lη(0,T;E),η≥ 2 and K is closed and convex,then we have u∈Lη(0,T;K)and uk→ u weakly in Lη(0,T;K)⊂ L2(0,T;K).This combined with weakly lower semicontinuity of Φ implies that

However the continuity of g and the convergence xk→x in C(0,T;X)ensures that

thus is Gk−G→ 0 in L2(0,T;E∗).However,from hypothesis H(g)and[1,Lemma 3.3],we have

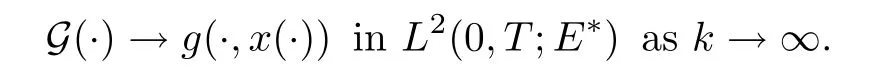
So,we have

Integrating(2.9)on(0,T),passing to the upper limit as k→∞,and then using convergences(2.10)–(2.11),we have

for all v∈L2(0,T;K).

Finally,we apply Proposition 2.3 to conclude thatis a mild solution of problem(1.1). ?

AcknowledgementsThis article is dedicated to one of Shengda Zeng’s best friend Ms.Yaping Qiu to the occasion of her honey wedding day(January 26,2018).