ZigZag微通道内S-CO2流动传热性能分析
2019-05-31
(合肥通用机械研究院有限公司,合肥 230031)
0 引言
印刷电路板式换热器(PCHE)由于其高效紧凑特性被广泛应用于海洋油气处理、浮式液化天然气装置以及核电领域[1-2]。超临界二氧化碳(S-CO2)流体因其物性表现出良好的流动传热性能而受到广泛关注[3]。目前,我国工业应用的PCHE大量依赖于进口,国内对其研究还相对滞后。故研究微通道换热器结构参数对流体流动传热性能影响意义重大,可为PCHE设计提供依据。
Dai等[4]利用粒子图像测速(PIV)技术对ZigZag半圆形横截面微通道内水的流动情况进行测试,发现雷诺数Re≈215时,水流动状态开始从层流转变至过渡态,并且观察到在流道弯曲位置附近产生回流旋涡,强化换热,并且该转捩点Re与流道粗糙度有关。Pra等[5]也认为弯曲微通道内弯曲位置附近流体流动产生的旋涡强化了换热。Kim等[6-8]对高温气冷反应堆用ZigZag半圆形横截面微通道内不同流体(氦-水、氦-氦、氦/二氧化碳-水)层流流动状态下传热特性进行了试验与数值模拟(采用周期流道模型),基于数值模拟结果拟合出不同工质局部努塞尔数Nu与阻力系数f关联式。Kim等[9]对文献[10]中试验用ZigZag半圆形横截面微通道(角度分别为32.4°与40°,冷热通道直径不相等)内超临界二氧化碳S-CO2(热侧入口280 ℃,3.2 MPa;冷侧入口108 ℃,10.5 MPa)在不同Re下的流动传热性能进行数值模拟,并对这两角度的ZigZag微通道内S-CO2的Nu与f关联式进行了拟合。Baik等[11]结合试验与数值模拟,对S-CO2布雷顿循环中PCHE进行研究,其中热工质S-CO2(压力7~9 MPa,温度25~45 ℃)处于湍流状态,冷工质水处于层流,并根据试验与模拟结果对文献[9]中的Nu与f关联式进行修正。李雪等[12-13]建立双通道模型对ZigZag半圆形横截面微通道内水在层流状态下的耦合传热特性进行研究,并拟合了Nu与f关联式。Karale等[14-20]采用第一/第二类边界,对PCHE单通道内流体流动传热性能进行了数值研究。
对于ZigZag流道型式的PCHE,研究对象均是基于试验模型,各关联式仅针对各自研究的工质、流动状态与相对应的结构参数,并且较多数值模拟研究是基于第一/第二类边界条件的单通道内流体流动传热性能研究。本文针对S-CO2布雷顿循环中低温回热器,以S-CO2流体为工质,建立三维双通道流固耦合模型,研究结构参数(ZigZag角度、单位周期流道轴向长度)对ZigZag半圆形横截面微通道内的流体流动传热性能影响。
1 ZigZag耦合传热数值模型
1.1 几何模型
本文研究的S-CO2布雷顿循环中低温回热器ZigZag板片流道结构见图1(a)。

(a)ZigZag板片
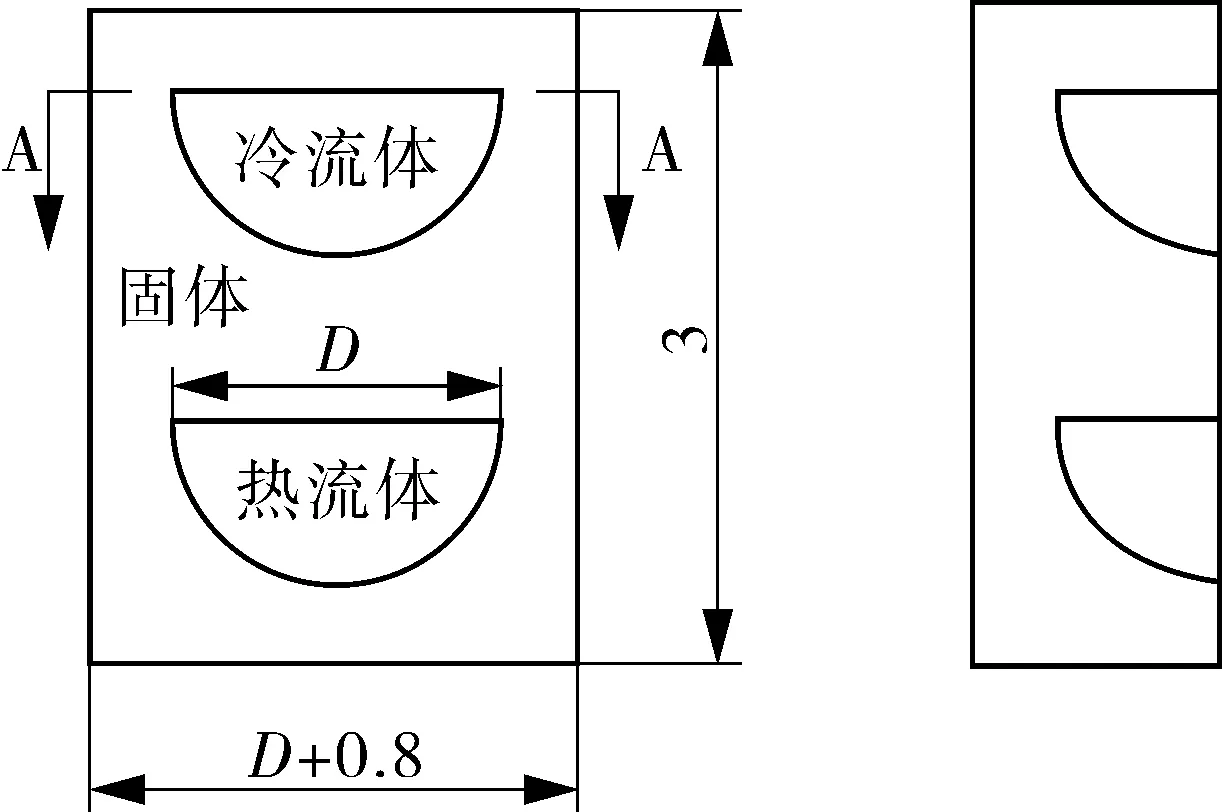
(b)双通道耦合传热计算几何模型与结构参数
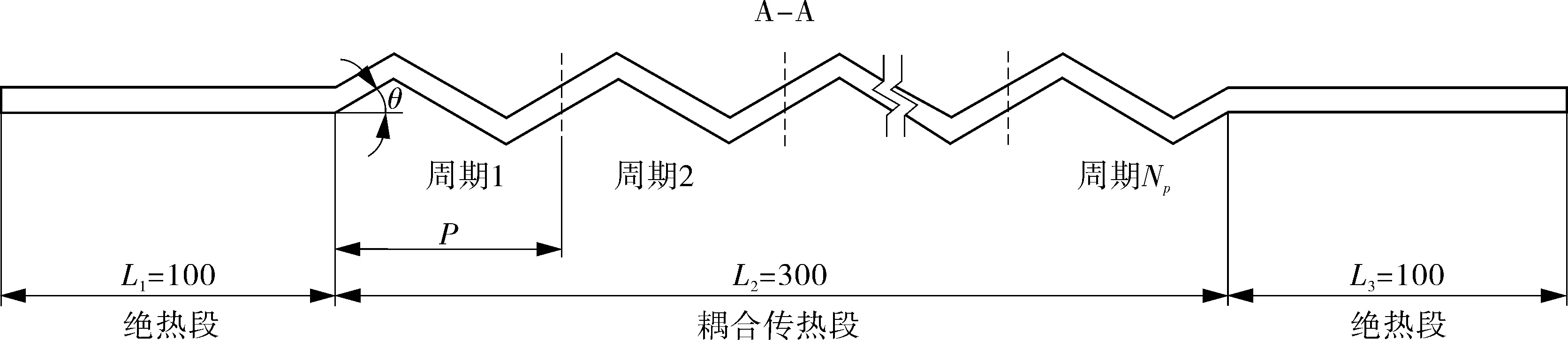
(c)ZigZag流道结构参数
该回热器是由多层板片堆叠而成,由于板片层数与每层板片上流道数量非常多,整体计算难以实现,根据其结构特点,建立冷、热工质双通道计算模型,其几何结构如图1(b),(c)所示,主要结构参数包括流道直径D(冷、热两侧相等)、ZigZag角度θ、单位周期流道轴向长度P、流道轴向长度L(进出口流道长度L1,L3与传热段流道轴向长度L2之和)。本文研究针对D=1.5 mm,P=10~30 mm,θ=0°~45°,Np=L2/P结构,为避免进口效应的影响,冷热流体在进出口各取长度100 mm直通道,在直通道内流体流动充分发展,再进入ZigZag通道进行耦合传热,由于流道对称,采用1/2对称模型计算。
1.2 数学模型及评价指标
流体流动与传热的连续方程、动量方程与能量方程可用以下通用形式表示[21]:
(1)
式中ρ——流体密度,kg/m3;
φ——通用变量;
u,v,w——流体沿x,y,z方向的流速,m/s;
Γ——广义扩散系数;
Sφ——广义源项。
努塞尔数Nu表征流道内流体传热性能,其值越大传热性能越好;阻力系数f表征流道内流体流动阻力,其值越小,流动阻力越小。综合传热增强因子PEC结合传热与流阻两方面,表征综合传热性能,其值大于1,说明综合传热性能优于基准通道(本文采用直径相同的半圆形横截面直通道作为基准),该值越大,综合传热性能越好。努塞尔数Nu、阻力系数f与综合传热增强因子PEC[22]计算如下:
(2)
(3)
(4)
1.3 求解设置
S-CO2作为工作介质,冷热流体逆流换热,假设流道内流体流动为稳态流动,计算时选择SSTk-ω湍流模型,边界条件设置如下:冷侧流体操作压力21.5 MPa,入口为速度入口,速度1.075 m/s,温度370.05 K,冷侧流体出口为压力出口;热侧流体操作压力8.2 MPa,入口为速度入口,速度10.72 m/s,温度597.95 K,热侧流体出口为压力出口;板片材料316L,进出口固体面为绝热面,各侧面为对称边界。
S-CO2的物性对温度极其敏感,其物性随温度变化较大,本文S-CO2物性来源于REFPROP,并将其拟合为以温度(360 K≤T≤600 K)为自变量的函数,再导入流体计算软件中进行计算。
1.4 网格无关性考核与数值模拟有效性验证
计算区域采用非结构化四面体网格,为消除网格对计算结果的影响,对其进行网格无关性考核。为提高壁面附近区域边界层内流体流动传热的精度,对流道传热壁面附近网格进行了局部加密,主体区域网格尺寸分别为0.2,0.15,0.1 mm。以模型θ=0°,L2=200 mm为例,采用3种网格尺寸(0.2,0.15,0.1 mm)计算,网格尺寸由0.2 mm减小至0.15 mm,冷热两侧出口温度变化分别为0.04%,0.03%,压降变化分别为1.583%,0.899%;网格尺寸由0.15 mm减小至0.1 mm,冷热两侧出口温度变化分别为0.006%,0.012%,压降变化分别为0.02%,0.648%。网格尺寸由0.15 mm细化至0.1 mm,出口温度与压降变化较小,故计算模型中网格尺寸取0.15 mm。
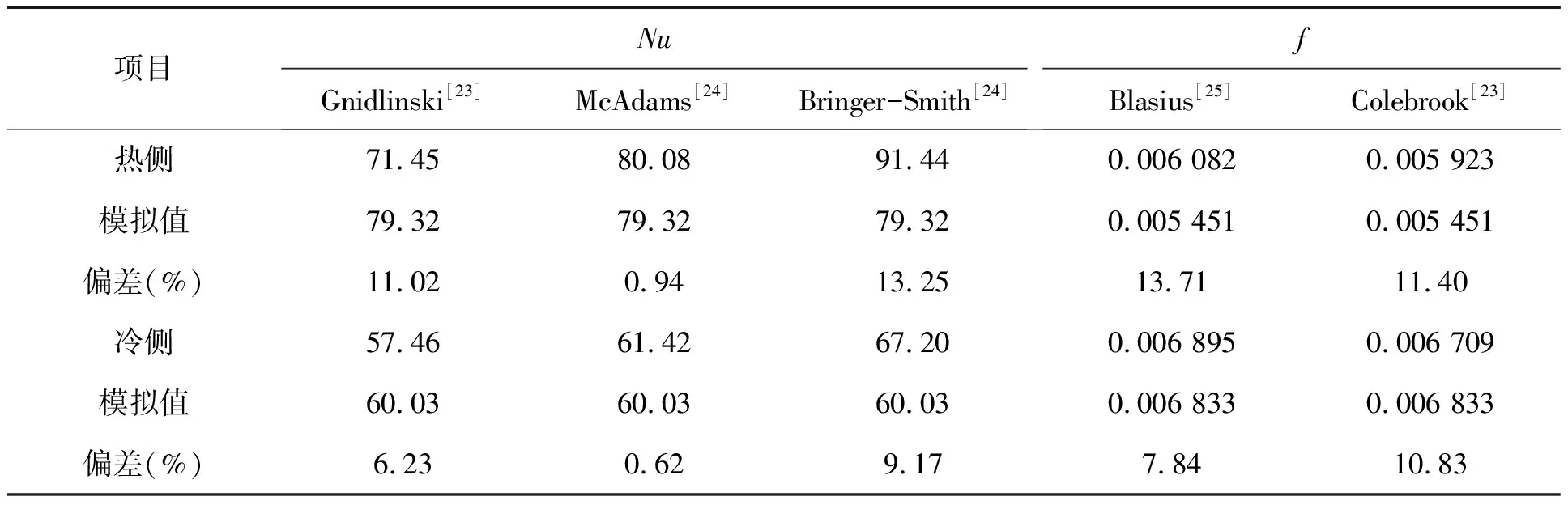
表1 数值模拟结果与关联式对比
由于目前现有的ZigZag微通道内S-CO2的Nu与f关联式较少,且本文研究的相关参数超出其适用范围,故利用直通道经验关联式验证数值计算模型的有效性。将直通道内数值计算Nu分别与Gnidlinski[23],McAdams[24],Bringer-Smith[24]关联式对比,f分别与Blasius[25],Colebrook[23]关联式对比,结果如表1所示。可以看出,Nu模拟值与对比关联式最大偏差为13.25%,f模拟值与对比关联式最大偏差为13.71%,各经验关联式均基于试验数据,该偏差在可接受范围内,故认为该数值模型是有效的。然后采用该数值模型对半圆形截面ZigZag微通道内S-CO2流动传热性能进行计算。
2 计算结果与分析
2.1 流动传热性能
以D=1.5 mm,P=20 mm,θ=40°,Np=1冷侧S-CO2流动传热情况为例,分析ZigZag微通道内传热流动性能。
2.1.1 流动性能分析
图2(a)为ZigZag通道与直通道内速度云图,图2(b)为流道局部流线图,图3为ZigZag通道与直通道内湍动能云图。由图2(a)可以看出,直通道内流体沿程流速稳定,而ZigZag通道内流体流速整体上高于直通道,在拐弯处速度大小变化剧烈;由图2(b)可以看出,直通道内流体流线与速度矢量均沿流道轴线方向,而ZigZag微通道内流道弯曲使流体流动方向改变,拐角内侧壁面的背风侧以及拐角外侧处有旋涡产生。旋涡产生使得流体流通面积减少,流道弯曲位置处流体主流速度急剧增大,且该股流体由于惯性冲刷换热壁面,使边界层减薄或破坏,强化传热。图3中直通道内壁面附近流体湍动能高于流道中心处流体,且沿流动方向上几乎保持不变,而ZigZag通道内流体湍动能高于直通道,并且在拐角内侧的背风侧S-CO2湍动能急剧增大,增强了流体的扰动与混合,促进流体间能量的传递。
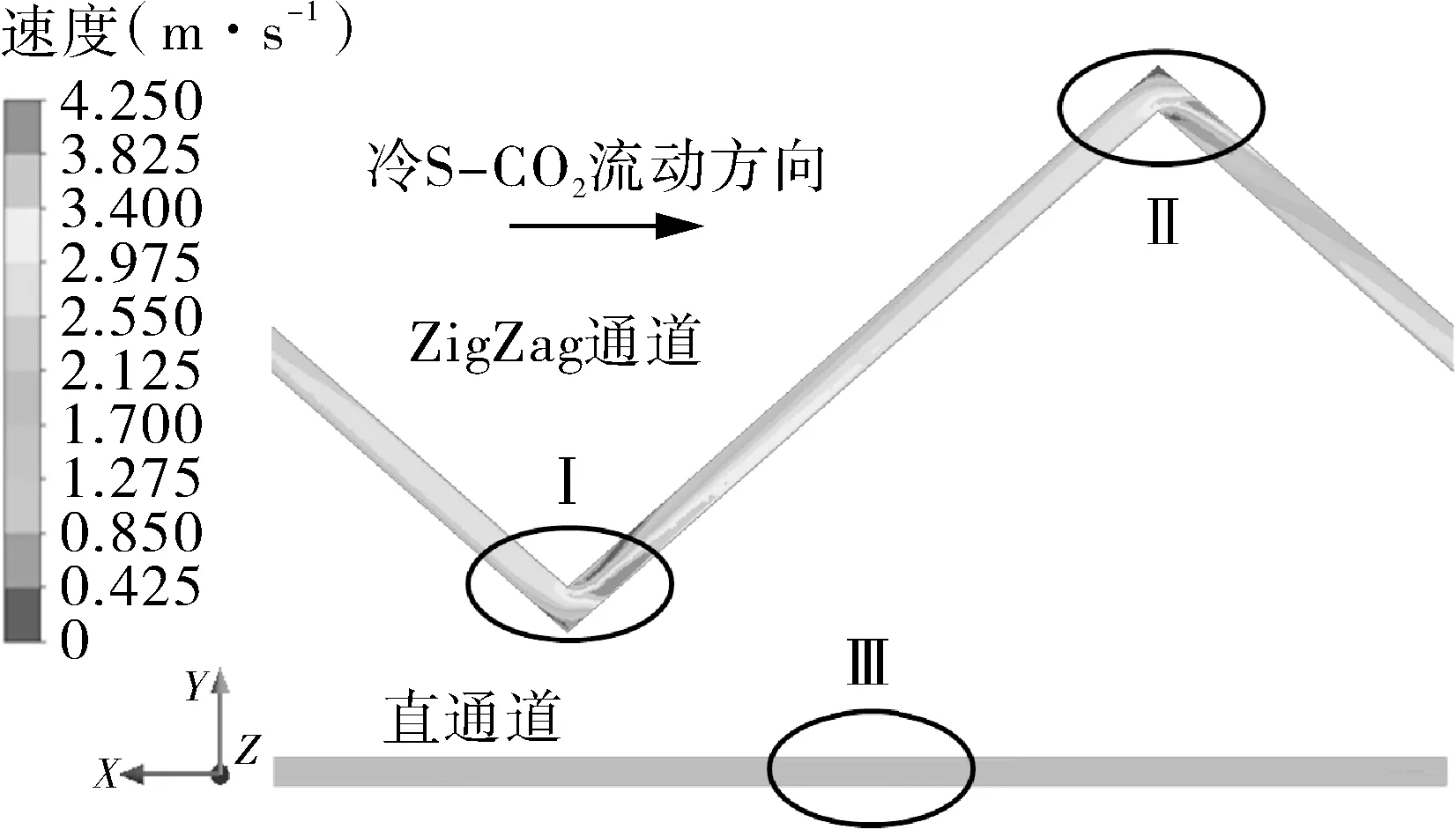
(a)微通道内流体速度变化情况
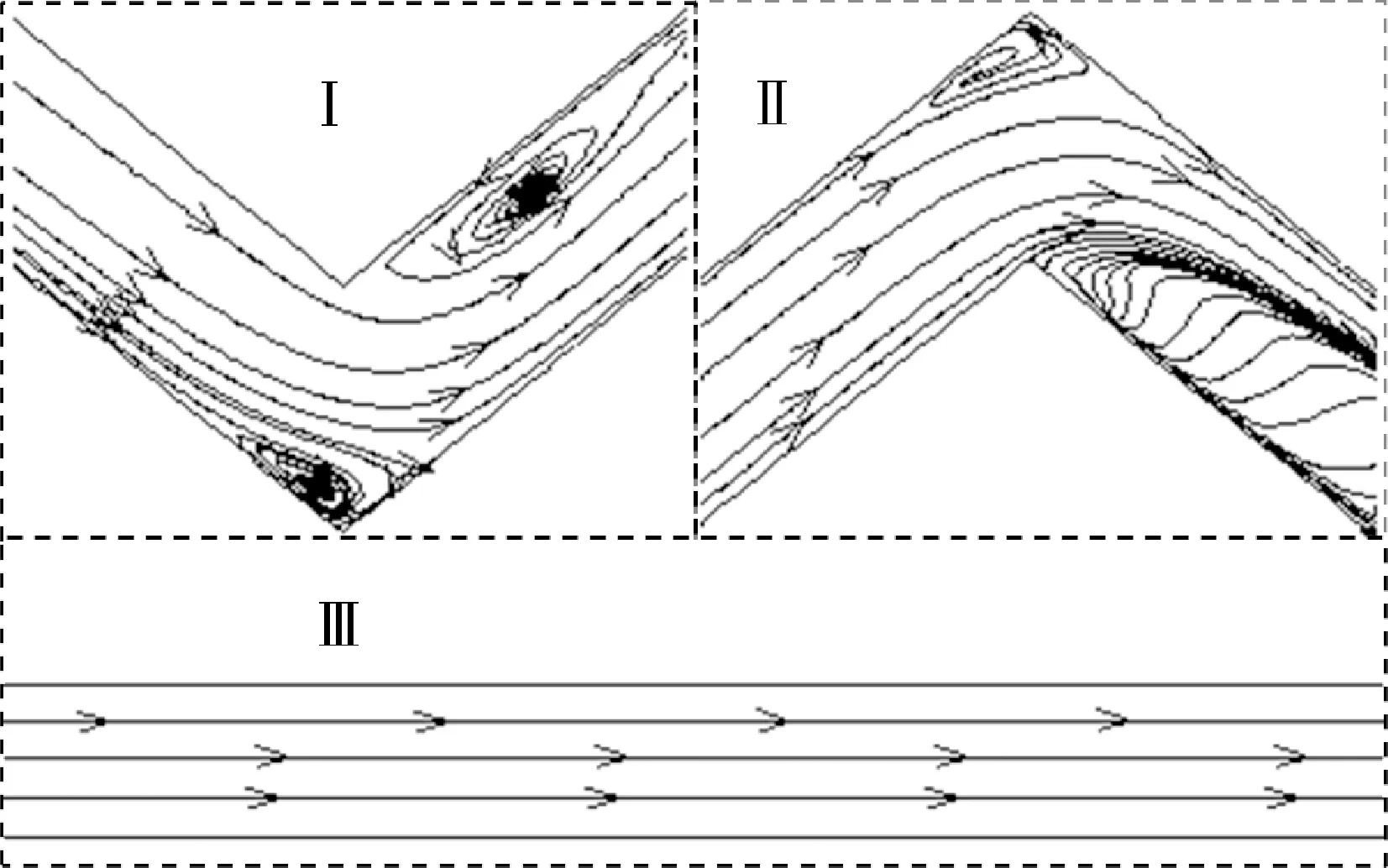
(b)微通道内局部位置流线
图2 ZigZag通道与直通道内流体流动情况对比
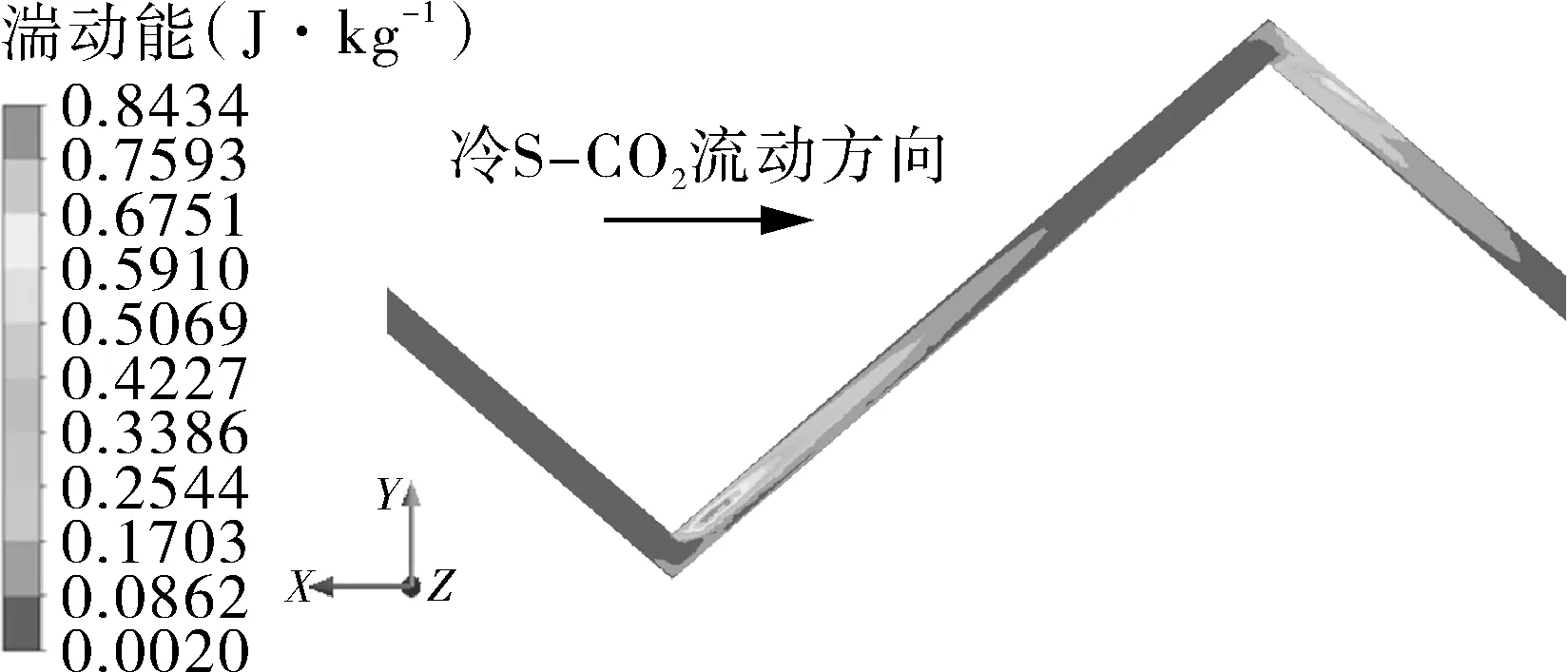
(a)ZigZag通道内湍动能变化情况
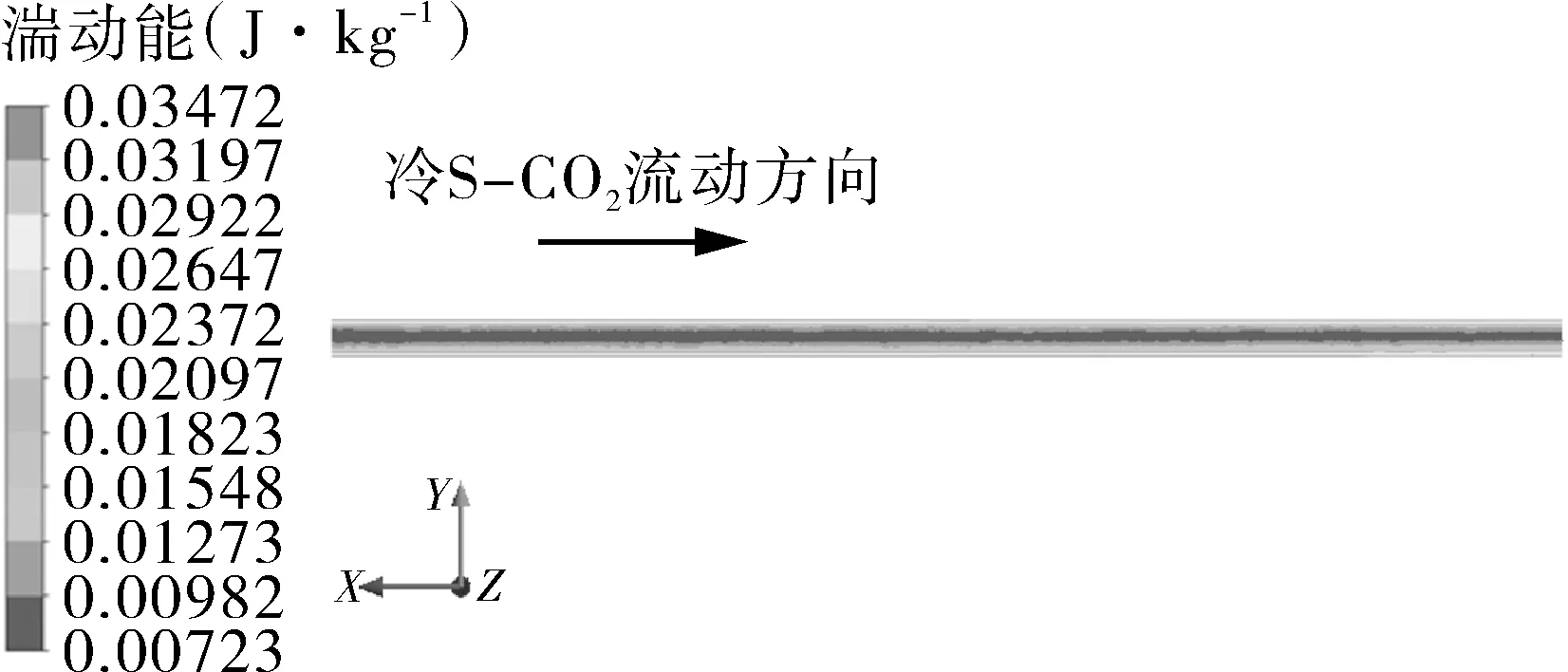
(b)直通道内湍动能变化情况
图3 微通道内流体湍动能变化情况
2.1.2 传热性能分析
图4(a)为流道内横截面分布位置,图4(b)为ZigZag通道与直通道各横截面温度分布云图。可以明显的看出,在相同的流动参数下,直通道壁面温度高于ZigZag通道,但经过一个周期后,ZigZag通道中心S-CO2温度明显高于相同轴向长度直通道内的流体温度,ZigZag通道壁面附近流体温度梯度明显比直通道小,在直通道内壁面附近流体温度梯度较大,即直通道内热边界层厚度明显比ZigZag通道大,也就是说ZigZag通道内S-CO2传热效果明显优于直通道。这是因为流道弯曲产生旋涡及流体冲刷壁面,使边界层减薄或破坏。从图4(b)可看出,相对于直通道,ZigZag通道n,q截面弧形壁面上边界层部分被破坏,o,p截面上壁面边界层减薄,壁面附近传热阻力减小,流道中心流体温度与壁面附近流体温度温差较小。
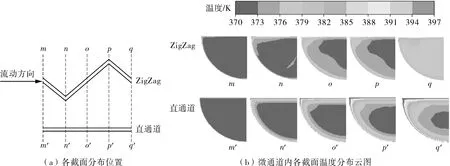
图4 微通道内各横截面温度分布情况
2.2 ZigZag角度θ对微通道内流体流动传热性能的影响
以D=1.5 mm,P=20 mm,θ=0°~45°几何结构为例,分析ZigZag角度θ对微通道内S-CO2流动传热性能的影响。
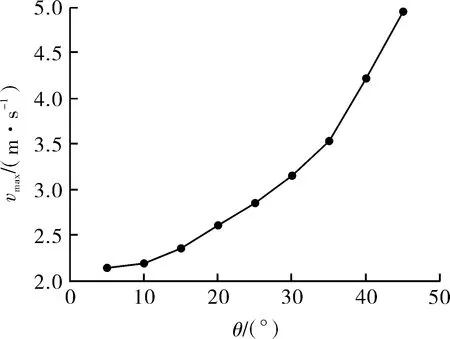
图5 流道内局部最大流速随角度θ变化曲线
各角度下ZigZag微通道(以D=1.5 mm,P=20 mm,Np=8冷流体通道为例)内局部流速最大值出现在流道弯曲位置附近,各角度下微通道内局部最大流速如图5所示。可以看出,随着ZigZag角度θ的增大,流道拐弯处局部流速显著增大,θ=5°时局部流速达到2.147 m/s;θ=30°时局部流速增大至3.157 m/s,与θ=5°时相比增大约1.5倍;θ=45°时局部流速高达4.957 m/s,与θ=5°时相比增大2.3倍,流道内局部流速增大,在流道弯曲位置对换热壁面附近边界层产生强烈冲刷,使边界层减薄或破坏,换热阻力减小,换热系数提高。
两侧S-CO2表面平均传热系数he与Nu随角度变化如图6所示。可以看出,0°≤θ≤45°范围内,两侧平均表面传热系数he与Nu变化趋势一致,均随ZigZag角度θ的增大而增大;ZigZag流道弯曲角度θ由0°提高至10°范围内,微通道换热性能提高,但其提高幅度较小;θ由10°提高至15°,微通道换热性能大幅度提升;θ由15°提高至25°范围内,微通道换热性能上升速率逐渐减小;θ由25°提高至45°范围内,微通道换热性能上升速率又迅速增大,即ZigZag微通道换热性能在10°~15°与30°~45°范围内提升较快。以直通道为基准,各角度下流道内传热性能(Nu/Nu0)如图7所示。在第1.3节所述计算条件下,ZigZag角度θ在5°~45°范围内,热侧微通道内S-CO2传热性能提高0.6%~87.4%,冷侧微通道内S-CO2传热性能提高1.4%~100.3%。
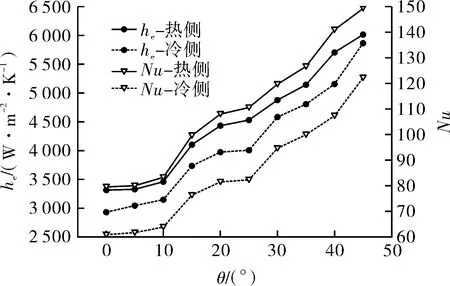
图6 平均表面换热系数he与Nu随角度θ变化曲线
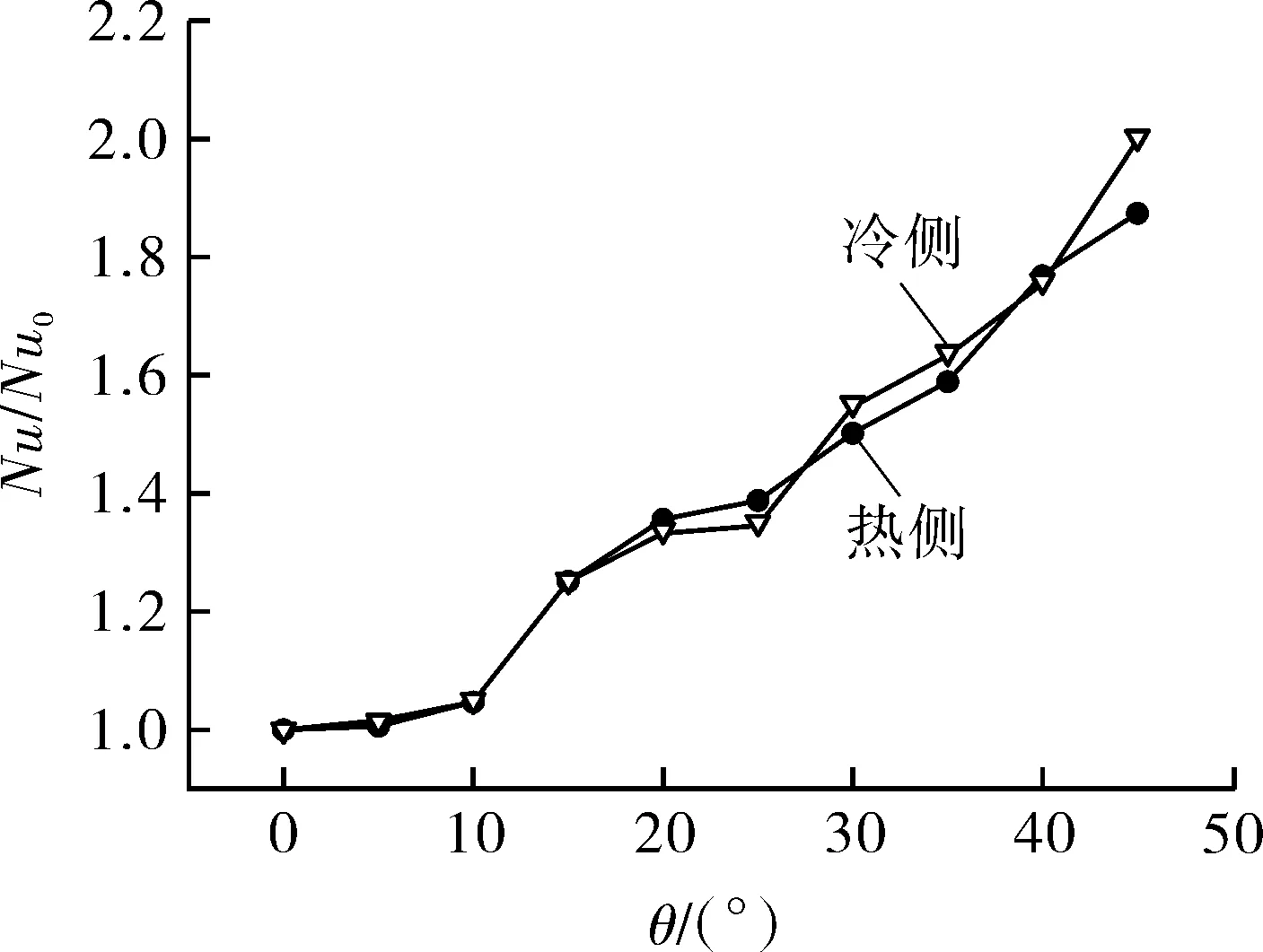
图7 S-CO2传热性能随角度θ变化曲线
各角度下流道内流动阻力系数如图8所示。可以看出,流动阻力系数f随角度θ的增大而增大;流道角度从0°增大至25°,流体流动阻力增加相对缓慢;流道角度从25°继续增大至45°时,流体流动阻力迅速增大。图8中冷流体流道内流动阻力系数均高于热流体流道,这是流体物性导致的。以直通道为基准,各角度下微通道内阻力性能(f/f0)见图9。在第1.3节所述计算条件下,ZigZag角度θ在5°~45°范围内,热侧微通道内S-CO2流动阻力系数最大增大约12倍,冷侧微通道内S-CO2流动阻力系数最大增大约9.5倍。
微通道内S-CO2传热性能与流动阻力均随ZigZag角度θ(5°~45°)的增大而升高,为了说明流道的流动传热性能,利用综合传热增强因子PEC来分析流道的综合传热性能。图10示出各角度下ZigZag微通道内S-CO2耦合传热两侧流体的综合传热增强因子PEC变化情况,图中θ=5°,15°,20°时,两侧ZigZag微通道PEC值均大于1,即微通道内流体综合传热性能优于直通道,θ在25°~45°范围内以及θ=10°时,ZigZag流道PEC值均小于1,虽然Nu随θ增大而增大,但f随θ增长得更快。 在P=20 mm,θ为5°~45°范围内,θ=15°时,ZigZag微通道内两侧流体综合换热性能最优,热侧综合换热性能提高5%,冷侧综合换热性能提高8%。
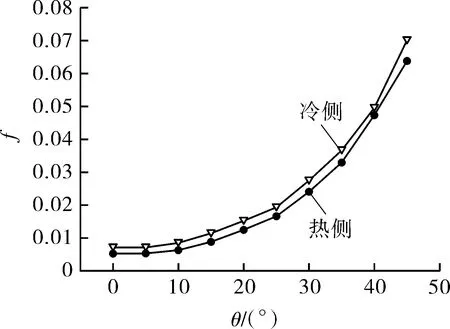
图8 S-CO2流动阻力系数f随角度θ变化曲线
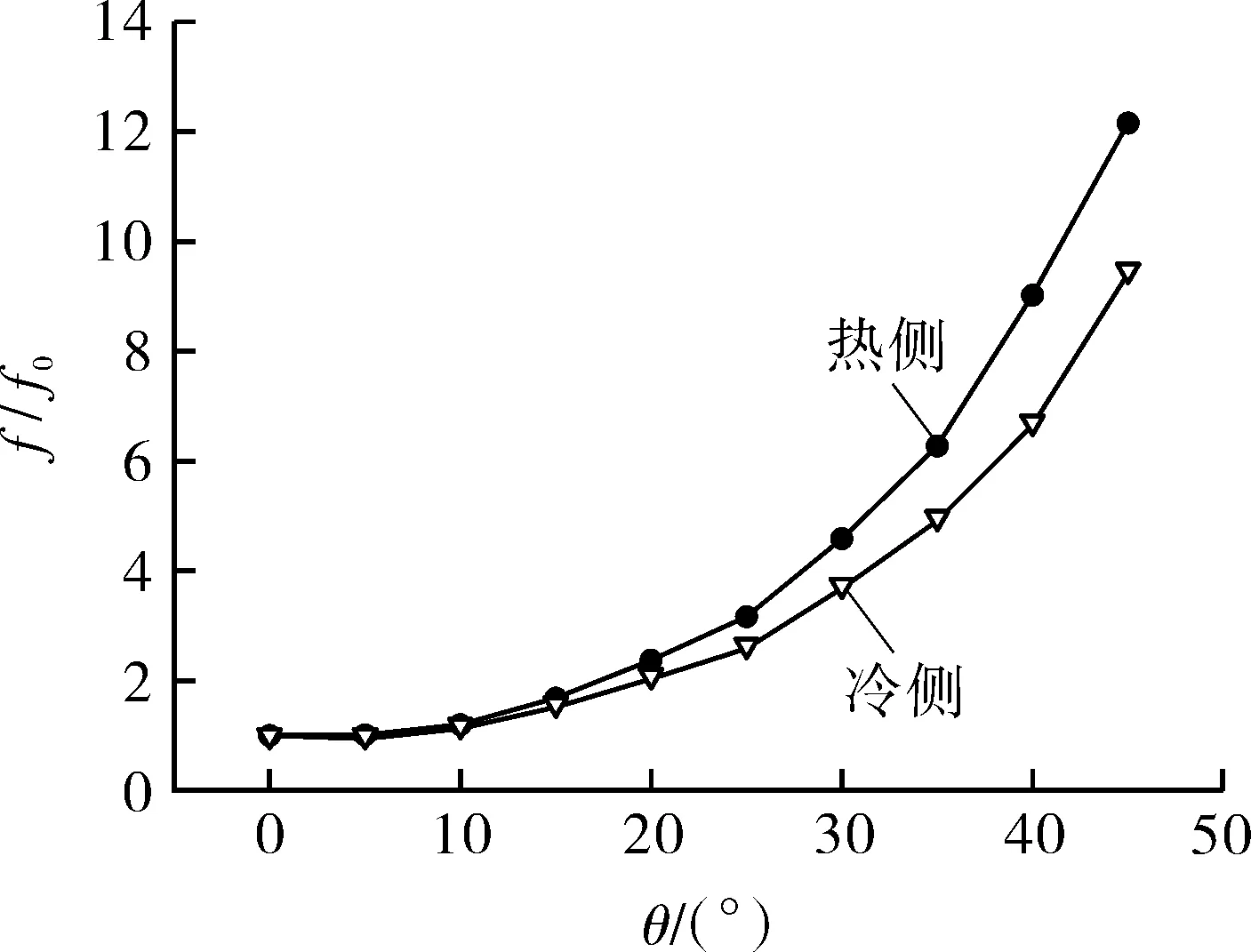
图9 S-CO2阻力性能随角度θ变化曲线
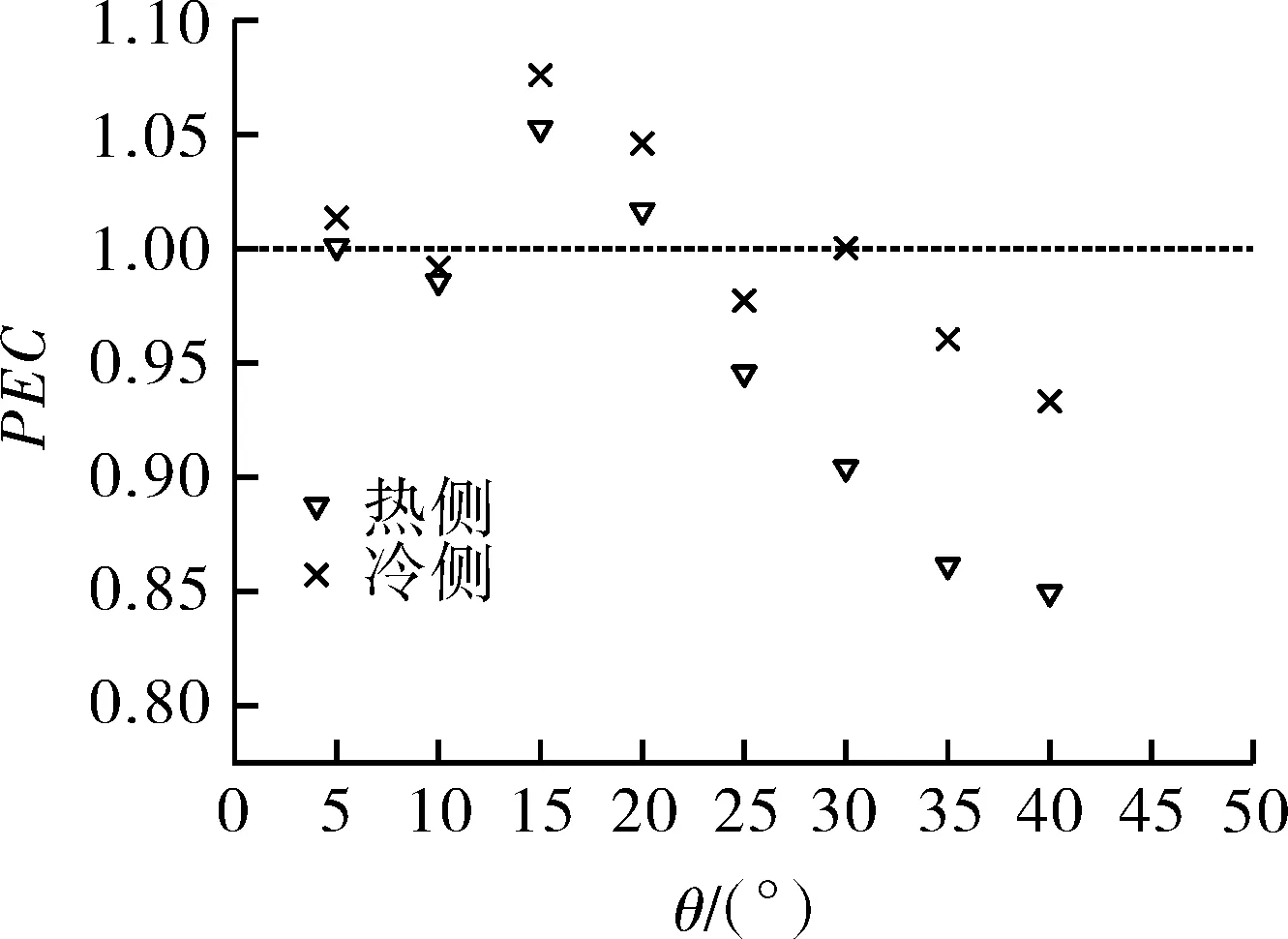
图10 S-CO2综合传热性能随角度θ的变化
2.3 单位周期流道轴向长度P对微通道内S-CO2流动传热性能的影响
以D=1.5 mm,θ=15°,P=10~30 mm几何结构为例,分析单位周期流道轴向长度P对微通道内S-CO2流动传热性能的影响。
两侧S-CO2表面平均传热系数he与Nu随长度P变化见图11。可以看出,P=10~30 mm范围内,he与Nu变化趋势相似,均随长度P的增大而减小;he随P的增大平缓下降,而P从10 mm增大至15 mm,从20 mm增大至30 mm,Nu缓慢下降,而P从15 mm增大至20 mm,Nu急速下降。以直通道为基准,各长度P下流道内S-CO2传热性能(Nu/Nu0)见图12。在第1.3节所述计算条件下,ZigZag长度P在30~10 mm范围内,热侧微通道内S-CO2传热性能提高22.2%~31.2%,冷侧微通道内S-CO2传热性能提高24.7%~37%。
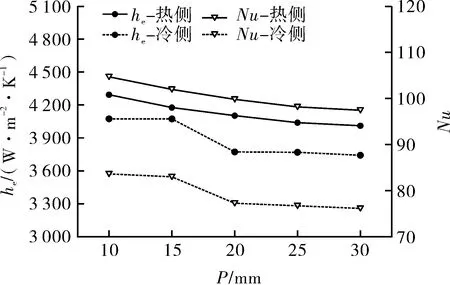
图11 平均表面换热系数he与Nu随长度P变化曲线
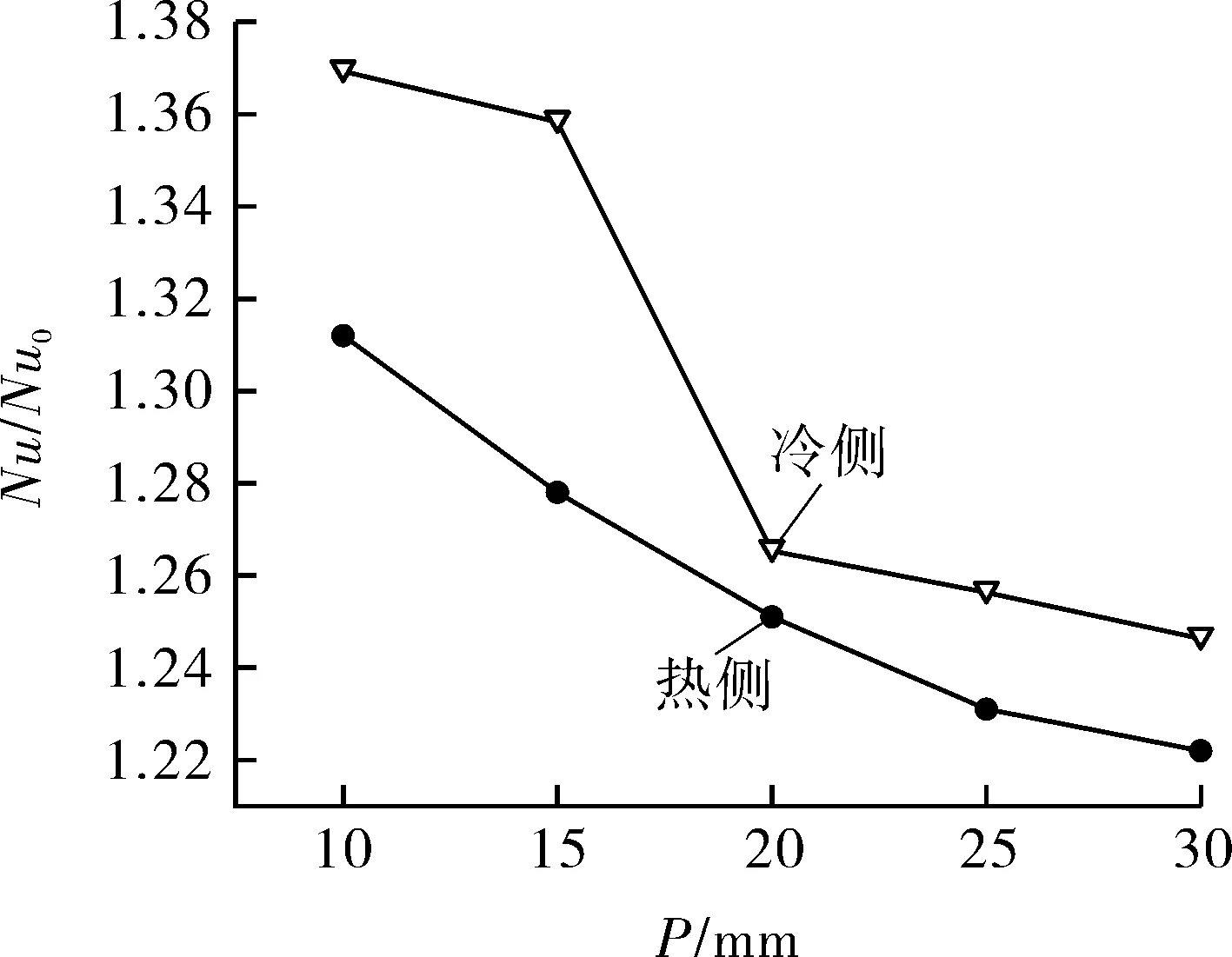
图12 S-CO2传热性能随长度P变化曲线
各长度P下流道流动阻力系数f见图13。可以看出,f随长度P的增大而减小。图中冷流体流道内流动阻力系数均高于热流体流道,这是流体物性导致的。以直通道为基准,各长度P下阻力性能见图14。在第1.3节所述计算条件下,θ=15°时,ZigZag长度P在10~30 mm范围内,在P=10 mm时阻力系数最大;与直通道相比,热侧微通道内S-CO2阻力系数最大增大约1倍,冷侧微通道内S-CO2阻力系数最大增大约0.9倍。
图15示出ZigZag角度θ=15°时不同长度P(10~30 mm)下微通道内S-CO2耦合传热两侧流体的综合传热性能增强因子PEC变化情况。以直通道为基准,在计算范围内,ZigZag微通道流动传热性能优于直通道,热侧S-CO2微通道内综合传热性能提高3.5%~6%,在P=25 mm时最优;冷侧S-CO2微通道内综合传热性能提高7%~11%,在P=15 mm时最优。综上所述,在第1.3节所述计算条件下,兼顾冷热两侧S-CO2,D=1.5 mm,θ=15°,P=15 mm时,ZigZag微通道内S-CO2耦合传热综合传热性能最优。
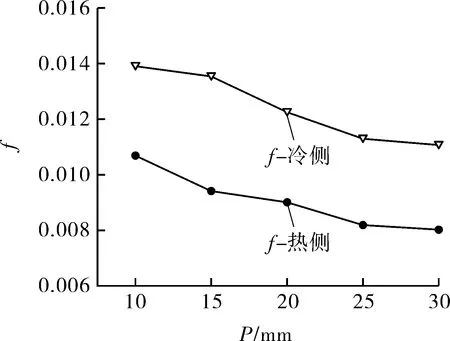
图13 S-CO2流动阻力系数f随长度P变化曲线
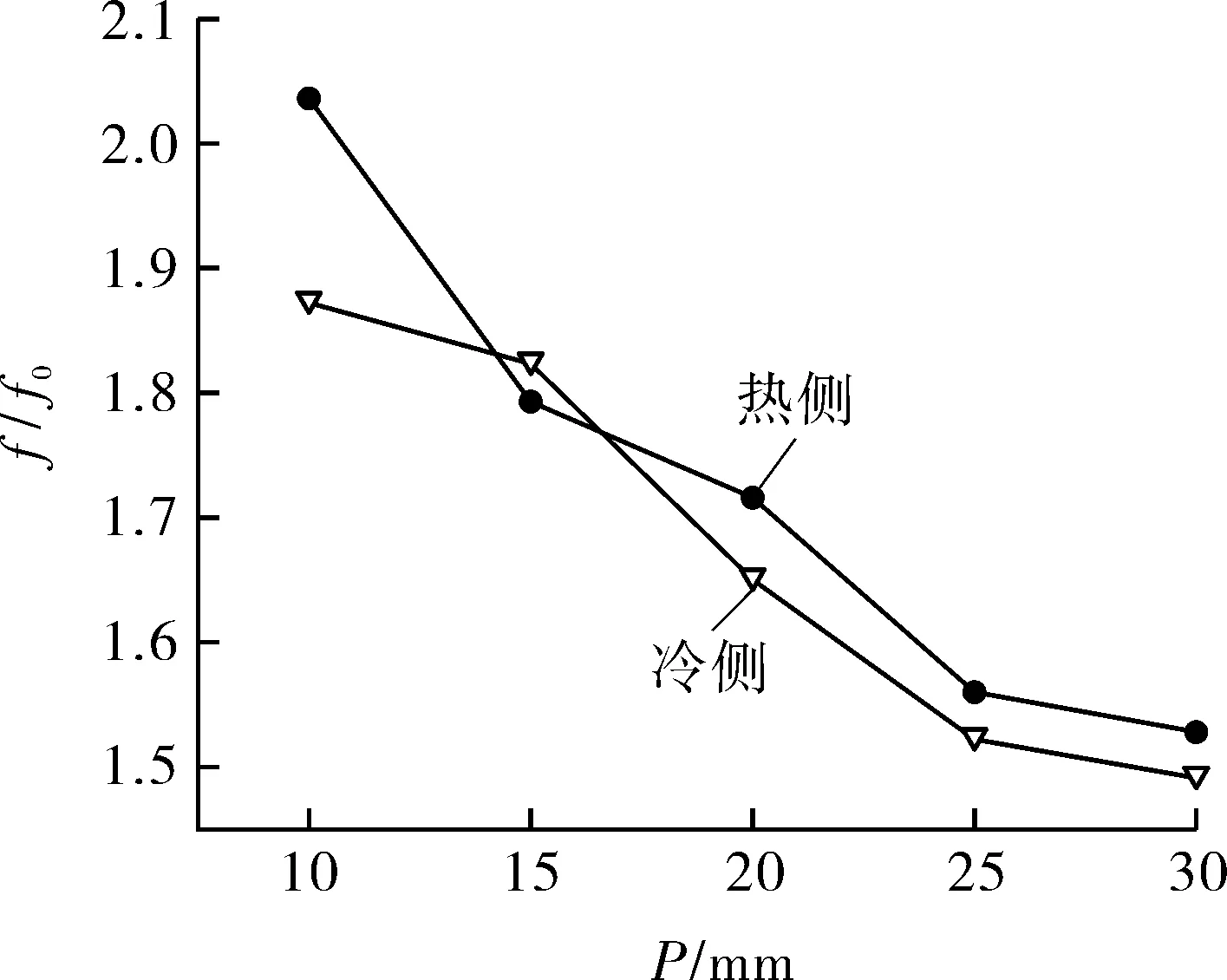
图14 S-CO2阻力性能随长度P变化曲线
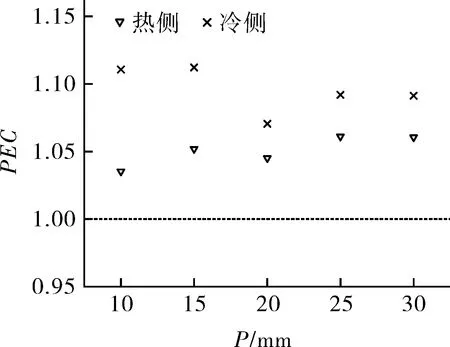
图15 S-CO2综合传热性能随长度P的变化
3 结论
本文对ZigZag微通道内S-CO2湍流状态下的流动传热性能进行了数值模拟,得到结论如下。
(1)流体在ZigZag微通道内流动,在流道拐弯处有旋涡产生,导致流道流通面积减少,流体主流速度急剧增大并冲刷换热壁面,使边界层减薄或破坏,并且该附近位置湍动能急剧增大,增强流体的扰动与混合,促进能量传递,强化换热。
(2)随着ZigZag角度θ的增大,微通道内S-CO2传热性能提高而流动阻力急剧增大;随着单位周期流道轴向长度P的增大,传热性能与流动阻力均下降;在文中所述计算条件下,θ=15°,P=15 mm时,ZigZag微通道内S-CO2耦合传热综合传热性能最优。
