无级变速器减压回路压力脉动关键参数识别及优化验证
2019-05-31周云山瞿道海张飞铁胡哓岚
罗 威 周云山,2 瞿道海 张飞铁 胡哓岚
1.湖南大学汽车车身先进设计制造国家重点实验室,长沙,410012 2.湖南容大智能变速器股份有限公司,长沙,410205
0 引言
2017年全球乘用车市场销量接近9 000万辆,其中自动变速器占比接近50%。随着国内自动变速器市场不断增长,金属带式无级变速器(continuously variable transmission,CVT)由于其结构简单、挡位无级化、成本相对较低的优点,在国内拥有巨大的市场需求。同时市场也在不断促进CVT技术升级换代,目前独立液压系统的研发已引起行业的重视。在独立液压回路设计中,CVT主动、被动油缸压力通过主动、被动两条减压回路来进行控制。相比其他类型自动变速器,CVT通过金属带的摩擦传动来实现动力传递,在主动、被动油压发生波动,尤其是低频率大幅度压力脉动时,金属带极易发生打滑,造成变速器不可逆的加速失效。因此对金属带实时夹紧力即主被动油压稳定地进行控制关系到CVT变速箱的使用寿命及维护成本。
CVT所用的液压泵源基本为齿轮泵或叶片泵,此类泵在结构原理上是容积式的非连续性吸油排油,会无法避免地产生流量脉动,再加上客户实时操控需求,造成各液压执行机构实时的不同流量需求及压力需求,从而对各执行机构压力稳定性控制带来了挑战。
为解决压力脉动问题,杨华勇等[1]、MA等[2]、GAO等[3]从液压系统泵源的角度研究减小流量脉动的方法,曹树平等[4]从自适应蓄能器的角度、欧阳小平等[5]从脉动衰减器的角度来提高压力的稳定性,冀宏等[6]、YE等[7]对滑阀节流槽进行了分析,王关海等[8]从电磁供油定值减压阀的角度进行了分析。以上都是从单个液压元件的角度分析来减少压力脉动,没有基于执行器负载流量需求来考虑复杂液压系统,如没有综合考虑减压滑阀、滑阀节流槽、先导阻尼孔、反馈阻尼孔、弹簧、蓄能器等来分析压力脉动衰减的关键参数。因此如何从系统的角度来分析压力脉动,识别出关键影响因素十分重要。
试验设计(design of experiment, DoE)是识别系统关键参数的重要手段,是提高产品质量、优化工艺流程的重要方法。传统的DoE方法如中心组合法、正交试验法在低维变量少样本时作用较大,但涉及到多变量大样本量时,其低效的缺点显露无疑。而且传统试验需要加工各极限样件,周期长、成本高昂,不利于产品的快速开发。因此在设计及故障优化过程中,急需一种有效方法来快速识别出系统关键参数。
Sobol’[9]在上世纪90年代初提出了灵敏度分析方法,该方法以方差为基础来进行参数识别,经不断发展[10-15]及应用[16-18]已经成为非常经典的灵敏度分析算法。本文以CVT主动比例减压回路为分析实例,基于执行器负载流量需求(等效负载阻尼孔),在AMESim中建立含先导端蓄能器、先导阻尼孔、反馈阻尼孔、带节流槽的减压滑阀的液压模型,引入Sobol’的全局灵敏度分析方法,分析不同频率压力激励下减压回路的滤波特性,识别出脉动幅值衰减灵敏度参数,提高减压回路的稳定性设计;然后根据灵敏度分析结果,结合实车主动压力脉动故障现象,再运用响应曲面的方法,优化主动减压回路设计参数;最后根据优化结果进行试验验证。
1 减压回路液压模型
由于乘用车几何空间及成本要求,CVT液压系统各控制滑阀为自主(非标)设计,为体现各液压阀连接通口数、工作位置及机能,参考文献[19]绘制了CVT液压原理示意简图(图1)。

1.油泵 2.流量阀 3.一级溢流滑阀 4.二级溢流滑阀 5.三级溢流滑阀 6.去冷却润滑 7.液力变矩器(TC)8.倒挡油缸 9.前进挡油缸 10.手动换向阀 11.减压兼换向滑阀 12.比例溢流阀 13.二级定值减压阀14,16,17,18.比例减压阀 15.蓄能器 19.一级定值减压阀20,21.减压滑阀 22.主动油缸 23.被动油缸图1 CVT独立液压回路原理示意图Fig.1 Simplified configuration of a independenthydraulic actuation system of CVT
图1中,主动油缸22压力由减压滑阀21控制,被动油缸23压力由减压滑阀20控制,二者压力控制相互独立,故称为独立液压回路(独立液压系统);比例减压阀16、17、18作为先导电磁阀,通过分别控制一级溢流滑阀3、减压滑阀21、20来实现系统压力、主动压力、被动压力的调节;比例减压阀16直接控制CVT离合器压力,通过手动换向阀10的切换通向倒挡油缸8或者前进挡油缸9;比例溢流阀12作为先导电磁阀通过控制二级溢流滑阀4、减压兼换向滑阀11来实现系统二级压力和液力变矩器7的压力调节。
由图1可知,整个液压系统稳定性分析模型涉及多自由度多阶振动的非线性模型,并且模型间各液压回路的耦合性较强,参数的非线性及不确定性较多,利用传统方法识别系统的压力稳定性关键参数较为困难。
图1中阀11、13、19、20、21皆为减压滑阀,因此单独进行减压回路稳定性分析对CVT液压系统设计具有极为重要的意义。
典型减压回路如图2所示。图2中主动减压
回路由主动减压滑阀、滑阀弹簧、先导阻尼孔和反馈阻尼孔、弹簧式蓄能器及先导比例电磁阀组成。其前端供给压力由图1中一级溢流阀3控制,滑阀减压后输出至主动带轮油缸。由于先导比例电磁阀固有频率为127 Hz,对主动滑阀的影响较小,故本文将先导阀作为比例环节处理。
1.1 负载流量模型
主动、被动减压回路所控制的CVT带轮简
图及关键参数如图3所示。CVT速比计算公式如下:
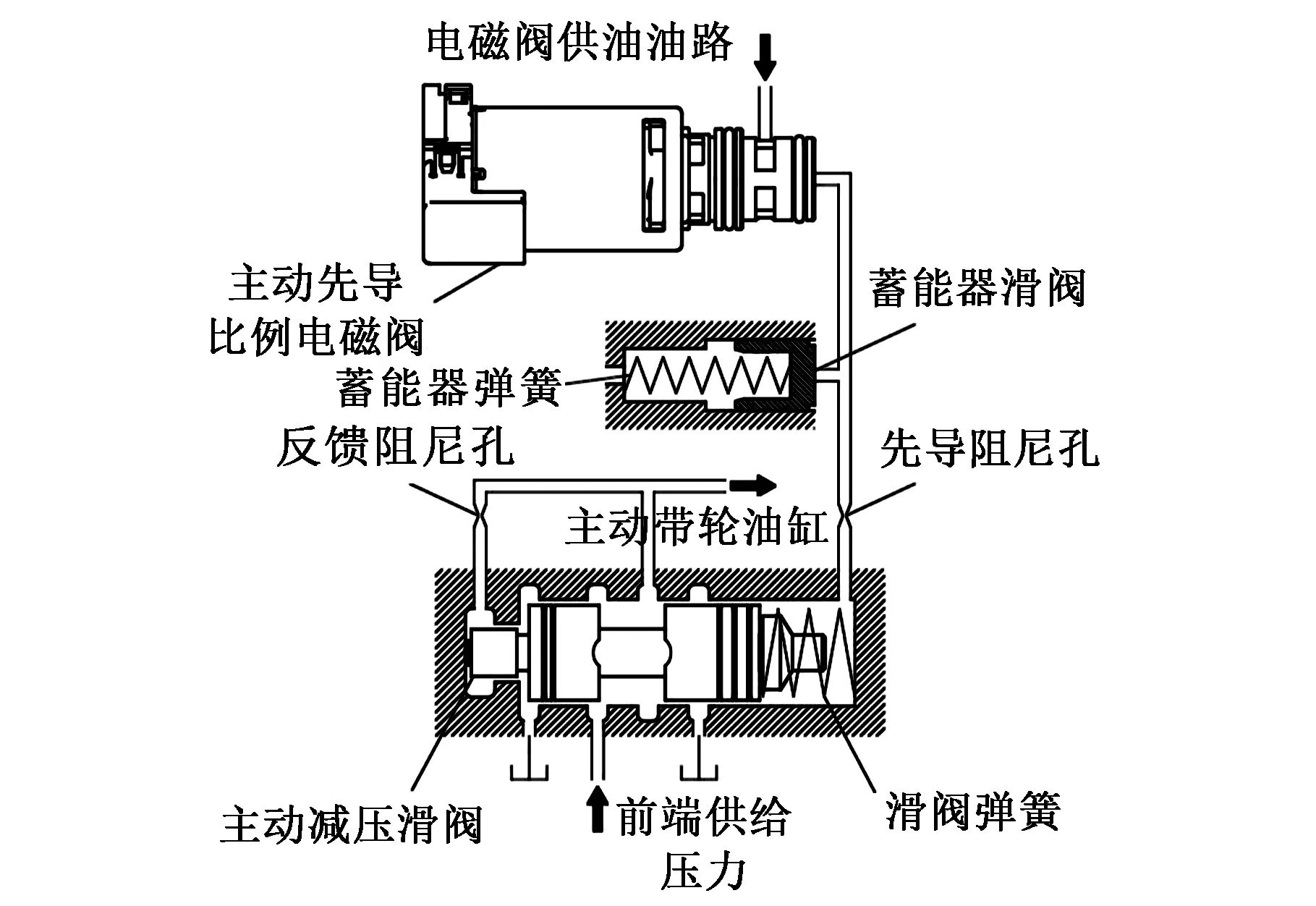
图2 主动减压回路示意图Fig.2 Primary pressure reduction circuit

图3 带轮简图Fig.3 Schematic overview of a pushbelt variator
Q?st=Q?sr+Q?slQ?pt=Q?pr+Q?pl
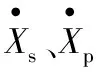
移变化率(轴向速度);Q?sr、Q?pr为被动、主动油缸变速需求流量;A?s、A?p为被动、主动带轮油缸活塞面积;Q?sl、Q?pl为被动、主动减压回路泄漏量;Q?st、Q?pt为被动、主动减压回路总负载流量。
在整车实际驾驶过程中,主动、被动减压回路所需负载流量主要为回路泄漏流量及变速流量。如果金属带轮传动速比未变,则主动、被动减压回路的流量需求为各带轮及其减压回路的泄漏量Qpl、Qsl,在变速时还要考虑速比变化带来的油缸流量的变化Qpr、Qsr。其中主动、被动减压回路泄漏量为试验测试所得,测试结果如图4所示。

图4 主动、被动减压回路泄漏量(90 ℃)Fig.4 Leakage flow of primary & secondaryreduction circuits(90 ℃)
对于主动减压回路,其负载流量等效阻尼孔直径D?L与主动总负载流量Q?pt关系如下:
(1)
其中,C?q为流量系数;Δp?为阻尼孔前后压差;ρ?为CVT油密度。由式(1)可知,根据主动变速流量Q?pr及减压回路的泄漏量Q?pl即可推导负载流量等效阻尼孔直径D?L。
1.2 蓄能器液压模型
蓄能器为弹簧式蓄能器,模型如图5所示。其动力学方程如下:
(2)
其中,p?pilot为比例电磁阀输出的先导压力;K?a为蓄能器弹簧刚度;X?a为蓄能器滑阀位移;D?a为蓄能器滑阀直径。式(2)表示蓄能器弹簧预紧力为0。
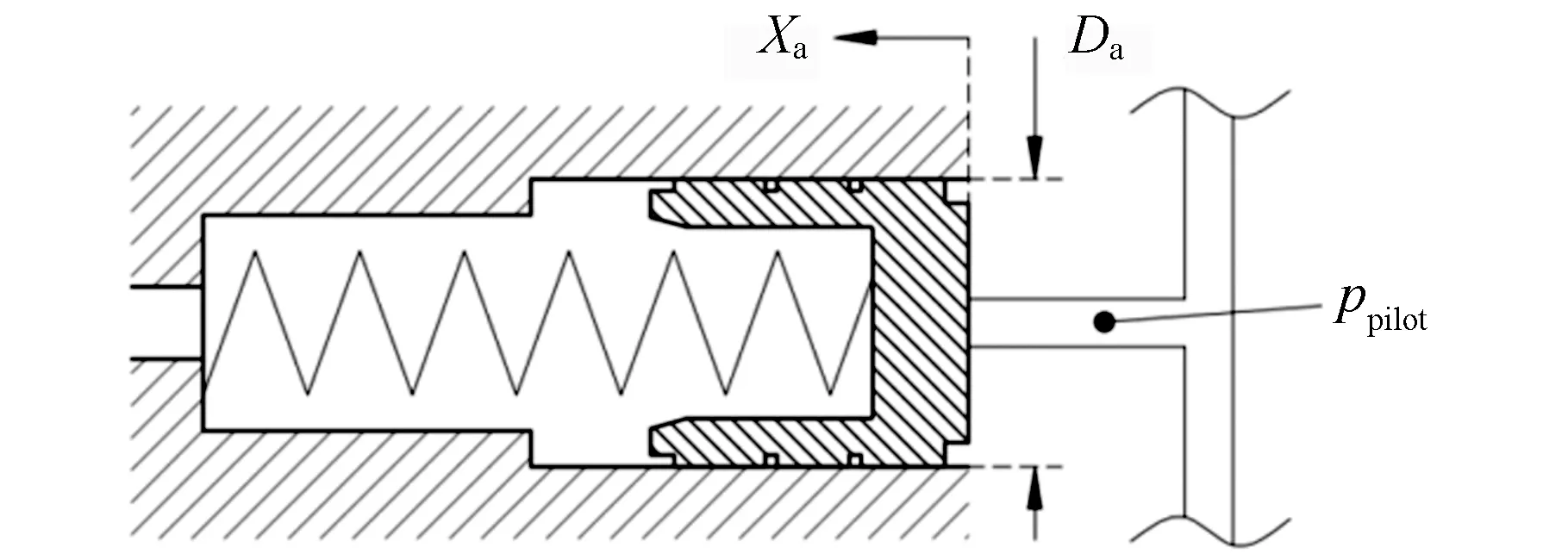
图5 蓄能器示意图Fig.5 Schematic overview of spring accumulator
1.3 主动减压滑阀液压模型
本文滑阀模型采用非全周口节流边,根据加工和检验工艺性要求,并且为避免文献[7]出现的二次节流现象,在节流边上采用对开的2个平底圆形槽。具体参数见图6。
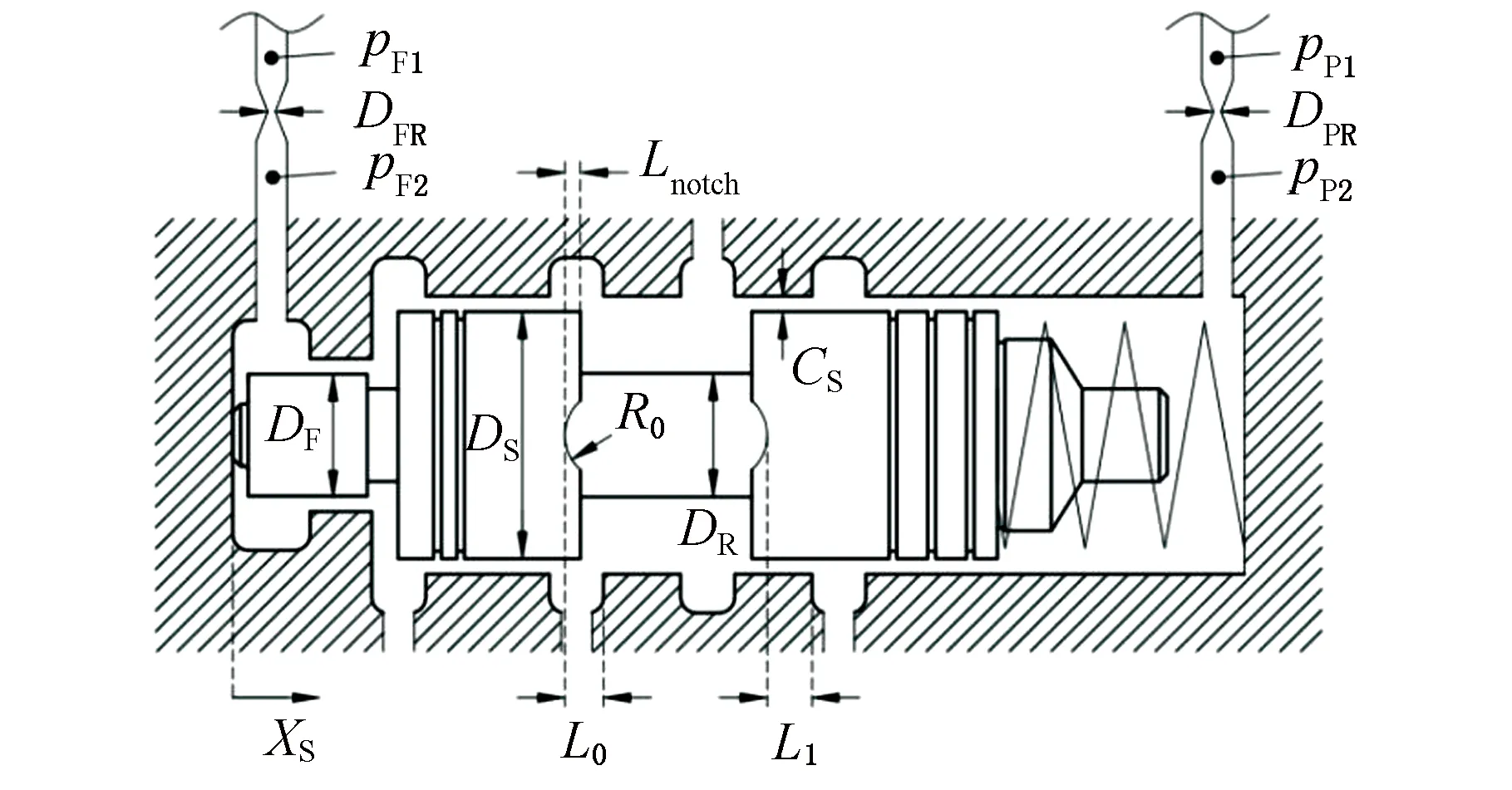
图6 滑阀参数示意图Fig.6 Schematic overview of cross-sectionof reduction spool
根据滑阀在阀孔中的行程,进油口的面积A?in可分为3种情况来计算,如图7所示。
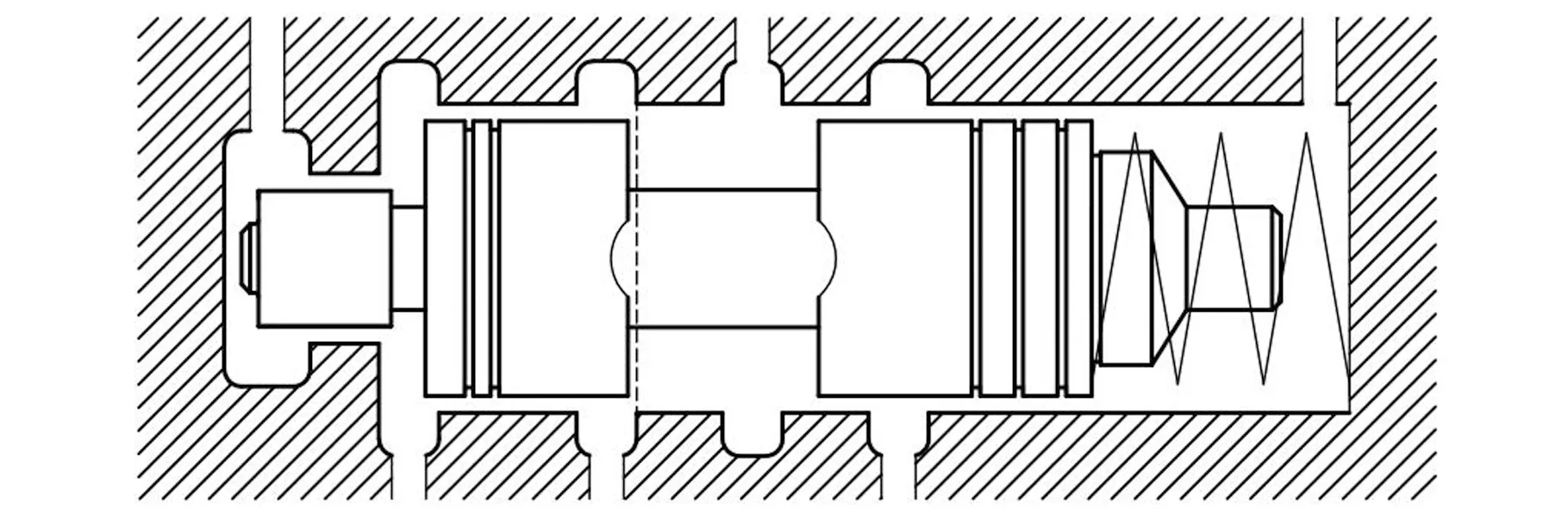
(a)进油口节流槽全开
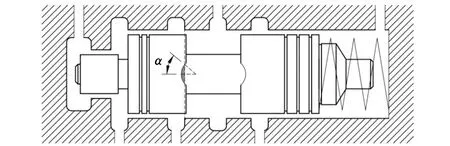
(b)进油口节流槽半开
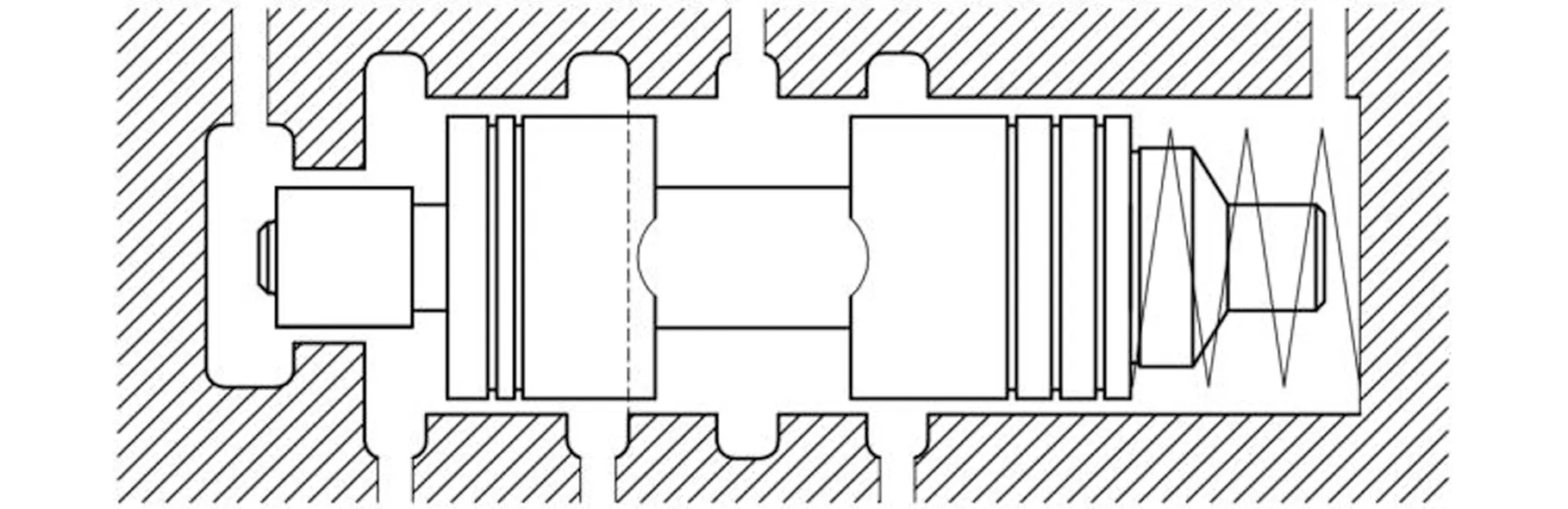
(c)进油口节流槽全关图7 滑阀节流槽位置状态示意图Fig.7 Schematic overview of situationsof spool valve notch
(1)0≤X?S≤L?0-L?notch时:
A?in=min(A?in,1,A?in,2)
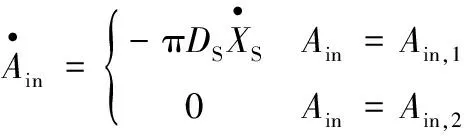
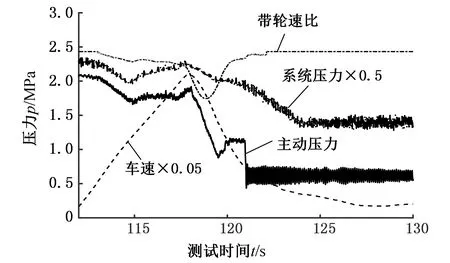
(2)L?0-L?notch A?in=2R?0[αR?0-sinα?(R?0+X?S-L?0)] (3)L?0≤X?S时: 根据上述公式可知,节流槽进口面积在滑阀全运动行程范围内为分段非线性参数。 当进油节流槽处在临界位置(进油口刚打开)时,泄油节流槽距阀口距离即为密封距离L?s: L?s=L?1-L?0 先导阻尼孔压降公式为 反馈阻尼孔压降公式为 其中,p?P1、p?P2分别为先导阻尼孔前、后压力;p?F1、p?F2分别为反馈阻尼孔前、后压力,并且p?F1为主动滑阀输出到主动油缸的控制压力。滑阀详细受力公式见文献[20]。 灵敏度分析是研究不同输入变量在各自不同定义范围内对系统输出变化影响的贡献程度,从而确定系统的关键设计变量,为设计和优化提供关键指导作用。 Sobol’基于Monte Carlo理论,将目标分析函数f?(X?)按照随机影响因素进行高维展开成单个和多个随机变量函数的和[12]: f?12…k?(x?1,x?2,…,x?k?) (3) 式中,k?为随机因素个数。 在输入变量变化范围中进行随机采样,生成随机变量矩阵,并对输出结果进行方差分析。 Sobol’全局灵敏度分析主要提出2个指标:一阶灵敏度影响因子S?i?,代表第i?个随机变量对目标函数总方差的独立影响[9];全局灵敏度因子S?Ti?,代表第i?个随机变量对目标函数总方差的独立影响及和其他随机变量交叉作用的影响[11]。为实现指标计算,最关键的是生成2个随机变量原始矩阵A、B,并参照文献[15]的方法生成衍生矩阵。文献[10,15]给出了方差的具体计算公式: 故x?i?的一阶灵敏度S?i?、一阶全局灵敏度S?Ti?、以及x?i?和x?j?2个参数的二阶灵敏度S?ij?分别为 2.2.1评价指标 在减压回路中,压力脉动与减压阀及其相关附件有关,其系统可进行如下简化:滑阀简化为质量,阀口压降损失和黏性摩擦损失及先导/反馈阻尼孔等简化为阻尼,与弹簧构成单自由度质量弹簧阻尼系统。根据前述模型,可以计算此系统在简谐压力的激励下的输出压力响应。设系统在减压阀前端供给简谐压力,压力脉动峰值为Δp?b,经过减压阀后脉动峰值为Δp?a,定义减压阀的压力脉动衰减率为 结合式(3),定义压力脉动衰减率K?at为目标分析函数f?(X?),其中X?为输入参数变量。根据减压回路的关键参数公式及泄漏量测试结果,选取12个参数(即k?=12)作为随机输入因素,如表1所示。其中,因素均为均匀分布,节流槽直径D?n=2R?0。 2.2.2仿真运算流程 在减压阀及蓄能器阀芯运动过程中会受到液动力、库仑力等非线性因素的影响,本文在AMESim中建立减压阀控制模型,如图8所示。 通过MATLAB生成各变量随机采样序列,并驱动AMESim模型进行联合仿真,最后在MATLAB中分析计算所需灵敏度参数,具体仿真流程如图9所示。其中由于A、B及衍生矩阵均为分布在[0,1]范围内的随机数,而通过表1可知随机因素最小值x?i?,min和最大值x?i?,max,但其分布并不是按[0,1]进行的,需进行矩阵转化,转化公式为 表1 影响因素统计表 图8 主动减压回路AMESim模型简图Fig.8 Simplified configuration of AMESim model ofprimary reduction circuit 图9 仿真流程简图Fig.9 The calculation process of simulation 2.2.3仿真收敛性验证 对于采样算法,分布均匀的低差异(low discrepancy)随机数意味着更优秀的样本分布,而好的样本分布直接影响计算的收敛速度。由于Sobol’灵敏度计算次数为2N?(k?+1),直接与采样样本量N?及设计输入参数k?有关,因此选择低差异随机数生成算法对计算快速收敛性及结果的准确性有重要意义。本文利用MATLAB自带随机数生成算法生成Sobolset低差异准随机数。 在零部件加工中,零件实际尺寸经常分布在名义尺寸附近,符合正态分布规律。为了探讨各输入变量在合理边界范围内的不同影响,不分析名义尺寸及公差带选用的合理性,采用[0,1]均匀随机分布原则,如表1所示。 为保证计算效率及结果的准确性,参照文献[21]方法,选取先导阻尼孔的一阶灵敏度作为观察指标,进行样本量独立性验证(收敛性验证)来选取合适的N?值。收敛性验证结果如图10所示。 图10 采样次数收敛性验证Fig.10 Convergence verification of sampling number 据图10可知,在采样次数超过210后,一阶灵敏度观察指标基本收敛,故本文N?取211次。 在CVT使用过程中,低频率的压力波动会使金属带打滑造成变速器寿命降低甚至断带失效。为验证带轮减压阀模型参数对不同频率压力脉动的衰减特性,分别给出频率为10 Hz、30 Hz、50 Hz,振幅为0.6 MPa的前端输入激励。仿真分析结果如表2所示。 Tornado图不仅能显示灵敏度大小,还可以进行随机因素的重要性排序,随机因素一阶灵敏度和一阶全局灵敏度Tornado图见图11。 通过表2及图11可知,随机因素4、9、12即先导阻尼孔直径、节流槽直径、负载阻尼孔直径对减压阀压力脉动影响较大,为进一步识别这3个参数的耦合影响强度,特进行二阶灵敏度仿真,结果如表3所示。用Tornado图进行二阶灵敏度表示,见图12。 表2 Sobol’一阶、一阶全局灵敏度结果 表3 Sobol’二阶灵敏度结果 3.2.1一阶灵敏度、一阶全局灵敏度结果分析 根据表2及图11可知,蓄能器的直径和质量及弹簧刚度、减压阀的直径和质量及弹簧刚度、配合间隙、密封距离的一阶灵敏度及全局灵敏度均较小;反馈阻尼孔的一阶灵敏度排第4,一阶全局灵敏度也排第4。而先导阻尼孔直径、节流槽直径、负载阻尼孔直径在10 Hz的前端激励下一阶灵敏度分别为0.493 4、0.128 6、0.076 6,在30 Hz时分别为0.444 8、0.112 2、0.061 8,在50 Hz时分别为0.428 0、0.109 2、0.057 3,依次排第1、第2、第3,3个参数一阶全局灵敏度排名一致,但是节流槽直径一阶全局灵敏度在10 Hz时为0.513 8、30 Hz时为0.572 3、50 Hz时为0.576 1,比其一阶灵敏度10 Hz时的0.128 6、30 Hz时的0.112 2、50 Hz时的0.109 2均增大较多;负载阻尼孔直径一阶全局灵敏度在10 Hz时为0.434 8、30 Hz时为0.483 9、50 Hz时为0.492 8,比其一阶灵敏度10 Hz时的0.076 6、30 Hz时的0.061 8、50 Hz时的0.057 3均增大较多;而先导阻尼孔直径一阶全局灵敏度在10 Hz时为0.654 1、30 Hz时为0.660 9、50 Hz时为0.654 0,相比其一阶灵敏度10 Hz时的0.493 4、30 Hz时的0.444 8、50 Hz时的0.428 0均增大较少。节流槽直径和负载阻尼孔直径的一阶全局灵敏度较一阶灵敏度增大较多,说明这2个因素对全局影响相对较大,而在其他因素变化时,二者输出影响即一阶灵敏度相对较小。反馈阻尼孔的一阶灵敏度、一阶全局灵敏度变化不大,这说明其他因素变化或反馈阻尼孔单独变化时,对输出影响较小。当减压回路前端供给压力波动频率从10 Hz到30 Hz再到50 Hz变化时,先导阻尼孔直径、滑阀节流槽直径、负载阻尼孔直径的灵敏度一直保持较高水平,由此可以证明减压回路在设计或优化时要重点考虑三者的设计参数。 一阶灵敏度S?i? 一阶灵敏度S?i? 一阶灵敏度S?i? (a)f?=10 Hz (b)f?=30 Hz (c)f?=50 Hz 一阶全局灵敏度S?Ti? 一阶全局灵敏度S?Ti?(c) 一阶全局灵敏度S?Ti? (d)f?=10 Hz (e)f?=30 Hz (f)f?=50 Hz图11 随机因素一阶灵敏度和一阶全局灵敏度Tornado图Fig.11 Tornado figures of the first order and total order effects of Sobol’ sensitivity index 二阶灵敏度S?ij? 二阶灵敏度S?ij? 二阶灵敏度S?ij? (a)f?=10 Hz (b)f?=30 Hz (c)f?=50 Hz图12 随机因素组合二阶灵敏度Tornado图Fig.12 Tornado figures of the second order effects of Sobol’ sensitivity index 3.2.2二阶灵敏度结果分析 根据表3及图12可知,随机因素4、9即先导阻尼孔直径、滑阀节流槽直径的二阶灵敏度在10 Hz时为0.049 2、30 Hz时为0.063 8、50 Hz时为0.068 9,均较小,说明二者对减压回路耦合影响较小;随机因素4、12即先导阻尼孔直径、负载阻尼孔直径的二阶灵敏度在10 Hz时为0.051 9、30 Hz时为0.047 2、50 Hz时为0.054 9,均较小,说明二者对减压回路耦合影响也较小;而随机因素9、12即滑阀节流槽、负载阻尼孔二阶灵敏度值在10 Hz下为0.416 7、30 Hz下为0.379 8、50 Hz下为0.373 7,均较大,说明二者对减压回路的耦合影响很大。因此在执行机构已经确定的情况下,减压阀的节流槽必须根据液压执行机构在不同工况下的流量需求(即负载阻尼孔流量需求)来进行设计。 根据前述灵敏度分析结论,对某型号CVT变速器样机进行实车道路测试。如图13所示,在测试过程中发现,主动压力阶跃变化时没有快速收敛,反而发生了低频压力脉动,压力脉动幅值Δp?a为0.13 MPa,频率为11 Hz,具体故障数据如图14所示。 图13 实车测试Fig.13 The picture of the car test 图14 主动压力脉动故障段数据图Fig.14 The fault data picture of the primarypressure fluctuations 根据液压系统原理图搭建仿真模型,导入实时工况数据和泄漏数据进行仿真验证。由于主被动油缸参数已定(即等效负载阻尼孔已确定),根据灵敏度分析结果选取先导阻尼孔及圆形节流槽直径作为优化变量。其中优化前,D?n=6 mm、D?PR=0.8 mm。 响应曲面法(response surface methodology,RSM)作为一种数理统计方法,被广泛应用于产品开发设计、参数和故障优化,它利用DoE方法根据输入变量及输出结果进行多项式回归分析,泛化能力强、预测精度高[22-23],并且通过3D曲面可以直观显示结果与输入变量的关系,因此本文利用RSM方法,采用中心组合的方式对压力脉动进行虚拟仿真,再进行二次回归分析,得出响应面模型,见图15。 图15 主动压力脉动幅值响应曲面Fig.15 Response surface of pressure fluctuations amplitude 响应面多项式如下: 二元函数极值求解方式如下: (1)当AC?-B?2>0时,A?>0,具有极小值;A?<0,具有极大值。 (2)当AC?-B?2<0时,无极值点。 据此对压力脉动幅值Δp?a进行优化,求得压力脉动幅值极小时,D?n=3.07 mm,D?PR=1.15 mm,圆整可得D?n=3 mm,D?PR=1.2 mm。根据优化分析结果进行样件改进加工,如图16所示;并进行试验测试,优化前后数据如图17所示。 图16 优化前后样件对比Fig.16 Sample comparison before and after optimization 图17 优化前后数据对比Fig.17 Test data comparison before and after optimization 根据图17可知,优化样件经测试,其主动压力在同等工况下快速收敛,脉动幅值大幅度降低,具体见表4。 此验证结果符合韩国现代摩比斯KIM等[24]的分析结论,因此进一步说明采用Sobol’灵敏度识别减压回路压力波动关键参数方法的有效性。 表4 优化前后数据对比结果 (1)本文引入了Sobol’灵敏度算法对减压回路在不同频率激励下压力脉动衰减特性参数进行了分析,其一阶灵敏度及一阶全局灵敏度结果显示先导阻尼孔、滑阀节流槽、负载阻尼孔直径对压力脉动的衰减有重要作用。 (2)通过对模型的进一步分析,计算Sobol’二阶灵敏度,结果表明滑阀节流槽和负载阻尼孔对压力脉动的衰减有很强的耦合作用,因此节流槽必须根据实际负载来进行设计。 (3)利用灵敏度分析结论对压力脉动故障进行优化,优化后,故障现象经试验验证得到了明显改善,证明了灵敏度分析方法的有效性。本文的研究结果对液压减压回路的设计和故障分析优化均具有指导意义和参考价值。2 Sobol’灵敏度分析及应用原理
2.1 Sobol’灵敏度分析算法

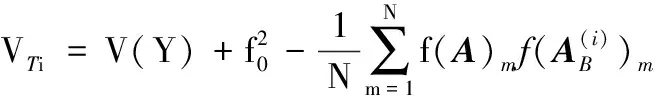

2.2 Sobol’灵敏度仿真应用方法

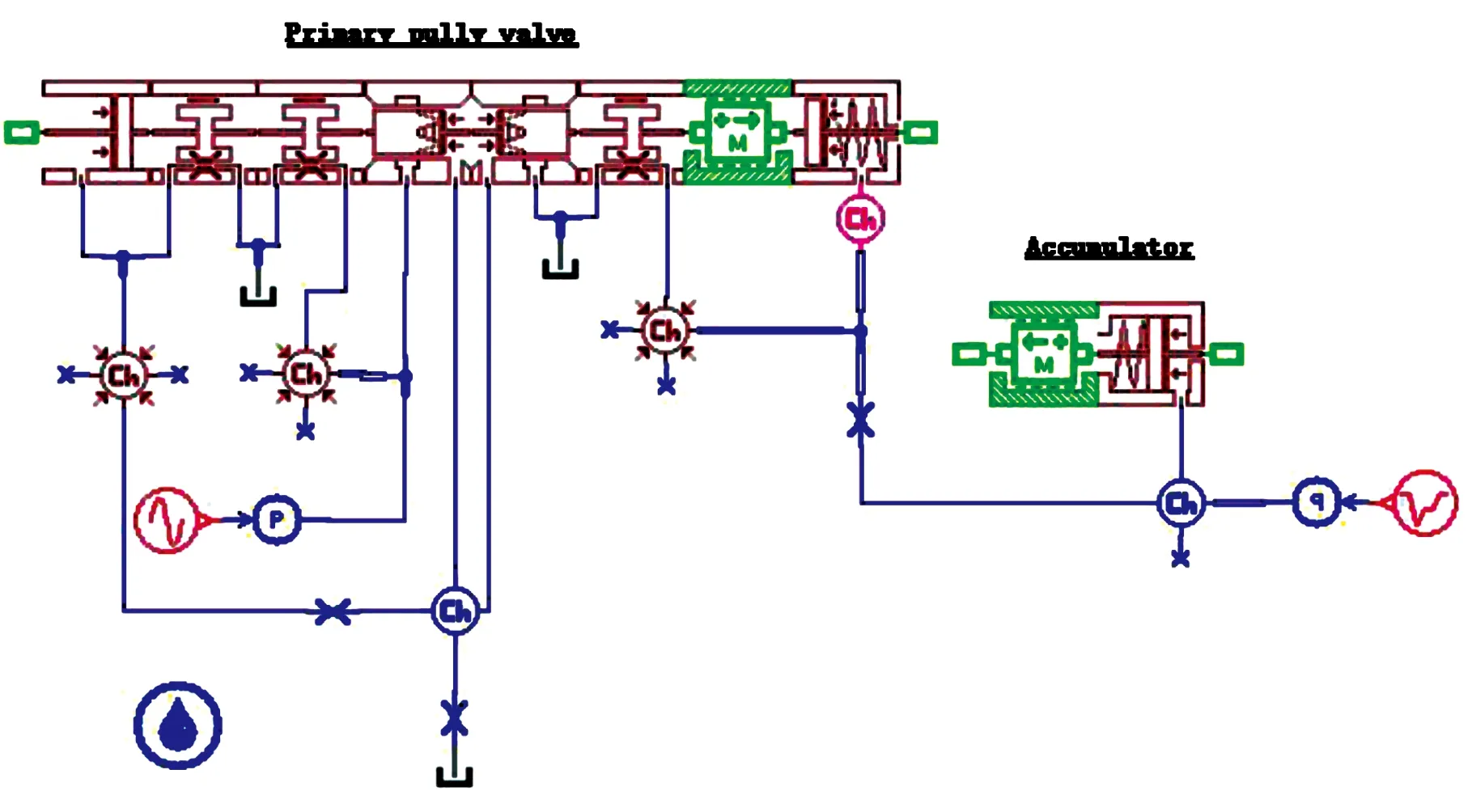

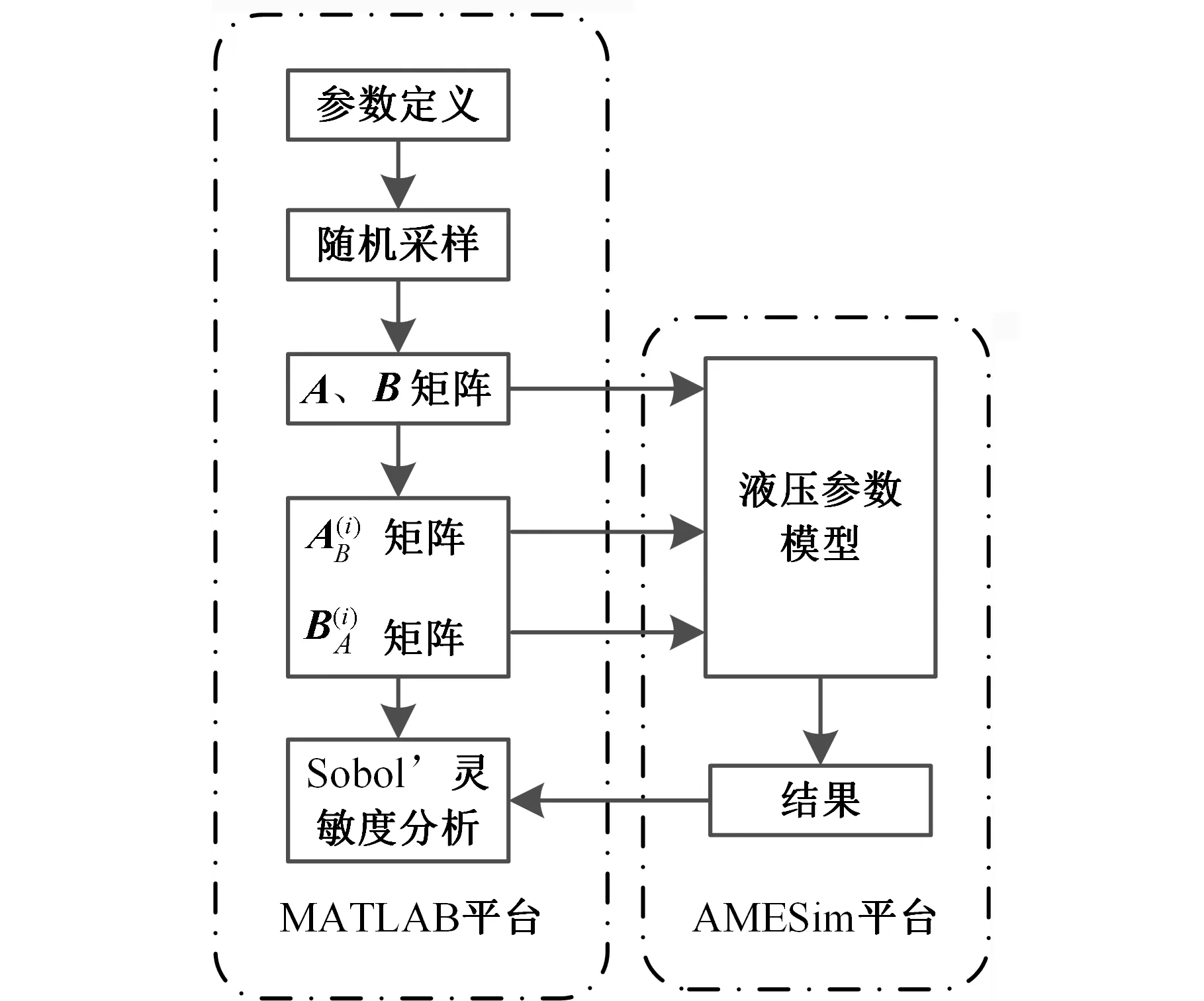
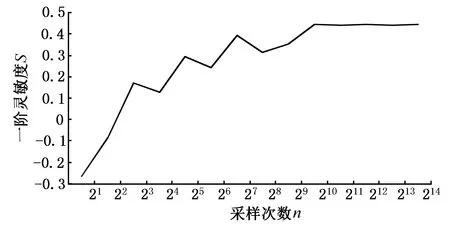
3 Sobol’灵敏度仿真及结果分析
3.1 灵敏度仿真结果
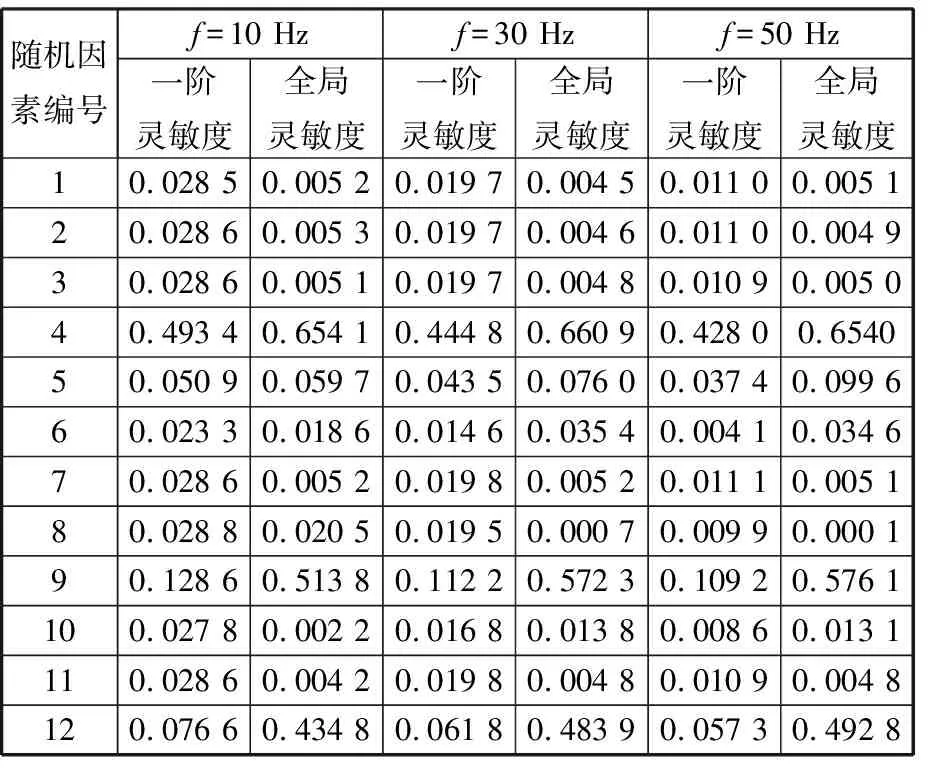

3.2 仿真结果分析



4 试验及优化验证





5 结论
