预紧载荷下螺栓结合部静特性分析
2019-05-31黄玉美李鹏阳
惠 烨 黄玉美 李鹏阳 李 艳
1.陕西科技大学机电工程学院,西安,710021 2.西安理工大学机械与精密仪器工程学院,西安,710048 3.教育部数控机床及机械制造装备集成重点试验室,西安,710048
0 引言
在机床设计阶段,预估整机的特性是当前研究的热点。对机械系统中各构件单独进行有限元分析均能得到较高的精度,也能与试验数据具有良好的一致性,但构件装配后进行分析时,构件间各种机械结合部的存在及其不相容性、非线性等特性[1-2],使分析的准确性显著降低[3-4]。机床部件和床身间存在大量的螺栓结合部,螺栓结合部是由多个平面结合面和螺纹结合面组成的复杂结合部,它在受预紧载荷的状态下承受外载荷。若能提供螺栓结合部的结合条件,在有限元中建立包含结合部特性的分析模型,就能更准确地得到机械系统真实变形情况,有助于确定机床刚度及进行机床性能预测。
结合部构件的接触表面加工方法、表面粗糙度和纹理等导致结合面在受载状态下反映出非线性性质,使结合部建模及分析难度增大,很多学者对含有螺栓结合部的建模进行了研究。文献[5-9]都是将结合部构件整体建模或将刚度定义为恒定值,忽略构件间粗糙结合面的影响,建立的分析模型较粗糙,分析结果与实际结合状态偏差较大。考虑螺栓结合部的非线性特性的影响,文献[10]在对螺栓结合部分析中用4个弹簧的刚度值等效每个螺栓建立螺栓结合部模型;文献[11]利用具有不同刚度的两个非线性弹簧分别表示,对螺栓承受拉伸和压缩时的结合部特性建立分析模型;文献[12]利用弹簧-阻尼动力学单元建立结合面刚度-阻尼模型并进行了动力学分析。这些方法理论上比较完善,但其弹簧刚度计算方法复杂,尤其是多螺栓作用时弹簧参数难以准确测定,使得在建模中难以实现。
本文基于结合面基础特性参数等效出相应的虚拟材料来描述螺栓结合部的不同结合表面的特性,将等效材料的弹性常数解析解嵌入有限元解析过程,获得含有结合部的解析模型,得到比较准确的构件变形。结合试验结果将构件变形从测量值中分离出来,获得结合部变形,并与理论计算进行对比验证。
1 单螺栓结合部解析模型
为解析方便,假设螺栓结合部的结合状态是简单结合状态,即各构件在结合部处受力发生变形后,结合面仍保持原有的平面或曲面形状。
如图1所示,螺栓结合部的结合面包括两构件之间的平面结合面B,螺栓头与构件1之间的较小的平面结合面C,还包括构件2与螺栓的螺纹之间的螺纹结合面A。螺栓结合部单元的坐标系∑O?原点在平面结合面B上,X?2方向为结合面B的法向,X?1、X?3分别为结合面B的切向,X?1、X?2、X?3表示结合部的线位移方向,X?4、X?5、X?6表示结合部的角位移方向。

图1 螺栓结合部坐标系Fig.1 Coordinate system of bolt joint
螺栓结合部受载后,外载荷力和力矩列阵
F=[F?1F?2F?3F?4F?5F?6]T
式中,F?1、F?2、F?3为沿坐标系的X?1、X?2、X?3方向承受的力;F?4、F?5、F?6为沿坐标系的X?1、X?2、X?3方向承受的力矩。
结合部反力和反力矩列阵
FJ=[F?J1F?J2F?J3F?J4F?J5F?J6]T
设p?1、p?2、p?3为沿坐标系X?1、X?2、X?3方向结合部单位面积上的反力,则有
(1)
(2)
式中,α?n、β?n为结合面法向基础特性参数;α?τ、β?τ为结合面切向基础特性参数;λ?2为结合面法向变形;λ?1、λ?3为结合面切向变形;φ?λ?2为方向判别函数。
螺栓结合部力平衡方程为
F+FJ=0
(3)
那么:
(4)
式中,ΔP?i?为外载荷引起的螺栓连接力的变化量;P?i?为第i?个螺栓所受的预紧力;A?i?为第i?个螺栓的截面积;l?为螺栓的连接长度;E?为材料的弹性模量;a?为考虑螺纹接触面变形影响系数;X?1i?、X?3i?为第i?个螺栓在结合面中的坐标值。
设螺栓结合部承受外载荷后产生的相对位移
U=[U?1U?2U?3U?4U?5U?6]T
在螺栓承受外载荷后将外载荷向坐标原点O?等效。根据螺栓结合部受力后是简单结合状态的假设,在结合面中任意接触点(X?1,X?2,X?3)处,结合部单元的接触变形为
λ=[λ?1λ?2λ?3]T
(5)
λ?1=-U?1-X?3U?5
λ?2=λ?p2-U?2-X?1U?6+X?3U?4
λ?3=-U?3+X?1U?5
式中,λ?p2为沿X?2的法向预变形。
结合部在受到各向载荷同时作用时,不仅某一单向载荷与变形之间成非线性关系,各载荷之间也成非线性耦合关系,由式(1)~式(5)知F是U的函数,但数学模型中含有6个未知量,且为非线性隐含积分方程组,无法直接求导。采用弦截法求解可以避免求高阶导数,减少计算量,收敛速度也较快,但弦截法判断曲线的凹向条件要计算二阶导数。为了对螺栓结合面位移进行精确计算,采用改进变量轮换弦截法编程求解,将所求的多个变量赋予初值后,采用不断替换区间端点的方法来改进求取变量值,对求解模型中每个方程轮换进行验算,直至每个方程都满足给定精度才输出所求变量值,迭代求解位移流程见图2。

图2 迭代求解位移流程图Fig.2 The flowchart for solving the displacement
2 螺栓结合部单元有限元分析
建立分析模型,用有限元分析软件分析结合部变形,需设定构件材料的弹性模量、泊松比等参数,这些材料常数能够反映构件的力学性质,但不能直接反映构件在结合部处的力学性质,很难在构件中直接表示螺栓结合部的非线性性质,使得螺栓结合面的有限元建模精度较低、误差较大,影响分析结果的准确性。螺栓结合部由多个结合面组成,文献[6]的研究结果表明,在有限元建模中不需要某些细节特征(如螺纹)相互作用进行建模来保证结果的有用性,因此在以下的建模中只考虑平面结合面,暂不考虑螺纹结合面的影响。
如图3所示,建模时将含有结合部的模型在平面结合面B处通过增加一个等效虚拟材料层构件表示结合部特性,通过设置虚拟材料层构件的弹性模量、泊松比和密度来模拟结合部力学特征,并进行迭代计算获得预紧状态下构件的变形。
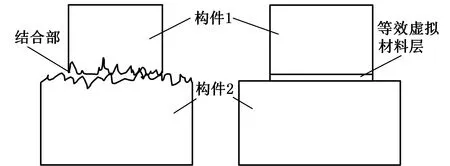
(a)结合部结构 (b)含有等效虚拟材料层模型图3 模型的建立Fig.3 Model establishment
2.1 等效虚拟材料层参数的获取
2.1.1等效虚拟材料层的材料参数
结合部的特性影响因素多、且为非线性,与构件结构无关的结合面固有特性因素包括结合面的材质、加工方法、表面粗糙度、纹理、结合面间的介质等[13]。结合面基础特性参数是针对结合面固有特性各因素基于实际结合状态获取的数据,能够反映结合面实际条件的影响,本文根据结合面基础特性,给出等效虚拟材料层的材料参数来描述螺栓结合部结合表面的特性。
对于小面积接触单元,假定法向面压p?n均布且与法向刚度k?n成线性关系,当法向载荷P?n=p?nA?(A?为接触面积),结合面上由法向刚度k?n产生的法向虚功
(6)
式中,Δh?为变形量。
由材料应变能相等的原则,把离散的单元折合为连续的等效虚拟材料弹性体后,得出折算单元内的总的法向应变能
(7)
式中,σ?z为作用在单元面内的平均横向应力;h?为接触面厚度。
由W?1=W?2得
E?=k?nh?
(8)
同理,可得到在切向剪切载荷P?τ作用下,折合后材料的切变模量
G?=k?τh?
(9)

(10)
对于螺栓结合部,单位面积上的刚度
(11)
k?τ=α?τλ?nβ?τ
(12)
式中,λ?n为结合面法向变形。
根据螺栓结合部所受的法向面压p?n,由式(3)、式(11)、式(12) 可得首次求解时面单元的基础特性刚度法向刚度k?n和切向刚度k?τ,代入式(8)、式(10)得到虚拟材料的法向弹性模量E?和泊松比ν?。
设ρ?1、ρ?2为两零件材料的密度,h?1、h?2为两零件微观不平的表面层厚度,参考文献[14]等的研究结果,等效虚拟材料的平均密度可为
(13)
2.1.2虚拟材料层的厚度
建立等效虚拟材料层构件模型需设置与结合表面层结构相近的厚度,经过不同的机械加工方式,结合面表面组织结构和几何形貌凹凸不平,典型的金属表面层结构如图4[15]所示。在金属基体之上的轻、重变形层是材料加工强化层,变形层的厚度与金属加工工艺过程有关,不同的金属加工工艺和表面粗糙度会导致表面变形层的厚度不同。

图4 金属表层结构Fig.4 The structure of metal surface layer
为获得材料表面变形层厚度,文献[16]对材料表面进行了不同加工速度的磨削试验,获得表面变形层的厚度值。但机械结合面的加工方式多样,本文对试件材料在车削、铣削、磨削3种不同加工方法下达到表面粗糙度Ra?=0.8 μm 的加工表面硬化层组织形貌做了对应的材料学试验。对不同加工方法的加工试样显微形貌分别进行显微组织分析和硬度检测,检测分析结果如图5所示,试验结果表明,在距材料表面深度约为30~130 μm附近截面的硬度接近材料心部硬度,分析可得到材料表面变形层的厚度约为30~130 μm。
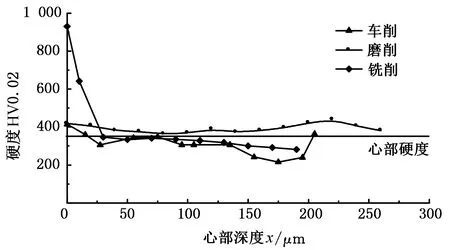
图5 试件显微硬度沿截面分布曲线Fig.5 The micro hardness distribution curve along the section
由图4可知,结合表面层总厚度h?i?近似为
h?i?=0.000 3~0.003+0.01+0.02+1+
30~130=31.010 3~131.023 (μm)
(14)
等效虚拟材料层的厚度h?是结合部两个接触表面层厚度之和,当两结合面材料相同且表面粗糙度均为Ra?=0.8 μm时,取分析模型厚度为结合表面层较厚值h?=2h?i?≈260 μm。
2.2 有限元模型的建立及迭代分析
以灰铸铁构件试验为基础,建立了与预紧试验装置中相同尺寸条件的三维模型,模型中上下构件间加入等效虚拟材料层构件以表征结合部特性。将模型导入ANSYS进行分析,构件材料参数按照与试验条件相同设置,虚拟材料层的材料参数按2.1节计算结果设置,等效材料层与上下构件间设置为绑定连接,划分网格后施加与试验情况相同的螺栓预紧载荷进行分析。
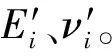
3 螺栓预紧载荷试验与算例对比验证
为验证螺栓结合部数学模型的正确性,本文在对预紧状态下的螺栓结合部进行解析计算获取载荷位移曲线的同时,设计了试验装置进行试验验证。

图6 迭代分析过程中的虚拟材料层模型Fig.6 Virtual material layer model in iterative analysis
螺栓结合部构件间的连接包括用螺钉连接和螺栓螺母连接两种方式,可统称为螺栓连接。已有的螺栓结合部的试验研究大多采用螺栓螺母的连接方式,且试验中采用的上下构件厚度相当,上下构件为通孔,下构件受力后的变形较大。在实际机床螺钉连接中,有通孔的被连接件厚度较小,带有螺纹孔的被连接件一般厚度较大,工程实际中更多采用螺钉连接。例如:内燃机缸盖和机体之间及主轴承盖和机体之间的高强度螺钉连接等。因此,本试验采用工程常用的螺钉连接方式,螺钉与下构件螺纹连接,下构件厚度较大,其变形可以忽略不计。
试验装置如图7所示,上下构件结合表面经磨削加工粗糙度均为0.8 μm,上构件厚度H?1分别为18 mm,20 mm,22 mm,下构件厚度H?2为40 mm,使用专门加工用于施载的M12的粗牙螺纹螺钉将两个构件连接起来。在施载元件、力传感器、结合面试件之间加载力传递的路线上,通过结构设计以保证加载力的对中性,不产生附加力矩;试验装置的结构中设计了轴承以避免加载时螺钉转动对力传感器的影响;力传感器直接测得螺栓的预紧力,定位环及各零件之间的尺寸配合保证了加载过程中加载力的对中性;为了使上构件受力面积与螺栓实际作用时表面的面积一致,在上构件上方设计了模拟螺栓头,使上构件承载面尺寸与螺钉实际作用时的尺寸一致,相当于螺钉头直接作用于上构件。

(a)试验装置结构

(b)试验装置实物图7 预紧试验装置Fig.7 Pre-load test device
试验过程中旋紧螺钉通过FUTEK单向力传感器监测控制预紧力的大小,分别施加预紧力0~12 kN,逐渐加载后逐渐卸载,位移传感器检测上下构件间的相对位移值(包括上构件变形和结合部变形)。由于测量结果的位移值很小,为保证测量精度,选用了6个米铱u05电涡流位移传感器在φ65的直径上均匀分布,试验中通过各种措施尽可能减小传感器信号波动,避免测量设备的读数漂移;并且进行多次测量,将6个传感器测得的结果中误差较大的值去除,以保证测量值的准确性。
3.1 试验结果比较分析
选取构件材料为HT250的试验结果进行分析,如图8所示。对于不同厚度的上构件,随着预紧力的增大,测点的相对位移均逐渐增大,呈非线性变化;在施加载荷为0~5 kN时,结合面面压小于2.5 MPa,属低面压区,上下构件相对位移变化值明显呈快速非线性变化;当预紧载荷在5~12 kN时,结合面面压在2.5~6 MPa的中高面压区,随着载荷的增大,相对位移非线性变化减缓明显;试验值与计算值接近,但存在一定误差。
试验结果表明,预紧载荷-位移曲线呈非线性,这是因为结合部的接触表面在机械加工过程中不可避免地产生形状误差、波纹度及粗糙度等,使得在受压过程中实际接触面积小于名义接触面积,表面微观凸起在接触过程中的弹性、弹塑性变形等,均会导致接触面压力和接触变形之间的非线性关系。由试验结果结合材料学原理分析,在仅受法向预紧载荷情况下,面压p?n在0~2.5 MPa时,接触表面微小突起引起的变形占接触表面层变形的比例最大,变形的非线性最强,构件自身变形影响较小;当面压p?n在2.5~6 MPa时,接触面微小突起引起的变形比例下降,构件的弹性变形影响比例增大,结合部变形的非线性减弱。
试验结果还表明,试验测得位移值与理论计算值之间存在偏差,上构件越薄、载荷越大,上构件受力后自身变形越大,引起位移值与计算值间的偏差越大。随着上构件厚度的增大,测得的上下构件之间的位移值与理论计算得到的计算值更加接近。试验构件厚度不同引起的构件本身的变形对试验结果有较大的影响。这说明螺栓结合面的接触变形与构件变形存在耦合关系,测得的位移值是整体变形,包含了结合部变形与上构件自身的变形,为获得准确的结合面变形,需要将结合面变形从所测的整体变形中分离出来。
3.2 不同建模分析及结果比较
利用有限元软件对预紧试验进行模拟分析,对试件不考虑结合部影响和考虑结合部影响(包含虚拟材料层)分别建立分析模型,迭代计算结束后读出上构件在试验测点处的变形值;从测量的整体变形量中减去有限元解析得到的试件变形量,获得不同预紧载荷下的螺栓结合部变形。
以上试件材料为灰铸铁,厚度H?1=18 mm,预紧载荷从1 kN增加到12 kN的过程为例,表1所示为将试验测得的整体变形量减去直接建模分析得到的上构件变形量,所得的结合部变形量和计算量结果的比较;表2所示为将试验测得整体变形减去考虑结合部影响含有虚拟材料层建模分析得到的上构件变形量,所得的结合部变形和计算量结果比较。由表1、表2可知,整体变形量减去含有虚拟材料层的分析模型的上构件变形量得到的结合部变形值更加接近理论计算值,误差比直接建模明显减小。
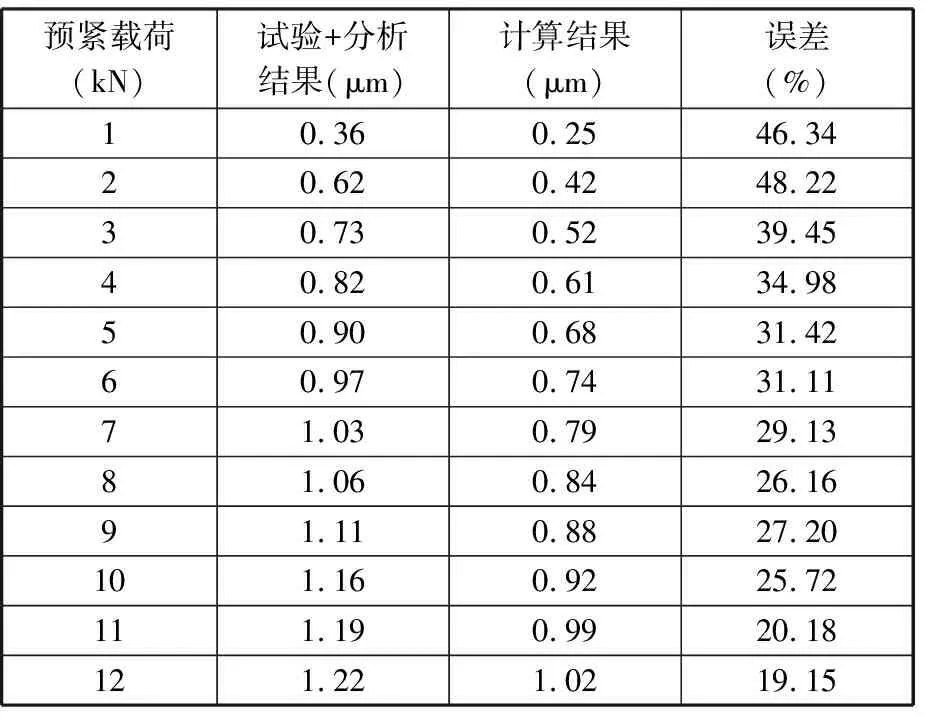
表1 直接建模分析

表2 考虑结合部建模分析
在对包含螺栓结合部的结构进行分析的过程中,将上述试验分析结果和计算结果对比,建模时基于基础试验获取结合面基础特性参数的虚拟材料层来考虑结合部的影响,获取的结果更接近螺栓结合部在受载情况下实际产生的弹塑性变形和塑性变形的非线性特性,证明了加入虚拟材料建模分析的方法可用于螺栓结合面特性分析。
4 结论
(1)本文以获取的单位面积结合面基础特性参数为基础,建立了螺栓结合部数学模型,并采用变量轮换弦截法求解得到预紧载荷作用下的结合部位移。
(2)给出了一种基于结合部基础特性参数获取结合部等效虚拟材料层材料参数的方法,建立了包含结合部特性的有限元分析模型,对承受预紧力状态下的螺栓结合部进行了精确的分析,应用分析结果将结合部变形从试验结果的整体变形中分离出来,获得了更精确的结合部变形。
(3)开发了一种获取螺栓结合面单元在预紧载荷下结合面静态特性的试验装置及试验方法,并进行了不同厚度的构件在预紧载荷下的试验。试验分析结果与计算一致,验证了本文所建立的模型的正确性。
