金沙江“10·10”白格堰塞湖溃坝洪水反演分析

陈 祖 煜，张 强，侯 精 明，王 琳，马 利 平

(1.西安理工大学 省部共建西北旱区生态水利国家重点实验室, 陕西 西安 710048; 2.中国水利水电科学研究院 岩土工程研究所, 北京 100048)

2018年10月10日22：06，西藏自治区昌都市江达县波罗乡白格村和四川省甘孜藏族自治州白玉县交界处金沙江河道右岸发生大规模山体滑坡，堵塞金沙江干流河道，形成白格堰塞湖。12日17：15堰塞湖开始漫溢自然过流，13日14：30基本退至基流，22：00险情解除。此次泄流，西藏共转移安置群众13 637人，云南共转移群众11 550人，无人员伤亡，下游在建的叶巴滩、苏洼龙水电站导流洞过流，造成一定损失，但影响可控。

堰塞湖溃决洪水过程线通常是通过量测水位降落的过程获得。但是，由于“10·10”堰塞湖在两天后即发生了漫顶溃决，相应的水位量测设备未能准确捕捉到本次堰塞湖溃决的水位下降过程线，因而无法通过库容水位关系曲线计算“10·10”白格堰塞湖溃决洪水过程线。幸运的是，在堰塞湖下游54 km叶巴滩水文站和137 km的拉哇水文站均获得了实测洪水过程线。因此，应用洪水波演进的原理和相关的程序可以对坝址(0 km)处的溃坝洪水过程线进行反演。本文应用中国水利水电科学研究院溃坝洪水分析软件DB-IWHR和西安理工大学侯精明研发的GST洪水演进模型，通过参数敏感性分析反演获得堰塞湖的溃决洪水。

1 基础资料

“10·10”白格滑坡体积约3 500万m3，滑入河道体积约2 500万m3，堰塞体顺河长约2 km，宽约450～700 m，堰塞体整体呈左岸高右岸低之势，左岸最高点高程为3 005.0 m，右岸垭口高程2 931.4 m，堰塞体高度约61～100 m。堰塞湖从12日17：15开始漫溢自然过流，13日00:45堰塞湖坝上水位达到最高值2 932.69 m，对应蓄水量2.9亿m3。13日01:00过流明显增加，06：00过流流量达到最大值约10 000 m3/s，此后开始消退，13日14：30基本退至基流[1-2]。

在堰塞湖发生后第一时间进行了无人机拍摄，三维点云图如图1所示。主堰塞体长度为961.89 m，在溃坝发生后经过水流冲刷，形成长1 622 m、底宽80～120 m的泄流槽，泄流槽口高程约2 888 m、出口底板高程2 872 m，对应堰塞湖蓄水量约0.5亿m3。堰塞湖库容水位关系曲线如图2所示。

图1 “10·10”白格堰塞体Fig.1 “10·10” Baige Landslide Dam

图4 溃口的侧向崩塌过程等效简化Fig.4 Equivalent simplifcation of lateral enlargement process

图2 白格堰塞湖库容-水位关系曲线Fig.2 Relation of reservoir storage capacity and water level of Baige barrier lake

2 溃坝洪水水力学基础

2.1 溃口洪水分析

DB-IWHR溃坝洪水分析模型主要包括以下3个部分[3]。

2.1.1 溃口水力学条件

溃口断面处的流量计算采用宽顶堰公式，如式(1)～(2)所示。

(1)

(2)

式中，C为综合流量系数，理论值为1.7 m1/2/s[4]，建议取值1.3～1.7[5]；mb,mq分别为宽顶堰的流量系数和侧收缩系数；H为库水位；z为渠底高程。

水流经过堰口跌落后水深为h，如图3所示。流量系数m计算方法如式(3)所示，建议取值为0.8～0.6之间。

(3)

式中，h为溃口水深。

图3 宽顶堰泄流示意Fig.3 Discharge of broad crest weir

2.1.2 冲刷模型

DB-IWHR采用双曲线模型，其形式如式(4)。

(4)

式中，γ为扣除临界剪应力后的剪应力。

γ=k(τ-τc)

(5)

2.1.3 溃口侧向扩展模型

溃口横向扩展采用了岩土工程中的圆弧滑动面分析方法，并且比较合理地模拟了岩坡崩塌过程。岩坡崩塌过程如图4(a)所示。但是在实际操作时，需输入每一步的圆心坐标、半径和渠底坐标，寻找临界滑裂面，过程太过繁琐。在实际应用时，简化为一系列梯形[3]，如图4(b)所示。

根据近期研究分析，我们提出了用双曲线模型来计算梯形侧面倾角增量Δβ。

(6)

(7)

式中，1/m1和1/m2分别表示双曲线的初始切线和渐近线。文献[6]详细介绍了此双曲线模型。

2.2 洪水波演进模型

2.2.1 控制方程

洪水演进采用GAST模型，它运用平面二维浅水方程(SWES)模拟洪水演进过程，控制方程如下[7]：

(9)

式中，q为变量矢量，包括水深h，x、y方向的单宽流量qx、qy；g为重力加速度，u和v分别为x、y方向的流速；F、G为x、y方向的通量矢量；S为源项矢量；zb为河床底面高程，Cf=gn2/h1/3为谢才系数，n为曼宁系数。

2.2.2 数值方法

GAST模型相较于经典的水动力学数值模型，其数值求解格式为Godunov类型的有限体积法，它可以很稳健地解决不连续问题，并严格保持物质守恒[7]。网格中的水、泥沙和动量的数值通量应用HLLC近似黎曼求解器计算[8]。干湿边界处负水深问题通过静水重构法解决。底坡源项和摩阻源项分别使用底坡通量法和半隐式法处理[9]。时间积分采用二阶显示Runge Kutta方法进行，构造具有二阶时空精度的MUSCL型格式，能有效解决复杂地形引起的计算发散和物质动量的不守恒问题，提高了计算的稳定性[10]。并且，GST模型采用了GPU加速计算技术，大大提高了计算效率[11]。

3 溃坝洪水反演分析

金沙江电站分布如图5所示。根据实测和团队前期研究相关数据，“10·10”白格堰塞体溃坝计算参数如表1所示。以往对唐家山、易贡、小岗剑等堰塞湖反演工作表明[12-14]，冲刷侵蚀系数b是其中敏感性较高的参数。其它参数对洪峰计算影响仅在5%左右。因此，我们取b为0.000 4,0.000 5和0.000 6进行溃坝洪水计算，结果获得的溃口处的流量过程线如图6所示。

图5 金沙江部分电站分布Fig.5 Distribution of some power stations on Jinsha river

名称符号数值地理学参数库容系数p1,p2,p3,Hr0.11, 4.77, 90.20, 2910m初始库水位H02932.50m初始底高程z02929m入流流量q800m3/s库容水位关系h2910.00,2915.00,2935.00 mW90.20,116.80,278.40亿m3水力学参数宽顶堰系数C1.43跌落系数m0.8启动流速Vc4.0侵蚀参数a, b1.1000,0.0006岩土力学参数坝体材料参数c,φ,γ50kPa, 45°,18.5kN/m3溃口双曲线模型参数m1, m20.95,0.04初始溃口侧向倾角 β0129°

注：其中库容与水位关系用公式表示W=p1(H-Hr)2+p2(H-Hr)+p3

由图6可以看出，当b为0.000 6时，溃口发展到6.2 h达到洪峰流量10 882.78 m3/s，最终溃口水面宽度为99.6 m；b为0.000 5时，5.65 h达到洪峰12 261.51 m3/s；b为0.000 4时，洪峰流量最大，5.16 h即达到洪峰流量14 219.86 m3/s。不同冲刷侵蚀参数b对溃口洪峰流量计算值的影响敏感度约为30%。

GST模型主要输入参数资料为地形资料、入流资料、模拟参数，地形资料采用白格至拉哇下游处的数字地形高程数据(DEM)，全长约137 km，共计187万网格。上游边界为入流边界，采用DB-IWHR模型计算结果，下游边界为开边界的自然出流，其余边界为封闭边界。曼宁系数选用0.02，库郎数为0.5[15]，模拟时间为27 h，计算步长0.01 s。

下游模拟流量与实测结果如图7所示。

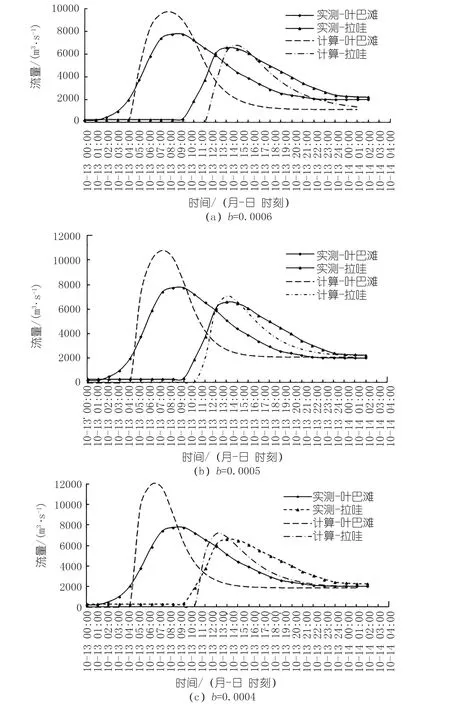
图7 模拟流量与实测过程对比Fig.7 Simulation and measured discharges of the dam break flood propagation

可以发现，图7(a)的计算成果与下游叶巴滩、拉哇的实测值最为接近。相应此工况，b为0.000 6。13日14:00洪水演进至拉哇，洪峰流量为6 786.24 m3/s，比实测推迟1 h左右，洪峰流量误差约为8 %。为此，我们将该工况相应溃口洪峰流量10 882.78 m3/s以及图6中b=0.000 6的过程线作为“10·10”白格堰塞湖溃决的反演成果。

4 结 论

本文以下游在建水电站处实测的洪水过程为依据，分别采用冲刷侵蚀参数b为0.000 6,0.000 5和0.000 4，通过DB-IWHR溃坝洪水分析程序和GST洪水演进模型，对“10·10”白格堰塞湖漫顶自然泄流过程进行了反演分析。

(1) 当冲刷侵蚀参数为a=1.100 0、b=0.000 6时，溃决洪水模拟至叶巴滩和拉哇的模拟结果和实测洪水流量过程最为接近。据此判断“10·10”白格堰塞湖历时6.2 h溃决到达洪峰流量10 882.78 m3/s，最终溃口水面宽度为99.66 m。

(2) 从不同冲刷侵蚀参数的溃坝洪水演进模拟结果可以发现：在溃决洪峰流量相差较大的情况下，洪水演进至拉哇处的洪峰流量相差较小。由此说明，洪峰流量越大，洪水演进过程中坦化作用越明显，洪峰流量到达时间提前。

(3) DB-IWHR是基于EXCEL程序VBA开发的溃坝洪水分析软件，在输入合适的参数后，即可完成计算，得到溃口流量过程。GST模型采用了GPU加速技术，在白格至拉哇137 km的大尺度空间，共计187万网格，计算时间仅半小时，计算效率大大提高。DB-IWHR溃坝程序结合GST模型在堰塞湖应急抢险的过程中，可以实现快速、精准的预测。