基于遗传算法的灰色非线性水环境管理模型及应用

周 科

(华北水利水电大学 艺术设计学院，河南 郑州 450011)

1 研究背景

在水环境规划与管理领域内，大量参数往往存在着观测主观性和不可靠性问题[1]。另外，对于一个灰色系统，对参数的不确定性问题往往是以模糊的方式描述，为了保证规划问题优化解的存在，对于代表性参数，往往会给出一个存在区间，并且会给出该区间的上下边界[2]。在实际问题中，由于水生态环境涉及的参数众多且具有不确定性，通常会选用灰色系统理论来构建水环境管理模型，以解决非确定性规划问题[3-4]。然而，灰色模型的求解势必要牵涉到非线性问题，而高度非线性问题又势必会增加优化过程的计算困难。求解灰色非线性模型的方法有多种途径，包括大规模分解协调法、动态混合整数规划法以及混沌优化法等[5-7]。前两个方法的计算结果误差很大，而混沌优化算法虽然可以获得满意的解，但是计算耗时太长。因此，为了处理非线性问题，可以应用遗传算法(GA)来搜索灰色系统内的全区域优化解[8]。除此之外，也可以将遗传算法应用于求解灰色非线性规划的环境管理问题[9]。上述研究成果大多与河流水资源开发利用规划或污水处理厂的规划运行管理有关，但是很少将河流治理工程建设、水资源开发利用、污水处理厂运行管理以及周围水生态环境改善联合协调应用。

因此，本文基于郑州市贾鲁河的治理规划，构建了灰色非线性模型。同时，选择遗传算法作为计算手段，对所构建的模型进行了求解。该模型在构建过程中也考虑到了治理区域内的污水处理厂优化运行、南水北调补水、区域内3个生态湖泊与治理河段的净化能力等。研究成果表明，基于遗传算法的灰色非线性规划在区域水环境治理中的应用潜力非常显著。

2 遗传算法(GA)分析

遗传算法(GA)是基于适者生存并遗传的一种强收敛和启发式搜索技术[10]，通过产生一组个体，初步构造由用户定义的群体，群体中的每一个个体都代表着特殊问题的潜在解。对每个个体进行编码(从0s到1s)，用目标函数对每一代群体中的个体表现进行评价，从中得到个体优化配型值[11]；然后利用个体优选配型值并基于其出现的概率，通过优选配型、交叉和突变运算，构建第二代和后续各代群体。在优化配型选择过程中，可以选择一连串的个体体系复制下一代。根据个体优化配型值，用概率法确定个体体系。计算流程如图1所示。

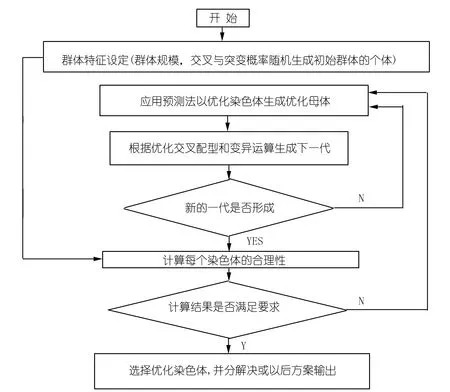
图1 水环境管理模型GA计算流程Fig.1 The procedure of GA for water environment management models

预测选择优化染色异每个求一个具有理想优化配型值的个体体系具有较大的概率参与再生，而具有不理想优化配型值的个体体系在演变过程中就有可能被淘汰。可以对优化染色体的保留策略进行集成组合以便加速收敛时间，对于两个优化配型值都很大的染色体，可以从第一代直接到第二代[12]。交叉算子可以交换模型参数，将随机选取的母体参数集生成下一代群体的新的参数集；采用两点交叉法可以生成新的个体，保留表现好的染色体[13]。突变过程是指一串个体的位置偶然或随机变化以维持一个群体的多样性的过程。因此，可以采用优化选配交叉和突变算子来维持群体的多样性[14]；也可以将若干代视为一轮GA进行运算, 直到连续几代在目标函数中都没有得到新的改善。一般来说，GA算法的效率取决于计算过程中GA算子的合理选择。

3 郑州市贾鲁河水环境管理模型构建

3.1 概 况

3.1.1 工程概况与可利用水量

贾鲁河是淮河支流沙颖河的主要支流，也是郑州市的主要排水河道。该河发源于新密与荥阳两市交界处，流经荥阳、郑州、中牟、开封、尉氏、鄢陵、扶沟、西华、周口，在周口市汇入沙颖河。河流全长256 km，流域面积为5 896 km2,其中，郑州市境内长为137 km。流域面积为2 750 km2。贾鲁河是郑州市的骨干排水河道，承担着城市防洪除涝与工业、生活污水排放及部分区域农业排水的任务。

根据2017年完成的《郑州市贾鲁河综合治理工程绿线规划》[15]，此次综合治理长度为62.77 km，从贾鲁河上游尖岗水库至中牟县大王庄弯道(开封界)。工程分3部分建设：河道绿线内治理+贾鲁湖湿地、祥云湖湿地、圃田泽湿地等3处湿地湖泊开挖+河道蓝线范围外两岸生态景观建设和河道沿线的截污治污工程。根据时间安排，工程于2017年9月底进入全面施工阶段，计划于2018年年底完成。经过治理后，实现水质还清、美化贾鲁河河道水景之目的。

郑州市贾鲁河综合治理工程规划总用水量为6 124.26万m3。其中，贾鲁河河道每年汛后的首次充水量为1 557.30万m3,贾鲁河河道蒸发损失量为317.01万m3,河道渗漏损失量为321.47万m3,河道外绿化用水量为76.28万m3,贾鲁河更新置换水量为3 852.20万m3。

规划总供水量为6 124.26万m3,水源为双桥污水处理厂再生水972.00万m3,马头岗污水处理厂再生水3 804.37万m3,贾鲁河流域尖岗水库至圃田泽之间非汛期地表径流量为1 215.00万m3,邙山泵站引黄水132.89万m3。贾鲁河综合治理水体特征现状如表1所示。

表1 贾鲁河综合治理水体特征现状统计

Tab.1 Flow capacity and water quality at Jialuhe River basin

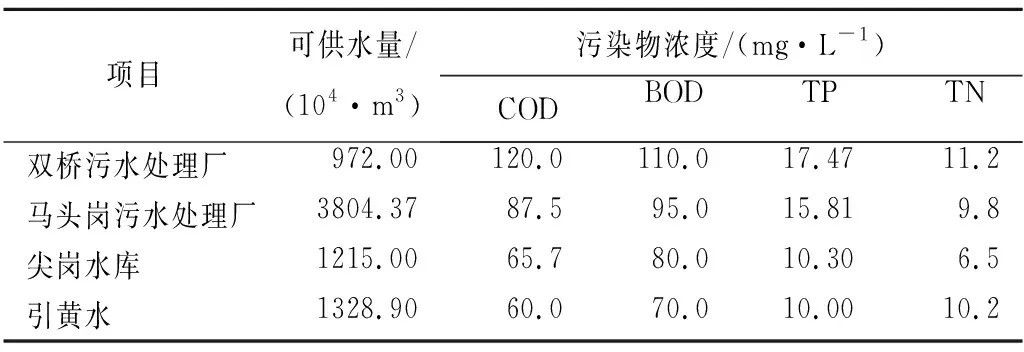
项目可供水量/(104·m3) 污染物浓度/(mg·L-1) COD BOD TP TN双桥污水处理厂972.00120.0110.017.4711.2马头岗污水处理厂3804.3787.595.015.819.8尖岗水库1215.0065.780.010.306.5引黄水1328.9060.070.010.0010.2

3.1.2 湖泊湿地运行调度方式分析

新开挖3处湖泊湿地与贾鲁河水体相连，湖泊湿地蓄水通过修建液压升降坝完成。根据《郑州市贾鲁河综合治理工程水资源论证报告书》(黄河水利委员会黄河水利科学研究院，2016年7月)[16]，贾鲁河生态用水年运行8个月(即1，2，3，4，5，10，11月和12月),共243 d。汛期(6～9月)停止运行。用水量只考虑每年10月至次年5月的用水。

贾鲁河生态运行期的换水。汛期过后需要进行首次充水，贾鲁河景观水体的充水量为1 557.30万m3，本文根据治理区域内污水处理厂以及3处湿地湖泊对应于河段的位置，将整个治理河段划分为5段。在计算过程中，假定治理河段内的污染负荷均匀、水力学特性和水文特征变化不大，再将每段河流进一步细分成河段长为1 km的计算单元，以此为基础，构建水环境管理模型。

3.2 贾鲁河水环境管理模型的构建

根据综合治理原则，污水处理运行费用最小和河流、湖泊、水库、水资源优化配置是模型构建的主要目标，而且以污染物消减率和河流、湖泊、水库的泄水量作为决策变量。

(1)

属于：

(1) 水质控制约束(COD,BOD,TN,TP)。

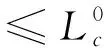
(2)

(3)

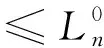
(4)

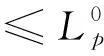
(5)

(2) 水库和河道放水约束。

O≤⊗(Qi)≤Qimax

(6)

(3) 供水能力约束。

⊗(Qi)≤Qdesign

(7)

(4) 污水处理效率约束。

0≤⊗(ηj)≤1

(8)

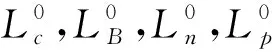
显然，改善污水处理厂的污染物消除效率会增加运行费用，同时会使其他水源的供水需求量减少。权衡污水处理厂的污染物消除效率和其他水源的利用量，是一项极具挑战性的工作。以合理的运行费用满足水质标准要求也是其中一项十分重要的工作。水环境管理模型的GA计算流程如图1所示。

3.3 遗传算法实现

3.3.1 灰色参数分析

模型解的合理区间选定，取决于对实际问题的识别与资料的可靠性[19]。本文涉及的灰色系统主要包括灰色响应矩阵U⊗a和灰色矢量m⊗矩阵，灰色响应矩阵U⊗a为污染物降解效率的函数，可以应用水质模型，采用推理法构建;灰色矢量m⊗可以直接通过调查样本来进行计算。这些灰色矩阵为构建灰色非线性规划模型、供水和污水处理效率方案提供了基础。

为了求解灰色非线性规划模型，需要构造2个能够反映非确定性影响的二级模型。其中，一个模型用于描述外部边界条件，另一个模型用于搜索优化解的下边界，这样可以彻底解决最终决策阶段的非确定性问题。

对于非线性模型，必须进行稳定性分析。因此，在任何情况下，GA解的过程总是可以保证灰色非线性规划模型的稳定性特征。

基于灰色最优解的目标函数推导出的灰色值，应该包括在灰色目标函数的区间内，这样才能在最终的决策过程中充分解决不确定性问题。从数学意义上来讲，可以严格证明这个灰色过程完全符合库恩-希尔斯(Kuhn-Tucker)拓扑要求的条件[20]。

本文涉及的灰参数名称、含义等、优化边界条件、约束条件等，见构建模型中各参数的说明[21-22]。

3.3.2 GA求解步骤

本文假定每个染色体代表整个群体中的一个独立解。染色体由二进制组合字符串组成[23]，代表污水处理厂的消除效率和不同水源的供水量。

虽然GA可以用来解决无约束的生产问题，该方法基于惩罚函数来代替约束条件，惩罚解超过一个系统给定的约束条件，因此，可以构造如下拟合函数。

Eval(Q,η)=

(9)

式中，α为惩罚系数,如果没有违反现象，惩罚为0，反之惩罚为正。在演变过程中,当评价函数解超过运行边界时， 说明染色体发育受到了严重影响，就很有可能被淘汰。

图2是水环境管理模型的GA的求解过程示意图。遗传运算持续进行,直到满足门槛值10-5(优化拟合值和平均拟合值之间的差值)。

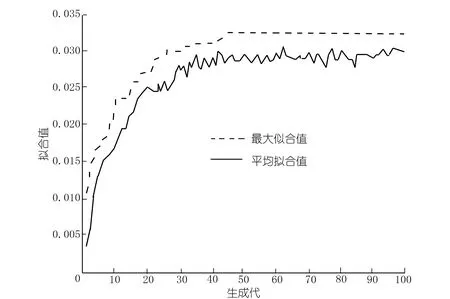
图2 GA算法拟合收敛过程Fig.2 Convergence of GA-based solution procedure(lower boundary)

4 计算结果与讨论

本文构建了贾鲁河灰色非线性模型，并利用GA算法和梯度非线性规划分别对水生态环境优化方案进行了求解。表2和表3分别为污水处理厂污染物消除效率和不同水源供水量的计算结果。

表2 GA算法和梯度非线性规划污水处理厂优化方案

Tab.2 Optimum schemes of WWTPs calculated using GA and Gradient-Based Nonlinear Programming

污水处理厂 遗传算法 消除效率/%优化费用/(万元·月-1) 梯度非线性规划 消除效率/%优化费用/(万元·月-1)双桥污水处理厂56.6417.0053.4611.3马头岗污水处理厂75.0578.7074.5749.0

表3 GA算法和梯度非线性规划供水量优化方案

Tab.3 Optimum schemes of amount of released water calculated using GA and Gradient-Based Nonlinear Programming

水源类型 遗传算法 供水方案/(万m3·d-1)优化费用/(万元·月-1) 梯度非线性规划 供水方案/(万m3·d-1)优化费用/(万元·月-1)尖岗水库14.00 12.00 15.4 15.3 引黄2.89 12.70 4.5 14.9

图3 GA和非线性规划法水质模拟结果
Fig.3 Water quality simulation results (GA and NP)

由表2和表3可见,运用GA算法计算得出的供水方案与运用梯度非线性规划法计算得出的结果非常接近。但是在保证生态环境用水的情况下,同梯度非线性规划法的计算结果进行对比,运用GA算法计算得出的方案结果是：尖岗水库可以节约水资源9.3%,可节约引黄水55.7%;同时,运行费用也有较大的节省,尖岗水库可减少运行费用39.6%,引黄水可减少运行费用17.3%。

为了检验GA算法的有效性,将GA算法与非线性规划方法的模拟结果进行了对比,对比情况如图3所示。

GA算法在初期阶段收敛速度快，当接近全域解时，收敛速度变缓，这对于渐进逼近算法来说是正常现象。计算结果说明，GA灰色非线性规划具有非常明显的潜力。

根据GA规划方案，应用一维水质模型，对每个河段的水质指标进行了计算，计算结果如图3所示。

由图3可见，GA算法的COD浓度位于水质标准的下边界，TN和TP的浓度均在下游河段较高。但是，在双桥污水处理厂排放后(两类污染物的浓度均超标的情况下，仍然低于2.0～0.2 mg/L)，运用梯度非线性规划计算得出的运行总费用高于GA算法计算出的总运行费，而利用GA算法计算得出的水质基本上与非线性规划算法计得出的结果相等。也就是说，GA是一个非常理想的优化算法。

5 结 论

(1) 本文研究结果证明了GA灰色非线性规划在水环境管理领域的应用具有十分明显的潜力。该方法可以合理处理水环境规划与管理中的不确定性问题，而且不涉及任何复杂的类似灰色拓展的数学运算；构建的模型简单，求解收敛速度快。

(2) 同传统方法对比，GA算法不需要线性化假设或辅助求解手段，避免了矩阵转换中数值的不稳定性，将GA快速搜索的优势成功地应用于模型求解，在短时间内即可以搜索到优化区间。可以肯定，GA算法对于解决非线性问题具有非常广阔的应用前景。

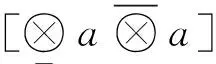
(4) 给出了灰色系统GA算法的求解步骤。本文假定每个染色体代表整个群体中的一个独立解，染色体由二进制组合字符串组成，代表污水处理厂的消除效率和不同水源的供水量。虽GA算法可以用来解决无约束的生产问题，但该方法基于惩罚函数来代替约束条件，惩罚解超过一个系统给定的约束条件，因此，本文构建了拟合函数，为灰色系统的求解提供了条件。

(5) 利用GA算法和梯度非线性规划，分别对水生态环境优化方案进行了求解。同梯度非线性规划法相比，GA算法得出的方案，可以使尖岗水库节约水资源9.3%，节约引黄水55.7%；同时，使运行费用也有较大的节省，尖岗水库可减少运行费用39.6%，引黄水可减少运行费用17.3%。

(6) GA算法的COD浓度位于水质标准的下边界，TN和TP浓度在下游河段较高，但是在双桥污水处理厂排放后(两类污染物的浓度均超标的情况下，仍然低于2.0～0.2 mg/L), 梯度非线性规划得出的运行总费用高于GA算法计算得出的总运行费，而利用GA算法得出的水质基本上与非线性规划算法计算得出的相等。也就是说，GA算法是一个非常理想的优化算法。