基于GA-BP神经网络的碾压混凝土压实度实时评价方法

2019-05-30田正宏苏伟豪焦新宸

水利水电科技进展 2019年3期

田正宏,苏伟豪,郑祥,焦新宸

(1.河海大学水利水电学院,江苏南京 210098; 2.中国水利水电第七工程局有限公司第一分局,四川彭山 620860)

碾压混凝土的施工质量对大坝结构安全至关重要。碾压施工时,每层压实密度是质量控制的核心指标[1]。因此,实时准确检测与评价仓面碾压压实密度是控制压实质量以及检测现场工艺是否合格的必要环节。目前,施工现场采用核子密度仪随机取点检测碾压层压实度[2]。这种方法效率较低,且单点人工测值结果表征性存在一定偏差,影响碾压层压实质量评价的客观性与准确性。此外,现有一些数字化碾压效果在线馈控方法基于先期试验仓的碾压遍数、设备参数、碾压速度、激振力等工艺参数构建实时评价模型[3-5]，但现场获取的相关工艺参数可靠性仍存在明显不足,如碾压设备的激振力[6]或加速度由于设备差异等复杂干扰而难以有效去噪,因而这类参数评价模型依旧不能很好地反映实时碾压密实性真实效果。鉴于此,本文基于可准确获取的仓面随机测点范围内碾前拌合料含湿率、碾压后表面应力波波速及相应碾压混凝土材料级配特征参数等,采用基于改进遗传算法的GA-BP神经网络(genetic algorithm-backpapagation artificial neutral network)构建压实度预测模型,实时预测仓面各检测点处的碾压混凝土压实度指标。

1 实时碾压压实度预测参数选择与获取

1.1 实时碾压压实度预测参数选择

为实现现场碾压施工质量的快速预测,选择合适可靠的实时检测模型参数至关重要。大量室内和现场试验及已有文献成果表明[7],影响碾压混凝土压实质量的主要因素为料性参数、碾压机械参数、温度、天气等。但是,在实际工程应用中,现场碾压机械参数、温度、天气等干扰因素复杂多变[8],实时采集数据的准确性难以控制和有效处理。因此,通过检测碾压后混凝土表面应力波以直接反映其内部结构特征,间接反映出了碾压机械参数、温度、天气等外部因素对碾压压实度的综合影响。另外,同一密实条件下碾压混凝土表面应力波波速稳定且波动范围小,而不同密实条件下表面应力波波速变化明显。相同碾压工况条件下,含湿率、级配和胶砂比作为料性参数表征碾压混凝土的可碾性,直接影响其压实度。因此,本文基于碾压工艺前后的料性特征的可靠获取性及处理方便的优点,选择含湿率、波速、级配因子和胶砂比4个影响因素,构建GA-BP神经网络预测模型,结合进一步的现场实时信息化施工[9]馈控系统,实现碾压混凝土压实质量实时、全仓面、精准化评价;对于现场欠碾压区域,通过增加碾压遍数等工艺调整,实现碾压质量的精细化控制。

1.1.1拌合料含湿率

新拌的超干硬性混凝土在振动碾压作用下,如果拌合料含湿率偏低,自由浆体不能充分填充拌合料孔隙,碾压层难以压实泛浆;反之,如果含湿率偏高,振动液化产生多余自由水,碾压能量部分消耗于超静孔隙水压力[10],内部颗粒受到的有效应力减少,也无法达到最佳压实度,因此存在一个合理含湿率以保证最佳压实度效果。鉴于此,将拌合料含湿率作为预测压实度指标的关键因素之一。

现有施工规范通常采用VC值法(维勃稠度法)表示拌合料的可碾性。但是现场施工过程,由于采用VC值法工作量大、时间长、步骤多以及人为因素影响较大等原因,事实上无法做到快速准确和连续多测点检测。已有试验研究表明,碾压混凝土的VC值与含湿率之间存在较密切线性相关性[11]。因此,采用拌合料含湿率替代VC值表征拌合料可碾性是可行的方法。

1.1.2碾压热层应力波波速

在半无限不均匀弹性介质中,横波与反射的纵波在自由表面处相互叠加和干涉,从而产生表面应力波。表面应力波在沿介质表面传播时,其能量主要集中在距表面大约一个波长的深度范围内。因此当碾压混凝土的密实度发生变化时,表面应力波在其内部的传播波速会随之发生变化;相同密实条件下碾压热层应力波波速稳定且波动范围小,即表面应力波对碾压施工层混凝土压实质量敏感性良好。鉴于此,本文将现场测试某一碾压工艺完成后的热层表面应力波波速作为另一个重要参数评价该层压实状态是较直接有效的方法。

1.1.3拌合料级配及胶砂比

碾压混凝土自身料性对压实状态有重要的影响,其中最主要的因素是粗骨料级配与胶砂比。碾压混凝土拌合料在振动液化后,骨料颗粒在重力和振动应力波的作用下向下运动、排列构成一个稳定骨架,粗骨料的级配状况和紧密程度将直接决定该骨架的空隙率和可碾性。这里定义级配因子λ衡量粗骨料级配情况:

(1)

式中:rs为骨料粒径为5～20 mm的质量分数;rm为骨料粒径在20～40 mm的质量分数;rl为骨料粒径在40～80 mm的质量分数;rz为骨料粒径在80～150 mm的质量分数。通过二、三级配以及全级配料不同配比的紧密密度试验,发现骨料级配因子与骨料紧密密度具有较强的非线性相关性(图1)。

图1 骨料级配因子与骨料紧密度的关系

从图1中可以看出,相同的振动能量输入时,骨料级配因子越大,振实空隙率随之增大,也即该级配的碾压混凝土越不容易压实;级配因子越小,振实空隙率越小,则该级配的碾压混凝土越容易压实。所以合理的级配有利于提高碾压压实度。

碾压混凝土的胶砂比代表配合比中胶凝材料含量。当胶砂比偏低时,振动液化产生的浆体变少,混凝土内部的空隙不能被浆液填充,导致无法振动压实,且碾压层表面无液化泛浆现象。当胶砂比偏大时,拌合物骨料颗粒周围的浆体层增厚,游离浆体增多,现场施工可碾性降低。因此将胶砂比作为表征碾压混凝土材料特性的定性指标,能够准确控制碾压混凝土的压实状态。

1.2 实时碾压压实度预测参数获取

1.2.1拌合料含湿率测定

现场碾压混凝土拌合料在运输、卸料、堆放和摊铺过程中,拌合物水分持续蒸发损失,进而导致拌合料含湿率降低。为此,要在仓面铺料后碾压前的短时间内检测现场碾压混凝土的含湿率。这段时间处于仓面喷湿小气候状态下,为提高测量效率和测量精度,拌合料的含湿率采用自主研发的含湿率测试仪直接测出。该测试仪根据电磁波在碾压混凝土中传播的频率来测试探针之间碾压混凝土相对介电常数[12],其计算公式为

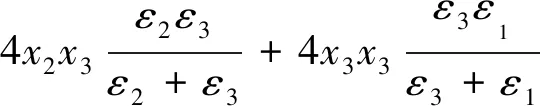
(2)

式中:ε为碾压混凝土介电常数;ε1、x1分别为空气的介电常数和体积分数;ε2、x2分别为砂、石、水泥、掺合料的介电常数和体积分数;ε3、x3分别为水的介电常数和体积分数。

含湿率测试仪根据相对介电常数与水的体积分数的关系,通过智能计算模块获取相应的电压值,计算出碾压混凝土的含湿率并输出。已有试验研究[11]表明,在VC值介于0～10 s时,粒径大于10 mm大骨料的表面含湿率变化对剩余拌合料影响很小,因此在现场试样测试前筛除粒径大于10 mm人工大骨料,以免大骨料的存在降低测试结果的精准度。将筛网筛过的细石混凝土分3次加入内径为11.0 cm、高为10.5 cm的筒状容器并捣实至表面泛浆;再将探针直接插入捣实的拌合料中进行测试(图2)。此外,在仓面施工碾压前实时测试时,每次累计筛料量应相差不多,且累计筛除时间大体相等;使用筛网取待测混凝土试筛,从而较准确地反映出碾压前铺摊料短时间内的料湿性状态。

图2 含湿率测试现场

1.2.2碾压层表面应力波波速获取

在半无限非均匀弹性介质中,表面应力波具有高度频散性,特别是距自由表面半波长的范围内。基于瞬态瑞雷波法[13]原理,采用专门研制的波速仪测出不同碾压密实状态下碾压层表面应力波波速(图3)。为防止因碾压层完工后间隙水化过程导致检测层强度、弹性模量等力学性能参数发生较明显改变,使检测波速发生较大的变化,进而影响压实度预测准确性,规定在每个碾压条带振动碾压结束后尽快完成波速测试。测试时,首先通过固定高度的小球自由下落冲击地面,在落地点激发具有一定频率带宽的混合频率表面波,波速仪2定点加速度传感器采集冲击后的瞬态表面应力波信号,通过傅里叶变化由时域转化为频域,经去噪过滤后,对频率为f的表面应力波分量通过互谱分析法,计算两个采集触点首波的相位差Δφ,由此得到碾压层表面应力波在该压实状态的平均传播速度:

(3)

式中:Δx为两个钢制触点的距离。为了保证应力波计算精度,Δx应满足:

(4)

图3 波速测试现场

2 GA-BP神经网络模型构建

遗传算法是一种具有全局搜索能力的概率性的自适应迭代算法,不受空间信息的限制。BP神经网络初始权值与阈值随机产生,极易陷入局部极值。因此采用遗传算法对BP神经网络的初始权值和阈值进行优化,在全局解空间多个区域内,寻找最优解或近似最优解。

2.1 BP神经网络模型

首先建立共M层、第m层神经元数为Sm的BP神经网络,随机产生一组权值wm,i,j与阈值bm，i,其中wm,i,j为第m层前一层的第j个神经元对当前层的第i个神经元的权值;bm，i为第m层的第i个神经元的阈值;m=1,2,…,M;i=1,2,…,Sm;j=1,2,…,Sm-1。

2.1.1信息的正向传递

对网络训练时,将输出值与目标值比较,然后调整相应的权值与阈值,以使均方差最小。根据LMS算法,输出层误差可以近似表示为:

(5)

式中:t(k)为第k次迭代时的目标变量矩阵;a(k)为第k次迭代时输出变量矩阵。

表1 大坝碾压混凝土配合比

2.1.2误差的反向传播

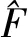
wm，i,j(k+1)=wm，i,j(k)+γ[wm，i,j(k)-

wm，i,j(k-1)]-α(1-γ)sm，iam-1，j

(6)

各阈值的修正为

bm，i(k+1)=bm，i(k)+γ[bm，i(k)-

bm，i(k-1)]-α(1-γ)sm，i

(7)

式中:sm，i为第m层的第i个神经元的敏感度;γ为势态因子,且0≤γ<1;α为学习速率。

2.2 GA-BP神经网络模型

2.2.1初始化种群

将网络中所有的权值和阈值直接采用实数编码的方式形成一组有序的基因串(二维矩阵)X=(wm，i,j,bm，i),基因串编码长度为

(8)

2.2.2适应度函数

鉴于遗传算法的搜索目标是寻找误差平方和最小的权值与阈值,因此第i个神经元基因串Xi的适应度函数采用误差平方和的倒数:

(9)

式中:aM，i，j为第i个基因串在输出层的第j个输出节点的输出值;ti，j为对应的目标值。

2.2.3种群进化

根据适应度函数将每个个体适应值由大到小进行排序,采用几何规划排序选择运算,得到上一代个体直接进入下一代的概率。然后从第l代种群中随机选择两个亲本Xl，i和Xl，j,采用算术交叉方式进行基因交叉,产生新个体由下式确定:

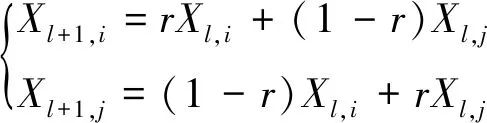
(10)

式中:Xl+1，i和Xl+1，j为交叉后的个体;r为[0,1]之间的随机数。

然后,采用实数编码下的非均匀变异算法,在子代中随机选择变异点k,若变异xk处的基因范围为[Lk，min,Lk，max] 则变异产生的新基因为

(11)

式中:r′为取值为0或1的随机数。

最后,应用BP算法对遗传算法优化权值W与阈值b进行精调,从而搜索出最优解或近似最优解。

3 实例验证

3.1 工程概况

乌弄龙水电站是澜沧江上游河段梯级开发的第二级水电站,为二等大(2)型水利工程,拦河大坝为碾压混凝土重力坝。以第1、2、3、4、5号坝段、第10仓为例进行测试。该仓面碾压混凝土拌合料使用P·MH42.5水泥和Ⅱ级粉煤灰;骨料采用砂石加工系统生产的人工骨料,母岩为灰岩,细骨料为灰岩人工砂,碾压砂细度模数为3.08,石粉含量(质量分数)为20.9%,其中小于0.08 mm微粒含量为6.8%,粗骨料经过砂石筛分系统二次筛分;外加剂采用ZB-1Rcc15、ZB-1A缓凝型高效减水剂和GK-9A引气剂;拌合水采用营地用水。碾压混凝土的配合比如表1所示。

3.2 压实度预测模型参数获取

现场采用含湿率测试仪直接测出仓面铺料后、碾压前拌合料含湿率;在振动碾碾压规定的遍数后,立即使用波速仪测定该位置表面应力波波速,同步采用核子密度计检测相应位置处的单点压实度。通过测定不同碾压层不同位置的含湿率、波速及压实度,结合已知的对应级配和材料胶砂比,建立1个500组样本的数据训练集。部分试验数据如表2所示。

表2 部分试验数据

以500组样本点数据作为训练样本,采用GA-BP神经网络进行训练。根据训练后的网络,预测随机选取的50个现场测试点压实度值,比较BP神经网络模型与GA-BP神经网络模型预测压实度的准确性与稳定性。

鉴于碾压混凝土的压实度与现场实际碾压料的含湿率、碾压层表面应力波速值、级配和胶砂比呈现复杂的非线性关系,尤其碾压层压实度还受碾压机械、温度、天气等外部因素影响,因而简单网络结构不易准确预测压实度,且稳定性较差。但网络结构过于复杂则将增加训练时间且易出现过拟合现象。因此采用1层输入层、2层隐含层、1层输出层,即1-2-1网络结构(图4)。2层隐含层神经元数分别为9和 4,其对应的传递函数分别为logsig和purelin,网络的学习速率为0.01。

图4 GA-BP神经网络结构

3.3 模型预测结果及应用分析

GA-BP 神经网络计算过程分为2个步骤。

第1步,采用遗传算法对BP神经网络的初始权值和阈值进行优化,设置种群数目为50,种群进化次数为100。在进化过程中,误差平方和与个体适应度随遗传代数的变化情况如图5、图6所示。经过约40代搜索后,误差平方和达到最小且趋于平稳。实际的适应度值在约60代进化后达到最大且趋于平稳。

图5 误差平方和进化曲线

图6 适应度进化曲线

第2步,采用BP神经网络算法对权值和阈值精细调节。在BP神经网络算法中,误差平方和在迭代600次左右时趋于稳定,迭代1 471次时停止。最后,分别采用GA-BP神经网络与BP神经网络对碾压混凝土压实度进行预测,结果如图7所示。

图7 基于BP与GA-BP神经网络的压实度预测

在50个预测点中,GA-BP神经网络模型的压实度预测值误差小于0.3%、0.6%和1%的样本比例分别为68%、83%及100%,BP神经网络模型的相应比例分别为32%、58%及82%;GA-BP神经网络模型预测值均方误差为0.137,最大误差为0.98%,BP神经网络模型预测值均方误差为0.499,最大误差为1.67%。GA-BP神经网络模型不仅预测精度更高,且偏差波动范围更小,能更准确有效地预测现场碾压层混凝土压实性。

GA-BP神经网络模型对碾压混凝土压实度下限值更敏感:压实度处于93%～96%的样本点,GA-BP模型预测值的平均误差为0.08%,最大误差为0.17%,误差很小;而压实度大于96%时,GA-BP模型给出的预测值平均误差在0.3%左右,最大误差分布约0.9%,且误差分布较为恒定。究其原因,预测误差与GA-BP网络模型结构有关:压实度低于96%的碾压测点,在高维空间数据离散性相对较小,由于模型算法具有较好的灵敏性和收敛一致性,因此拟合度高,预测精度高。这种特点对于现场施工中以某一合理压实度(如96%)作为合格碾压混凝土的最低评价指标,并以此判断压实效果的准确性十分有利。GA-BP模型更能准确判定不合格点数,有助于掌握多因素复杂条件的压实程度。

综上,基于GA-BP神经网络的现场实时压实度预测模型误差小、性能稳定,可用于碾压混凝土热层压实质量实时精准控制,对施工具有指导作用和实际应用价值。