非弃水期葛洲坝水电站下游水位变化过程预测新方法

徐 杨,樊启祥,尚毅梓,阮燕云,张玉柱,刘志武

(中国长江三峡集团公司,北京 100038)

葛洲坝水电站是三峡水电站的反调节电站,两者相距38 km,水力联系紧密,区间无较大支流汇入,三峡下泄流量基本等于葛洲坝入库流量。在实际调度过程中,若葛洲坝水电站上游水位控制出现偏差,仅能通过2种方式来调整水位:一是向电网申请修改发电计划;二是开启泄洪闸进行弃水。现实情况下,为保证电站效益和运行安全,弃水情况较少,非弃水期占全年运行期的80%以上。因此,非弃水期葛洲坝水电站下游水位的精准预测,对于编制葛洲坝水电站发电计划,提升发电效益具有十分重要的意义。

水电站下游水位受多种因素影响,尤其在承担调峰、调频任务时,电站出力和出库流量变化剧烈,会在下游河道形成水位、流速急剧变动的非恒定水流。这种下游水位的复杂变化不仅与当前的电站出力、上游水位等参数有关,还与以前的工作状态有关,即具有一定的“后效性”[1]。目前,葛洲坝水电站下游水位预测方法主要有水位流量曲线查值法与非恒定流经验公式法。水位流量曲线查值法原理简单,计算速度快,日常调度中应用最多,但存在以下不足:①所建立水位流量曲线是静态的,一般采用恒定流模式[2],当电站出库流量变化剧烈时,不能完全反映水流的动态过程,预测误差较大;②为保证水位流量关系曲线的单一性,一般选用电站日均出库流量与日均下游水位数据建立相关关系,而时段下游水位预测时直接采用基于日均数据建立的关系曲线,误差较大;③无法解决受多种因素影响的复杂水位预测问题,更无法解决电站下游水位变化的“后效性”等问题。非恒定流经验公式法是通过提出经验公式来反映水电站下游水位的不稳定波动。该方法计算速度快,一定程度上考虑了水位顶托、非恒定流等因素的影响,在复杂条件下的下游水位预测中,如流量变幅较大且受回水影响的条件下,较水位流量曲线查值法更为精确。然而非恒定流经验公式法是复杂下游水位变化关系的简单近似,无法对下游水位变化过程进行精确计算,且公式中参数率定依赖所选用的调度运行数据,具有一定局限性;日常调度应用中发现该方法存在适用性不强、计算结果稳定性不高等问题。

葛洲坝水电站作为世界上最大的低水头、大流量径流式水电站,电站调峰较大时,下游水位小时变幅可能超过1 m,累计变幅超过3 m,占电站额定水头18.6 m的16%,现用的2种下游水位预测方法均存在计算精度不高,无法有效对水位变化过程进行预测等问题。另外,水电站出库流量也存在计算误差,通过流量查算水位会带来误差累积等问题。因此实际调度中2种方法仅可用于对下游水位的初步估算。随着大数据战略的全面推进,数据挖掘技术不断延伸到各研究领域,一些学者采用神经网络(ANN)[3]建模的方法来解决受复杂条件影响的水位预测问题。神经网络是受生物大脑启发而设计的非线性复杂网络系统,其基本单元是节点,节点之间的连接方式通过学习不断优化。神经网络的通用性和强大性使其可以很好地解决大型和高度复杂的学习任务,是目前机器学习的最新趋势之一。将神经网络应用于水文序列的预测,可以不必预先确定样本数据的数学模型,仅通过学习样本数据即可挖掘出其中的隐含规律[4]。鉴于此,本文针对葛洲坝水电站非弃水期可直接测量读取的电站运行过程与下游水位变化过程数据,采用BP神经网络算法,建立了一种基于监控数据的水电站下游水位变化过程预测方法。该方法计算简单快捷,较现用方法预测精度提高较多,对水电站的调度运行具有重要的现实意义。

1 水电站下游水位预测方法

1.1 水位流量曲线查值法

该方法通过水电站历史日均出库流量与下游水位数据点绘制水位流量关系曲线或函数,然后根据曲线或函数,输入(时段或者日均)出库流量直接查算对应下游水位。

水电站下游水位计算公式为

Z=f(Q)

(1)

式中:Z为下游水位;Q为出库流量;f为下游水位与出库流量关系曲线或函数。

实际调度中发现用当前时段曲线查算下游水位的误差与之前时段的计算误差有关,为了提高精度,可采用前i日计算误差的平均值作为当日下游水位计算的误差修正值。

1.2 非恒定流经验公式法

该方法认为电站上游放水时下游水位涨幅与出库流量线性相关,闸门关闭时下游水位按指数规律消落[5]。若水电站较长时间没有工作,则下游将出现最低水位Z0。若让水电站增大出库流量一段时间,则下游将出现某一水位Zt,该水位与下游最低水位和出库流量有关[6]:

Zt=Z0+bQt

(2)

式中:Zt为增流后t时刻下游水位;Qt为t时刻电站出库流量;b为比例系数。

若某时刻后减去这一增大流量,下游水位将按与下游河谷特性有关的常数k指数规律消落:

Zt+ΔT=Z0+ΔZte-ΔT/k

(3)

式中:Zt+ΔT为减流历时ΔT后下游水位消落后的水位;ΔZt为减流前下游水位与最低水位Z0的差值。

引入符号a=e-ΔT/k,并将方程改为通用的形式如下:

Zt=Z0+aΔZt-1

(4)

式中:Zt为减流后t时刻下游水位;ΔZt-1为t-1时刻下游水位与最低水位Z0的差值。

若某一时刻又重新让水电站增大出库流量,则该时刻下游水位相对于Z0的偏离值由2个阶段的变幅之和决定,即

Zt=Z0+aΔZt-1+bQt

(5)

实际调度中,最低水位Z0和比例系数a、b可通过历史数据进行率定,然后输入出库流量以及上一时刻的下游水位,即可利用式(5)计算出水电站该时刻的下游水位。

1.3 基于监控数据的水电站非弃水期下游水位变化过程BP神经网络预测模型

1.3.1BP神经网络

BP神经网络模型是一种多层前馈网络模型,拓扑结构包括输入层、隐含层和输出层[7]。网络的学习分为正向传播过程和反向传播过程。正向传播的信号通过输入层经由隐含层,最终传到输出层。如果输出结果不满足期望误差,则进入反向传播,在反向传播中误差信号逆向传播并逐层修正各层神经元节点之间的阈值、权值,经过多次迭代,直至达到终止条件。

为避免电站出库流量的计算误差,本文选取可直接测量读取的电站运行与下游水位变化过程监控数据作为建模数据。当电站不发生弃水时,水库出库流量与当前时段的电站出力、上游水位、下游水位等相关[8-9];且下游水位回水顶托与电站该时段之前的出库流量及下游水位有关;同时,由于下游水位站点一般分布在库岸两侧,其水位变化也受分电站出力变化的影响。因此,本文将电站总出力、分电站出力、上游水位以及前期下游水位等电站运行状态作为下游水位变化的影响因素,构建预测模型。

模型的输入为:①前n小时内的逐小时电站总出力序列;②前n小时内的逐小时分电站出力序列;③前n小时内的逐小时上游水位序列;④前n-m小时内逐小时电站下游水位序列。模型的输出为:m小时内的逐小时电站下游水位序列(其中m∈n,n、m为自然数)。

1.3.2预测模型构建

设计BP神经网络时,需确定网络的拓扑结构,包括隐含层数、每层神经元数以及神经元的激活函数。此外,还需考虑数据的标准化、参数的初始化、模型训练的优化算法等。

a. 确定网络的拓扑结构。由于3层网络可模拟任意复杂的非线性问题,能够形成任意复杂区域[10]，因此,本文选用3层BP神经网络来构建水电站下游水位变化过程的预测模型,每层都包括若干个神经元,上下层之间的各神经元实现全连接,而同层之间的各神经元无连接。

激活函数能够为神经网络加入一些非线性因素,提高其解决复杂问题的能力。本文采用应用最广泛的tanh函数作为激活函数,以保证模型的输出在[-1,1]以内。确定隐含层神经元个数的常用方法是试探法[11]。本文将训练数据分为训练集和验证集,采用训练集训练模型,采用验证集验证模型的准确率。在对第1～16个隐含层神经元进行试探后,发现隐含层神经元个数为10时,验证集的误差最小,因此选择隐含层神经元个数为10。

b. 数据处理。由于选用的变量指标互不相同,且各变量指标的数量级差别较大,会对模型产生影响,因此在建模之前,需要对数据进行无量纲处理,减少因数据差异带来的误差。本文对输入输出数据进行如下归一化处理:

(6)

其中Ymax=1Ymin=-1

式中:Y为标准化之后的变量数据;X为原始数据;Xmax、Xmin分别为变量X的最大值、最小值。

c. 模型训练。在模型训练的优化算法方面,本文采用Levenberg-Marquardt优化算法,其收敛速度较快,精度较高,对于中等规模的网络来说是一种较优的训练算法。在MATLAB中,神经网络的Levenberg-Marquardt优化算法即为“trainlm”训练函数[12]。

d. 模型预测。将归一化后的输入、输出数据代入模型,采用梯度下降法进行训练,达到设定的终止条件后,保存训练好的模型。预测时,将预测数据归一化后代入模型,模型的输出结果按照下述公式进行反归一化处理:

(7)

2 3种预测方法在葛洲坝水电站中的应用

葛洲坝水电站分为大江电厂和二江电厂,两电厂被泄洪闸门分开,上游代表站水位为5号站水位,下游代表站水位为7号站水位。葛洲坝水电站装机23台,大江、二江、电源电站分别装机7、15、1台,设计装机容量为273.5万kW。葛洲坝水电站弃水时通常不参与系统调峰,不弃水时根据三峡出库流量和电网需求确定调峰容量。一般情况下,出库流量较小时,调峰量小于15万kW,机组无需开停机或开停机1～2台,下游水位变化不超过0.3 m;出库流量较大时,调峰量大于60万kW,机组开停机超过7台,下游水位变化可超过2 m。

分别采用现有方法和本文方法进行预测,分析葛洲坝水电站不弃水时,不同方法对下游水位的预测效果。选用2012—2014年数据进行模型构建和参数率定,2015年数据进行模型试验验证。

2.1 水位流量曲线查值法参数设置

2012—2014年葛洲坝水电站日均出库流量与7号站下游水位关系曲线如图1所示。采用二次多项式拟合的水位流量关系函数为

(8)

图1 葛洲坝日均出库流量与下游水位相关关系

式中:Z为葛洲坝水电站7号站下游水位;Q为葛洲坝水电站出库流量。计算采用前3日曲线查值计算误差的平均值作为当日下游水位计算的误差修正值。

2.2 非恒定流经验公式法参数设置

从2012—2014年葛洲坝2 h运行数据(流量数据2 h计算1次)中按流量分级选出典型过程,采用最小二乘法率定式(5)中参数a、b值，如表1所示。

表1 葛洲坝水电站非恒定流经验公式参数

注：Z0为7号站的下游水位

2.3 本文方法参数设置

由2012—2014年葛洲坝水电站1 h运行过程数据分析可知,电站出力变化后,下游水位大致在4～6 h达稳定状态,故将当前时段下游水位的前期影响时段定为6 h。初步试算并结合调度需求,将模型的有效预测时段定为6 h。因此,模型输入变量为:①前12 h的逐小时平均全厂总出力;②前12 h的逐小时二江电厂出力;③前12 h的逐小时5号站水位;④前12 h至前7 h的逐小时7号站水位。模型输出变量为剩余6 h的逐小时7号站水位。

对输入、输出变量数据归一化处理后,选用BP神经网络算法工具箱,设定隐含层神经元个数为10,最大迭代次数为10 000次,选择“trainlm”训练函数进行训练,训练精度为0.000 000 1。训练完成后,将模型输出结果进行反归一化处理,至此，非弃水期葛洲坝下游水位变化过程预测模型构建完毕。

3 预测结果对比分析

3.1 预测结果对比

2015年葛洲坝水电站不弃水时2 h预见期下游水位实测值及各方法预测误差对比见表2(由于葛洲坝出库流量2 h计算1次,故现有方法仅能做2 h预测)。

由表2可知,不弃水时3种方法均表现出低水位误差小,高水位误差大的现象,这是由于出库流量较小时,调峰量也较小,导致下游水位低,变幅小,预测相对准确;而出库流量较大时,调峰量一般也较大,此时下游水位较高,非恒定流现象明显,预测误差大。相比而言,基于监控数据的预测模型无论是对高/低水位或汛期/非汛期预测精度均较高,中位值稳定且较小,预测误差的绝对值最小。本文方法优于现用两种方法原因在于:低水位、小流量下,由于流量的计算误差,现用两种方法采用水位流量数据转换会使误差进一步放大,而本文方法在预测时直接读取电站出力计划曲线和控制方式,可以避免误差累积;高水位、大流量下,现用两种方法无法很好地解决非恒定流过程中水位流量存在的复杂绳套关系,而本文方法在建模过程中考虑多种因素的影响,精度更高。

表2 2015年葛洲坝水电站不弃水时下游水位3种方法预测误差对比 m

注:基于监控数据预测模型误差为1 h和2 h预测的平均值与7号站实际2 h平均水位之差。

结合表2、表3可知,葛洲坝水电站不弃水时,本文方法的逐小时水位过程预测精度也较高,其中低水位预测精度比高水位预测精度稍高,预见期6 h内最大预测误差绝对值均小于0.3 m。同时,随着预见期的增加,误差的均值和中位值在缓慢增加,但增加幅度不大,且误差的最大值、最小值并未随着预见期的增加而线性增加,说明该模型在预见期内预测误差无明显的过程累积效应,可一次进行准确的多时段序列预测。

表3 2015年基于监控数据预测模型的葛洲坝水电站不弃水时下游水位预测误差 m

总体看来,本文方法预测精度最高,曲线查值法和非恒定流经验公式法预测精度相当;同时,高水位、大调峰下,本文方法依然保持足够高的精度,而现有两种方法在下游水位超过43 m后,预测误差的绝对值基本大于0.5 m,最大绝对误差达1.114 m,占额定水头5%以上,严重影响该电站发电计划的制作精度。此外,本文方法延长了预见期,能实现下游水位逐小时变化过程(6 h)预测,且预测效果较好。

3.2 不同工况下的预测效果对比

2015年葛洲坝水电站调峰日数为320 d,年均调峰容量为30万kW左右,最小月均调峰容量为7万kW(1月),最大月均调峰容量为70万kW(7月)。本文针对汛期、非汛期,选择大调峰(80万kW左右),中调峰(30万kW左右),小调峰(10万kW左右)3种典型运行工况,共6种计算情景,对比分析3种方法的预测效果，见图2、图3。

图2 2015年(非汛期)葛洲坝水电站2 h平均下游水位预测过程与实际过程对比

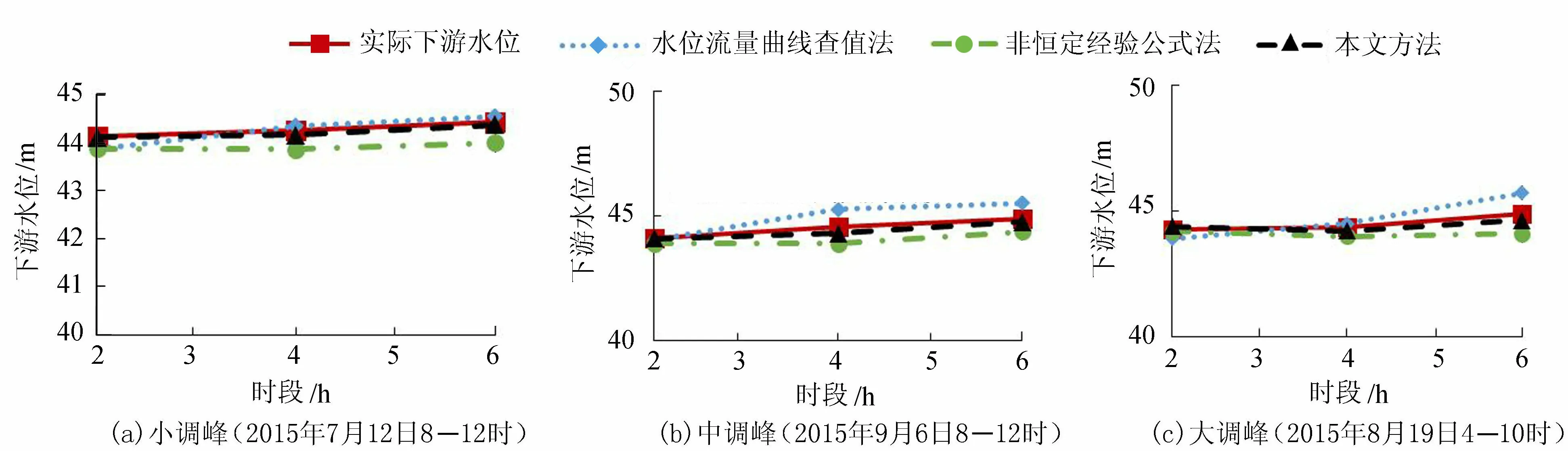
图3 2015年(汛期)葛洲坝水电站2 h平均下游水位预测过程与实际过程对比

由图2可知,随着调峰量的增加,现有方法的预测误差不断增加,而本文方法的预测误差变化不大,精度均较高且结果稳定。葛洲坝水电站汛期、非汛期小调峰下3种方法精度均较高,但现有两种方法预测误差的绝对值基本在0.3 m以内,本文方法预测误差的绝对值基本在0.1 m以内。葛洲坝水电站非汛期中等调峰下,现有两种方法的精度一般,预测误差的绝对值最大为0.45 m,非恒定流经验法较曲线查值法精度稍高,而本文方法的精度最高,预测误差的绝对值基本在0.2 m以内;而汛期中等调峰下,现有两种方法预测误差的绝对值最大均超过0.6 m。汛期、非汛期大调峰下现有两种方法预测误差的绝对值最大接近1 m,且预测结果不稳定,误差偏差范围大,而本文方法的精度依然较高,预测误差的绝对值基本在0.25 m以内。

总体来看,葛洲坝水电站调峰运行的典型工况下,本文方法精度最高,且计算结果稳定,非恒定流经验公式精度次之,曲线查值法精度低。对比现有两种方法,本文方法无论在预测精度还是预测频次方面均有大幅提高,葛洲坝水电站下游水位最大6 h变幅接近1.5 m时,该方法仍可快速准确地预测下游水位变化过程。

3.3 电量及上游水位控制偏差的累积效应分析

在实际调度中,非弃水期葛洲坝水电站需根据入库流量、电网下达的出力计划反算葛洲坝上游水位是否能按预定方案运行,若引起上游水位变化超出控制范围,则需重新计算发电计划,并向电网申请修改当前发电计划来控制上游水位。下游水位计算误差将影响发电水头的计算,使得水电站出力计算出现偏差;按此出力计划执行,将导致电站上游水位和电量预测存在偏差。另外,发电计划误差对电站上游水位和电量呈非线性累积的影响,例如葛洲坝下游水位预测值跟实际值相差0.5 m时,在发电流量18 000 m3/s、电站调峰30万kW左右的情况下,1 h时段末上游水位计算偏差将超过0.1 m,发电量计算偏差将超6万kW·h;2 h时段末上游水位计算偏差将超过0.3 m,发电量计算偏差将超15万kW·h。本文将以上文设定的葛洲坝水电站非汛期、汛期,调峰小、中、大工况的实际上游水位和电量作为基准,采用现有方法与本文方法连续预测未来6 h下游水位过程,反算电站发电量和时段末上游水位,并与基准对比,分析不同方法对电量和上游水位的累积影响，见表4、表5。

表42015年不同工况6h内电量偏差对比万kW·h

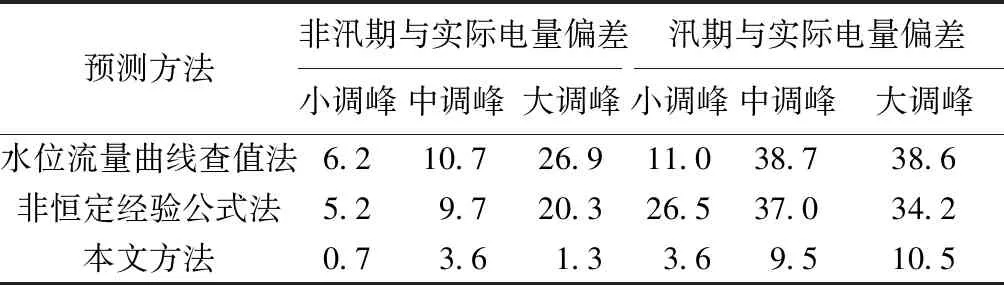
预测方法非汛期与实际电量偏差汛期与实际电量偏差小调峰中调峰大调峰小调峰 中调峰大调峰水位流量曲线查值法6.210.726.911.0 38.738.6非恒定经验公式法5.29.720.326.5 37.034.2本文方法0.73.61.33.6 9.510.5

表5 2015年不同工况预测6 h末上游水位控制累积偏差对比 m

由表4、表5可知,随着调峰量的增加,现有方法计算的电量偏差和上游水位控制累积偏差也不断增加,且上游水位控制累积偏差呈指数增长状态,即前期水位计算误差将对后期水位计算造成巨大影响;而本文方法的预测精度随调峰量的增加偏差变化不大,计算结果稳定,误差最小。水位流量曲线查值法6 h电量累积偏差最大达38.7万kW·h,上游水位控制累积偏差最大达0.33 m,而本文方法6 h电量累积偏差最大仅为10.5万kW·h,上游水位控制累积偏差最大仅为0.10 m,无论在电量计算还是水位控制精度均有大幅提高,有力地保障了电站效益和安全运行。

4 结 论

a. 非弃水期水电站下游水位的变化过程受多种因素影响,本文针对现有方法水位预测误差较大的情况,提出利用BP神经网络算法模拟电站运行过程与下游水位变化过程之间的关系,建立了基于监控数据的水电站下游水位变化过程预测模型。实际应用表明预测模型计算精度较高,该方法可以直接用于生产调度实践。

b. 基于数据挖掘原理的BP神经网络模型预测效果较好,尤其针对运行时间长、资料详实的日调节或径流式电站,如葛洲坝水电站。其原因在于径流式电站运行水位变幅小,且电站运行时间长,数据多,建模时输入数据中已包含各种工况,因此模型预测效果好。实际应用表明模型预见期内最大预测误差的绝对值小于0.25 m。

c. 本文提出的预测方法还有其他方法不可比拟的优势，譬如：可实现通过监控数据中直接测量的电站运行数据和下达的发电计划数据直接预测下游水位变化过程；可进行计算时段为1 h的水电站下游水位连续过程预测,较现有方法计算结果稳定,同时避免了现有方法预测过程的误差累积;计算时间短,计算精度较高。然而,BP神经网络模型的应用需水电站拥有多年详实的监测运行数据,在后期研究中可进一步分析缺少资料条件下的BP神经网络建模。