基于ECT/EST双模信息融合的磨粒图像重建算法*

(1.中国民航大学电子信息与自动化学院 天津 300300；2.国家电网天津市电力公司 天津 300010)

发动机在工作过程中，内部必然会出现摩擦损伤，产生大量磨损颗粒。及时了解滑油中的磨粒信息，可以有效监测发动机的磨损状况，对发动机的故障诊断具有重要意义。针对润滑油中磨粒的在线监测，国外起步较早，主要围绕电学类方法进行研究，并进行了摩擦磨损实验，得到了研究故障诊断的一些实际数据。国内主要围绕声、光技术和电荷技术和新工艺技术等方面，对润滑油中磨粒的监测方法进行了研究[1]。

电容层析成像(Electric Capacitance Tomography，ECT)技术，通过测量管道周围传感器电极对间的电容值，得到管内的介电常数分布，然后反演出管内的各相分布信息。因其具有非侵入、响应速度快、安全性高及成本低等优势[2-4]，ECT技术在多相流检测方面获得了广泛应用，但在发动机油路实时监测中，因摩擦产生的能量释放使得磨粒上积累了大量的电荷[5]，根据带电颗粒的静电感应原理，ECT传感器的电极上会感生出一定的电荷量，此电荷量会对ECT传感器电容值的测量产生影响，进而影响成像质量。GAO等[6]针对荷电颗粒对ECT的影响做了一些研究，通过仿真和实验得出，离电极比较近的荷电颗粒对ECT的影响，远大于距离比较远的荷电颗粒对ECT的影响。ZHANG等[7]研究发现，当静电荷引入到气力传输系统时，ECT的成像质量将下降。

电荷层析成像(Electrostatic Tomography，EST)技术，是基于阵列式静电传感器对荷电颗粒的感应，实现对流动颗粒分布图像重建的技术。相对其他电学层析成像技术，EST技术所需要的电路更简单、响应速度更快[8-9]，因此可以利用EST技术获得两相流中固体颗粒的信息。针对荷电颗粒对ECT电容值测量的干扰， LI等[10]在气固两相流的研究中，通过研究ECT电容检测电路，提出一个改进的电容检测电路，移除叠加在电容信号上的静电信号。周宾等人[11]将EST与ECT 2种模态进行融合，同时获取介质分布和电荷分布，由ECT提供的介质分布信息修正实际流型下的EST电荷灵敏度，从而改进EST图像重建质量。在ECT/EST双模信息融合应用于多相流图像重建方面，文献[12-13]将ECT的数据作为先验信息应用到EST的图像重建中，获取了气固两相流中的固体颗粒信息，结果表明，ECT获得的介电常数分布可用于提高建立EST电荷敏感场的迭代精度，从而降低电荷分布反演计算的不确定度。

本文作者针对荷电磨粒对ECT电容测量值的影响，提出一种ECT与EST融合的双模态传感器系统，以及基于双模信息融合的成像方法。该方法利用EST提供的荷电磨粒信息对ECT中畸变的电容值进行修正，然后用修正后的电容值进行图像重建，提高了图像重建质量。

1 ECT与EST融合的双模态传感器

1.1 传感器结构

图1所示为ECT与EST融合的双模态传感器结构示意图，其由一段长20 mm，内径为10 mm的绝缘管， 8个矩形测量电极和8个屏蔽电极，再加外围一个屏蔽罩组成。8个测量电极和8个屏蔽电极组成一个环状阵列，测量电极紧贴在绝缘管道外表面，屏蔽电极在2个测量电极之间，部分嵌入到绝缘管道壁，外部为屏蔽罩。因为传感器的结构参数决定电极上的感应电荷和对应灵敏场的分布，灵敏场的分布又决定着图像的重建质量，以管道内的灵敏度均匀性最佳为目标对传感器结构进行优化，通过仿真实验对比最佳电极覆盖角，进而确定传感器电极个数[14]。该模型电极覆盖角弧度为0.818 0，对应电极个数为8个。

图1 传感器结构图

1.2 数学模型

EST系统中电极上的感应电荷量表示形式如下：

Q=∫sD(x,y,z)ds

(1)

式中：s为传感器上每个感应电极的表面积；D(x,y,z)为s上的电位移矢量。

ECT系统中激励电极和测量电极之间的电容可以表示为

C=QU=-1U∫∫τε(x,y)u(x,y)dτ

(2)

式中：U为激励电极与测量电极之间的电压;ε(x,y)为场域内的介电常数;u(x,y)为电位;τ为电极的表面积。

2 双模态信息融合方法

多模态信息融合技术是通过一定的算法实现多个信息源的数据“合并”，以产生更可靠、更精确的信息，即根据多源观测信息给出一个关于状态的最优估计量[15-20]。在多传感器融合系统中，可以利用信息

融合的方式降低不利因素对系统的干扰，提高系统的稳定性。在润滑油管道中对ECT/EST双模态信息进行融合，利用EST传感器得到的电荷量修正ECT传感器得到的电容值，降低管道中荷电颗粒对ECT传感器电容值测量的干扰，提高系统的稳定性。

ECT/EST双模态信息融合采用的是特征级融合，将2个传感器的观测信息进行特征提取，然后将提取的信息进行融合，即用EST的观测信息修正ECT的观测信息。

在EST系统中，当荷电颗粒通过金属电极组成的传感器阵列时，传感器阵列的每个电极上都会产生感应电荷Qi,i=1，2,......,8。

在ECT系统中，依次在每个极板上施加激励电压，测量该激励电极与其余极板所构成的两端子电容值。对于N个极板构成的成像系统，独立测量的电容值数为C2N=N(N-1)/2。文中双模态传感器有8个电极，则得到28个电容值Cij(j= 1，2，......，8，i≠j)，表示第i个电极与第j个极板所构成的两端子电容值。

仿真实验发现，将荷电颗粒靠近管壁且邻近第4和5号电极时，对应的第3、4、9、10、14、15和19个电容值出现比较大的畸变。可以推断出，当荷电颗粒靠近某电极时，且以此电极为测量电极的电极对间的电容值发生较大的畸变。在ECT系统中，相邻电极对间的电容值呈对称分布，当荷电颗粒存在时，与颗粒距离不同的测量电极对应的电容值受干扰程度不同，从而电容值的对称性分布遭到破坏。在相同情况下利用EST系统获得磨粒信息，发现第4、5号电极上的感应电量最大，可以推断出EST电极上的感应电荷量的大小与ECT中电容值的畸变程度成正比。

基于加权融合方法修正ECT模态测的电容值：分配权重因子时，畸变的电容值给予较小的权重，以减弱畸变值在逆问题中的贡献率。因为EST电极上的感应电荷量的大小与ECT中电容值的畸变程度成正比，所以结合EST系统的信息，以电极上感应电量的倒数作为权重因子与电容值相乘，然后将加权后同一激励电极对应的电容值进行求和提取特征值得到一组特征向量Pn(n=1,2,......,7)。因为相邻电极对间的电容值是对称分布的，但荷电颗粒对不同电极对间的电容值测量的干扰是不一致的，所以电容值的“U”形曲线遭到破坏。为了进一步修正受干扰的测量值，最后将特征向量以仿真实验中空场对应的各电容值比例因子进行反投影，使相邻电极对间的电容值偏向对称分布，进一步减弱荷电颗粒对ECT的干扰。得到一组28×1的向量C′ij，即修正后的电容值。

修正方法步骤如图2所示。

图2 修正算法步骤

将ECT传感器的一组测量数据，与双模态传感器修正值进行对比，如图3所示。

图3 测量数据和修正结果对比

从图3中可以看出，使用加权融合的修正方法的双模态传感器得到的电容测量值，U形曲线更加规律，没有大的病态性波动，能够有效降低荷电颗粒存在的情况下ECT传感器受干扰的程度。

3 实验验证

利用COMSOL Multiphysics 5.3多物理场仿真软件结合MATLAB 2014a平台进行仿真实验，计算机配置为3.31GHz Intel Core i5处理器。建立传感器模型如图4所示，管道长为20 mm，内径为10 mm。利用场域内的一个点模拟润滑油中的荷电磨粒，电极覆盖角为40°，轴向长度为10 mm。在管道内稀相流中颗粒密度小，且被润滑油泡包裹，电极上的感应电荷量很微小。仿真实验中设置颗粒电荷量为1×10-13C。敏感场内设置的介质为润滑油，相对介电常数设为3.5，空气的相对介电常数设置为1。物理场设置中，电极上的激励电压为1 V。

图4 传感器模型图

3.1 ECT成像实验

为了验证荷电颗粒对ECT传感器电容值测量结果的影响，实验模拟了两相流中的3种经典流型——环流、泡状流、核心流。利用Tikhonov正则化图像重建算法对管内的各相分布信息进行图像重建，结果如表1 所示。

表1 ECT图像重建结果

由表1所示实验结果可见：在荷电颗粒位于几何中心的情况下，荷电颗粒对ECT传感器的影响可以忽略；当荷电颗粒越靠近电极时，成像结果越差，即测得的电容值畸变程度越强烈，图形重建结果越差。

3.2 ECT、EST双模融合成像实验

根据静电感应原理，荷电颗粒离绝缘管道外部的测量电极越近，对应电极上的感应电荷量越大，这与ECT系统中荷电颗粒对电容值测量的干扰是成正比例关系的，即测量电极上的感应电荷量越大，对应的电极对间的电容值畸变程度越大。所以利用加权融合的修正方法修正ECT测得的畸变电容值，减弱荷电颗粒对ECT电容值测量的影响。

为验证双模态系统图像重建效果，利用ECT系统对3个流型进行实验，并且利用点电荷模拟荷电颗粒放置在3个流型的不同位置(分别是：1个颗粒时放置在(0,3,0)，2个颗粒时分别放置在(0,3,0)、(0,-3,0)，3个颗粒时分别放置在(0,3,0)、(0,-3,0)和(3,0,0))，做了对比试验。实验结果如表2所示。

表2 双模态图像重建结果

由表2可见：ECT与EST融合的双模态传感器成像效果明显好于单个ECT传感器成像效果；由双模态重建图像可正确识别流型，荷电颗粒对ECT电容值测量的影响也有了明显改善。

3.3 实验结果分析

利用图像误差(Image Error,IME)和图像相关系数(Correlation Coefficient,CORR)[21]，对ECT传感器的图像重建效果和双模态传感器的图像重建效果进行定量分析。

图像误差(IME)定义为

εIME=‖G-G‖‖G‖

(3)

图像相关系数(CORR)定义为

rCORR=Σmi=1(G⌒i-G⌒)(Gi-G)Σmi=1(G⌒i-G⌒)2Σmi=1(G⌒i-G)

(4)

式中：G为模型设定中的介电常数分布;G⌒i为图像重建的介电常数分布;G、G⌒分别为G和G⌒的平均值。

εIME的值越小，rCORR的值越大，说明图像重建质量越好。

根据式(3)、(4)计算出图3所示双模态传感器和ECT传感器，在不同流型及不同荷电颗粒存在的情况下的重建图像的εIME和rCORR，结果如表3所示。

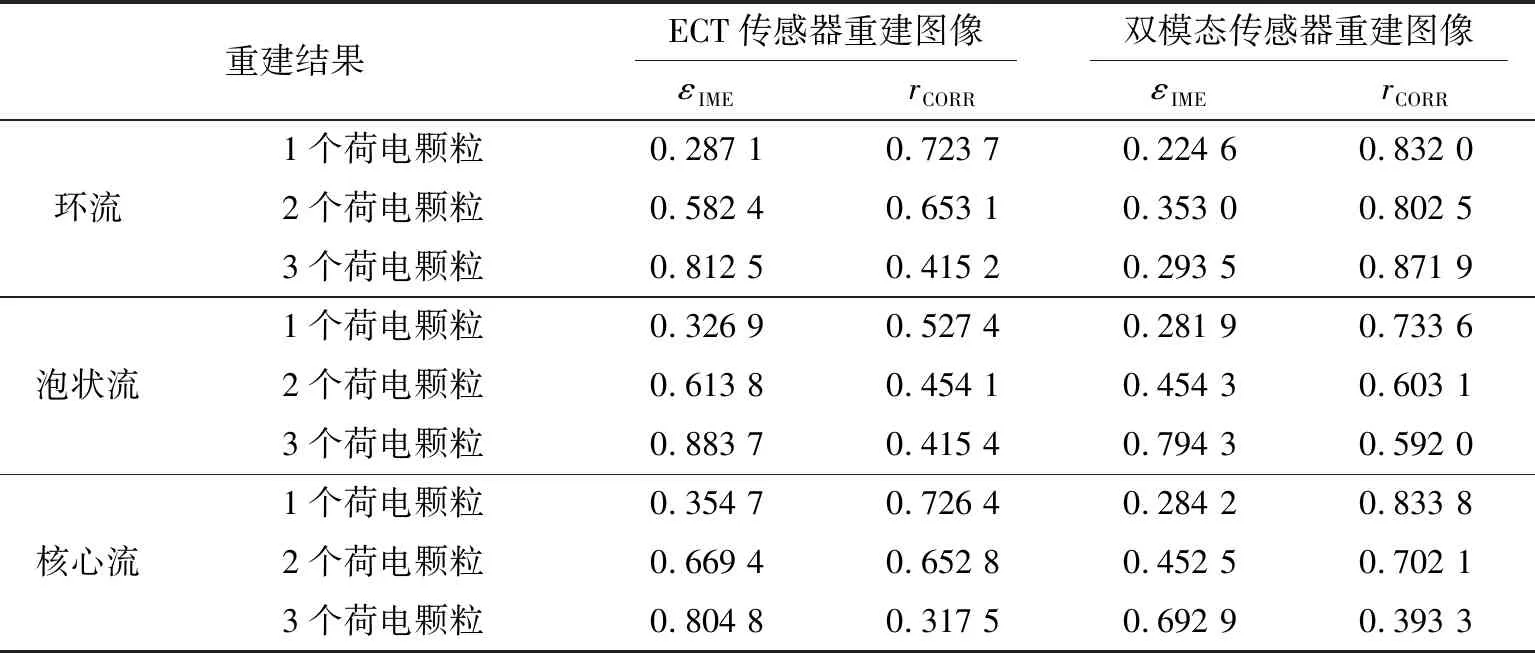
表3 图像重建结果误差和相关系数

根据表3可以看出：双模态传感器重建图像的误差相比ECT传感器的重建图像误差，在各种流型下都有显著的降低；在相同的流型下，双模态传感器重建图像的相关系数更高。所以，在荷电颗粒存在的情况下，将ECT传感器与EST传感器进行融合，修正受荷电颗粒影响的电容值，能够有效地提高ECT传感器的图像重建质量。

4 结论

提出ECT与EST融合的双模态传感器，利用EST系统测得的磨粒电荷信息对ECT系统中受荷电颗粒影响的畸变电容值进行修正，降低了荷电磨粒对ECT传感器电容值测量的影响，提高了系统的稳定性，仿真实验表明该方法重建的图像质量相对于单一ECT模态的成像质量有一定提高，由图像可有效识别环状流、泡状流、核心流等几种典型流型。为ECT、EST双模融合系统在油液在线监测中的应用提供了研究基础，在此基础上可对EST测量数据进行深入分析以期获得更准确的磨粒荷电信息，进一步提高监测精度。