受压弯剪型开孔芯材屈曲约束支撑试验
2019-05-29贾良玖董洋
贾良玖 董洋


摘 要:提出一种芯材开孔的新型全钢屈曲约束支撑,简称为PBRB.该支撑由开孔平板芯材,填充板及盖板通过螺栓连接而成.通过3根芯材具有不同开孔形式的PBRB试件的拟静力试验和相关数值分析,重点考察了芯材开孔形式对PBRB抗震性能的影响.研究结果表明:PBRB具有滞回性能稳定、延性高及累积耗能能力优良等特点;开孔芯材受压变形为压缩、剪切与弯曲组合的机制;开孔芯材“短柱”的长细比是影响PBRB性能的关键参数,芯材“短柱”长细比过大会造成PBRB滞回性能相对较差,基于试验结果给出了偏保守的设计长细比限制;同时提出了PBRB初始刚度的计算方法,评估精度良好.
关键词:屈曲约束支撑;开孔;剪切;全钢制;滞回
中图分类号:TU391 文献标志码:A
Abstract:A novel type of steel buckling-restrained braces (BRBs) is proposed, in which the core plate is perforated, termed as PBRB. PBRB is composed of a perforated core plate, 2 filling plates and restraining plates, which are assembled by bolts. Quasi-static cyclic tests and the corresponding numerical analyses were carried out on 3 specimens with different configurations of holes, the effect of which on the seismic performance was investigated emphatically. It was showed that PBRBs had stable hysteretic properties, high ductility and energy dissipation capacity. The compressive deformation of perforated core plates was found to be composed of compression, shear and flexural deformation. The slenderness ratio of "stub columns" is a critical parameter that affects seismic performance of PBRBs. An oversized slenderness ratio can lead to relatively poor seismic performance. A conservative design limit for the slenderness ratio was proposed based on the experimental results. A method with good accuracy has been proposed to evaluate initial stiffness of PBRBs.
Key words:buckling restrained brace;perforated;shear;all-steel;cyclic
支撐作为主要的抗侧力构件之一,可以有效地提升框架结构的侧向刚度.在中震和强震时,传统有支撑框架中的钢支撑会出现受压屈曲,受压侧的承载能力迅速退化,其耗能能力相比失稳前大幅降低.相对于传统支撑,学者们提出了一种能够防止受压屈曲变形过大的新型支撑,即屈曲约束支撑(BRB).BRB能够有效提升板件失稳后的受压承载力,进而提高支撑的耗能能力.BRB具有滞回性能稳定,减震耗能效果显著等特点,目前被广泛应用于抗震要求较高的结构中.BRB通常由以下5个部分构成:约束屈服段、约束非屈服段、无约束非屈服段、无粘结材料以及屈曲约束组件[1].BRB的相关研究最早可以追溯到20世纪70年代,由日本学者最早提出并进行了一系列试验和理论研究[2].在北岭地震、神户地震和集集地震之后,美国、日本、中国台湾等地震多发国家及地区对这种具有优异耗能性能的构件进行了大量研究,开发出种类繁多的产品并投入实际工程使用[3].
尽管目前BRB形式多样,但其工作原理基本相似,即通过屈曲约束组件防止内部金属芯材受压时发生过大的面内和面外变形,进而通过芯材的金属滞回塑性进行耗能,也可视作金属阻尼器[4-5]的一种.在以往的研究中,BRB的屈曲约束组件通常采用填充砂浆的钢管.与钢管填充砂浆屈曲约束支撑相比,全钢制屈曲约束支撑自重更小,且其生产质量更容易得到保证[6].此外,由于不需要像钢管填充砂浆屈曲约束支撑那样需要等到砂浆硬化才能进行施工安装,全钢制屈曲约束支撑可以缩短制作周期,加快施工进度.Haginoya等人提出一种开孔三管BRB[7],其中两个管作为约束组件被用来限制中间开孔管的屈曲变形,试验表明这种由低屈服点钢制作的开孔三管BRB具有稳定的滞回性能和良好的抗震性能.广州大学周云等、邓雪松等提出了一种开孔屈曲约束支撑,并进行了试验研究,试验结果验证了开孔屈曲约束支撑稳定的滞回性能和良好的耗能能力[8-9].本文基于缀板柱的设计思想提出一种新型开孔全钢制BRB(本文简称PBRB),与之前研究者提出的BRB不同之处在于其受压阶段芯材的新型变形机制.普通BRB的芯材随着压力增大,长度随之缩短,在屈曲约束组件约束作用下出现高阶多波屈曲模态,其压缩变形主要由芯材整体弯曲变形贡献.本文所提出的PBRB在压力作用下,在出现上述变形模式的同时开孔芯材处还会发生类似于受压格构柱的剪切变形等其它变形机制,其受压变形机制为弯剪型.众所周知,金属的剪切变形性能一般较稳定,具有剪切变形新机制的BRB相关研究对于BRB性能的提升以及新型高性能金属耗能产品的开发和应用意义重大.同时,本研究通过特殊的节点构造设计,有效避免了PBRB节点处受压时发生过早的屈曲或者节点焊缝超低周疲劳破坏.试验考察了不同开孔设计对于PBRB滞回性能的影响,试验结果显示本文提出的PBRB具有稳定的滞回性能和累积塑性耗能能力,同时开孔设计减缓了由于摩擦而造成的受压强度过度上升现象.
1 设计思路
如图1所示,PBRB主要由以下几个组件构成:1)1块通长开有类椭圆孔的平钢板芯材;2)2块盖板,用来限制芯材发生平面外过大变形;3)无粘结材料;4)2块比芯材稍厚的填充板,通过厚度差形成芯材与盖板之间的间隙,在约束芯材平面内变形同时,也不会由于芯材受压时的泊松效应而产生过大的约束应力.此外,填充板之间的宽度也比芯材的宽度大2 mm,其设计意图与上述类似.
PBRB的芯材通过开孔削弱了耗能段的截面强度,使芯材在地震荷载下可以快速屈服,尽快进入耗能,提高耗能效率.其次,芯材的屈服依次发生在局部削弱部位和非开孔部分,使得支撑可以分阶段进入塑性耗能,提高了屈曲约束支撑的屈服后二阶刚度,这有利于减小屈曲约束支撑的残余变形.此外,芯材通过开孔削弱了耗能段的极限承载力,有利于减轻节点的压力,从而可以使得节点的设计强度可以有所下降,不必像普通BRB那样对节点进行大幅加强.
传统BRB在受压侧的变形主要是由芯材高阶屈曲模态引起的,平面内和平面外的整体屈曲都会导致芯材长度的缩短.因此,普通BRB受压侧的变形机制主要是芯材的轴向压缩变形、平面内和平面外弯曲变形.PBRB的变形机制则和普通BRB不同,其受压时的变形机理与缀板式格构柱类似,芯材的压缩变形包含轴向压缩变形、整体平面内外的弯曲变形和剪切变形等变形机制.如图1所示,芯材沿长度方向均匀开孔,孔之间用“短桥”连接.“短桥”与格构柱中的缀板功能类似,保证不同单肢之间的共同工作.芯材的开孔采用了长条形类椭圆孔,中间为长方形,两端为半圆形,这样的设计细节是为了尽量减小局部应变集中,以防止试件在孔端因应变集中发生过早的破坏.开孔将芯材分为多个单肢“短柱”,PBRB不仅会发生芯材的整体屈曲,也可能发生“短柱”的单肢失稳,单肢的性能对于PBRB的整体性能具有重要影响.同时,由于芯材中心部分的削弱,导致PBRB芯材的轴向刚度要小于相同尺寸普通的平板芯材.
2 试验方案
2.1 试件尺寸及构造
本研究共设计了3个PBRB试件,芯材分别采用不同的开孔模式:分别称为单排孔,两排孔和三排孔试件.除了孔洞横向布置不同,芯材几何尺寸,孔洞的形状、大小及纵向孔间距均相同,如图1(a)(b)(c)所示.填充板和盖板的几何尺寸及构造如图1(d)(e)所示.芯材、填充板和盖板的厚度分別为10 mm、12 mm和14 mm.所有相同厚度的组件均加工自同一块钢板,以尽量避免材料离散性的影响.芯材中部设置一对防滑块,用来防止芯材与盖板之间发生相对刚体位移.3个试件的塑性变形段长度相同,均为670 mm.在试件的两端分别各焊接两个加劲肋以提高端部的平面外刚度,防止在端部的连接处出现局部失稳.盖板与填充板之间通过高强螺栓连接,在平面内和平面外方向,组件间的间隙尺寸均为1 mm,以限制芯材在压力作用下产生过大的屈曲变形.
2.2 材性试验
PBRB芯材均由结构钢SS400加工而成,材性试件几何尺寸如图2所示,试件均取自钢板轧制方向.由材性试件所得的工程应力-工程应变曲线如图3所示,引伸计标距为200 mm.
2.3 试验装置及加载历史试验采用MTS疲劳试验机,设备加载能力为500 kN,行程为±75 mm.试件两端由液压夹头夹紧,上端夹头可移动,底端夹头固定,试验装置如图4所示.试验中,共使用6个LVDT位移计,每2个位移计一组,分别测量PBRB盖板、固定端和可移动端的变形或位移.试验的加载历史为如图5所示的渐增滞回加载,每半圈位移增量为0.5%的芯材平均应变,在本试验中为3.35 mm.3个试件均采用此种加载制度,通过PBRB上下端位移差控制加载,试验为拟静力加载,试验温度为室温.
3 试验结果分析
3.1 滞回性能3个PBRB试件的平均应力-平均应变曲线如图6所示,其中横轴代表平均应变,由芯材净位移除以塑性变形长度得出,在本试验中塑性变形长度为670 mm;纵轴代表平均应力,由轴向力除以芯材最小截面积得到.
图6显示单排孔和两排孔试件的滞回曲线饱满且光滑,最大平均应变可以达到5%;三排孔试件的滞回性能明显不如单排孔和两排孔试件,但滞回曲线形状饱满,最大平均应变也可以达到3%,表明PBRB试件具有良好的延性和耗能能力.单排孔和两排孔试件均在-5%~+6%受拉半圈发生延性断裂破坏,三排孔试件在-3%~+4%受拉半圈发生破坏.在相同的加载制度下,单排孔和两排孔试件的变形能力比作者之前提出的高性能鱼骨形BRB[6]大.而一般的BRB达到3%即可被称为高性能BRB.需要注意的是,由于普通BRB压缩时的高阶弯曲变形,伸长率超过25%的钢材也较难达到3%的变形能力.图6显示三排孔试件与其它两个试件相比,在受压侧具有更加明显的应力波动;两排孔试件受压侧的应力波动比单排孔试件要大,这种现象是由芯材受压屈曲后与盖板和填充板接触导致的.随着开孔数增多,芯材开孔处的“短柱”长细比增大,更容易发生弹塑
(a)单排孔试件
(b)两排孔试件
(c)三排孔试件
(d)3个试件对比性失稳,试件的受压侧应力波动随之增大.3个试件的最大抗压强度Cmax、最大抗拉强度Tmax和屈服强度Ty均在表1列出.3个试件的拉压强度比(最大抗压与抗拉强度的比值)分别为1.19、1.3和1.23,强化系数(最大抗拉强度与屈服强度之比)分别为1.45、1.5和1.45.基于以上讨论可得出以下结论:在滞回加载过程中,PBRB由于具有较普通BRB更大的极限变形能力,因而其受拉侧和受压侧的应变强化较普通BRB更加显著,且试件受压侧强度要高于受拉侧,这主要由材料的泊松效应和受压侧芯材与约束板件之间的接触引起.
3.2 变形与破坏模式
所有试件的破坏皆发生在受拉半圈,破坏皆由于芯材的延性断裂造成.试验结束后将PBRB拆卸并采用有机溶液除去无粘结材料,可以观察到试件的破坏模式.3个试件的破坏模式分别如图7~图9所示.从图中可以发现,3个试件在芯材通长不同的位置都产生了细小的裂缝,并且均由一条主裂缝的发展导致试件最终破坏.这表明芯材的材料延性得到了充分的发挥,从而使得PBRB具有优良的极限变形能力.单排孔试件的主裂缝出现在其中一个防滑块的边缘处,如图7所示.两排孔试件的主裂缝出现在芯材四分之一长度处的“短柱”中间位置,如图8所示.三排孔试件的主裂缝出现在芯材端部“短柱”顶端,如图9所示.如图6(a)所示,单排孔试件在拉伸变形段发生破坏,同时“短柱”长细比较小,主要发生平面外整体屈曲变形,没有观察到芯材明显的剪切变形,但可以发现“短柱”局部的平面内弯曲变形.如图6(b)(c)所示,两排孔试件拉断时变形仍处于压缩变形段,三排孔试件在接近原始未变形位置处发生破坏.两排孔和三排孔试件均可以观察到芯材明显的剪切变形,如图8、图9所示.同时,在两排和三排孔试件中都可以观察到芯材“短柱”的平面外屈曲变形,表明PBRB受压侧变形包含平面内、外弯曲和芯材整体的剪切变形,同时当“短柱”长细比较小时还可能发生“短柱”的平面内变形.3个试件都可以在芯材开孔处端部及“短柱”中部发现细小的裂纹.在连接处没有出现裂纹,证明本文所提PBRB构造细节的设计是合理的.
试验过程中,由于两侧盖板的存在,无法观察试件内部芯材的变形全过程.由于所有试件芯材均在受拉半圈被拉断,仅从芯材的破坏模式难以精确定量分析其受压变形,因此需要通过有限元对试验全过程进行模拟,以确定试件芯材的变形模式.
通过有限元软件ABAQUS 6.13建立3个试件的三维实体模型.在有限元分析中考虑了材料塑性及构件间的接触,采用缩减积分单元C3D8R以保证软件处理高度非线性问题的计算效率及精度.材料本构中真实应力-真实应变数据由图3的工程应力-工程应变曲线换算得出,滞回加载下的塑性模型选择Chaboche模型,模型参数通过材性试验结果拟合得出.有限元模型中芯材一端固接,另一端可移动并约束其平面外自由度.在芯材可移动端施加与试验相同的加载制度,如图5所示.通过在螺栓孔中心设置参考点并用参考点耦合螺栓孔表面自由度来模拟PBRB试件的螺栓.3个试件在+4%~-5%受压半圈芯材变形图如图10~图12所示.由图10可以发现单排孔试件的平面内剪切变形不明显,平面外受弯变形为主要变形模式,同时可以观察到“短柱”的平面内弯曲变形;由图11可以发现两排孔试件出现较为明显的平面内剪切变形,同时平面外弯曲变形明显,但是比单排孔的平面外变形小;由图12可以发现三排孔试件的平面内剪切变形和短柱局部弯曲变形明显,短柱发生了严重的平面内屈曲变形,同时平面外弯曲变形相对不明显.由图6(c)中所示的三排孔试件的平均应力-平均应变试验滞回曲线可以发现受拉破坏前受压侧的屈曲后性能稳定,没有出现明显的承载力下降.由有限元结果可以发现三排孔试件性能劣于两排孔和单排孔试件的原因在于其受压侧局部“短柱”过大的变形造成等效塑性应变过大,3个试件最大等效塑性应变分别为1.00、1.00和1.50,造成“短柱”处塑性损伤累积速度相对于其它2个试件快,从而导致了过早的延性断裂.结合试验与有限元分析结果,可以确定PBRB芯材“短柱”的屈曲后断裂性能是影响PBRB的整体耗能能力和累积延性性能的关键因素.
(a)芯材变形平面图
(b)芯材变形侧视图
(a)芯材变形平面图
(b)芯材变形侧视图
(a)芯材变形平面图
(b)芯材变形侧视图
3.3 初始刚度
由荷载-位移曲线第一圈弹性受拉段可求得3个试件的初始刚度,分别为167 kN/mm、142 kN/mm和116 kN/mm.可以发现,随着芯材开孔数增多,截面最小截面积减小,试件的初始刚度有所降低.由于芯材的截面在长度方向是变化的,不能简单地通过公式K=E0A/L来计算其初始刚度的理论值.本文将芯材分成多个基本单元分别计算刚度,根据几何关系,把各单元刚度进行合理的串并联,以求得芯材初始刚度的理论值.下面对初始刚度的计算方法进行简要介绍.
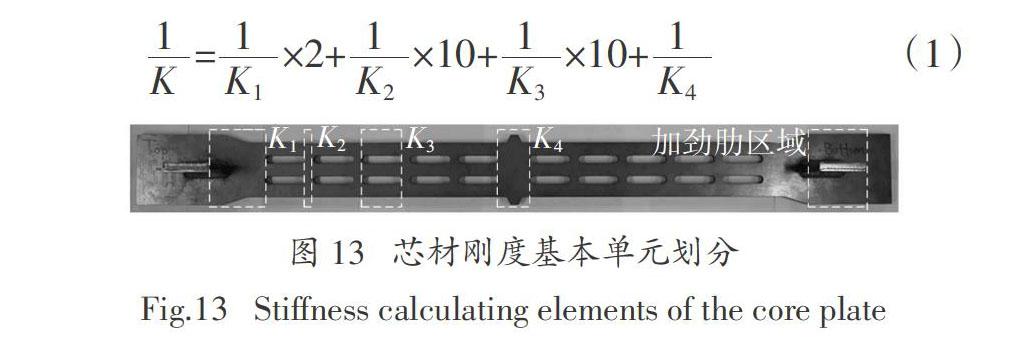
以两排孔试件为例,将芯材主要分为如下几个基本单元:芯材端部K1、孔间部分K2、开孔部分K3及防滑块部分K4,如图13所示.结合图1(b)的几何尺寸,可以确定两排孔试件的芯材共有2个K1单元、10个K2单元、10个K3单元及1个K4单元.对于每个基本单元,都可以通过公式Ki = E0Ai /Li计算出相应刚度,芯材可以视为由这些单元通过串联的方式组成,故芯材初始刚度K可以通过式(1)计算得出.
由相同的計算原理,可以计算出单排孔试件和三排孔构件的初始刚度.3个试件的理论计算刚度分别为184 kN/mm、160 kN/mm和134 kN/mm,理论值与试验值的比值分别为1.10、1.13和1.15.初始刚度的理论计算值与试验值相差不大,能够较好地预测试件的初始刚度.
3.4 耗能性能与延性
我国《建筑抗震试验方法规程》[10]通过定义耗能系数E来衡量试件的能量耗散能力.根据其定义,求得PBRB试件的耗能系数如表2所示.可以发现,3个试件均具有较大的耗能系数,分别为3.71、3.20和3.00,均大于3.00,体现了PBRB良好的耗能性能.随着芯材开孔数的增多,PBRB的总耗能及耗能系数均随之降低.
在抗震减震结构设计中,等效粘滞阻尼比ξeq是反映消能减震构件对结构减震耗能作用大小的一个重要参数,也是线性反应谱分析的关键参数.根据《建筑抗震试验方法规程》定义的计算方法,可由式(2)得出ξeq.其中E为耗能系数.计算结果如表2所示,3个试件的等效粘滞阻尼比分别为0.59、0.51和0.48.3个试件都有较大的等效粘滞阻尼比,接近0.5,说明PBRB具有良好的等效阻尼性能.此外,BRB的延性通常由两个参数进行评估:一个是累积延性系数μc,通过式(3)对应可得;另一个是最大延性系数μmax,通过式(4)可得.
式中:Δmax为BRB的最大变形;Δy为BRB的屈服变形;∑Δp为BRB的累积塑性变形.
以往研究表明,在美国,对于50年超越概率为2%地震作用下的屈曲约束支撑框架体系(BRBFs),最大延性系数μmax需要达到20~25[11].美国设计规范规定:对于BRBF,累积延性系数μc需要大于200[12].当BRB的延性系数低于需求值时,在强震作用下BRB就可能发生破坏.
由式(4)计算得出试件的最大延性系数μmax,如表2所示.3个试件的最大延性系数分别为33.7、34.6和20.1.可以发现,单排孔试件和两排孔试件的最大延性系数均超过了30,远大于μmax需达到20~25的要求;三排孔试件的最大延性系数为20.1,落在20~25的区间内,可以认为满足要求.对比单排孔和两排孔试件的μmax可发现,芯材的合理开孔可以提高BRB的最大延性.而三排孔试件的μmax相比前2个试件小得多,这是由于芯材不合理的开孔设计,导致开孔处“短柱”的长细比过大,弹塑性屈曲后滞回性能较差,降低了试件最大延性.
由式(3)计算得出试件的累积延性系数μc,如表2所示.3个试件的累积延性系数分别为425、399和152.可以发现单排孔试件的累积延性略大于两排孔试件,都具有较大的累积塑性变形,均能够满足BRBF的μc大于200的要求;三排孔试件的累积延性最小,小于200.此处,需要注意的是,本文采用的加载幅值较大,若在规范指定的加载制度下,三排孔试件的μc也能超过200的可能性较大.同时,在本文研究的参数范围内,随着芯材开孔处“短柱”长细比的增大,PBRB芯材的累积延性逐渐降低.
4 结 论
本文提出了一种芯材开有类椭圆孔的新型全钢制开孔屈曲约束支撑(PBRB).本文通过试验考察了不同开孔设计对PBRB试件的变形机制及破坏模式的影响.相对于普通BRB,本文提出的PBRB具有良好的极限变形能力.PBRB压缩变形不仅包含芯材的轴向压缩变形、高阶整体屈曲产生的弯曲变形,还有格构式开孔芯板的剪切变形等.
试验结果显示PBRB具有稳定的滞回性能、良好的延性和累积耗能能力.开孔芯材“短柱”的长细比是影响PBRB抗震性能的关键参数,长细比最大的试件(三排孔试件)的延性性能明显不及长细比相对较小的2个试件(单排孔和两排孔试件).
本文同时给出了PBRB的初始刚度估算方法,理论计算值与实际测量值接近,该方法可以通过几何尺寸较好地预测PBRB试件的初始刚度.此外,本研究设计的新型节点将加劲肋焊缝外移至芯材截面放大处,该构造很好地防止了节点的平面外失稳,同时也避免了焊缝的过早破坏.
此外,本文发现单排孔屈曲约束支撑虽然没有发生明显的剪切变形,但其累计延性性能最好,相关变形和破坏机理需要进一步阐明.
在实际工程应用中,基于目前试验研究结果,PBRB芯材开孔规则应与试验试件在原理上相一致.在保证盖板约束能力的前提下,根据实际结构承载力合理选择芯材尺寸,保守建议芯材开孔保证“短柱”长细比不大于10.4;可适当增大开孔面积以保证端部节点在支撑达到最大承载力时仍然保持弹性;同时,减少开孔数量,以有利于降低加工难度,有效控制误差,并减少加工费用,提升PBRB工程应用的经济性.
参考文献
[1] 汪家铭,中岛正爱,陆烨.屈曲约束支撑体系的应用与研究进展(Ⅰ)[J].建筑钢结构进展,2005,7(1):1—12.
UANG C M,NAKASHIMA M,LU Y. The practice and research development of buckling-restrained braced frames[J]. Progress in Steel Building Structures,2005,7(1):1—12.(In Chinese)
[2] YOSHINO T,KARINO Y. Experimental study on shear wall with braces:Part 2[C]//Summaries of Technical Papers of Annual Meeting. Tokyo:Architectural Institute of Japan,1971:403—404.
[3] 胡宝琳,李国强,孙飞飞.屈曲约束支撑体系的研究现状及其国内外应用[J].四川建筑科學研究,2007,33(4):9—13.
HU B L,LI G Q,SUN F F. The current research and application of home and abroad of buckling-restrained brace[J]. Sichuan Building Science,2007,33(4):9—13.(In Chinese)
[4] 陈云,吕西林,蒋欢军.新型耗能增强型形状记忆合金阻尼器减震性能研究[J].湖南大学学报(自然科学版),2013,40(2):31—38.
CHEN Y,L X L,JIANG H J. Seismic performance study on new enhanced energy dissipation SMA damper[J]. Journal of Hunan University (Natural Sciences),2013,40(2):31—38.(In Chinese)
[5] 胡晓斌,李文霞,刘坤,等.外置金属阻尼器的新型自复位约束砌体墙抗震性能研究[J].湖南大学学报(自然科学版),2016,43(7):50—56.
HU X B,LI W X,LIU K,et al. Seismic performance of a new type of self-centering combined masonry wall with external steel dampers[J].Journal of Hunan University(Natural Sciences),2016, 43(7):50—56.(In Chinese)
[6] JIA L J,GE H B,MARUYAMA R,et al. Development of a novel high-performance all-steel fish-bone shaped buckling-restrained brace[J]. Engineering Structures,2017,138:105—119.
[7] HAGINOYA M,TAGUCHI T,NAGAO T,et al. Experimental studies on mechanical properties for buckling-restrained braces with slit holes[J]. Steel Construction Engineering,2008,15(57):35—43.
[8] 周云,钱洪涛,褚洪民,等.新型防屈曲耗能支撑设计原理与性能研究[J].土木工程学报,2009,42(4):64—71.
ZHOU Y,QIAN H T,CHU H M,et al. A study on the design principle and performance of a new type of buckling-resistant brace[J]. China Civil Engineering Journal, 2009, 42(4): 64—71.(In Chinese)
[9] 邓雪松,纪宏恩,张文鑫,等.开孔板式屈曲约束支撑拟静力滞回性能试验研究[J]. 土木工程学报,2015,48(1):49—55.
DENG X S,JI H E,ZHANG W X,et al. Quasi-static cyclic tests on hysteretic behavior of a perforating plate buckling-restrained brace
[J]. China Civil Engineering Journal,2015,48(1):49—55.(In
Chinese)
[10] JGJ/T 101—2015 建筑抗震試验规程[S].北京:中国建筑工业出版社,2015:14—15.
JGJ/T 101—2015 Specification for seismic test of buildings[S]. Beijing:China Architecture & Building Press,2015:14—15.(In Chinese)
[11] FAHNESTOCK L A,SAUSE R,RICLES J M,et al. Ductility demands on buckling-restrained braced frames under earthquake loading[J]. Earthquake Engineering and Engineering Vibration,2003,2(2):255—268.
[12] ANSI/AISC 341-10 AISC Seismic provisions for structural steel buildings[S]. Chicago IL:American Institute for Steel Construction,2010:249—258.
