基于遗传算法优化双管掺水集油工艺参数

才浩楠 王世海 黄文才 王子墨 柴彦强 杨永

1华北油田公司工程技术研究院

2华北油田公司第一采油厂

3华北油田公司第五采油厂

4华北油田华港燃气集团有限公司

5华北油田公司二连分公司

6渤海钻探工程有限公司国际钻采物资供应分公司

华北油田二连区块某采油区采用双管掺水集油工艺，热水由联合站到计量站（计配站），再到各个单井，与产出液混合后返回。

该工艺热力和动力损耗主要通过调节掺水温度、各个单井掺水流量进行控制，而掺水温度和掺水流量与地面温度、管道参数、产出液的物性等因素有关。现场人员在调节掺水温度和掺水流量的过程中，由于缺少对相关影响因素的定量了解，采用模糊调节或人工经验调节，导致回液温度往往高于回液凝点10～15℃，远远超出经济运行成本。为了降低能耗，需要了解掺水参数与回液温度的量化关系。

1 数学模型的建立

1.1 目标函数

1.1.1 管道沿程热力损耗

直线传输管道的散热量采用传统舒霍夫温降公式[1]计算，但传统舒霍夫温降公式并未考虑管道水力摩擦所损失的热量。所以应采用修正后的舒霍夫公式[2]，即在考虑摩阻热的前提下，假设某输油管道的外径为D，输量为G，周围介质的温度为T0，取dL微元段上的油温为T，水力坡降取为i，原油在dL上产生的温降为dT。在稳定工况下，dL段上的热平衡方程为

式中：K为管道总传热系数，W/（m2·℃）；D为管道外直径，m；i为水力坡降；G为油品的质量流量，kg/s；C为平均温度下油品的比热容，J/(kg·℃)； g为重力加速度，m/s2；T0为环境温度，℃。

式（1）左边部分为管线向周围介质的散热量，右边为油流温降放热和摩阻热之和。随着dL增大，dT变小，因而引入负号。将式（1）进行变形后，即可得到考虑摩擦生热的舒霍夫温降公式，即修正后的舒霍夫温降公式[3]为

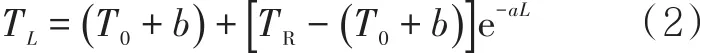
式中：a=KDπ/GC，b=gi/Ca； L为管道长度，m；TR为管道起点油温，℃；TL为距起点L处油温，℃。

但在实际生产过程中，由于复杂的现场工况，使得用上述公式计算出来的传热系数K[4]和实际传热系数相比误差较大。为了减少这种误差，通常采用反算法[5]计算管道传热系数K，公式为

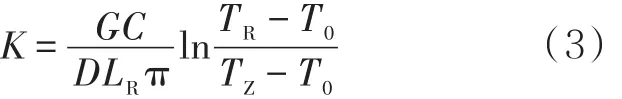
1.1.2 产出液混合热力变化

在单井产出液混合过程中，若不考虑碰撞所损失的热量[6]，各集油管线起点的温度应该为上一段管线内介质与油井产液混合后的温度[7]，经整理后得出

式中：Tj为产出液的温度，℃；CW为水的比热容，J/(kg·℃)；GW为掺水量，kg/s；TW为水的温度，℃；Ci为产出液比热容，J/(kg·℃)；Gi为产出液流量，kg/s；Ti为产出液温度，℃；Cj为混合后液体的比热容，J/(kg·℃)；Gj为混合后液体的流量，kg/s。

现场只能人工调节掺水温度和每口单井的掺水流量[8]，所以将掺水温度定位为变量 x，各单井掺水量定义为变量 y1,y2,…,yn，管道参数、环境温度、产出液物性等参数设定为常量，考虑热力消耗为集输系统运行的主要费用，建立目标函数f(x ,y,y,…,y)[9]。12n

式中：n为第n口井；m为井数；ΔQ1为从联合站到单井流体的比热容，J/(kg·℃)；ΔQ2为单井到联合站流体的比热容，J/(kg·℃)；Cow为从单井到联合站流体的比热容，J/(kg·℃)；TLw为流体在单井处的温度，℃；TLo为混合液返回联合站的温度，℃。

1.2 约束条件

1.2.1 压力约束

采用Beggs-Brill两相流压降模型[10]

式中： ρ1为液相密度，kg/m3； H1为截面持液率；ρg为气相密度，kg/m3；νsg为气相折算流速，m/s；θ为管路倾角；νm为气液混合物流速，m/s；Gm为气液混合物质量流量，kg/s；λm为摩阻系数。

由于混合液体返回联合站时，考虑联合站进口处的装备，压力不易过高，但若使流体能够顺利进入三相分离器，压力又不易过低，所以进站压力应保持在0.2～1.5 MPa[11]。为了保证井口顺利出液，井口回压 p应小于1.5 MPa。

1.2.2 温度约束

为了保证产出液能顺利集输到联合站，并在中途管道不发生析蜡、冻堵等现象，回液温度应大于原油凝固点 3～5 ℃[12]。

综上所述，双管掺水优化问题转化为非线性约束多变量的优化问题，其数学模型可以表示为

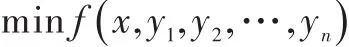
s.t.0.2 MPa＜p进站＜1.5 MPa；p回压＜1.5 MPa；

T回液＞凝固点+5℃

2 遗传算法求解模型

遗传算法[13]是计算数学中用于解决最优化的搜索算法，是进化算法的一种。遗传算法通常实现方式为一种计算机模拟。对于一个最优化问题，一定数量的候选解（称为个体）的抽象表示（称为染色体）的种群向更好的解进化。在每一代中，评价整个种群的适应度，从当前种群中随机地选择多个个体（基于它们的适应度），通过自然选择和突变产生新的生命种群，该种群在算法的下一次迭代中成为当前种群。

2.1 初始化种群

确定个体的个数、适应度、迭代次数等参数,并自定义函数Initialize用于初始化染色体，对染色体进行随机赋值并利用chrom_range将其限定在变量规定的区间之内。Matlab实现代码如下：

function chrom_new =Initialize(N， N_chrom，chrom_range)

chrom_new=rand(N，N_chrom);

for I=1:N_chrom

chrom_new(:，i)=chrom_new(:，i)

end

2.2 计算适应度函数

适应度函数[14]用于评判每一条染色体的适应度，并保留适应度高的染色体，淘汰适应度差的染色体。确定一个适应度矩阵，记录当前N条染色体的适应度，Matlab实现代码如下：

Function fitness=CalFitness(chrom，N，N_chrom)

Fitness=zeros(N，1)

For I=1:N

x=chrom(i，1);

y=chrom(i，2);

fitness(i)=min f（x,y1,y2…yn）

2.3 迭代流程

染色体变异、交叉，并计算适应度[15]，寻找最优染色体，替换当前存储的最优染色体，优胜劣汰。迭代流程如图1所示。

图1 迭代流程图Fig.1 Iterative flow chart

3 实例求解

选取某采油区5口油井，1个计量站，1个联合站，采用双管掺水集输工艺，通过建立非线性约束多变量的优化模型，采用遗传算法进行优化，计算出最优掺水温度与每口单井的掺水量。

以该地区2018年7月份的数据为例进行优化（取杂交率0.2，变异率0.2，种群大小500，遗传代数200），优化前后的掺水量和掺水温度如表1所示。由图2可以看出，每口井掺水量在优化后平均下降了大约40%～50%，掺水温度优化前后相差4℃，热力日损耗降低了20%～25%。

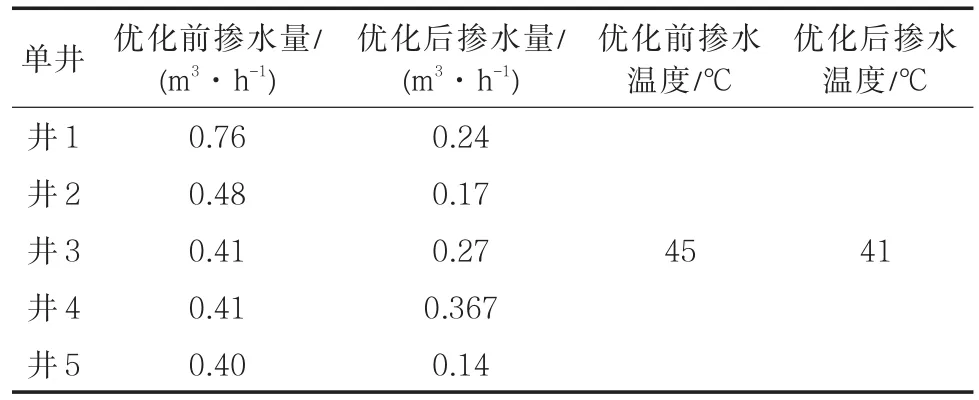
表1 优化前后掺水量与掺水温度比较Tab.1 Comparison of water-blending amount and temperature before and after optimization

图2 优化前后消耗热能比较Fig.2 Comparison of heat loss before and after optimization

4 结束语

通过建立修正舒霍夫管道温降模型，得出比较贴切现场实际的管道温降模型，确定了掺水参数与回液温度的定量关系，以回液温度、进站压力、井口压力作为边界条件，将实际问题转化为多变量非线性约束的优化问题，通过遗传算法进行优化，得出最优掺水温度和掺水流量，降低了某工区的日能耗。