卫星微振动液阻隔振器建模与试验研究

刘巧斌， 史文库， 柯俊， 陈志勇,*， 曹飞， 闵海涛

(1. 吉林大学 汽车仿真与控制国家重点实验室, 长春 130022; 2. 浙江理工大学 机械与自动控制学院, 杭州 310018)

卫星上所搭载的精密仪器设备经常处于低频微幅的振动环境中。液体阻尼式隔振器(简称液阻隔振器)是一种广泛应用于卫星微振动隔离的隔振装置[1-5]。

建立准确、简洁而物理意义清晰的隔振器模型，是进一步对隔振器进行性能预测、结构改进以及优化控制的基础。国内外学者在液阻隔振器建模方面进行了大量的研究，建立了各式各样的液阻隔振器模型，总体而言可以分为3类：第1类为质量-弹簧-阻尼元件模型，通过将隔振器等效为一些简单的质量、弹簧和阻尼元件的串并联，从而实现隔振器性能的仿真预测[6-8]；第2类为流体力学集中质量模型，通过建立流体力学模型，根据力学等效原理，将连续流体等效为集中质量，对液体阻尼的非线性特性进行分析[9-10]；第3类为流固耦合有限元模型，这种建模方法通过建立隔振器的流体-固体耦合作用的有限元分析模型，并在有限元模型中施加载荷激励与提取响应，从而计算隔振器的动特性[11-12]。

分数阶导数建模方法是介于第1类和第2类的新方法，这种建模方法来源于黏弹性材料的分数阶本构模型。近年来，学者们引入分数阶导数建立了隔振系统模型，取得了一系列成果[13-16]。分数阶导数模型能够在使用较少的参数条件下，实现对黏弹性材料宏观力学性能的准确预测[17-19]，因此本文采用一种改进型分数阶导数模型对波纹管式液阻隔振器进行建模，并通过试验验证模型的正确性。

1 隔振器结构和工作原理

本文所研究的隔振器是一种波纹管式液阻隔振器，主要用于卫星微振动的隔离。图1为波纹管式液阻隔振器的结构示意图。隔振器的主要承载功能由外部的金属波纹管承担，并通过金属波纹管的弹性变形吸收振动能量，从而实现振动的隔离。此外，阻尼板上下的波纹管构成的液室在外部载荷的作用下，产生体积膨胀效应和活塞泵吸效应，这2个效应使得上下液室存在压力差，在压力差的作用下，液体通过阻尼通道来回振荡运动，产生阻尼，消耗振动能量，实现冲击振动的快速衰减。

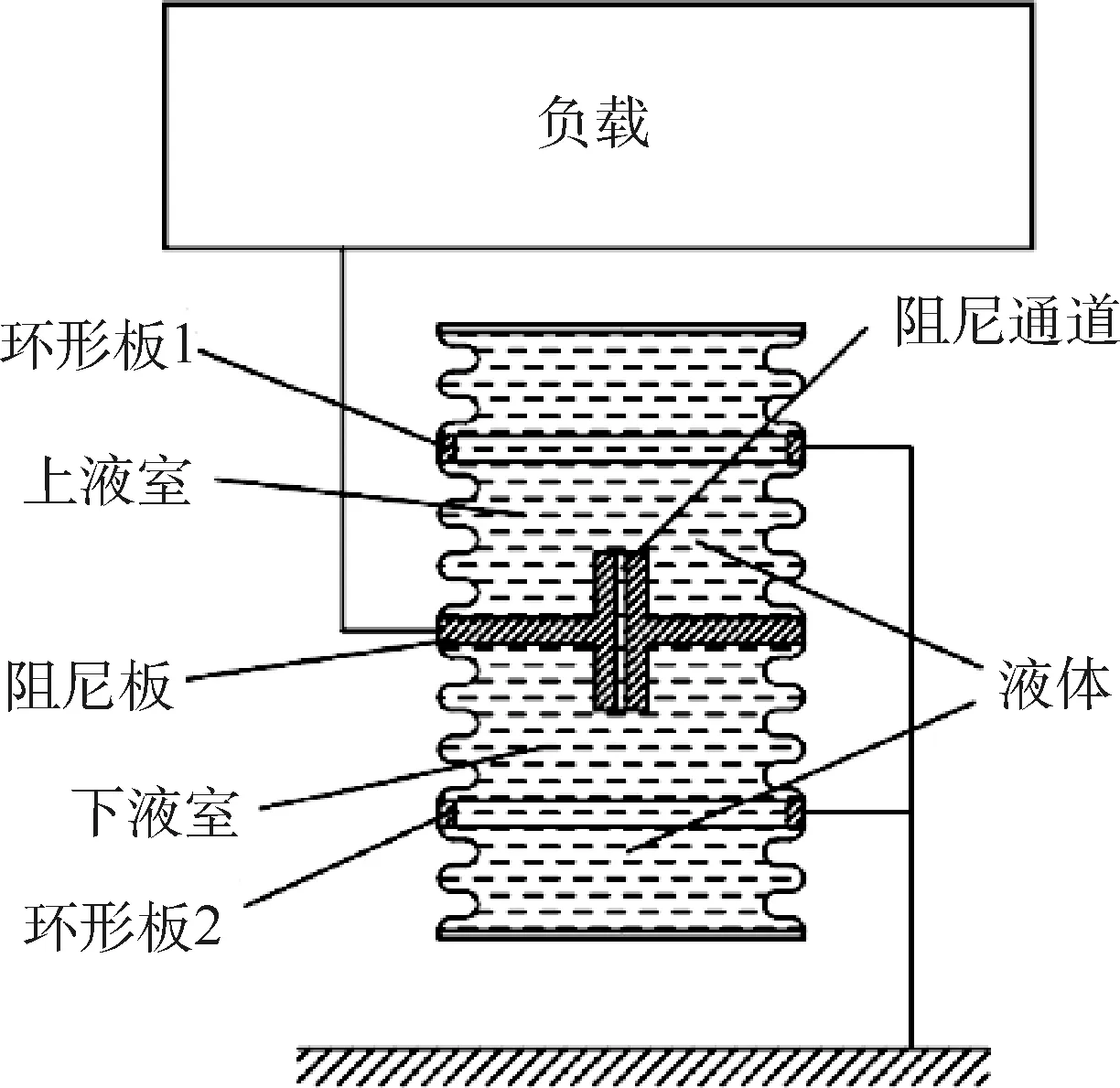
图1 波纹管式液阻隔振器结构示意图Fig.1 Schematic diagram of bellow type vibration isolator with hydraulic damping

在静态载荷和动态载荷的作用下，波纹管式液阻隔振器呈现出不同的刚度和阻尼特性，其刚度阻尼特性具有明显的随激励频率变化的频变特性和随激励振幅变化的幅变动特性。

2 改进型分数阶导数模型

为了实现对波纹管式液阻隔振器频变、幅变动特性的模拟，借鉴Pritz[16]所提出的五参数黏弹性材料本构关系模型，建立波纹管式液体阻尼隔振器的五参数分数阶导数模型，在此基础上，进行参数的幅值相关性修正，从而建立起可以同时进行频变和幅变分析的改进型分数阶导数模型。黏弹性材料的分数阶导数本构关系模型为

(1)

式中：σ(t)为应力；ε(t)为应变；K0、K∞、τ、α和β分别为分数阶导数本构关系模型的5个参数，可由时间的应力应变关系曲线的拟合获得。

对式(1)进行拉普拉斯变换，获得材料的微观弹性模量表达式，将其推广至宏观上，可得复刚度表达式，即

(2)

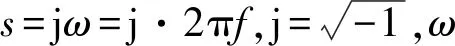
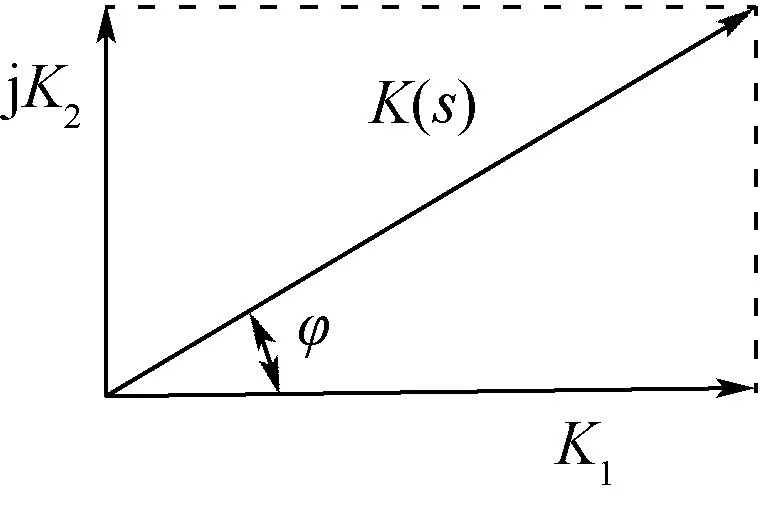
图2 复刚度、存储刚度和损耗刚度三者之间的几何关系Fig.2 Geometric relationship among complex stiffness, storage stiffness and loss stiffness

由式(2)的复刚度，进一度定义动刚度和滞后角的表达式分别为

(3)

(4)

式中：动刚度Kd的数值大小即为图2中的对角线长度。

结合波纹管式液体阻尼隔振器的结构和实测动特性曲线，对式(2)的分数阶导数模型进行改进，考虑幅变特性对5个参数的影响，将分数阶导数模型改进为

k(s,x)=ks(x)+(k1(x)-

(5)

式中：引入幅变因子x，将式(2)中的初始动刚度K0，高频动刚度K∞，时滞因子τ，分数阶因子α和β这5个参数由不考虑幅变特性的常数改进为含幅变特性的ks(x)、k1(x)、τ(x)、α(x)和β(x)这5个幅变参数。

3 幅变动特性模型参数识别

为了进行分数阶导数模型的参数识别，对波纹管式液阻隔振器进行动静特性试验。试验在MTS 831.10弹性试验机上进行。该试验台采用液压伺服控制系统产生作动位移，位移激励的最大振幅范围为±50 mm，最大激振力为25 kN, 最大激振频率为200 Hz。图3(a)所示是试验台的示意图，通过上下夹具将隔振器固定在试验台上，在夹具上下端分别布置有力传感器，在下夹具下方设置有作动器，作动器通过液压伺服系统产生所需的位移激励。图3(b)所示是动静特性试验台的实物图。通过在隔振器下端施加位移振动激励载荷，在隔振器上方测量传递力，从而计算获得实际的刚度和阻尼。在静特性试验时，分别采集位移激励幅值最大值为0.1、0.5、1.0、1.5和2.0 mm的5组数据，获得隔振器的位移-力滞回特性曲线，通过计算滞回曲线的斜率，即可得到隔振器的静刚度。在动特性试验时，分别施加位移振幅为0.1、0.2、0.4、0.6、0.8和1.0 mm，频率为5～200 Hz的正弦扫频位移激励6组。由于试验台激振器作动频率的限制，扫频激励最小频率为5 Hz，扫频频率间隔为1 Hz。

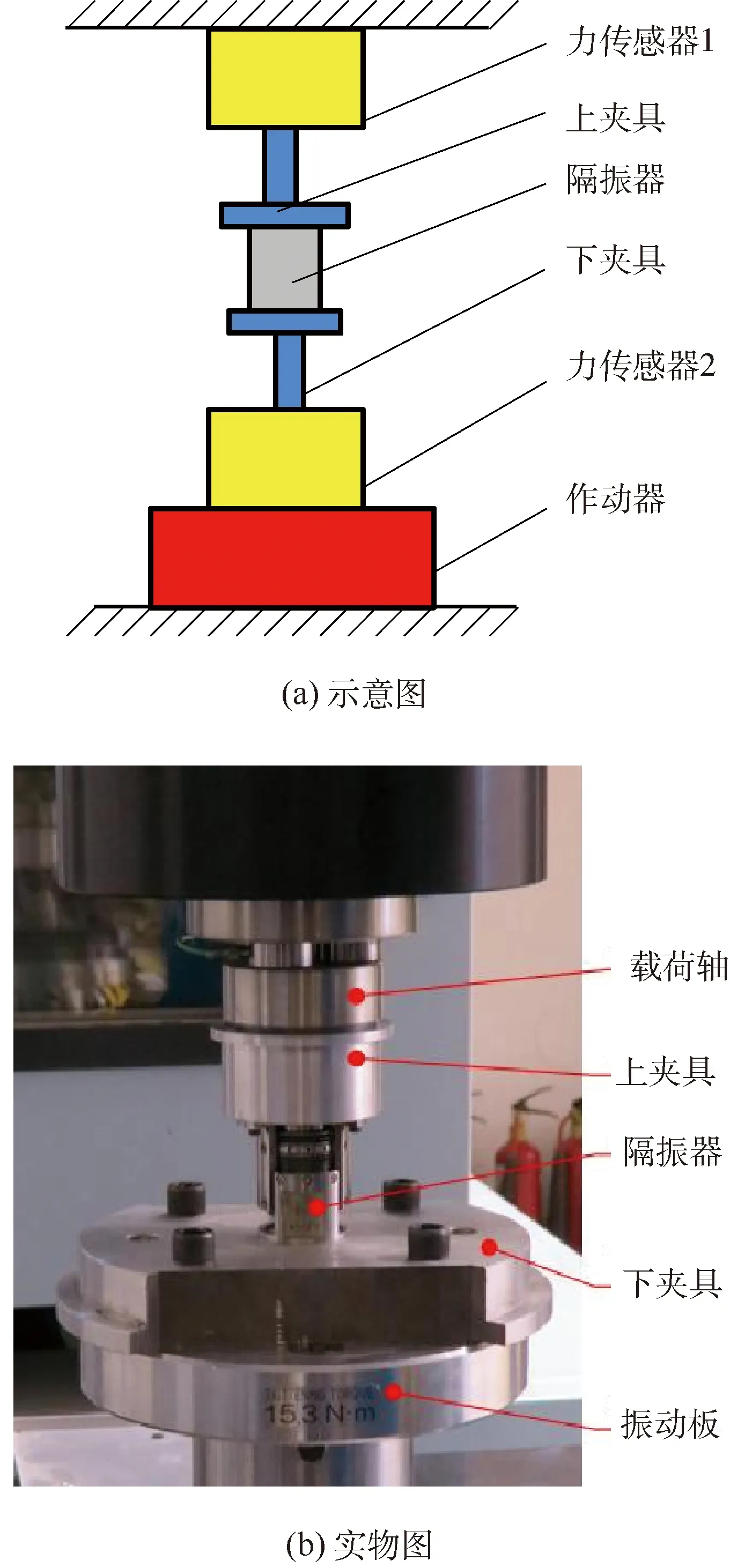
图3 隔振器动静特性试验台示意图和实物图Fig.3 Schematic diagram and picture of dynamic and static characteristic testbed for vibration isolator

通过对比不同幅值的静刚度滞回曲线，发现位移激励对静刚度的影响很小。为了研究的方便，忽略金属波纹管静刚度的幅变特性，在分数阶导数模型中，令静刚度ks为常数。图4所示是位移激励最大幅值为1 mm时的隔振器静刚度特性曲线，根据试验曲线拟合获得静刚度ks=18.12 N/mm。图5所示是动特性扫频试验测得的隔振器被动端相对主动端的力传递率曲线，由图可知，随着位移激励振幅的增加，隔振器的隔振性能下降，说明所研究的隔振器适用于微振动的隔离，对于大幅振动的隔离性能不如微幅振动。

根据试验数据和式(3)～式(5)，通过调用MATLAB的nlinfit函数，采用非线性最小二乘法分别对试验幅变动特性曲线的参数进行识别。图6所示是模型参数识别的流程图。识别获得的不同幅值激励下的分数阶导数模型参数如表1所示。

分析表1的参数识别结果可知，4个参数呈现明显的幅值相关性。通过曲线拟合发现，使用二次多项式可以对这4个参数的幅值相关性进行有效的拟合，拟合结果如表2所示。由相关系数可知，拟合值和最小二乘法参数识别结果的相关系数达到0.96以上，说明拟合效果很好。4个参数的幅值相关性的二次多项式拟合结果表达式分别为

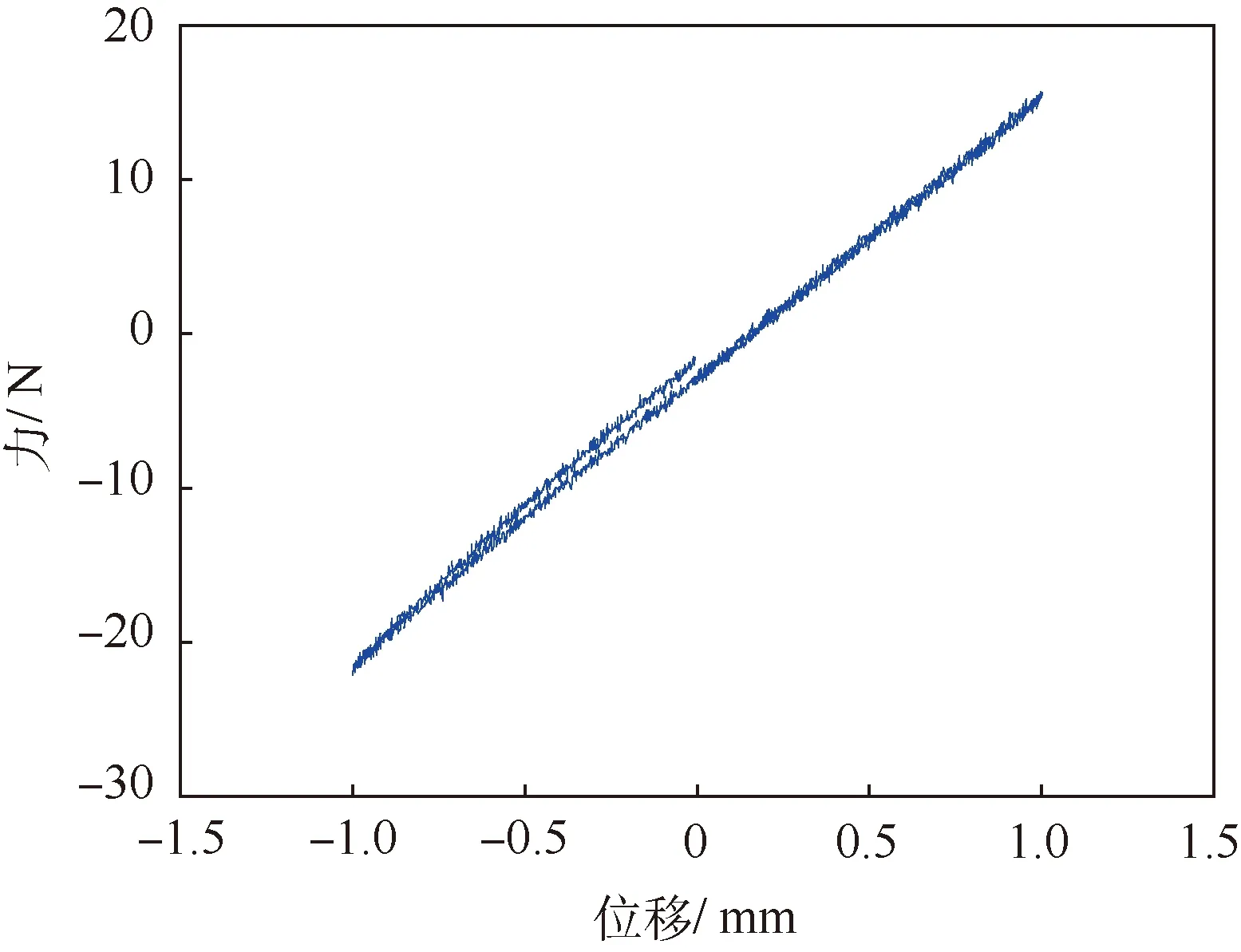
图4 隔振器静特性曲线Fig.4 Static characteristic curve of vibration isolator

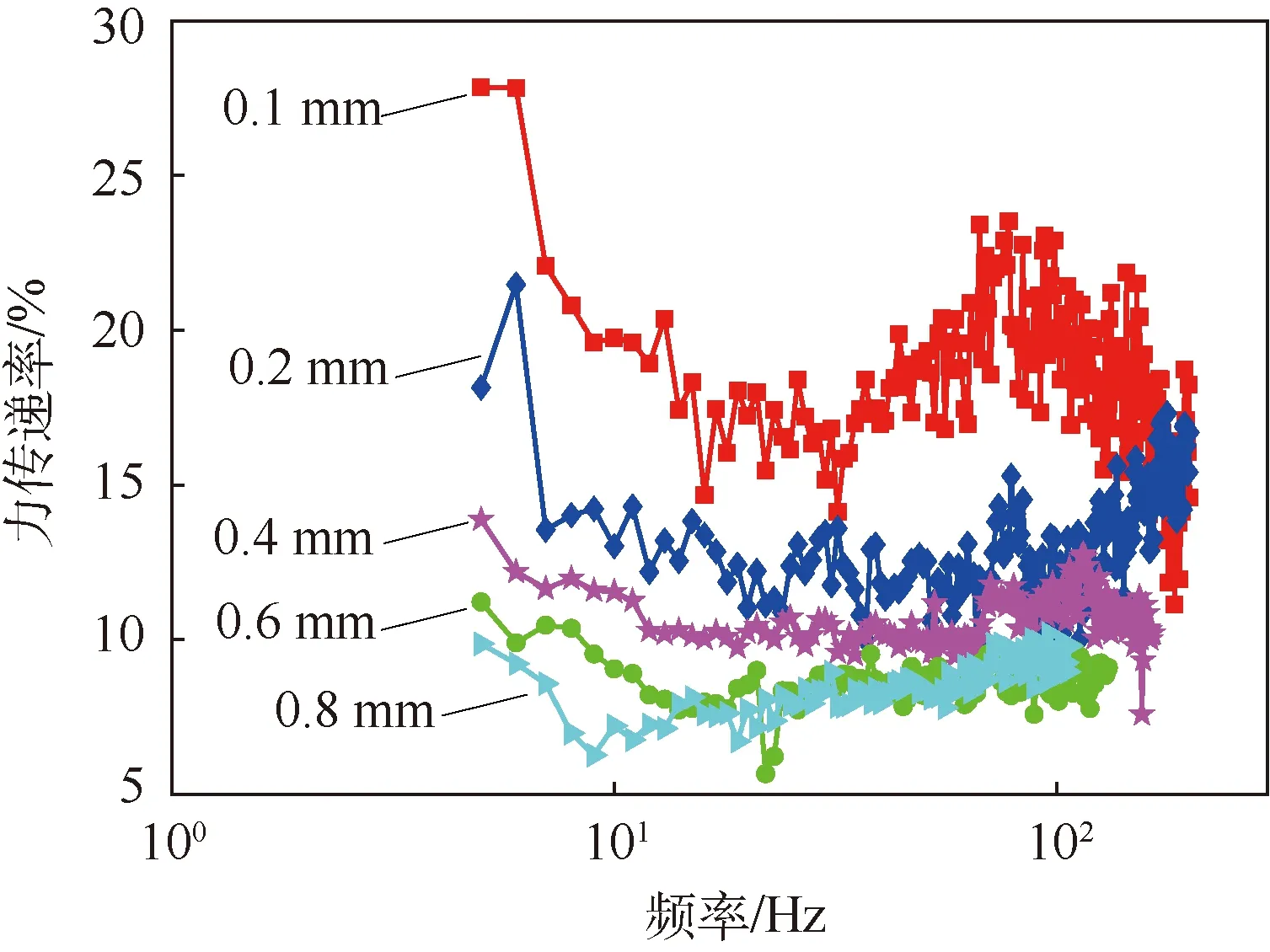
图5 隔振器动特性试验力传递率曲线Fig.5 Force transmissibility curves of vibration isolator in dynamic characteristic test

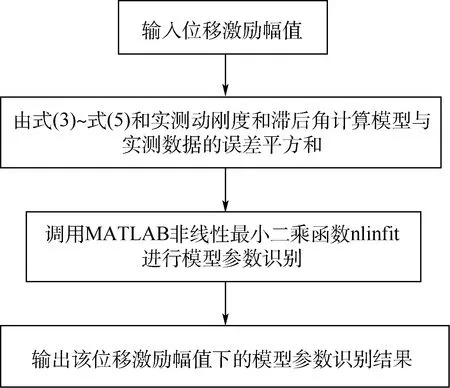
图6 模型参数识别流程图Fig.6 Flowchart of model parameter identification

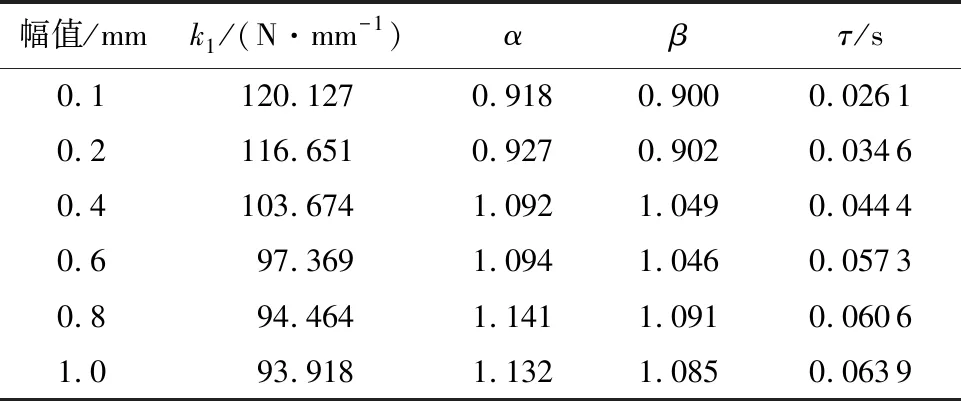
幅值/mmk1/(N·mm-1)αβτ/s0.1120.1270.9180.9000.02610.2116.6510.9270.9020.03460.4103.6741.0921.0490.04440.697.3691.0941.0460.05730.894.4641.1411.0910.06061.093.9181.1321.0850.0639

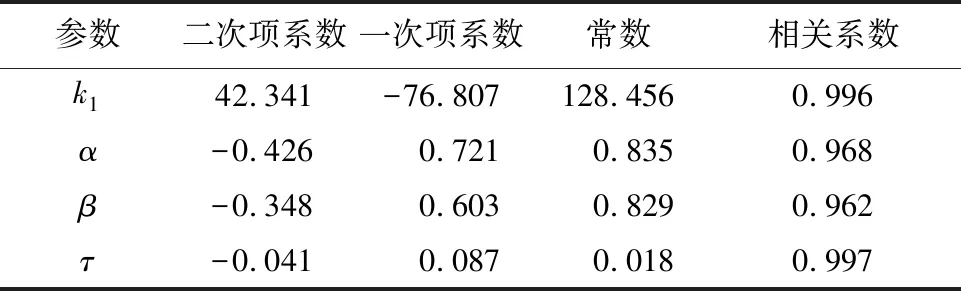
表2 参数识别结果的二次多项式拟合

k1(x)=42.341x2-76.807x+128.456

(6)

α(x)=-0.426x2+0.721x+0.835

(7)

β(x)=-0.348x2+0.603x+0.829

(8)

τ(x)=-0.041x2+0.087x+0.018

(9)

图7(a)～(d)所示分别是参数k1、α、β和τ的识别结果和拟合结果的对比。由图可知，动态硬化刚度k1随着激励幅值的增大而减小，说明位移激励的幅值越大，液体的高频动态硬化现象越小；而参数α、β和τ随着激励幅值的增加而增大，说明激励幅值增大，分数阶导数的阶次增加，液体阻尼增大，时滞增加，阻尼通道内的液柱共振频率减小。以上结论和相关液阻减振器的幅变动特性研究结论相一致[20-21]，并与试验结果相吻合，说明了理论建模和参数识别结果的可靠性。

联合式(5)～式(9)，用提出的改进型分数阶导数模型对隔振器的动特性进行仿真，并与实测数据进行对比，图8是在幅值为0.2、0.6和1.0 mm时采用改进型分数阶导数模型的仿真结果与实测动刚度和滞后角的对比。由仿真结果与实测结果的对比可知，采用改进型分数阶导数模型可以对波纹管式液阻隔振器的幅变、频变动特性进行准确的描述。实测动刚度曲线由于夹具和激振器的条件限制，存在一些噪声干扰，因此在数值上出现一些波动。

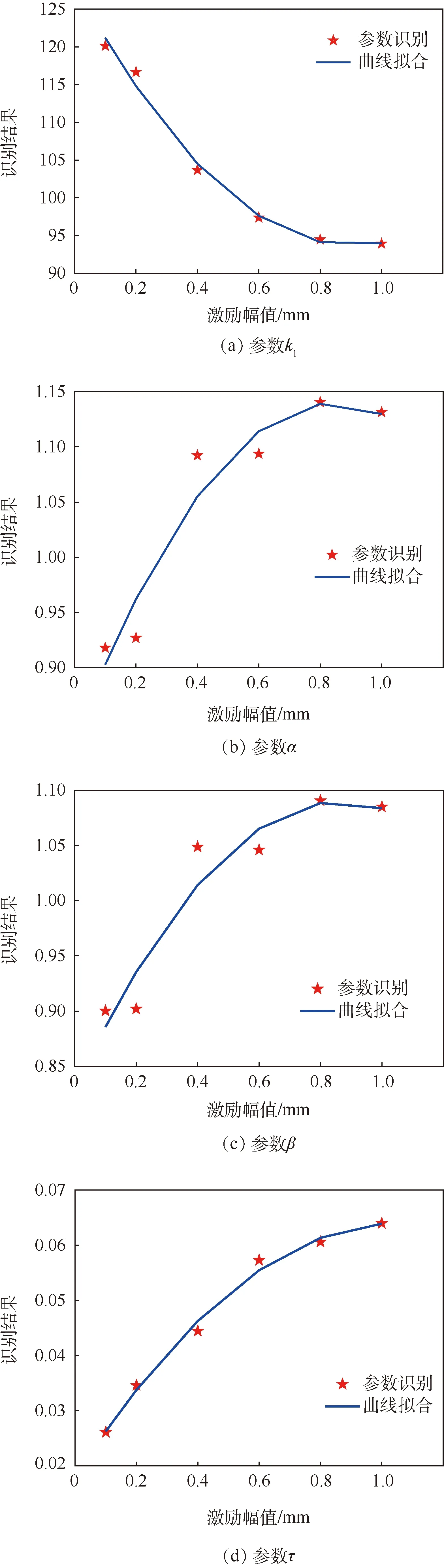
图7 参数k1、α、β和τ识别结果与拟合结果对比Fig.7 Comparison between identified and fitting results of parameter k1,α,β and τ

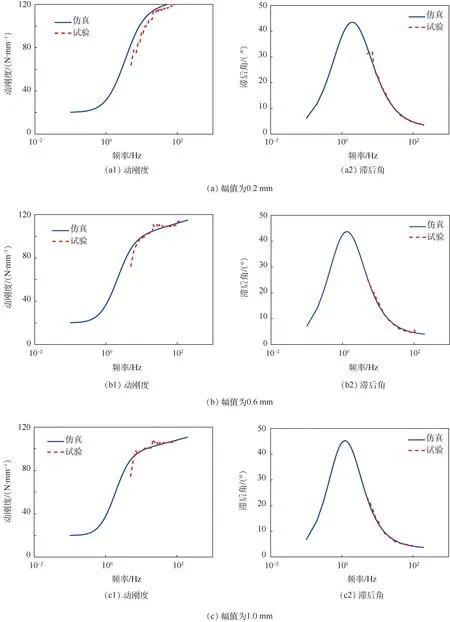
图8 不同幅值的动刚度和滞后角仿真与试验曲线对比Fig.8 Comparison of simulation and experimental dynamic stiffness and loss angle curves with different amplitudes

4 参数影响分析

为分析分数阶导数模型的主要模型参数对隔振器动特性曲线的影响。采用控制变量方法分别研究模型中5个参数分别相对初始参数变化0.8～1.2倍时相应的动特性曲线的变化情况。

图9所示是高频动刚度k1对动刚度和滞后角的影响,k10为初始值，由图可知，随着k1的增加，动刚度和滞后角增加，此外，k1主要影响高频动刚度和峰值滞后角的数值。

图10所示是静刚度ks对动刚度和滞后角的影响，ks0为初始值，由图可知，ks主要影响动刚度曲线的低频段和滞后角曲线的峰值，随着ks的增加，低频动刚度增大，滞后角峰值减小。

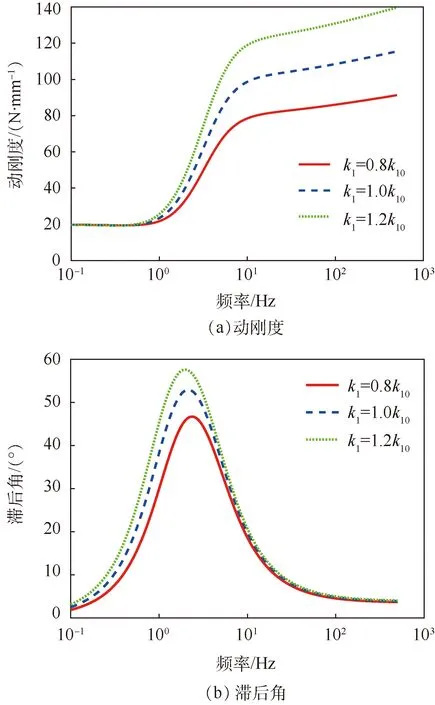
图9 参数k1对动刚度和滞后角的影响Fig.9 Influence of parameter k1 on dynamic stiffness and loss angle

图10 参数ks对动刚度和滞后角的影响Fig.10 Influence of parameter ks on dynamic stiffness and loss angle

图11所示是分数阶导数的分子阶次α和分母阶次β对动刚度和滞后角的影响，α0和β0为初始值。由图可知，这2个参数控制了隔振器动特性曲线的液柱共振区，分数阶因子α和β的数值越大，液柱共振区间范围的动刚度和滞后角越大，动刚度曲线的斜率越大，滞后角峰值越高，说明液体阻尼的惯性效应越明显。当分数阶次因子为1时，分数阶模型转化为线性速度阻尼系统，系统阻力主要与位移的导数成正比；而分数阶次因子为2时，系统转化为质量惯性系统，系统阻力主要与位移的二阶导数成正比。对于本文所研究的黏弹性液阻隔振器，分数阶因子介于1和2之间，在激励幅值小时，由于弹性力的影响更明显，分数阶因子出现略小于1的现象，与表1所示的参数识别结果所揭示的规律相一致。

图12所示是时滞因子τ对动刚度曲线和滞后角的影响，τ0为初始值。由图可知，τ改变后，曲线沿横坐标平移，说明时滞因子τ主要表征阻尼通道中液柱的共振频率，随着时滞的增加，共振频率减小，曲线整体左移。

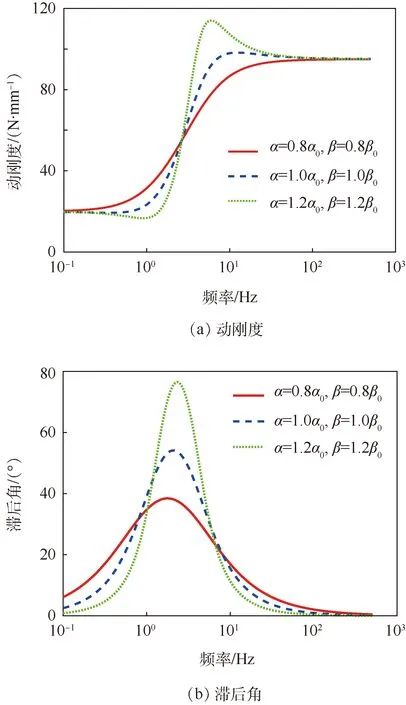
图11 参数α和β对动刚度和滞后角的影响Fig.11 Influence of parameter α and β on dynamic stiffness and loss angle

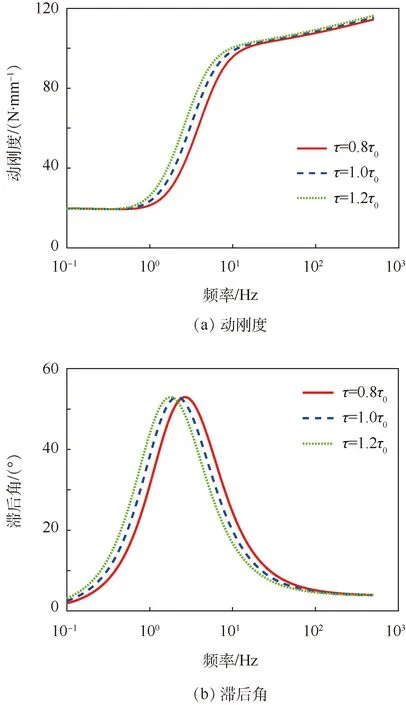
图12 参数τ对动刚度和滞后角的影响Fig.12 Influence of parameter τ on dynamic stiffness and loss angle

5 结 论

本文在分析了某卫星微振动液阻隔振器结构和工作原理的基础上，建立了隔振器改进型分数阶导数模型，对隔振器的幅变、频变动特性进行仿真，并与实测动特性曲线进行对比，验证了所提出的模型的正确性，可为类似微振动隔振器的动特性建模提供参考。主要结论如下：

1) 微振动液阻隔振器具有频变特性，在液柱共振时，隔振器动刚度和阻尼角出现峰值，从而可以提高隔振器衰减大幅振动的能力。

2) 微振动液阻隔振器具有明显的幅变特性，随着激励振幅的增加，分数阶的阶次因子逐渐增大，时滞因子逐渐增大，动态硬化等效线刚度逐渐减小，可采用二次多项式对分数阶导数动特性模型的参数幅变相关性进行拟合。

3) 由分数阶导数模型的参数影响分析结果可知，液阻隔振器的静刚度ks主要影响动刚度曲线的起点和滞后角曲线的峰值；动态硬化等效线刚度k1主要影响动刚度曲线的高频段和滞后角曲线的峰值；分数阶因子α和β共同决定了动刚度特性曲线共振区斜率和峰值频率；时滞因子τ主要影响动特性曲线液柱共振峰值频率点的位置。