端部带质量和弹簧约束悬臂梁振动响应的解析解
2019-05-29马斌捷周书涛贾亮侯传涛荣克林
马斌捷, 周书涛, 贾亮, 侯传涛, 荣克林
(北京强度环境研究所, 北京 100076)
运载火箭在垂直转运过程和发射前会受到地面风产生的静态和动态载荷作用,增加防风减载结构后,火箭根部的弯矩载荷可以大大降低。此时,火箭的受力状态与受到横向分布载荷作用悬臂梁的振动响应类似,可以利用等截面悬臂梁的振动响应解析研究结果来指导火箭的受力分析和结构设计。连续体振动响应的解析解是否能得到,主要取决于其运动方程和边界条件的复杂性。对于杆、轴、弦、膜等具有二阶导数运动方程的振动系统,其振型均为三角函数的线性组合,对应的广义质量和广义力可以通过解析积分获得,存在完备的振动响应解析解[1]。对于梁、板等具有四阶导数运动方程的振动系统,有显式或隐式特征方程,能得到特征根,但其振型为三角函数和双曲函数的线性组合,在全简支边界条件下振型退化为三角函数的线性组合时,存在振动响应的解析解,在其他边界条件下的振动响应解析解尚未见报道[1]。对于具有双四阶或八阶导数运动方程的壳体振动问题,存在众多对应不同假设的振动理论,其特征值的解比较繁杂,不便于工程使用与分析,并且其振动响应的解析解不存在[2-4]。
悬臂梁的动力学响应与附加质量大小、位置、转动惯量和支撑刚度等诸多因素密切相关,国内外的众多学者对此开展了大量的研究,但仅限于研究各种因素对悬臂梁振型和频率的影响,很少进一步研究这些因素对悬臂梁振动响应的影响。在考虑附加质量大小和位置的影响方面,尹传家和黄怀德[5]、刘树林等[6]给出了端部带质量约束悬臂梁的特征值解;Wang等[7]根据达朗贝尔原理将悬臂梁端部的集中质量等效为惯性力和惯性力矩,数值和实验研究了不同位置参数下梁的频率和位移响应;陆海桃和仝艳文[8]采用试验测量和有限元仿真相结合的方法,研究了集中质量的大小和位置对悬臂梁固有频率的影响规律;陈娟娟和刘杰[9]建立了带悬挂小球和摆杆竖直悬臂梁的动力学模型,分析了小球和摆杆质量对结构一阶模态的影响;杨一柳等[10]推导了双桥臂硅微悬臂梁谐振频率的解析式,研究了质量块长度对微悬臂梁谐振频率的影响;赵存生等[11]根据附加质量块的移动改变悬臂梁频率的原理,研制了悬臂梁动力吸振器。在考虑转动惯量的影响方面,Swaminadham和Michael[12]推导了考虑端部集中质量平动(剪切)和转动惯量的悬臂梁的频率方程,获得了不同质量比和转动惯量比时梁的前五阶频率值;王栋[13]建立了考虑集中质量平动和转动惯性的悬臂梁的频率特征方程,数值分析了集中质量的转动惯性对梁的频率、振型以及灵敏度的影响;Lajimi和Heppler[14]建立了考虑端部集中质量转动惯量的欧拉梁的特征方程,并计算了不同参数下梁的频率。在考虑支撑刚度的影响方面,杨帅和王太勇[15]建立了悬臂梁在竖直方向为弹性约束时的特征方程,并数值研究了梁的前三阶固有频率随约束刚度变化的规律。另外,蔡国平和洪嘉振[16]考虑梁横向变形引起的轴向变形的二次耦合量,研究了附加质量对中心刚体-悬臂梁系统动力学特性的影响;闫安志等[17]实验研究了动质量对悬臂梁共振响应的抑制效果;夏季等[18]获得了带多个集中质量和弹性支承等截面均质梁的振型函数,并建立了带集中质量简支梁和悬臂梁、跨中带弹性支承简支梁的特征方程;闫安志[19]和郭金泉[20]等考虑了裂纹深度和裂纹位置对悬臂梁系统固有频率的影响。
等直梁振动响应分析除两端均为简支边界时有解析解外,仅对于一端为固支、另一端分别为简支、固支和自由的3种等直梁有半解析解,对此Timoshenko等[1]依据Young和Felgar[21]给出的各种边界条件下的振型数值表,给出了集中力作用下的振动响应解。该振型表是通过数值方法将广义质量归一化,给出振型和各阶导数分布的数值结果。对于除两端简支以外其他边界条件的等直梁,其振型函数为含有双曲函数和三角函数的四项多项式。Timoshenko等[1]认为计算其分布力的广义力存在数学上的困难,因而未给出相应的解析解。但在数学手册中双曲函数与线性函数的乘积以及三角函数与幂函数的乘积均有解析积分式,因而可以得到均布力和线性分布力的广义力的解析积分结果[22-23]。广义质量与广义刚度分别是对振型函数与振型曲率的平方进行积分,其被积函数包括10项,为2项三角函数与2项双曲函数的二次展开式。该函数的积分是振动响应分析中最为繁杂的推导过程,是难于获得相应解析结果的主要原因。但由于双曲函数与三角函数的二次乘积均存在解析积分结果[22-23],因此对于除两端简支以外的其他边界条件,无论等直梁受集中力、均布力或是线性分布力作用,其振动响应的解析解均可获得,只是表达式的形式比较繁琐。
考虑到火箭减载结构主要提供质量和刚度约束效应,为研究减载结构的效果与设计方法,本文首先推导了带质量和弹簧约束悬臂梁的特征方程,并分析了不同附加质量和弹簧刚度对固有频率和弯曲振型的影响。其次根据特征值条件,创新性地提出了特征变换方法,将各阶广义质量拆分为50%的广义质量与50%的广义刚度除以固有频率平方之和,化简了广义质量积分的求解过程,获得了带约束悬臂梁广义质量和广义刚度的解析解,并验证了广义质量推导结果的正确性。最后给出了均布力作用下带约束悬臂梁振动响应的解析解,分析了根部弯矩、端部位移、速度和加速度放大系数的变化特征,总结了附加质量和弹簧刚度对减载效果的影响规律,并据此给出了火箭减载结构设计的建议。
本文通过特征变换方法,得到了不同质量和弹簧约束悬臂梁的振动响应解析解,丰富了结构振动理论,提供了便于结构优化设计的参数化分析方法。采用本文的解析方法可以连续分析设计参数对振动响应的影响规律,进行优化设计时可直接获得设计结果。而采用有限元方法需要建立各个参数取不同数值时的多个模型,间断分析各参数对振动响应的影响规律;进行优化设计时需要反复进行有限元模型的重构与迭代,优化效率和效果低于解析方法。
1 端部带质量和弹簧约束悬臂梁的模态
等直梁横向弯曲振动的位移通解w(x,t)为[1]
(1)

如图1所示,受均布正弦载荷psin(ωt)作用、端部带质量M和弹簧(刚度系数为K)约束的悬臂梁,其边界条件为
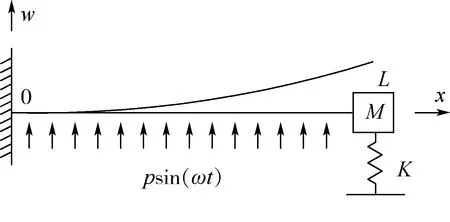
图1 端部约束悬臂梁的振动示意图Fig.1 Vibration schematic of cantilever beam with tip constraints

(2)
(3)
(4)
由固支端边界条件(式(2))可以确定:
(5)
由式(3)可得
(6)

(7)

1+cosλncoshλn+λn(cosλnsinhλn-
sinλncoshλn)/η=0
(8)
式(8)即为悬臂梁端部只有附加质量M时的特征方程,与Swaminadham和Michael[12]、王栋[13]、夏季等[18]所获得的结果一致。
将式(7)中的三角函数和双曲函数分别进行三阶泰勒展开,化简后可以得到特征值的近似特征方程为
(9)
由式(9)可以看出,当附加质量M增大时,η减小,导致λn减小,即梁的固有频率ωn降低;当附加弹簧刚度K增大时,ζ减小,导致λn增大,即梁的固有频率ωn增大。由此可知,对端部带质量和弹簧约束的悬臂梁而言,附加质量的增大降低结构的固有频率,此规律与Swaminadham和Michael[12]的数值结果规律一致;附加弹簧刚度的增大提高结构的固有频率。
特征方程式(7)的根可用数值方法求解。表1分别给出了梁在悬臂端无约束、有不同附加质量和弹簧约束时的特征值,其中硬、中等和软弹簧的刚度比分别取为ζ=0.03、ζ=0.1和ζ=0.3,大、中等和小质量的质量比分别取为η=0.2、η=0.5和η=2。
从表1可以看出:①对于一阶固有频率而言,只有梁悬臂端带硬弹簧和小质量约束时的特征值(见表1中黑体数据)高于无约束时的特征值,且带软弹簧和大质量的特征值(见表1中黑体数据)明显低于无约束时的特征值,其他3种状态的特征值均略低于且较接近无约束时的特征值。②对于二阶以上固有频率而言,梁悬臂端带弹簧和质量时的特征值均低于无约束时的特征值,弹簧硬度和附加质量对同阶固有频率的影响很小,小质量的频率略高,中等以上质量的频率略低。③附加弹簧刚度的增大只能提高低频段的固有频率,并且附加质量不能过大,附加弹簧刚度不能过小。④附加质量降低高低频段的固有频率,并且降低程度随着阶数的增加而变小。⑤在高频段由于以惯性力为主,附加弹簧的影响降低。因此,质量效应对固有频率的影响高于弹簧效应。

表1 端部带不同质量和弹簧约束悬臂梁的特征值λnTable 1 Eigenvalues λn of cantilever beam with different tip mass and spring constraints
由前述推导可知,端部带质量和弹簧约束悬臂梁的横向弯曲振型φn为[1]
(10)
式中:Sn=-An/Bn;λn为表1中对应不同附加质量和弹簧刚度的悬臂梁弯曲振动特征值。
由梁悬臂端无附加弹簧和质量时的前四阶振型(见图2(a))可见,悬臂端在一阶和三阶、二阶和四阶的振型值分别为1、-1。由梁悬臂端带中等附加弹簧和中等质量时的前四阶振型(见图2(b))
可见,与图2(a)相比,此时悬臂梁的一阶振型变化不大,二阶以上振型值随着弹簧刚度和质量的增大向零趋近。即增加端部约束后,约束点振型值的绝对值减小,中间位置的振型值变化较小。
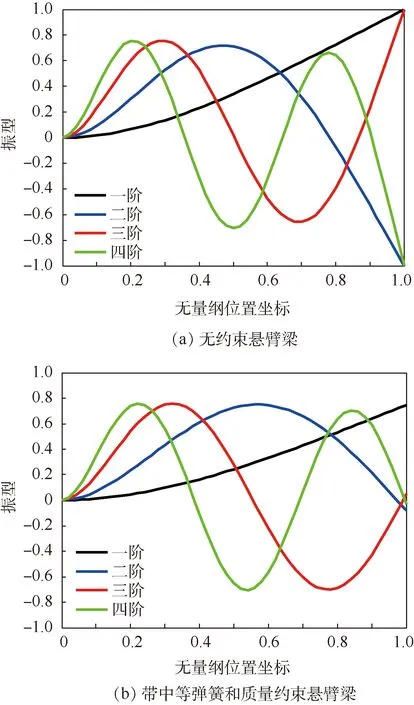
图2 悬臂梁的振型Fig.2 Vibration types of cantilever beam
2 端部带质量和弹簧约束悬臂梁的广义质量
由于梁的截面弯矩与振型曲率成比例,因此无量纲振型曲率φn与弯矩分布相关,其表达式可写为[1]
(11)
不同参数悬臂梁的振型曲率差别不大。由于附加质量和弹簧仅提供线位移约束,没有角位移约束,因此其对振型斜率和振型曲率的影响较小。
对于图1中的悬臂梁而言,其广义力是分布力的振型加权积分,是与外激励相关的非模态参数;其广义质量是质量分布的振型平方加权积分,是与系统相关、与外激励无关的模态参数。由于悬臂梁的广义质量解析计算比较繁杂,因此目前其振动响应没有解析解[1],更没有带质量和弹簧约束悬臂梁的振动响应解析解。
为了获得带约束悬臂梁广义质量的解析解,本文参照Timoshenko等[1]对于悬臂梁广义质量和广义刚度的定义,可得如图1所示悬臂梁各阶振型函数的广义质量mn为
(12)
广义刚度kn为
(13)

(14)
(15)
式中:解析积分项Nn为
2Sn(cosh(2λn)-cos(2λn))]
(16)
由此结果也可获得广义刚度kn的解析解为
(17)
式(14)~式(17)化简了双曲函数二次项解析积分问题,获得了简洁的广义质量和广义刚度的解析积分结果。但是本文提出的特征变换方法需要利用特征方程,仅限于特征值问题分析,不具备普适性,除非其控制方程与特征值问题类似。
在特征根已知的条件下,通过式(12)可以得到无量纲广义质量mn/m的数值积分结果,通过式(15)可以得到无量纲广义质量的解析积分结果。为了验证式(15)所获得广义质量解析解的正确性,将上述数值法和解析法得到的结果列于表2。在表2的6种状态中,采用这2种方法分别获得的广义质量,除第一阶因特征值的舍入误差和数值积分的计算误差而在万分位有微小差别外,其余三阶完全相同。由此证明了式(15)广义质量推导结果的正确性。对应于本文定义的振型,表2中无约束悬臂梁的各阶无量纲广义质量均为0.250 0,不同附加质量和弹簧刚度对三阶以上广义质量的影响小于2%,对二阶广义质量的影响小于9%。随着附加质量和弹簧刚度的增大,一阶广义质量均不同程度的增大。因此,可以只考虑附加质量和弹簧刚度对一、二阶广义质量的影响。
端部带约束悬臂梁广义质量和刚度解析计算问题的解决,为其振动响应的解析分析奠定了基础,是对结构振动理论的丰富和发展,所提出的特征变换方法也为振动响应问题的分析提供了一种新途径。

表2 端部带不同质量和弹簧约束悬臂梁无量纲广义质量的解析解和数值解Table 2 Analytical and numerical solutions of dimensionless generalized mass for cantilever beam with different tip mass and spring constraints
注:表格中“/”前数据为解析解,“/”后数据为数值解,无“/”栏中的解析解与数值解相同。
3 均布力作用下端部带质量和弹簧约束悬臂梁的振动响应
悬臂梁在均匀分布的横向稳态激励力作用下的强迫位移响应,可以采用振型叠加原理进行研究。设端部带质量和弹簧约束悬臂梁强迫振动响应的横向位移w(x,t)为[1]
(18)
沿悬臂梁上均匀分布的稳态激励力为psin(ωt)=(Q/L)sin(ωt),Q为均布力p的合力,则相应的广义力Fn可写为
(19)
式中:δn=[sinhλn-sinλn+Sn(2-coshλn-cosλn)]/(2λn)为均布力对应的广义力函数。
各阶振型所对应的平衡方程为[1]
(20)
去掉式(20)中的公共因子sin(ωt),并代入式(17),可以得到均布力作用下各阶振型的广义位移幅值Yn为
(21)
将式(21)代入式(18),可得对应的强迫位移响应为
(22)
式(22)为本文的核心研究结果,给出了均布稳态激励力作用下端部带质量和弹簧约束悬臂梁的强迫位移响应。
利用φn(λnx/L)|x=0=1,悬臂端的根部弯矩Mb可以通过对位移两次微分得到
(23)
端部无约束悬臂梁的静态根部弯矩为QL/2,考虑模态阻尼比ξ的根部弯矩放大系数βξ可写为
(24)
与端部无约束悬臂梁的端部静态位移响应Q/(8k)对应的位移放大系数βw为
(25)
当η→∞,ζ→∞时,ωn0=(λn0/L)2a,式(22)、式(24)退化为无约束悬臂梁的振动位移响应和根部弯矩放大系数:
(26)
(27)
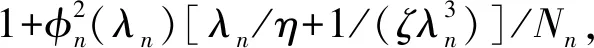
为了与Timoshenko等[1]得到的端部作用集中力Qsin(ωt)的响应结果进行比对,利用集中力的广义力为
(28)
由式(15)和表2可知,Nn0/λn0=0.5,φn(λn0)=(-1)n+1,悬臂梁端部的位移响应为
(29)
此结果与Timoshenko等[1]的解答一致,证明了推导结果是正确的。
4 悬臂梁端部位移和根部弯矩放大系数与减载效果
从图3(a)可知,与无约束的悬臂梁相比,不论附加质量大小和弹簧软硬,带质量和弹簧约束悬臂梁的动态根部弯矩一阶响应的谐振峰均降低。附加弹簧较硬时,低频段的载荷衰减效应较强,弹簧较软时,低频段的衰减效应较弱。衰减效果与附加弹簧刚度的相关性较强,与附加质量的相关性较弱。带附加质量和弹簧悬臂梁二、四阶的谐振峰高于无约束悬臂梁,有载荷放大效应;三阶的谐振峰低于无约束悬臂梁,也低于其各自的二、四阶谐振峰。在增加约束后,悬臂梁一阶的减载效果比较明显,对于附加中等以上弹簧的减载效果在5倍以上;二阶以上的减载效果不大。悬臂梁在各种约束情况下的根部弯矩放大系数曲线在一阶频率区域差别比较明显,从二阶频率开始逐渐靠拢,三阶以上基本一致。即不同附加质量和弹簧刚度对悬臂梁的低频段影响较大,对高频段的影响趋于一致。由此分析结果可知,减载结构设计时,只要控制等效弹簧在中等硬度(弹簧刚度大于悬臂梁等效刚度的10倍)以上,就能获得5倍以上的减载效果。即减载结构质量的影响低于弹簧刚度的影响,因此在进行相关设计时可以放宽对质量的要求。

图3 不同约束悬臂梁的根部弯矩和端部位移放大系数Fig.3 Amplification factors of root bending moments and tip displacements for cantilever beam with different constraints
从图3(b)可以看出,带不同质量和弹簧悬臂梁的静态和一阶端部动态位移的变化特征与其各自的根部弯矩相似,根部弯矩和端部位移只受附加弹簧刚度的影响。在二阶以上频率时,端部位移与根部弯矩的变化特征有明显差别:带不同附加质量和弹簧悬臂梁各阶次的位移谐振峰均低于无约束悬臂梁,并且其三、四阶谐振峰衰减更大;随着阶次增大,带不同附加质量和弹簧约束悬臂梁的谐振峰一直降低;在二阶以上高频衰减中,附加质量的影响占主导,附加弹簧刚度的影响可以忽略不计。由此特征可知,减载荷与减位移响应设计的异同之处在于:低频衰减都是采用附加弹簧约束的方法,并且2种动态响应参数的衰减率相近;但对于二阶以上的频段,随着附加质量的增大,动态位移谐振峰显著降低,而根部弯矩的谐振峰基本不变。即附加质量只能降低高频位移,不能降低高频弯矩载荷。
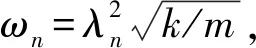
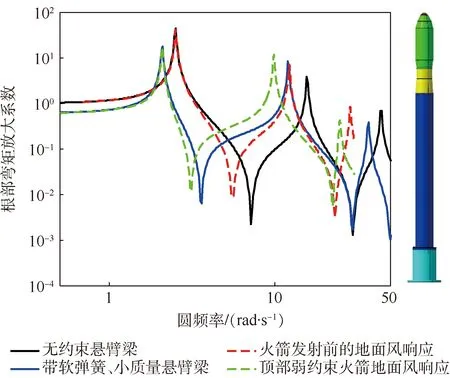
图4 不同约束时火箭模型和等直梁的根部弯矩放大系数Fig.4 Root bending moment amplification factors of rocket model and constant section beam with different constraints
5 悬臂梁各响应参数的放大系数

(30)
(31)
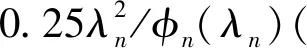
图5(a)、(b)分别给出了无约束悬臂梁、带中等弹簧和质量约束悬臂梁的端部加速度放大系数βa、端部速度放大系数βv、端部位移放大系数βw和根部弯矩放大系数βξ的计算结果。可以看出,βa、βv和βw曲线的变化规律有不同之处:端部加速度放大系数βa的谐振峰变化相对平缓,端部位移放大系数βw的谐振峰下降较快,端部速度放大系数βv谐振峰的变化介于两者之间。这3条曲线从一阶频率之前的交点后的间距逐渐增大。根部弯矩放大系数βξ的变化规律比较复杂,其曲线形状与βv、βa和βw3种曲线形状的差别较大,一、三阶反共振谷的差别最大;βξ的曲线在一阶频率范围内与βv的曲线接近;在二阶频率以后,对于悬臂梁状态,βξ的谐振峰低于且接近于βv,对于带中等质量和弹簧约束的悬臂梁,βξ的谐振峰低于且接近于βa。因此,根部弯矩高频分量的衰减程度介于加速度和速度之间,低于位移的衰减程度。结合工程经验可知,高频位移响应远小于低频位移响应,高频加速度与低频加速度在同一量级。在载荷分析中,只考虑一阶载荷通常是不够的,不能忽略高频载荷,并且需要通过分析与比较来确定所关注高频载荷的阶次。载荷响应分析阶次应介于速度和加速度的分析阶次之间,高于位移的分析阶次。但对于减载结构设计,由于一阶广义力远大于高阶广义力,因此主要关注静态和一阶根部弯矩。
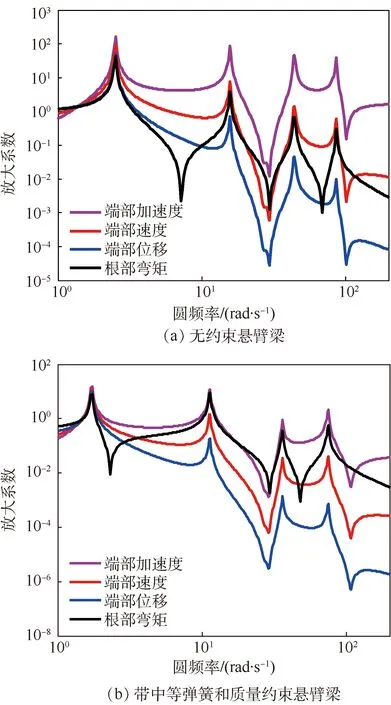
图5 悬臂梁的4种振动响应放大系数Fig.5 Four amplification factors of vibration response for cantilever beam
6 结论与讨论
1) 获取梁结构振动响应解析解的关键——特征变换方法
① 对于端部带弹簧和质量约束悬臂梁的振动响应而言,不论边界条件和特征方程复杂与否,其各阶特征值的解总可以采用数值方法获得。
② 振动响应解析解获得的基础是广义力和广义质量的解析积分结果。其中,分布力的广义力仅是双曲函数和三角函数一次项的积分,其解析积分计算并不困难;广义质量的解析积分是双曲函数和三角函数二次项的积分,计算比较繁杂。
③ 本文提出的特征变换方法,简化了推导过程,得到了广义质量的解析结果,为火箭减载结构的振动响应与减载设计分析问题奠定了理论基础。
2) 弹簧约束是影响火箭减载效果的主要因素
① 从带约束悬臂梁的振动响应分析结果来看,减载效果主要在一阶,二、四阶载荷响应有放大现象。
② 附加弹簧的刚度对静态和一阶载荷响应有明显影响,超过悬臂梁刚度10倍后减载效果超过5倍。
③ 附加质量的减载效果较小,减载设计时可以放宽对附加质量的限制。
④ 从不同振动响应参数的频率特性来看,位移、速度和加速度的高频衰减效应依次降低,根部弯矩的高频衰减特性介于速度和加速度之间,因此载荷响应分析阶次也应介于速度和加速度的分析阶次之间。
3) 等直梁在其他边界条件和载荷形式下的振动响应解析解
① 采用本文获得的均布力作用下带不同约束悬臂梁动响应解析解方法,还可得到集中力、线性分布力作用时的振动响应解析解,但得不到二次幂以上函数分布力作用时的振动响应解析解。
② 对于端部有转动惯量和角弹簧等角位移约束的悬臂梁,以及除悬臂梁之外的其他边界条件等直梁,其振型和振型曲率函数表达式的形式均相同,仅在各项函数的系数上有区别,并且每种边界约束类型下特征方程的数值解均可以获得。
③ 当端部约束为附加转动惯量和角弹簧时,广义质量和广义刚度的定义需要调整,将端部振型改为振型斜率。即使端部约束为线、角位移四项约束的组合,导致特征方程进一步复杂化,但也均可以利用本文的特征变换方法获得广义质量和振动响应的解析解。
