管内速度分布的不对称性对均速管流量计测量精度影响的数值研究

钟兴林，张文康，朱亚斌，杨雪峰

（四川大学 化学工程学院，四川 成都 610065）

0 引言

均速管流量计是基于皮托管流量计发展起来的一种新型差压式流量计，其目的是为了克服皮托管流量计因单点取样而对管内速度分布对称性的严格要求。通过采用如图1所示的在近管壁处的多点取压方法，均速管流量计可以应用于非对称性流速分布管段的流量测量，适用范围更大，测量精度也有所提高。因其结构简单，安装方便，价格低廉和节能的优点[1]，现已被广泛的应用于冶金、石化等工业计量中。

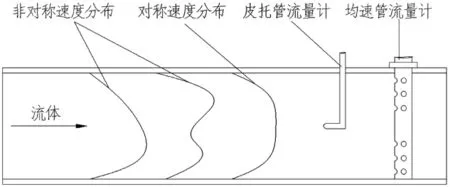
图1 均速管流量计取压方法示意图Fig.1 Schematic diagram of measurement method for averaging pitot tube

图2所示为均速管流量计检测杆的横截面，其均压原理是通过分布于管壁附近的多点取压孔将压强引入检测杆内部的均压腔，迎流面取压孔引入高压（冲压），侧面取压孔引入低压（静压），引入的各点压强在均压腔内平均后被引压管引出。

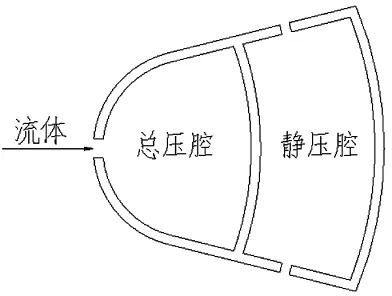
图2 均速管流量计横截面Fig.2 The cross section of averaging pitot tube

均速管流量计测量原理遵循伯努利方程[2-3]，设均速管流量计检测杆迎流取压孔处速度为U1(m/s)，压力为P1（Pa），检测杆侧流取压孔处的流速为 U2（m/s），压力为 P2（Pa），忽略摩擦阻力，流体高度差等因素，可得到：

式中：ρ是流体密度，kg/m3。

当迎流面流动稳定时取压孔处速度为零，可以简化得到：

式中：△P是总压P1和静压△P2之差，Pa。U2可视为管道流体的平均流速。

管道中流体体积流量的理论值为：

其中，A是管道横截面积，m2。

由于流体的黏性摩擦会造成一定的机械能损失，故实际值和理论值会有一定的差异，可以用流量系数K修正表示为：

实际的体积流量公式表示为：

其中流量系数K由多种因素共同影响，是测量探头速度系数、被测管道速度分布修正系数和管道安装干扰系数三部分的乘积[4]。其中速度系数可看作流量计在均匀流场中流速与输出差压之间关系的修正；速度分布系数是管道内处于充分发展流动时流速分布对平均速度测量影响的修正；干扰系数则是现场安装条件对流量测量影响的修正[5]。流量系数K的准确与否会直接影响流量测量的精度。工程应用时都是通过实验标定作为固定值应用于实际测量。

均速管流量计取样具有实际意义的前提是管道内的速度分布是对称稳定的充分发展湍流，各个取压孔的速度算数平均值近似等于管道截面的平均速度[1]，这是插入式均速流量计的测量精度取决于管道内流速分布的特点。一般而言，完全对称的速度分布是最理想的，但在应用过程中受实际情况的限制，并不能保证有足够长的直管段使流动达到充分发展，在现场直管段长度较短、上游又有弯管阻件导致流速分布复杂时，测量误差会较大[1，5]。

为了更深入地了解管内流速分布特点对流量系数的影响，本文对处于弯管后不同直管段位置和不同流速条件下的均速流量计内部流场进行了数值模拟，并分析了管内速度分布对均速管流量计的测量精度的影响。

这是我读过的亦舒最动人的小说。很多人都像小说中的女主角一样，觉得父母面目可憎，言语无味，可我们都忘记了，即使是现在垂垂老矣的人，也有过童年啊，他们也曾被父母捧在掌心，他们也曾有过胖嘟嘟的脸蛋和小手。所以，当你厌倦他们的时候，想想他们小时候吧，也许你会对他们多一些谅解和温柔。

1 数值模拟

1.1 物理模型和数值方法

计算选择检测杆有效长度为200mm的子弹头威力巴均速管流量计为物理模型；垂直于管道中心线、弯管平面插入；三对取压孔按照切比雪夫法分布[6]；阻塞比为8.9%，可忽略检测杆对管道内流速的影响；工作介质为常温空气，密度为1.225kg/m3，运动黏度为1.7894×10-5；弯管前直管段L0=20D，弯管后直管段长度L1=4D～11D，均速管流量计后直管段长度为L2=5D，图3所示为计算域弯管平面示意图，流速范围为6～30m/s，对应的雷诺数范围是 0.822×105～4.11×105。

图3 计算域示意图Fig.3 The computational field diagram

利用前处理软件ICEM对计算区域进行网格划分，采用非均匀网格，并对网格进行优化，检测杆内部空腔采用较密集的网格，最小网格尺寸为0.2mm，对靠近流量计的一段管道进行加密，最小网格尺寸为1mm，以保证数值模拟的精度。图4是整个流场的三维仿真模型示意图。

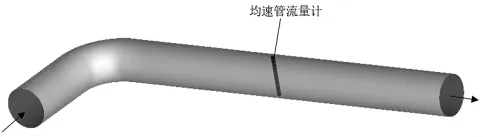
图4 计算域的三维仿真模型Figure.4 Three-dimensional simulation model of computational field

用Fluent流体力学软件进行数值模拟，用有限体积法对控制方程进行离散，模型选用标准kepsilon湍流模型，近壁区采用标准壁面函数法，入口条件采用Velocity-inlet，出口条件采用Pressure-outlet。

1.2 控制方程和湍流模型

求解各个算例的的流体动力学特性可以用流体力学基本方程[4，7]。

连续性方程为：

动量守恒方程为：

有效黏度系数μef是分子黏度μ和湍流运动黏度系数μt之和，即：

湍流运动黏性系数是由k-ε确定：

本文采用的湍流模型是标准k-ε模型，标准湍流模型的湍动能和耗散率由以下方程确定：

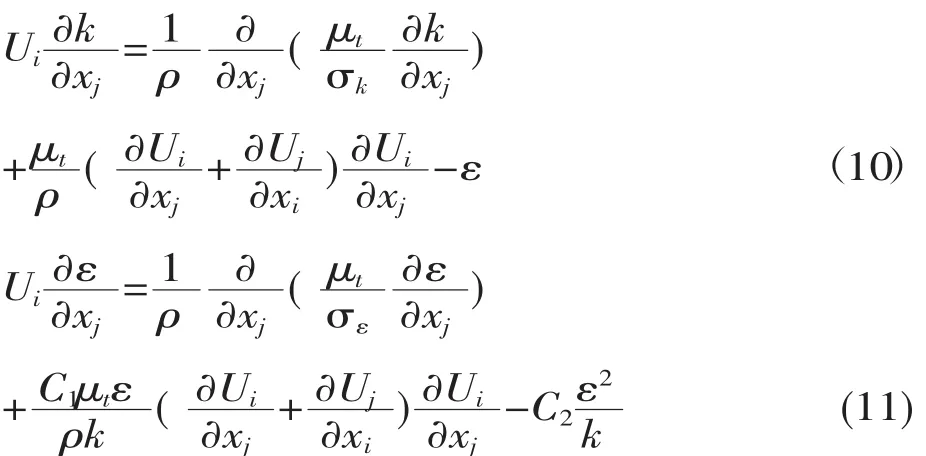
其中，各系数的取值分别为C1=1.44，C2=1.92，σk=1.0，σε=1.3，Cμ=0.09。

1.3 边界条件

入口处：给定入口水平速度Ux，其他两个方向速度为：Uy=Uz=0；

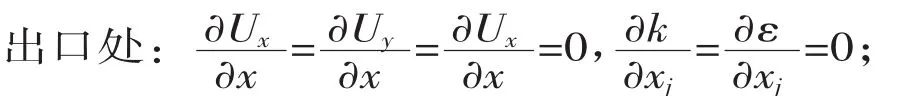
管壁处：采用无滑移边界条件，即Ux=Uy=Uz=0；

当管道内达到充分发展湍流之后，水平方向的速度剖面分布[8]为：

式中，Umax是管道中心速度，y是管道内部任意点距离管中心的距离，R是管道半径，指数n与雷诺数Re有关。

1.4 仿真结果和讨论

在不同直管段位置和不同流速的条件下，引用标准k-ε模型，模拟得出了均速管流量计附近的速度场和压力场。

图5所示是入口流速为15m/s的条件下，直管段内充分发展的湍流（L0=0，无弯管附件，L1=20D，L2=5D） 的模拟结果。由速度云图（图5a）看出，在流量计迎流面上没有开孔的位置，流速骤然下降并接近于零，在取压孔处的速度虽然有所下降，但并不为零。根据充分发展湍流的速度分布可知，管中心处的速度最大，检测杆上半部的三个取压孔的速度分别为6.411m/s、2.536m/s、-5.653m/s，提示总压腔内的流体不是静止的，流体从中心附近的两个取压口流入，从近壁处的取压孔流出。检测杆下半部的三个取压孔的流速分别为6.497m/s、2.416m/s、-5.624m/s，与上半部分基本对称。压力云图（图5b）则显示了检测杆内部压力的差异。压腔内的压力是由取压孔引入的压力平均之后得到的结果，总压腔是正高压，为184.233Pa，静压腔是负低压，为-55.394Pa。

图5 充分发展湍流下均速流量计附近的速度云图（a）和压力云图 （b）Fig.5 Velocity contour(a)and pressure contour(b)near the averaging pitot tube of full development turbulence

图6给出了直管段充分发展湍流条件下，均速管流量计前0.25D处的纵轴截面上的速度分布，可以看出在此情形下的湍流流形是对称的、均匀的。

图6 充分发展湍流的速度分布Figure.6 Velocity distribution of full development turbulence

对于受弯管影响的湍流（L0=20D，有弯管附件，L1=4D～11D，L2=5D）的情况，图7给出的是入口速度为15m/s时均速管流量计处于弯管后4D位置的模拟结果的云图。从速度云图（图7c）看出速度分布明显不对称。靠近管中心的取压孔附近的流速分别为 4.005m/s、2.655m/s，3.53m/s、3.715m/s，而靠近管壁的取压孔附近的流速为-1.123m/s、-1.339m/s；由取压孔引入的压力也出现了较大变化，总压腔内压强为172.492Pa，静压腔为-44.958Pa。云图也展示了速度和压强的等值区域受弯管影响而产生的变化。

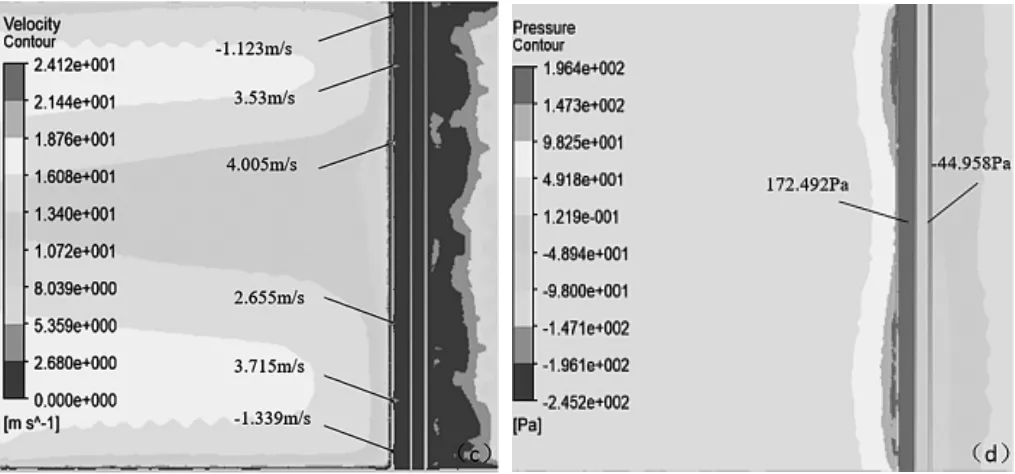
图7 受弯管影响湍流在均速流量计附近流场的速度云图（c）和压力云图（d）Fig.7 Velocity contour(c)and pressure contour(d)near the averaging pitot tube of turbulence affected by bending pipe

处于弯管后的均速管流量计前0.25D处纵轴截面上的速度分布如图8所示。纵坐标为纵轴截面径向上点的位置，横坐标为各点的速度，曲线代表了均速管流量计处于弯管后不同位置时测量的流体的速度分布。可以很明显看出在弯管下游有很长一段范围内，速度分布是中间低，两侧高，中间的速度逐步增大，到11D处仍然是外侧的速度大于内侧的速度，之后再继续发展。

表1列出的是根据模拟的差压数据计算得到的均速管流量计的流量系数K。可以看出，处于弯管后的均速管流量计测得的流量系数与对称分布的充分发展湍流下得到的流量系数存在一定的偏差，表明管内速度分布的不均匀性对测量精度的影响，在实际应用中应该加以修正。

图9是不同流速条件下，检测杆位于弯管后4D～11D距离时的流量系数的模拟结果。可以发现，有弯管影响时的流量系数均高于充分发展湍流情形下的值，这是速度分布的不对称性导致的结果。因此，在均速管流量计的应用上，当测量位置处于弯管后一定的距离内，应对流量系数进行修正，否则会导致测量结果的偏差。

图8 均速管流量计前0.25D处纵轴截面上的速度分布Fig.8 Velocity distribution on longitudinal axis section of averaging pitot tube

表1 不同情形下的流量系数K值和相对偏差值Tab.1 Flow coefficient K value and relative deviation value in different cases

图9 各情形下的流量系数K值Fig.9 Flow coefficient K value in each case

2 结语

本文对弯管后不同直管段位置和不同流速下的均速管流量计的流场进行了三维数值模拟，模拟得出了不同情况下检测杆内部的流动情况和管内速度分布的不对称性对均速管流量计测量的影响。得出了以下结论：

1） 均速管流量计垂直安装于弯管平面后，在弯管后4D～11D这段距离内，检测杆前纵轴截面上的速度呈现出“中间低，两边高”的规律。

2）弯管引起的管内速度分布的不对称性对流量测量精度的影响较大，建议对弯管后11D内安装的流量计进行流量系数修正。

3）数值模拟是研究均速管流量计检测杆的内部流动和测量精度的一种很好的手段，可以监测到实验难以提供的流场内部细节，其研究结果对深入了解均速管流量计和管道内部流场的特点有一定的应用价值。