基于巴克豪森效应预测烧伤齿轮显微组织的变化

(北京工业大学 精密测控技术与仪器工程技术研究中心,北京 100124)

随着社会的进步和科学技术的发展，齿轮作为传动的基础构件，其品质关系到生产效益和使用的安全性，所以必须对齿轮的品质进行严格控制。齿轮在进行磨削加工时，由于去除材料的厚度较薄，切削带走的热量很少，所以大部分的热量会传入至被磨削材料的内部，同时由于磨削加工的速度比较快，热量来不及传入材料的更深处，只能聚集在材料的表面。磨粒磨削点的温度通常可达到1 000 ℃以上，材料表层的局部温度很高，超过相变温度，表面将会出现热损伤和热变形，甚至会出现裂痕和断裂等损伤，严重影响了材料表面品质和加工的精度，故对齿轮实施安全检测是很有必要的。无损检测作为材料品质的重要保障环节，越来越受到人们的关注。在工业生产检测中，常用的无损检测方法主要有超声检测[1]、射线检测、渗透检测、磁粉检测和涡流检测等[2]。这些传统的检测技术在事故预防、品质控制和安全保障等方面发挥了重要作用，但是此类检测方法存在一些不足，如超声检测难以检查表面粗糙、形状不规则，小、薄或非均质的材料，并且很难定量表征缺陷等。涡流检测[3]对铁磁性材料进行磨削烧伤检测时灵敏度不高，结果显示不直观，对复杂零件几何外形引起的边缘效应较为敏感，容易产生虚假结果。射线检测对人体有辐射危害，并且射线对金属的穿透能力有限，测量范围为表面以下几微米到十几微米，因而具有一定的局限性[4]。巴克豪森噪声(Magnetic Barkhausen Noise，MBN)检测技术是20世纪八九十年代发展起来的无损检测技术，可实现对铁磁材料的硬度、应力的检测[5-6]，并可对材料的显微组织、硬度、表面状态做出分析和评价，具有巨大的应用潜力。典型的MBN特征值有均方根(RMS)[7]和MBN信号能量[8],而现在大多是从MBN信号包络线上提取特征值，比如峰值、峰值的位置和半峰宽[9]。然而使用MBN特征参量来定量预测材料特性是一项非常具有挑战性的工作，单一的MBN特征参量与烧伤齿轮之间并非存在良好的线性关系，主要原因是MBN受微观结构和残余应力等诸多因素的影响[10]。为了增强MBN作为无损检测工具的可靠性，笔者建立了自适应神经模糊推理系统(ANFIS)，以对MBN信号的包络与切向磁场的关系曲线上提取的特征参量进行处理。试验结果表明，即使在特征参数及其对应关系非常复杂且呈非线性时，提出的信号处理方法也能够建立MBN信号的特征值与烧伤齿面微观金相马氏体深度间的准确对应关系，进而对烧伤齿轮进行在线无损检测。

1 巴克豪森噪声检测装置

巴克豪森噪声信号检测原理和装置外观如图1所示，装置由信号发生器、功率放大器、U型磁轭、激励线圈、信号采集线圈、霍尔元件、示波器以及上位机等组成[11-12]。

图1 巴克豪森噪声信号检测原理和装置外观

巴克豪森装置检测流程为：信号发生器发出正弦波电信号，经功率放大器对信号进行放大，信号流经激励线圈，当通有电流的激励线圈经过U型磁轭的时候，磁轭中间会产生交变磁场，烧伤齿轮在交变磁场中会产生一系列不连续的脉冲信号，即MBN信号。通过信号采集线圈采集到MBN信号，霍尔元件可以采集切向磁场的信号，最后将采集到的信号通过示波器传输到计算机上进行后续的信号分析。

2 试样制备与试验方法

2.1 试样制备

试样采用法士特变速箱齿轮制作，齿轮试样实物如图2所示，为了方便检测,使用线切割机将齿从齿轮根部切开。

图2 齿轮试样实物

为了模拟齿面的磨削烧伤过程，采用Nd∶YAG固体激光器对齿面进行不同程度的烧伤，选用光斑直径为4 mm，正离焦方式，离焦量为16 mm，激光能量分别为3.8，14.4，26.0，28.9，31.2，33.0，35.3，42.2 W·s。由于激光辐射在齿面形成的烧伤斑直径只有4 mm左右，为了提高材料的利用率，在齿宽1/4和3/4处，齿高为1/2的地方进行激光烧伤处理。图3为不同激光能量烧伤之后的试样外观，图中的圆点就是激光烧伤之后形成的烧伤斑。

图3 不同激光能量烧伤后的试样外观

对试样进行MBN信号检测之后再进行金相试验，金相试样制作的流程为取样→镶嵌→磨光与抛光→侵蚀→观察照相等5个步骤。当金相试样制成之后，使用金相显微镜确定烧伤齿面的马氏体深度。图4为不同激光能量烧伤齿轮的显微组织截面。图中白色部分为马氏体组织，可以看出随着激光能量的增大，马氏体深度也在变深。

图4 不同激光能量烧伤齿轮的显微组织截面

为了验证巴克豪森效应可以预测烧伤齿轮显微组织变化的方法可以应用到实际烧伤齿轮的检测上，试验采用MM1320磨床，砂轮采用单晶钢玉砂轮，由于齿轮是完整的，所以磨削方式采用接触顺磨，磨削的部位是齿顶附近。工件位置不变，磨削深度是3 μm，砂轮的速度分别为15，20，25 m·s-1。通过改变砂轮的转速形成不同程度的烧伤。实际烧伤试样的外观如图5所示。

图5 烧伤试样外观

2.2 磁巴克豪森噪声检测及信号分析

测量之前用退磁器对试件进行退磁处理，确保每一个试样的初始磁状态保持一致。采集MBN信号时，使用的激励电压是6 V，根据电磁趋肤深度效应，低频可以从更大深度的材料处收集并记录信息，所以激励频率分别选择5,8,10 Hz对烧伤齿轮进行检测。通过采集线圈和霍尔元件可以采集到巴克豪森噪声信号MBN(t)和切向磁场信号H(t)，然后通过示波器将数据传输到上位机。采集到的MBN原始信号如图6所示，图中脉冲信号就是MBN信号，而正弦波形是切向磁场。

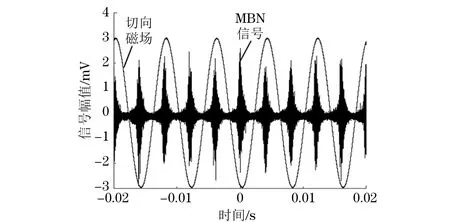
图6 MBN原始信号

采用MATLAB软件对MBN原始信号进行处理，由于试验过程中会有仪器振动和环境的干扰，首先选择10 kHz～70 kHz的带通滤波对MBN信号进行滤波;其次通过滑动平均的方法得到MBN信号的包络线，最后以切向磁场信号为横坐标，MBN信号的包络线为纵坐标画出MBN信号的包络与切向磁场的关系曲线(见图7)。通过MBN信号的包络与切向磁场的关系曲线提取MBN信号的特征值(峰值Mmax,峰值对应的切向磁场强度，50%峰值处对应的半峰宽值)。

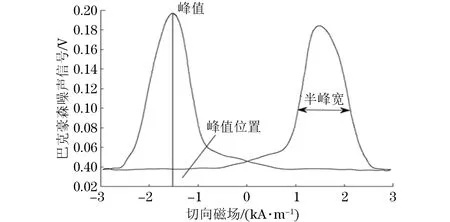
图7 从MBN信号的包络与切向磁场的关系曲线提取的特征值

2.3 烧伤齿轮马氏体含量ANFIS预测模型

通过建立ANFIS(自适应模糊神经网络)预测模型预测金相马氏体组织深度的改变，图8为ANFIS的结构图，ANFIS系统结构由5个不同的层组成[13]，每层节点都会生成输出，作为下一层的输入，其中x,y,z代表了MBN的特征参量是ANFIS预测模型的输入，F代表了烧伤齿轮马氏体含量是预测模型的输出。

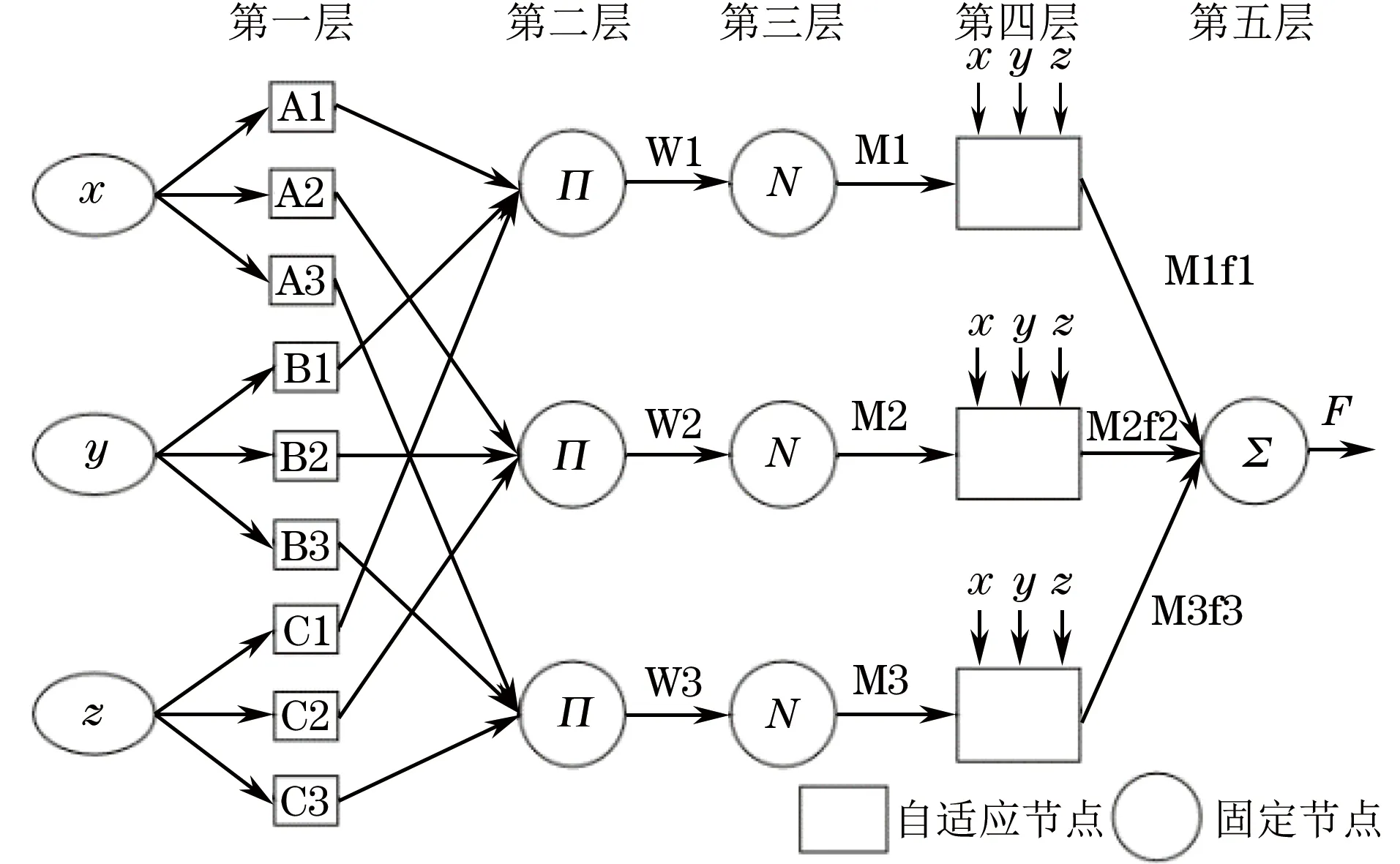
图8 自适应模糊神经网络的结构图

第一层：对输入MBN信号的特征值采用式(1)进行模糊化。

(1)

式中：Ai,Bj-3和Ch-6为模糊集;Ai(x)为隶属函数，这里选择的是高斯函数。

第二层：该层节点个数为规则数，规则的适用度数为ki，如式(2)所示。

N2,i=ki=Ai(x)Bi(y)Ci(x),i=1,2,3

(2)

第三层：每个规则的强度由层节点评估，采用式(3)进行归一化计算。

(3)

第四层：用式(4)计算节点对应的各规则的输出。

N4,i=ifi=i(pix+qiy+giz+ri),

i=1,2,3

(4)

式中：fi为Sugeno型模糊系统的后项输出函数。

第五层：仅有一个节点，所有第4层信号的总和作为系统的输出,如式(5)所示。

(5)

该模型采用的是反向传播算法与最小二乘算法相结合的混合算法来训练相关的参数。

3 测试结果讨论

使用OLYMPUS CK40M显微镜对烧伤齿面进行组织观察和定量分析。得到MBN信号特征值与试样金相组织中马氏体深度之间的关系(见图9)。

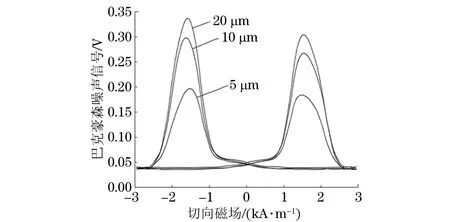
图9 MBN信号特征值与马氏体深度的关系曲线

在激励频率为5 Hz时,MBN信号特征值与马氏体深度的关系如表1所示。

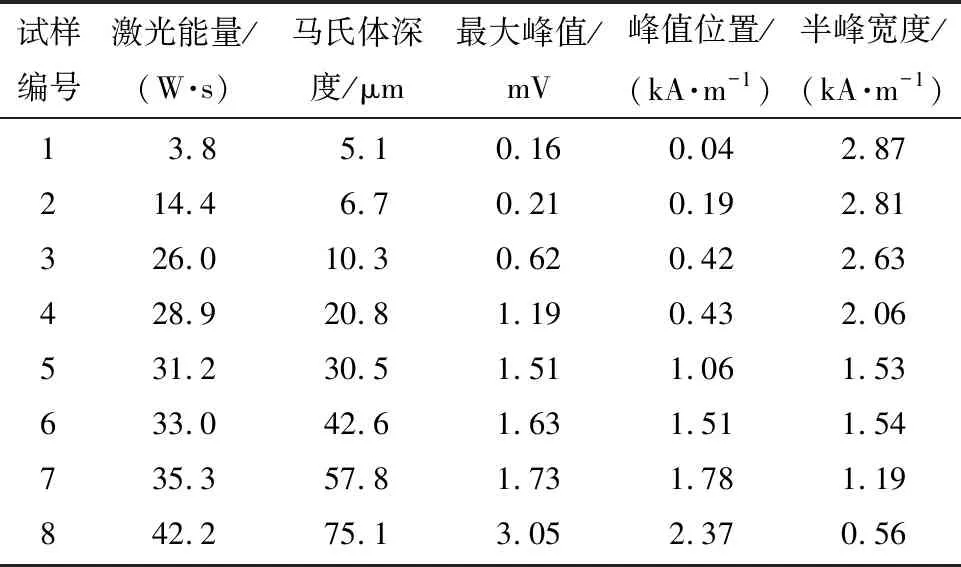
表1 激励频率为5 Hz时MBN特征值与马氏体深度的关系

在激励频率为8 Hz时,MBN信号特征值与马氏体深度的关系如表2所示。

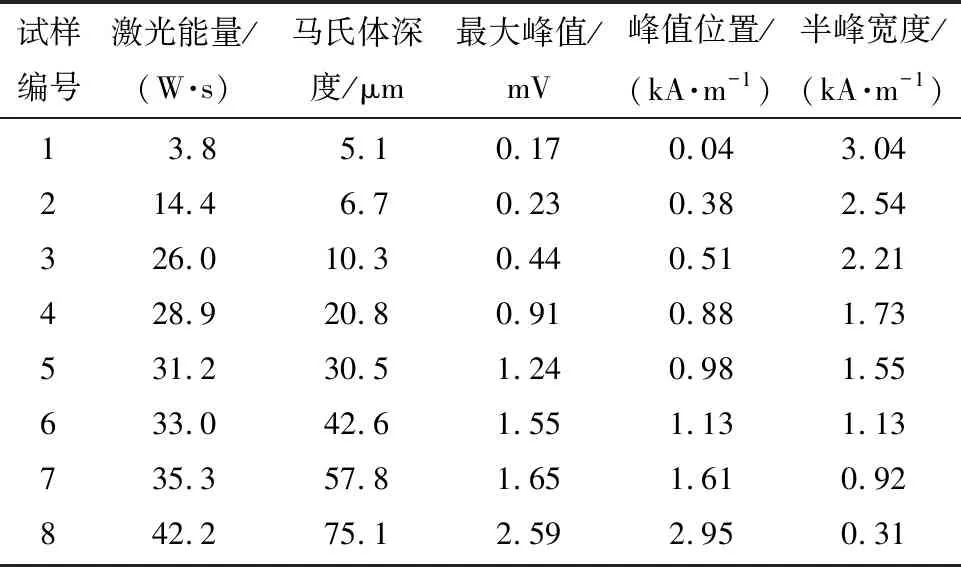
表2 激励频率为8 Hz时MBN特征值与马氏体深度的关系

在激励频率为10 Hz时，MBN信号特征值与马氏深度的关系如表3所示。

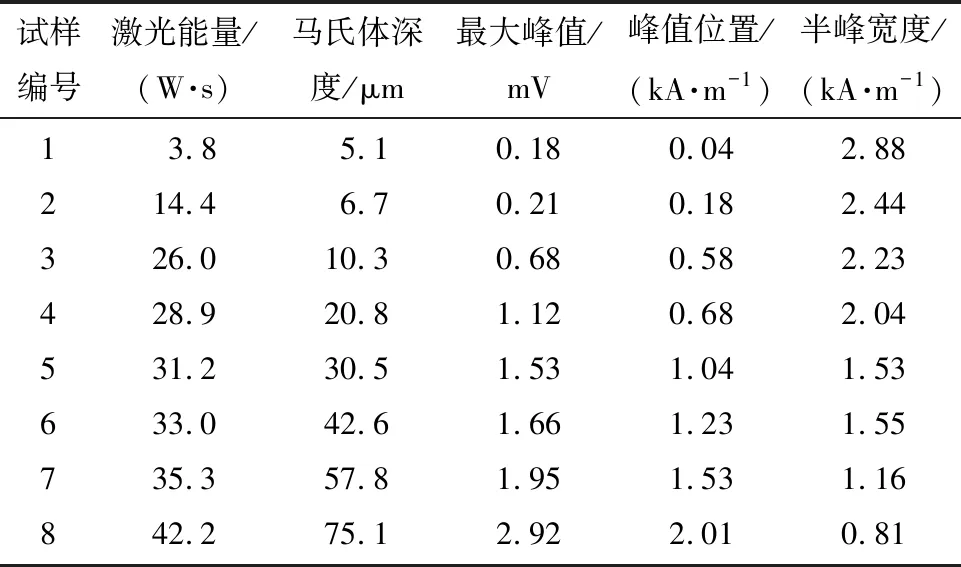
表3 激励频率为10 Hz时MBN特征值与马氏体深度的关系

根据表1～3中的数据，可得到不同激励频率下MBN信号特征值与马氏体深度的关系曲线(见图10)。

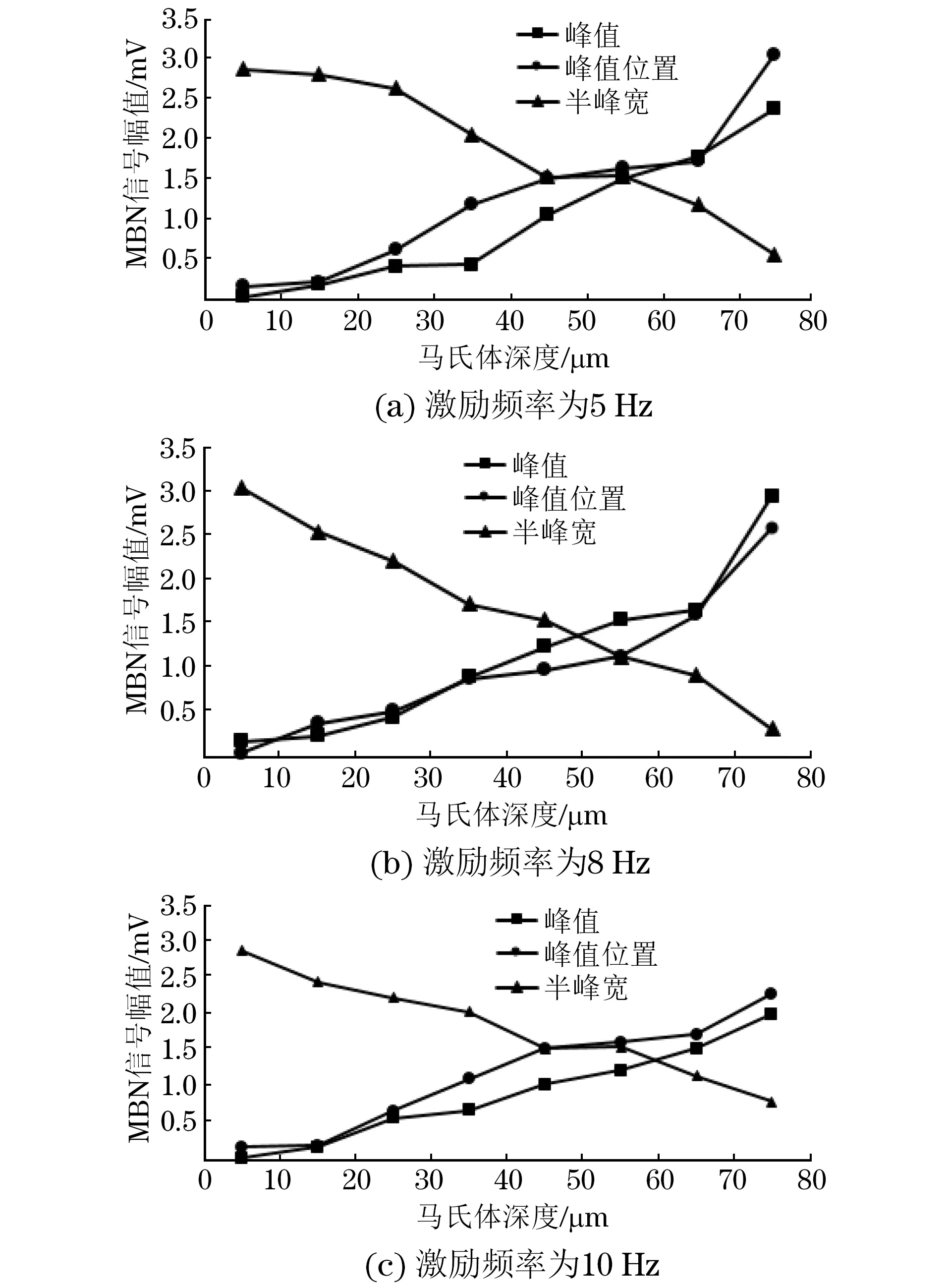
图10 不同激励频率下MBN信号特征值与马氏体深度的关系曲线

从图10可以看出，随着马氏体深度的增大，MBN信号峰值以及峰值所对应的切向磁场随之增大，而MBN信号的半峰宽随着马氏体深度的增大而减小。由于激光的能量很高，能够瞬间达到材料的相变温度，但持续时间很短，在空气中很快就能冷却，所以会形成针状马氏体。通过上述试验数据可以看出，随着激光能量的增大，马氏体的深度也不断增大。从图10可以看出，单一MBN特征参量与马氏体深度之间并非存在良好的线性关系。因此，引入ANFIS模型对MBN信号进行预处理，模糊推理能够很好地表达大脑的推理机制，神经网络具备自学习的能力，而自适应神经模糊推理系统把两者的优点结合到一起。将烧伤齿轮数据库分成两组，选择5 Hz和8 Hz的数据进行训练，用10 Hz的数据进行验证，随后对预期误差目标、训练次数进行调整，使预测模型更加合理。通过拟合优度R2和均方根误差RMSE来对ANFIS预测模型进行精度评价，通过图11中实际马氏体深度与预测马氏体深度的对比，可以得到R2=0.964 1，RMSE=16.981 7。因此，ANFIS预测模型具有高度准确性，而且预测数据与试验数据匹配度很高。

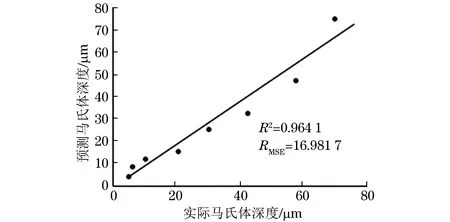
图11 使用ANFIS预测马氏体深度回归关系

在激励频率为10 Hz的情况下,利用ANFIS预测模型对实际烧伤试件进行检测，MBN信号特征值与砂轮转速之间的关系如表4所示。

根据表4中的数据，可得到激励频率为10 Hz时MBN信号特征值与砂轮转速之间的关系曲线，如图12所示。

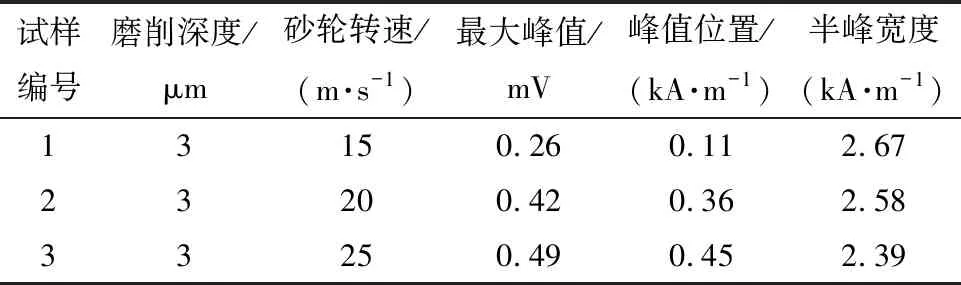
表4 激励频率为10 Hz时MBN特征值与砂轮转速之间的关系

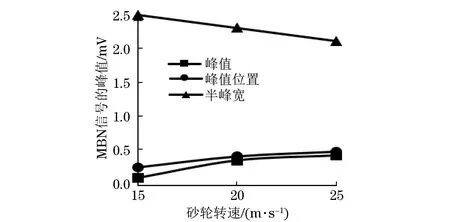
图12 激励频率为10 Hz时MBN信号特征值与砂轮转速之间的关系曲线

从图12可以看出，随着砂轮转速的增大，MBN信号峰值以及峰值所对应的切向磁场随之增大，而MBN信号的半峰宽随着砂轮转速的增大而减小。随着砂轮转速的增加，单位时间内经过齿轮表面的磨粒数变多，磨粒与齿轮表面的摩擦增快，磨削温度升高，最后导致齿轮磨削烧伤。使用已经建立的ANFIS模型对MBN信号进行预测处理，砂轮转速为15 m·s-1时，预测的马氏体深度为6.9 μm,砂轮转速为20 m·s-1时，预测的马氏体深度为8.5 μm，砂轮转速为25 m·s-1时，预测的马氏体深度为9.7 μm。上述数据证明了齿轮有轻微的烧伤，因此提出的基于巴克豪森效应预测烧伤齿轮显微组织变化的方法可以应用到实际中。

4 结论

(1)MBN信号对烧伤齿轮中微观结构变化非常敏感。结果表明，MBN信号的包络与切向磁场的关系曲线的峰值和峰值位置会随着烧伤齿轮微观金相组织中马氏体深度的增大而增大，而MBN信号的包络与切向磁场的关系曲线的半峰宽随着烧伤齿轮微观金相组织中马氏体深度的增大而减小。

(2)为了提高磁性巴克豪森无损检测的可靠性，采用ANFIS进行MBN输出处理，设计出专业的无损检测系统，仅使用MBN峰值，峰值位置和半峰宽就可以准确预测烧伤齿轮微结构中的马氏体深度。

(3)通过ANFIS模型处理之后消除了激励频率对MBN输出的影响，能够准确地获得烧伤齿轮的马氏体深度。

(4)使用训练好的ANFIS模型处理实际烧伤的齿轮，能够准确地获得实际烧伤齿轮马氏体深度，可以对其烧伤程度做出判定。