非接触空气耦合超声谐振法测厚

(1.南昌航空大学 无损检测技术教育部重点实验室,南昌 330063;2.日本探头株式会社,横滨 2320033)

超声谐振法是超声检测中一种常用的测厚方法，超声测厚不仅局限于测量出物体厚度这种简单的几何问题，还能通过所测厚度的变化，及时分析材料内部的变化。超声谐振法因为具有可测量下限小，测量精度高等优点，被广泛应用于厚度的检测中[1-3]。传统的接触式检测时使用的液体或固体耦合剂会给试件带来二次污染与损伤，而空气耦合超声检测具有非接触、非浸入、非破坏以及易实现自动化等特点。因此，空气耦合超声在复合材料、钢筋混凝土、钢板以及锂电池等材料的检测中得到了很好的研究和应用[4-8]。笔者提出了非接触空气耦合谐振测厚技术，简单地介绍了非接触式空气耦合超声谐振法测厚的优点、原理以及检测方式，使用不同厚度的测试体验证了谐振频率与测试体厚度的关系，并对由铝板制作的三角形凹槽、平行凹槽以及圆形凹槽等不同形状的凹凸表面进行谐振测厚试验，验证了空气耦合超声谐振法测厚的有效性和实用性。

1 谐振法测厚原理

在空气耦合超声检测中，超声波在试件中的往返透射率仅有接触法或者水浸法的1/10000[8]。当试件的厚度为λ/2(λ为波长)的整数倍时，试件下界面的反射波与入射波互相叠加而形成驻波时，试件会在厚度方向产生谐振(见图1)，声波能量的透射率从而发生很大变化，这就是非接触式空气耦合超声谐振法测厚的原理，测厚公式见式(1)，(2)。检测时，通过对接收到的声波谐振信号进行FFT(快速傅里叶变换)便可获得谐振频率，这样就可以计算出发生谐振的声波波长以及检测试件的厚度。

(1)

c=fλ

(2)

式中：c为被检测材料的声速；f为声波谐振频率；T为试件的厚度；n为半波长的倍数。

当n=1时，所得的f1为基本谐振频率，即谐振发生在半波长的时候；当n=2,3,4，…时，谐振发生在半波长的n倍，fn为谐振发生在半波长的n倍时的谐振频率。相邻2个谐波共振频率之差等于基本谐振频率，即

fn+1-fn=f1

(3)

当知道任意2个相邻谐波谐振频率之后，厚度为

(4)

图1 声波在试件内的谐振示意(声波波长等于测试体厚度的一半时)

2 测厚试验方法

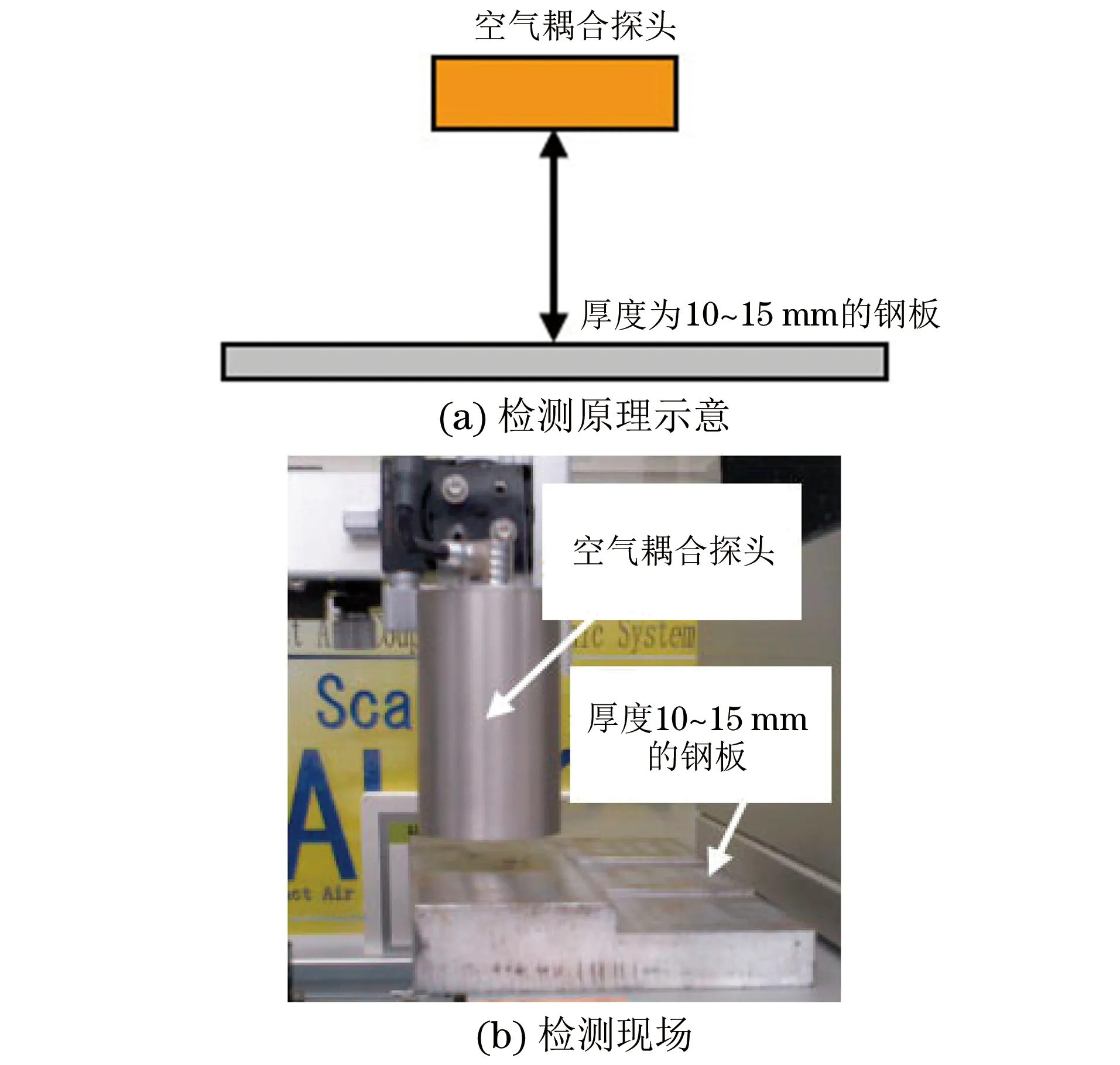
图2 非接触空气耦合超声谐振法测厚原理示意及检测现场

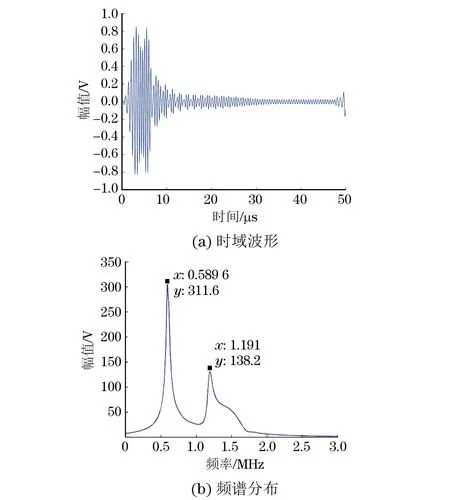
图3 5 mm厚钢板谐振试验接收到的时域波形和频谱分布

采用型号为JPR-600C的超声发射接收器和高灵敏度空气耦合专用超声探头，探头的中心频率为600 kHz，晶片直径为20 mm。使用探头架将探头垂直安装在厚度为5 mm钢板的表面，并保持一定距离，最后使用JPR-600C发射的电压为100 V，波数为30，中心频率为600 kHz以及调频比为1.2的线性调频波，让声波垂直入射到试件中，检测原理示意及检测现场如图2所示。对5 mm厚钢板进行谐振试验后接收到的时域波形如图3(a)所示，对波形中来自钢板内部发生若干次反射产生的反射回波进行傅里叶变换，得到的频谱分布如图3(b)所示。从图3(b)中可以看到频率为589.6 kHz和1.191 MHz的2个谐振峰，其中频率589.6 kHz与根据测试体厚度计算出的一阶基本谐振频率590 kHz接近，所以可以确认589.6 kHz为基本谐振频率，1.191 MHz为二阶谐振频率。分别对厚度为10，11，12，13，14，15 mm的钢板进行试验，得到其实际谐振频率、理论谐振频率以及根据式(4)计算出的厚度，如表1所示。由表1可知，其谐振频率随厚度的不同而变化，且根据检测出来的谐振频率可以计算出试件的厚度，误差在0.2 mm以内。接下来使用中心频率为500 kHz的探头测量了厚度为6 mm的钢板，使用频率为750，960 kHz的探头分别测量厚度为3，4，6 mm的钢板，结果如表2所示，试件厚度误差都在0.2 mm以内。

表1 不同厚度钢板的实际谐振频率、理论谐振频率以及计算出的厚度

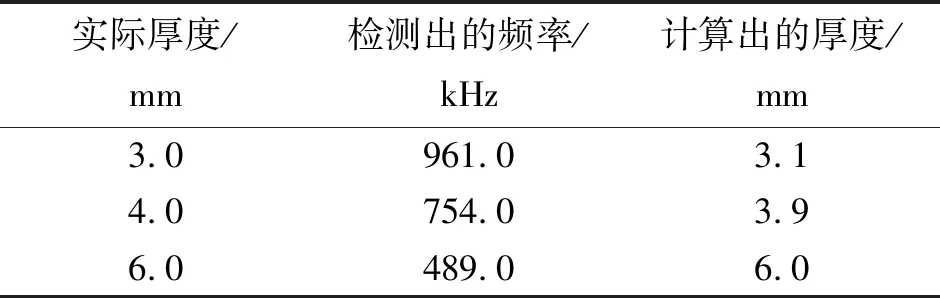
表2 厚度为3,4，6 mm钢板的测量结果

3 多种厚度及多种形状试件的测厚试验

在实际工程中，如果管道内部发生了壁厚减薄的情况，那么其表面不会是平坦的规则形状，而是存在凹凸不平的不规则形状。所以在铝板(声速为6 320 m·s-1)上制作了平行凹槽、三角形凹槽和圆形凹槽测试体，为了对比，测试体上留有厚度为5.5 mm的平面部分，三种凹槽的厚度结构示意如图4所示，以0.5 mm的深度设定了各自的凹槽，平行凹槽和圆形凹槽的间距为20 mm，三角形凹槽的间距为3 mm。使用超声发射接收器发射了电压为100 V，波数为10，频率为800 kHz，调频比为1.2的线性调频脉冲串信号。探头使用中心频率为800 kHz，晶片直径为20 mm，振动面为平面的高灵敏度空气耦合超声专用探头，使用谐振法对测试体进行厚度测量试验，测试体的整体结构示意如图5所示。

图4 不同凹槽形状测试体的结构示意

图5 测试体的整体结构示意

3.1 对平面凹槽测厚

对图4所示测试体的平面凹槽(厚度为5.5 mm)进行谐振法测厚试验，并对来自测试体内的波形进行FFT变换，图6为平面凹槽谐振法测厚试验得到的频谱分布。可以看到，图6中存在2处频率分别为0.563 MHz和1.151 MHz的谐振波峰，其中0.583 MHz处为声波产生的一阶谐振基本频率，1.151 MHz为声波产生的二阶谐振频率。根据式(4)对应计算出测试体的厚度为5.53 mm，厚度测量正确。

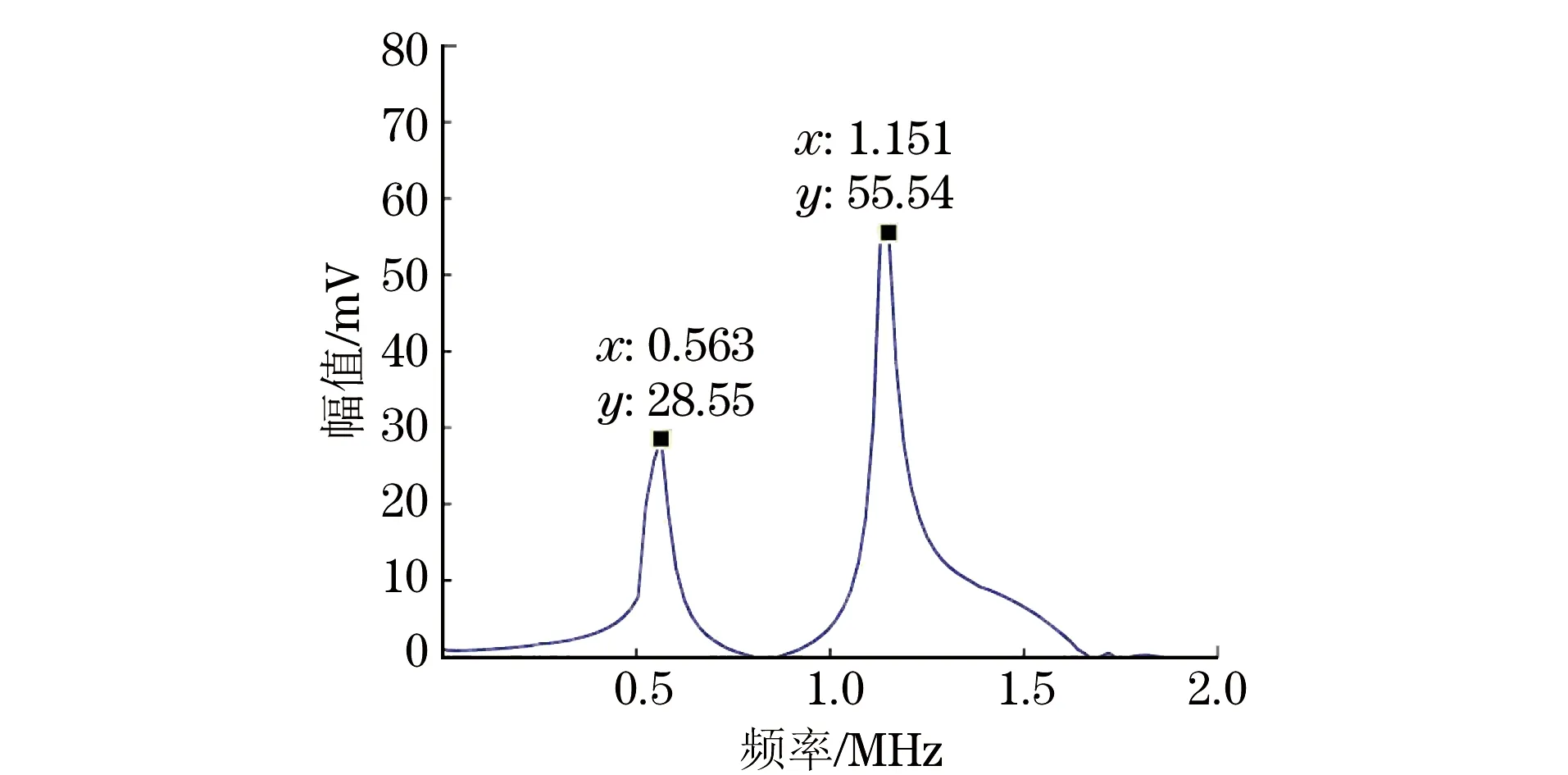
图6 平面凹槽谐振波形的频谱分布

3.2 对平行凹槽测厚

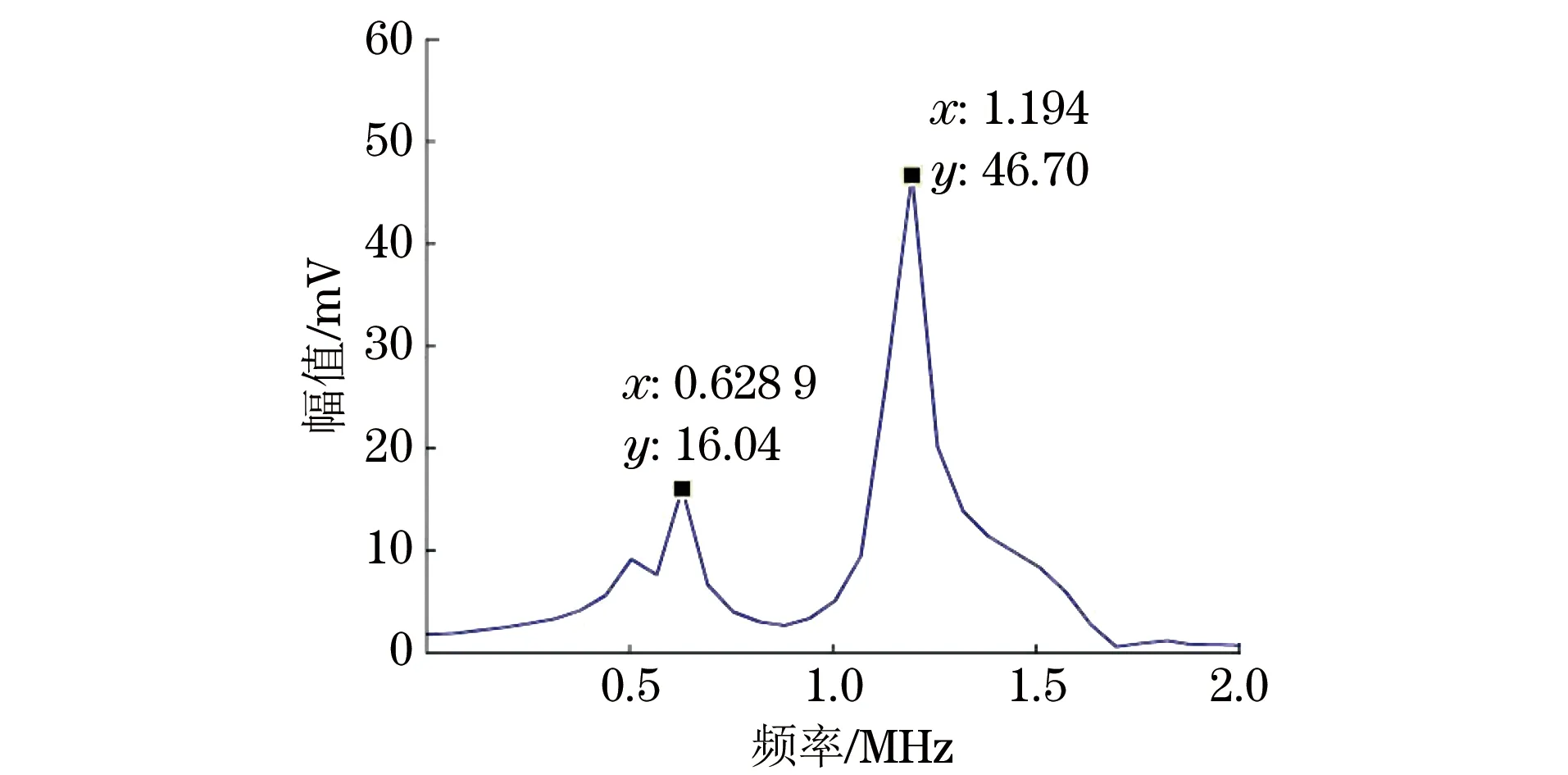
图7 平行凹槽厚度a1处的频谱分布

图8 平行凹槽厚度b1处的频谱分布

对图4中平行凹槽测试体进行谐振试验，从测试体的背面发射声波，探头从背面正对凹槽最低点厚度a1处(厚度5.0 mm)进行试验，对在平行凹槽厚度a1处发生谐振的接收波形进行FFT变换后得到的频谱分布如图7所示。从图7可以看到频率分别为0.628 9 MHz和1.194 MHz的谐振峰，由谐振基本频率正确地计算出测试体的厚度为4.95 mm。再移动探头来测量凹槽最高点的厚度b1(厚度5.5 mm)，对凹槽厚度b1处发生谐振的接收波形进行FFT变换后得到的频谱分布如图8所示，从图8可以看到频率分别为0.570 3 MHz和1.14 MHz的谐振峰，根据谐振频率计算出对应的厚度为5.46 mm，分别正确地检测出了图4中的厚度a1和b1。

3.3 对三角形凹槽测厚

对三角形凹槽进行谐振试验,超声波的发射也是从测试体的背面进行的。对三角形凹槽最低点厚度a2(厚度5.0 mm)处进行试验，并对发生谐振的接收波形进行FFT变换得到的频谱如图9所示，从图中可以明显看到频率分别为0.635 MHz和1.263 MHz的谐振峰。根据谐振频率计算出对应的厚度为4.90 mm，误差为0.1 mm。然后再次改变探头的位置，对凹槽的最高点厚度b2处(厚度5.5 mm)进行试验，对发生谐振的接收波形进行FFT变换得到的频谱如图10所示。从图10中可以看到频率分别为0.570 9 MHz和1.14 MHz的谐振峰，根据谐振频率计算出对应的厚度为5.45 mm，误差为0.05 mm。

图9 三角形沟槽厚度a2处的频谱分布

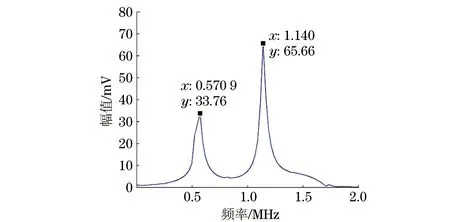
图10 三角形沟槽厚度b2处的频谱分布

3.4 对圆形凹槽测厚

对圆形凹槽进行谐振测厚试验。从测试体的背面发射超声波对圆形凹槽最低点厚度a3处(厚度5.0 mm)进行试验，并对发生谐振的接收波形进行FFT变换得到的频谱分布如图11所示，从中可以得到频率为0.636 4 MHz和1.27 MHz的谐振峰。根据谐振频率计算出对应的厚度为4.89 mm，误差在0.2 mm以内。再次改变探头的位置，在正对凹槽的最高点厚度b3处(厚度5.5 mm)进行试验，对发生谐振的接收波形进行FFT变换，得到的频谱分布如图12所示，从图中可以看到频率分别为0.563 2 MHz和1.151 MHz的谐振峰，根据谐振频率计算出对应的厚度为5.53 mm，误差在0.1 mm以内。

图11 圆形沟槽厚度a3处的频谱分布

图12 圆形沟槽厚度b3处的谐振频率

3.5 技术应用

从试验结果来看，如果在测试体上出现了厚度的减薄，就会存在与底面平行的地方，声波就会在此处发生多次反射叠加产生谐振。此次试验是在已知厚度为5.5 mm和5.0 mm的情况下，检测出其对应谐振频率的。但是在实际的厚度减薄中，由于减薄部分的厚度并不一定是恒定的，所以会检测出多个频率。当测试体存在如图13所示的复杂形状时，会检测到不同厚度与各底面的平行部分厚度相对应的谐振频率。在试验中，检测出厚度最薄的位置才是最安全的。由于厚度薄的测试体的谐振频率高，因此如果在厚度减少部分观测到多个谐振频率，判断出哪个位置对应的一阶基本谐振频率最大，就能判断哪个位置是厚度最薄的部分。

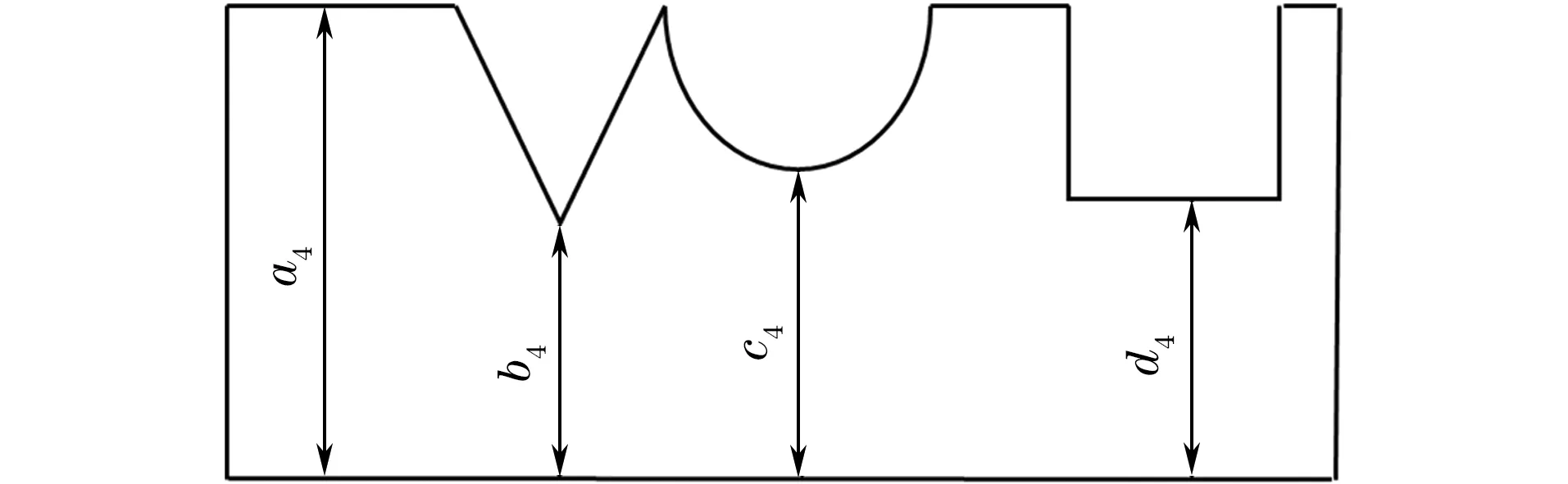
图13 复杂形状测试体的结构示意

4 结语

使用非接触式空气耦合超声谐振法测量技术对测试体进行了厚度测量，对产生的谐振信号进行了傅里叶变换，检出了与测试体厚度相对应的一阶与二阶谐振频率。改变探头与测试体之间的位置，谐振信号的状态也发生变化，厚度越薄处对应的谐振频率越大。用谐振法分别对平行凹槽、三角形凹槽和圆形凹槽测试体的厚度进行了检测，如果有与底面平行的部分，就会在此处检测到谐振信号，检测出与各种厚度相对应的谐振频率，最后计算出各种厚度。