基于小波分析的磁通门信号数字处理方法*
2019-05-28朱豪坤陈国光闫小龙杨智杰
朱豪坤,陈国光,闫小龙,杨智杰
(1 中北大学机电工程学院,太原 030051;2 晋西工业集团有限责任公司,太原 030024)
0 引言
磁通门传感器是一种灵敏度高、稳定性好、测量范围大的弱磁场测量传感器,广泛应用于航空、航天、航海、地质勘探等领域[1-2]。在实际应用中由于磁通门探头的电磁和形状尺寸参数不可能完全对称等因素,导致磁通门信号中存在各种噪声。现有去噪方法是采用波形“门”结合带通滤波的方法降噪[3]。但这种方法在去噪的同时也去除了较多真实信号,降低了信噪比。
小波分析在时、频两域都可以较好的表征信号的局部特点,被广泛应用于各个领域。文中提出了一种小波分析的双芯磁通门信号数字信号处理方法,采用阈值降噪法去除系统中的噪声。通过Simulink建立双芯磁通门系统数字信号处理仿真模型,仿真结果表明该方法达到了良好的去噪效果。
1 磁通门原理及数字处理系统分析
1.1 磁通门原理
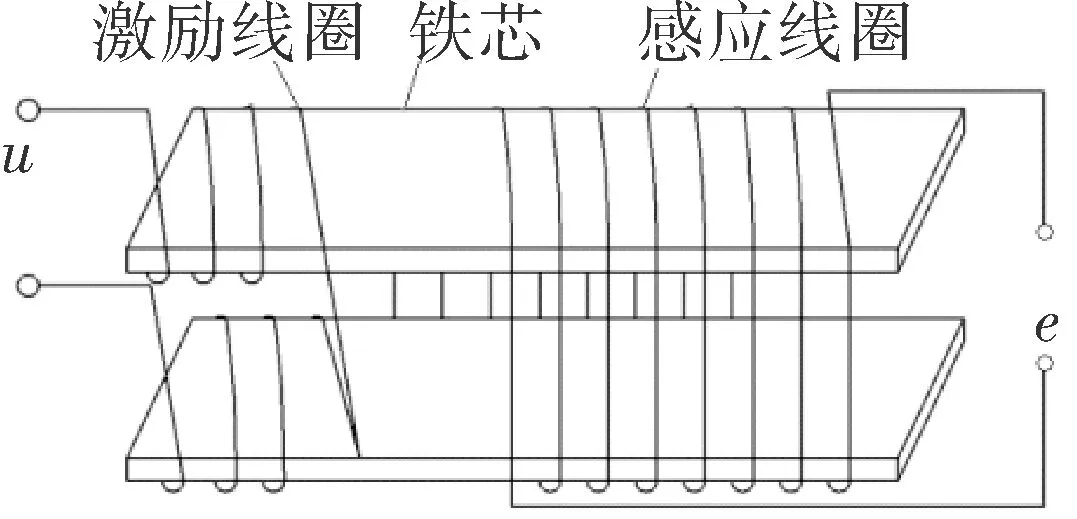
图1 双铁芯磁通门结构图
如图1所示,双芯磁通门探头采用双铁芯结构,由铁芯、激励线圈和感应线圈组成,其激励线圈反向串联。磁通门探头是一种变压式器件,基本原理服从法拉第电磁感应定律[4]。
若将输入频率为f1的正弦激励电压施加于激励线圈上,在铁芯中将产生磁场强度为H1=Hmcos(2πf1t)的激励磁场,且在任一时刻两铁芯中激励磁场的方向都是反向的。被测磁场强度为H0,所以双铁芯磁通门上下铁芯中的磁场强度为:
(1)
铁芯工作在过饱和状态时,使铁芯磁导率μ随激励磁场强度的变化产生周期性的变化,但铁芯磁导率恒为正,说明铁芯磁导率μ为偶函数。同时被测磁场H0远小于铁芯饱和磁场强度Hs和激励磁场强度幅值Hm,所以可以不考虑其对磁导率的影响。将磁导率μ(t)展开为傅立叶级数:
(2)
根据磁感应强度B与磁导率μ和线圈内磁场强度的关系B=μH,可得上下铁芯中产生的磁感应强度BU、BD,则感应线圈内产生的总的磁感应强度为:
B=BU+BD=2H0μ(t)
(3)
从式(3)可以看出激励磁场在感应线圈内产生的感应电势相互抵消,被测磁场在感应线圈中产生的感应电势相互叠加。根据法拉第电磁感应定律,磁通门测得的感应电动势为:
(4)
由式(4)可知,磁通门输出电动势信号只存在偶次谐波[1,5],且磁通门信号脉冲幅值与被测磁场强度成正比。这种通过直接测量感应电压峰值的方法充分利用了磁通门信号的整个频谱,称为脉冲幅值法。
1.2 磁通门信号数字处理系统
如图2所示,磁通门信号数字处理系统的主要环节有:16位A/D转换、16位D/A转换、激励信号、检波信号、功率放大、小波分析、幅值检波、相敏检波。磁通门信号经上述步骤处理后,通过串口通信输出。
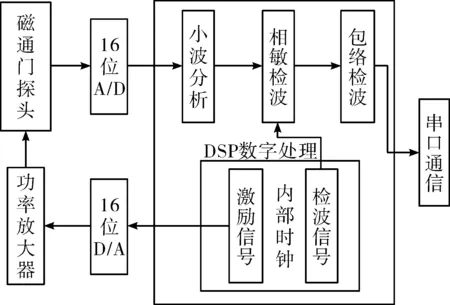
图2 小波处理磁通门信号系统原理图
2 小波分析原理
针对磁通门信号处理的实时性和快速性要求,用Mallat快速算法对磁通门信号进行多分辨率的分解与重构,设母波为ψ(t),φ(t)为其尺度函数,将母波经一系列伸缩与平移,并进行离散得到离散小波[6-7]:
(5)
则{ψj,k(t)}j,k∈Z为正交小波基。Wj=span{ψj,k(t)}j,k∈Z为小波子空间,设通过A/D转换后的信号为e(tn),对于信号e(tn)∈L2(R),V0为L2(R)的一个尺度子空间,则V0可分解为V0=W1⊕W2⊕…⊕Wj⊕Vj,若e(tn)∈V0,则e(tn)的分解公式为:
(6)
式中:cj,k=
(7)
递推算法的示意图如图3所示。
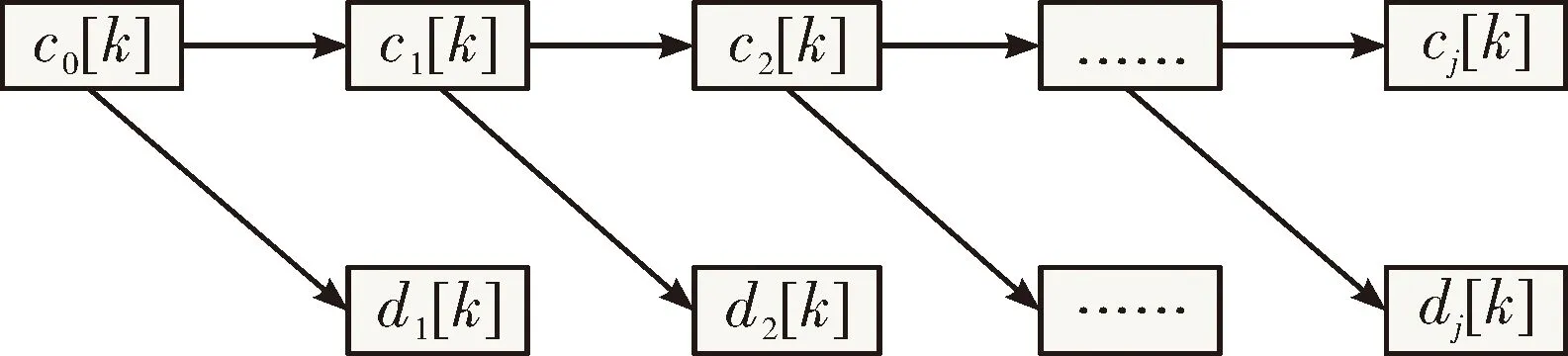
图3 Mallat快速分解算法示意图
将每一层的高频系数选择对应的阈值进行去噪处理,常用的阈值去噪法有硬阈值去噪和软阈值去噪[8-9]。对比两种阈值去噪方法,软阈值去噪较硬阈值去噪有去噪信号信噪比高、信号不失真等特点,因此采用软阈值去噪,软阈值的表达式如式(8)所示。设经过软阈值降噪后的小波系数为d′1,k,d′2,k,…,d′j,k,根据图4 Mallat快速重构算法示意图,可由cj,k和小波系数d′j,k,…,d′2,k,d′1,k,逐级推导出尺度系数为c′j-1,k,…,c′1,k,c′0,k,推导公式如式(9)所示。
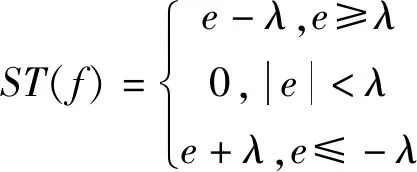
(8)
(9)
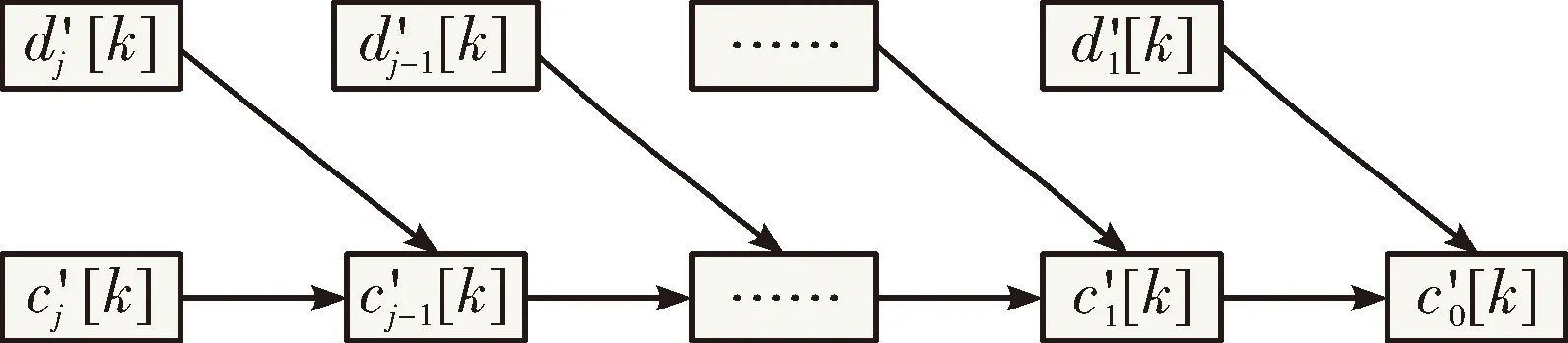
图4 Mallat快速重构算法示意图
经重构得到的信号e1(tn)为:
(10)
3 信号的产生与去噪后处理
通过DSP内部时钟和定时器分频产生频率f1=4 kHz的正弦信号作为激励信号,产生频率f2=8 kHz、电压幅值为1 V的正弦波信号作为检波信号。为使磁通门探头得到较强的磁通门信号,激励磁场的强度幅值Hm需远大于铁芯饱和磁场强度Hs,所以将DSP产生的激励信号通过功率放大器放大,放大后的激励信号电压幅值Vm=12 V。
磁通门信号通过小波降噪后,需要进行处理才能得到相应的方向信息和幅值信息,其后处理工作主要包括数字相敏检波、幅值检波。通过数字相敏检波得到磁通门信号的矢量方向,通过幅值检波得到磁通门信号的峰值。
DSP产生的频率f2=8 kHz的信号与磁通门信号有一定的相位偏差,因为此偏差为定值,所以可以通过试验进行相位校准。设相位校准后的检波信号为s(t),用检波信号对信号e1(tn)进行相敏检波,则被测磁场的方向可由式(11)表征。若D(tn)>0,则被测磁场的方向为正;若D(tn)<0,则被测磁场的方向为负。
D(tn)=e1(tn)·s(tn)
(11)
AD采样频率为f3=1.2 MHz,则一个磁通门信号周期内采样得到150个数据,对一个周期内的数据取其最大值作为这一周期内的输出,充分利用了该周期内的各次谐波信号来反应磁通门原信号。
e2(th+i)=max(e1(th+0),e1(th+1),…,e1(th+150))
(12)
4 仿真处理及分析
使用MATLAB中的Simulink模块对上述磁通门模型及数字信号处理方法进行建模仿真,磁通门相关参数为:激励线圈匝数W1=80,感应线圈匝数W2=120,感应线圈横截面积S=4×10-7m2。
4.1 小波的选择
使用不同小波进行去噪的效果是不同的,在小波去噪的过程中要选出分解后信号与噪声容易分离的小波进行去噪。
在磁场强度为42 155 nT时,通过选用多种小波对磁通门信号进行去噪分析,选取了其中两种小波在相同分解层数(2层分解)下进行去噪对比,图5(a)为采用coif1小波进行分析去噪后的信号,可以看出去噪后信号中依然含有部分噪声,说明使用此小波难以使原信号和噪声信号较好的分离;图5(b)为采用haar小波进行分析去噪后的信号,可以看出使用此小波去噪后的信号中基本不夹杂明显噪声,信噪比较采用coif1小波去噪高,说明此小波能有效的从含噪信号中区分源信号和噪声。根据对多种小波进行试验对比,本系统采用haar小波对磁通门信号进行降噪。
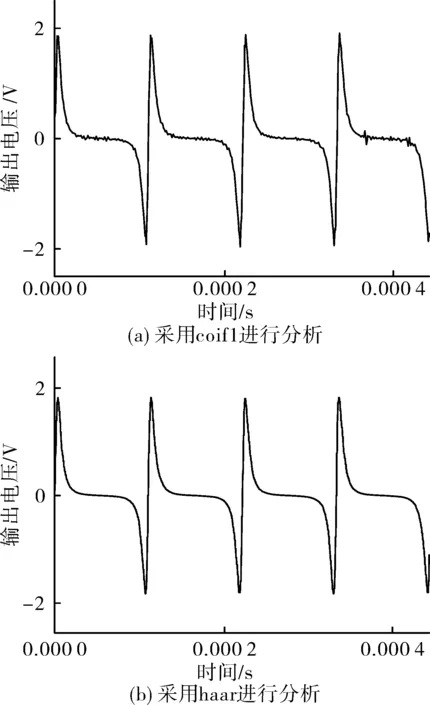
图5 不同小波去噪后信号对比
4.2 小波参数的选定
使用同一小波对信号采用不同分解层数、不同阈值去噪取得的效果是不同的,这需要通过多次试验进行分析对比,取得较优效果的小波分解层数和去噪阈值。
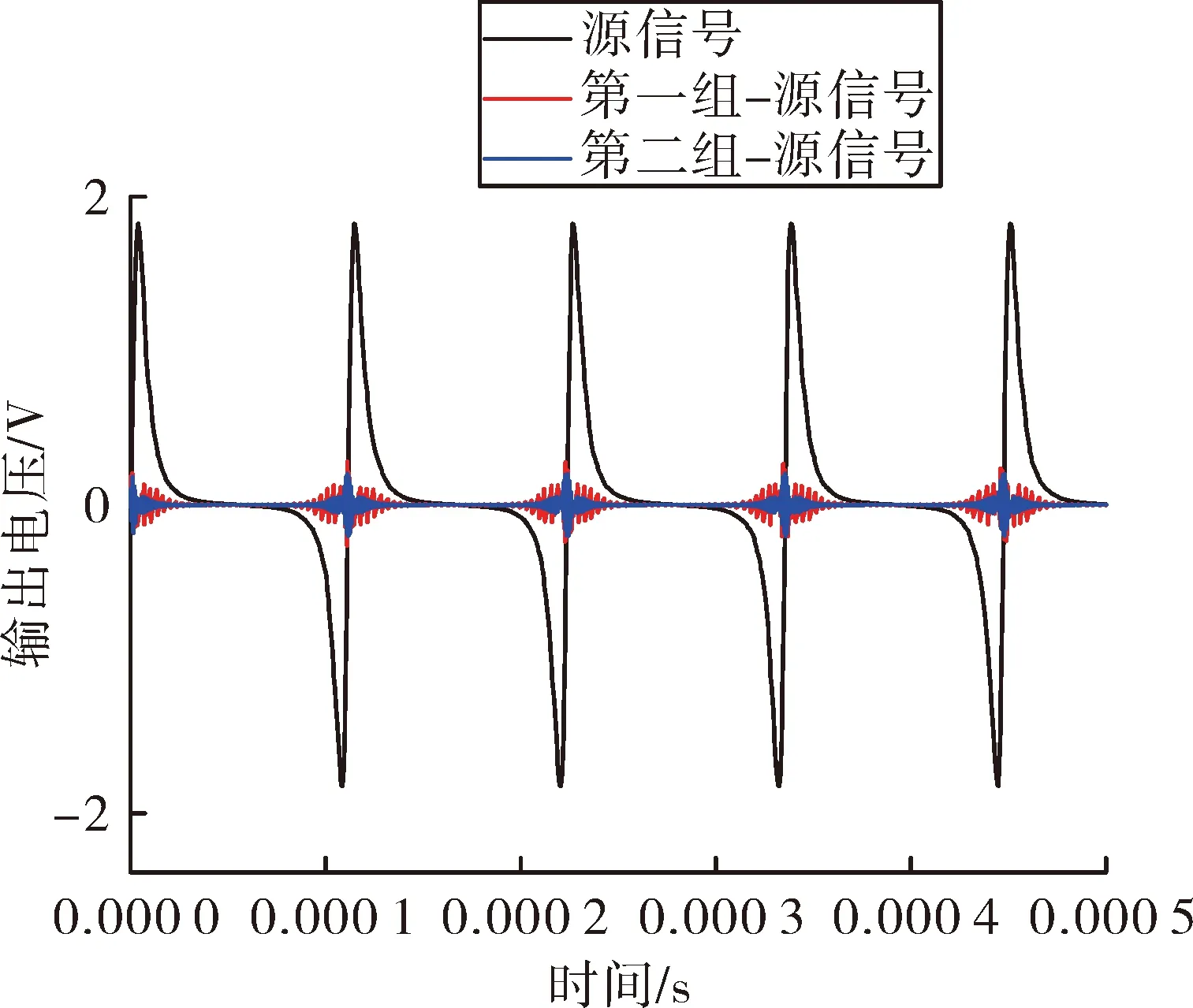
图6 不同层数、阈值去噪后信号与源信号的误差
在使用haar小波作为母波,通过选择不同分解层数和不同去噪阈值对信号进行多次去噪试验,选定了两组较优分解层数进行分析对比。第一组是进行3层小波分解、去噪与重构,第二组是进行2层小波分解、去噪与重构,两组数据去噪后信号与源信号的差如图6所示。从图中可以看出,使用第二组数据去噪后的信号与源信号的误差较小,说明采用第二组数据去噪效果更好,且第二组分解层数比第三组更少,进行小波分解、去噪、重构的速率更快。所以经对多次试验对比,采用2层小波分析的haar小波进行去噪。
4.3 去噪效果
取环境磁场H0=42 155 nT,根据上述所选定小波及软阈值参数,利用文中所建磁通门数字信号处理仿真模型对其进行仿真,得到经小波处理前后的磁通门信号如图7所示。
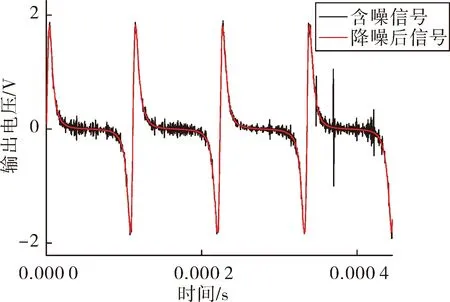
图7 42 155 nT时磁通门信号小波降噪前后对比
4.4 试验结果
取环境磁场H0∈(-60 000 nT,60 000 nT),用所建Simulink磁通门仿真模型,仿真间隔ΔH=10 000 nT进行仿真,仿真结果如图8所示。从图中可以看出,被测地磁场大小与磁通门信号幅值线性相关,模型实现了对磁场方向的检测,并且具有较好的磁场测量范围。
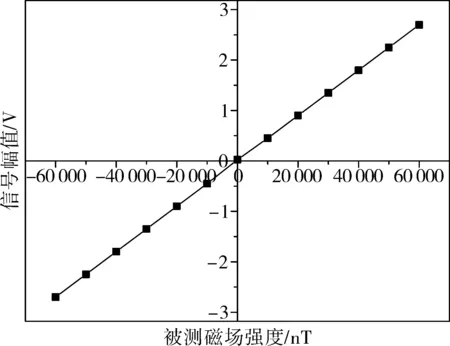
图8 磁通门信号幅值随磁场变化
取环境磁场H0∈(42 155 nT,42 205 nT),仿真间隔ΔH=1 nT进行仿真,仿真结果如图9所示,从图中可以看出,该系统的测量精度为3 nT。数据拟合出来的线性表达式如式(13)所示:
V=0.000 039 8H0+0.021 3
(13)
拟合优度R2=0.988 6,测量范围内的数据线性关系良好。
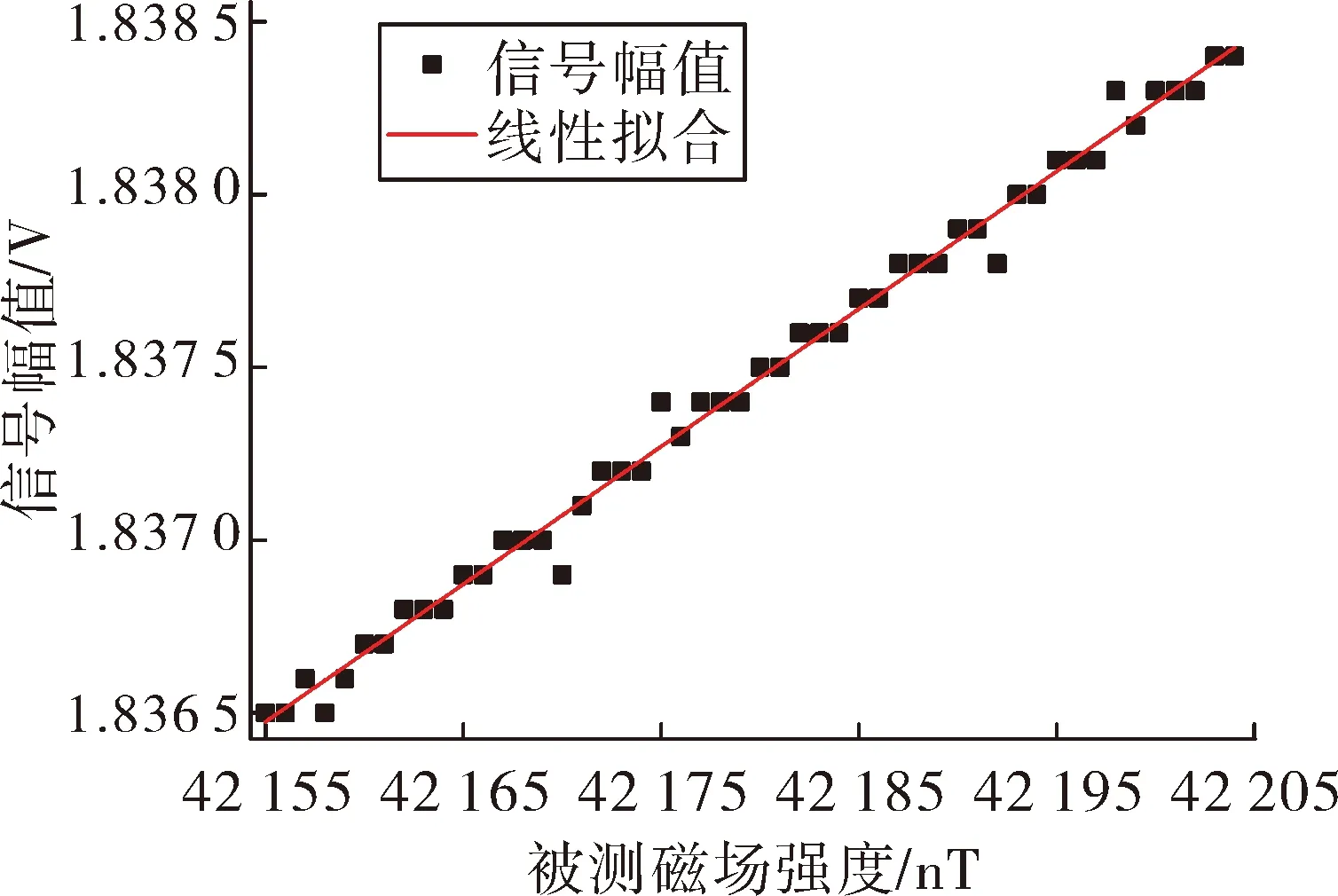
图9 H0∈(42 155 nT,42 205 nT)对应信号与拟合直线图
5 结论
通过建立基于小波去噪的双芯磁通门数字信号处理系统,优化了现有磁通门数字信号处理方法存在的相关问题,提高了去噪后磁通门信号的信噪比,从而提升了磁通门传感器的测量精度。通过simulink建立该系统的仿真模型,仿真结果表明:该系统可实现对磁场方向的检测,系统所得磁通门信号幅值与被测磁场有良好的线性关系,磁通门传感器测量精度达到3nT,较现有方法有所改善。验证了小波去噪应用于磁通门信号数字处理的可行性,为磁通门传感器提供了一种新的数字信号处理方法。
