反超低空突防的全程弹道设计优化研究*

马新鹏，李旭昌，吴达，陈 峰

(空军工程大学防空反导学院，西安 710051)

0 引言

防空导弹在拦截超低空目标时，由于受到地形或者地海杂波的影响，会受到镜面反射信号的影响，从而形成多路径效应问题[1-2]，导致雷达导引头无法有效地跟踪识别目标，严重影响导弹的作战性能。随着超低空飞行技术的快速发展，研究具有反超低空突防能力的防空导弹就显得尤为重要。

导弹和镜像目标的连线与水平面的夹角称为擦地角[3]。研究指出：当擦地角达到某个角度时，地海杂波反射系数最小，此角度称为布儒斯特角[4-5]。因此，采用垂直极化的雷达照射信号，通过弹道设计和导引律优化，使导弹攻击目标过程中，擦地角接近布鲁斯特角，可以减弱地面镜像干扰的影响，是拦截超低空目标可行的技术途径。文中就是基于这种思想，设计了一种初段(程序转弯)+中段(导引律补偿)+末端(比例导引律)的总体弹道方案，进行Matlab仿真验证分析，并在此基础上进行弹道优化，分析不同参数对导弹弹道特性的影响。

1 多路径效应描述与超低空拦截模型

1.1 多路径效应问题描述

如图1所示，F为地海杂波反射点，β为擦地角，目标信号返回路径为P1，地海杂波反射回的路径为P2。目标超低空飞行时的地海杂波反射强度大(有时甚至超过目标本体),因此导引头可能会将镜像目标T′当作目标进行攻击。

地海杂波的反射系数随擦地角的变化而变化，当擦地角达到某一个值时，反射系数最小，此反射系数最小时对应的擦地角称为布儒斯特角。在不同的环境下(草地、海面)，布儒斯特角的大小也不尽不同。以某一恒定环境为例[6]，其反射系数随擦地角的变化规律如图2。

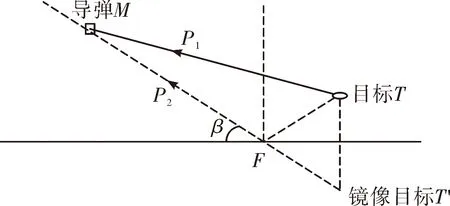
图1 导弹、目标及镜像几何关系

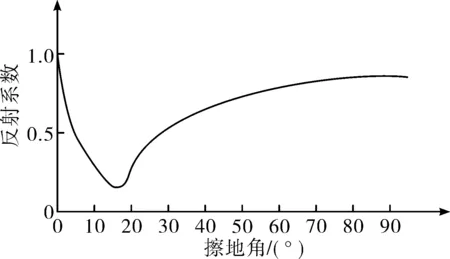
图2 反射系数与擦地角关系

1.2 擦地角的近似计算

从拦截超低空目标的需求出发，要保证中段擦地角约束在布儒斯特角附近。但在实际飞行中，导弹难以实时测量擦地角的大小，并且从导引律的角度来看，通过导弹和目标的视线角更易实现，因此要首先分析弹目视线角与擦地角的差异[7]。

以飞行高度150 m为例，分别计算不同距离下的擦地角均为10°时的弹目视线角数值。

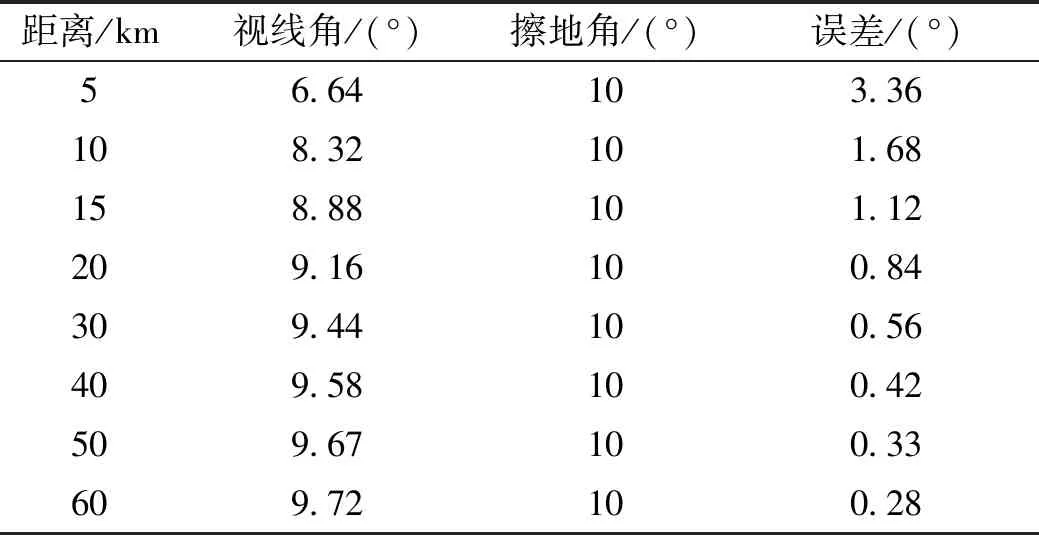
表1 擦地角与视线角的误差

从表1可以看出，拦截超低空目标的飞行弹道，当弹目距离较远时，真实目标和镜像目标相对于导弹的视线角差异较小；接近目标时，两者之间的差异增大。虽然两个角度之间有一定的误差，但是在导引律的设计过程中，针对视线角进行修正更容易实施，因此考虑设计中段制导律时弹目距离较远，可针对视线角或视线角速率进行修正，将其约束在布儒斯特角附近，提高导弹制导精度。

1.3 超低空拦截模型

下面进行超低空拦截模型的建立。三维空间可为纵向的俯仰平面和横向的转弯平面，为方便分析只研究纵向的俯仰平面即可，如图3所示：M代表导弹，vm为导弹的速度，θm为导弹弹道倾角，am为导弹的法向加速度；T代表目标，vt为目标的速度，θt为目标的航迹倾角，at为目标的法向加速度；R为导弹到目标的距离；q为导弹和目标之间的视线角；按照导弹飞行力学[6]，所有角度沿逆时针旋转为正，顺时针为负。

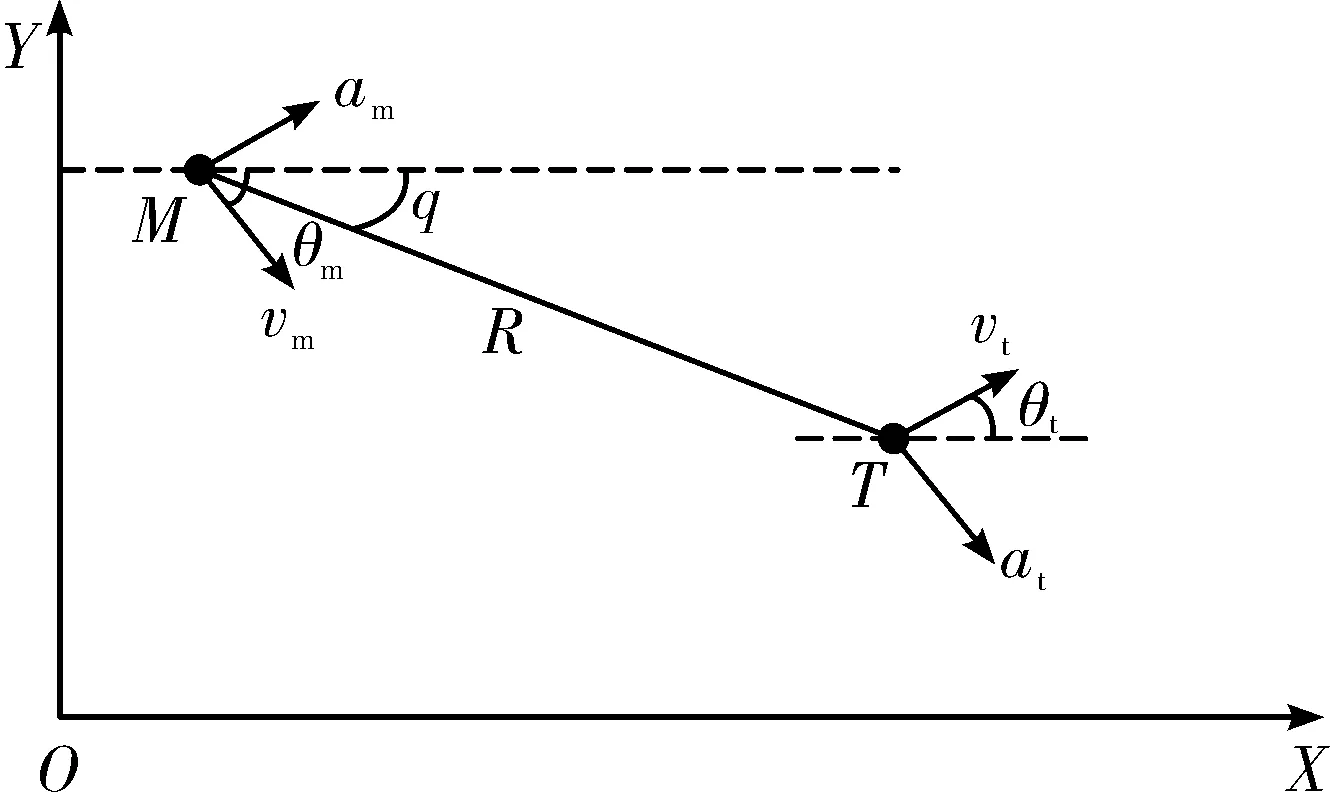
图3 弹目相对运动关系

由图3可知，弹目间的相对运动方程[7]为：

(1)

根据式(1)可得出：

(2)

2 弹道设计

导弹在拦截目标的过程中，目标紧贴于地面或者水面飞行，导弹可在较高的高度飞行，通过雷达导引头下视跟踪目标。目标运动的特点决定了对于超低空目标拦截的弹道形式。

导弹从地面垂直发射，到达一定高度后向目标来袭方向转弯，导引头截获目标后进入中制导段，中段飞行时通过弹上雷达导引头探测目标信息，末段进行俯冲攻击。在转弯后中段飞行的过程中，需要将视线角控制在布儒斯特角附近。

按照以上的需求，弹道设计方案如图4所示。

图4 弹道方案

根据飞行弹道的特点，可将其分为初始转弯段、中制导段和末端攻击段[8]。

2.1 初始转弯段

对于拦截超低空目标的飞行弹道设计而言，初始转弯段采用程序控制，与目标无关。导弹以预定的仰角发射后，到达一定高度后向来袭目标方面转弯飞行。此过程中，通过合理参数设置，采用给定弹道倾角的设计规律，为中段的导引飞行提供较好的初始条件。具体分为以下几个阶段：

1)助推段

导弹发射后，在助推器的作用下，按照给定的弹道倾角(弹道倾角为常值)加速爬升。记助推器工作时间为t1，则弹道倾角和加速度变化规律为：

(3)

2)滑翔段

助推器工作结束后，导弹保持速度不变，接着向上爬升，上升到一定高度开始向目标转弯。记开始转弯时间为t2，则弹道倾角和加速度变化规律为：

(4)

3)转弯段

滑翔段结束后，导弹开始按照预定程序开始转弯，并最终转平。转弯段弹道倾角的变化规律可按飞行时间给出。记转弯段结束时间为t3，为满足飞行过程中弹道倾角和弹道倾角变化率连续，转弯段弹道倾角变化规律需满足以下条件：

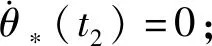
2.2 中段制导段

现役导弹大多采用经典的比例导引律或修正的比例导引律，而导弹按照比例导引法飞行时，视线角基本取决于导弹发射的初始信息，并没有布儒斯特角的约束要求，一般无法满足布儒斯特角约束。因此，可以在现有比例导引律的基础上，通过引入补偿量，对比例导引律进行修正，使导弹攻击过程中视线角满足布儒斯特角约束。修正后的导引关系可写为：

(5)

式中x为补偿量。

基于上述分析，问题即转变为：如何构造补偿量x，在不增加新的反馈信号的前提下，使其按照改进的导引律实现布儒斯特角约束要求[9]。

图5 视线角速度变化曲线

由图5可知，从0时刻到tf时刻，视线角速度的变化规律满足三次样条曲线，其多项式表达式可写为：

(6)

式中：a、b、c、d为待定参数。根据视线角速度变化规律设计要求，上式需要满足的约束条件具体为：

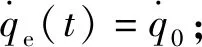
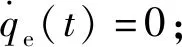
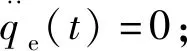
可解得待定参数a、b、c、d，得到视线角速度变化规律前半段。因此，满足布儒斯特角约束要求的视线角变化规律可表示为：

(7)

下面进行中制导律的推导：

根据导弹-目标相对运动方程，在Δt时间内，由补偿量所引起的视线角速度变化量可表示为：

(8)

在导弹攻击目标过程中，雷达导引头和控制系统的工作频率较高，因此可假定在较短时间内，补偿量所引起的导弹弹道倾角变化为小量(即xΔt为小量)，则有：

sin(xΔt)≈xΔt, cos(xΔt)≈1

(9)

则上式可写为：

(10)

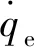
(11)

2.3 末端攻击段

进入末端后，导引头已经可以有效区分目标，因此可以解除布儒斯特角的约束要求，从而利用导弹自身的导引律设计，实现对目标的有效攻击[10]。通常，采用比例导引律为：

(12)

也可根据型号设计，采用扩展比例导引律。

3 弹道仿真

按照上一节所设计的初始转弯段、中段制导段以及末端攻击段的弹道方案，对导弹飞行过程进行仿真分析[11]。

设超低空目标贴着地面做匀速直线飞行，初始高度yt=100 m，初始位置为xt=80 km，速度vt=270 m/s，弹道倾角θm=0°；导弹从地面垂直发射，助推段加速度am1=30g，发动机工作时间t1=6 s，转弯段加速度am2=1g，转弯段开始时间t2=8 s，转弯段结束时间t3=16 s，结束时弹道倾角θm=0°，中段调整时间tf=5 s，转入末端距离X1=6 km；布儒斯特角在15°左右。

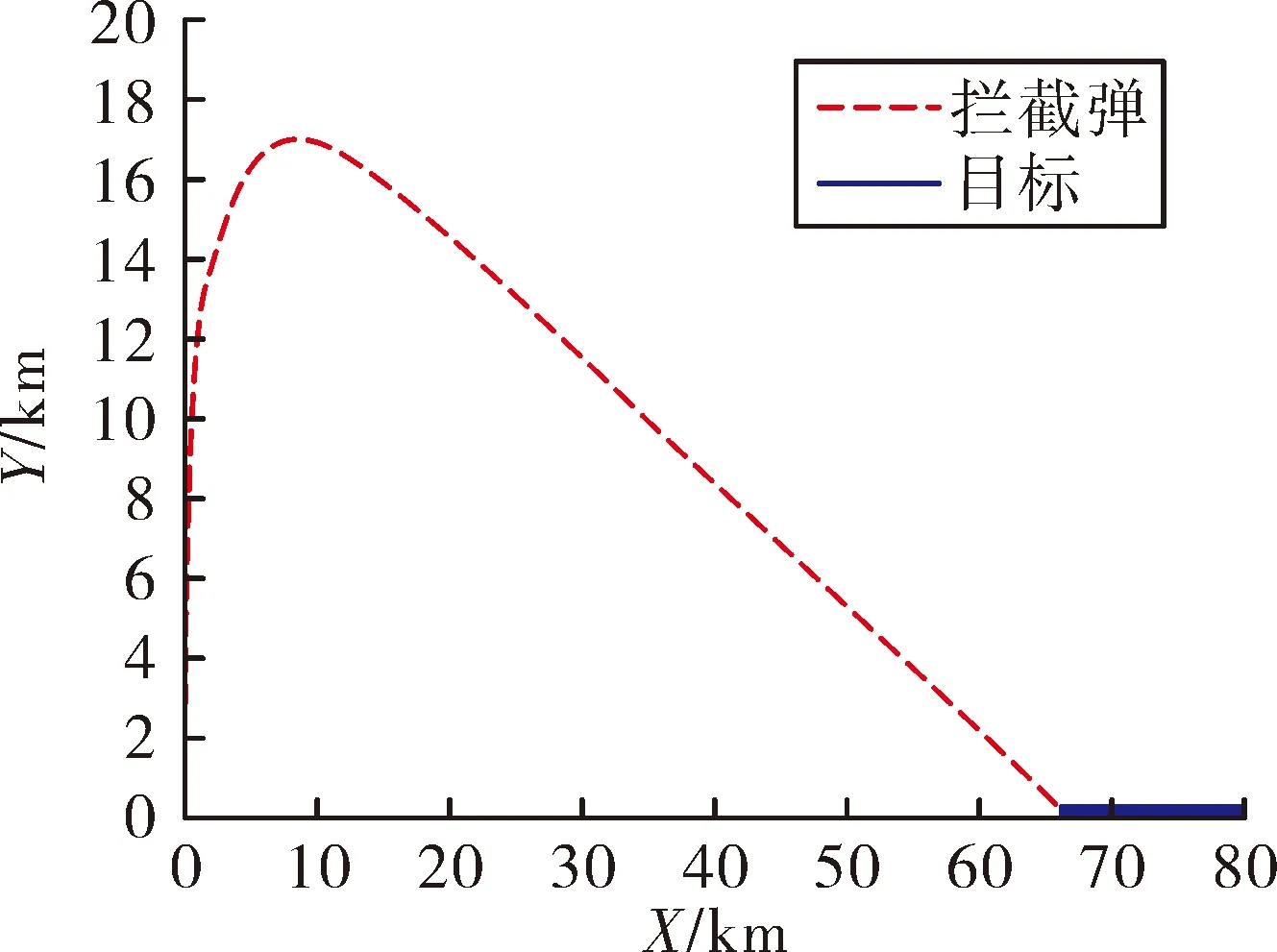
图6 导弹/目标运动轨迹

由图6可以看出，导弹从地面垂直发射，经过初段程序转弯，中段制导，再加上末段打击，最后成功拦截目标，而且所设计的弹道较为平直，大大增强了导弹的机动性，降低了过载，提高了制导的精度。由图7、图8可以看出，在转弯结束后，导弹视线角能够快速向布儒斯特角靠近，并且到达后能够保持不变，视线角速率变化也趋于零，满足制导要求。由图9可以看出，程序转弯结束后导弹的弹道倾角为0°，满足设定值，并且弹道后期速度倾角也基本保持不变。

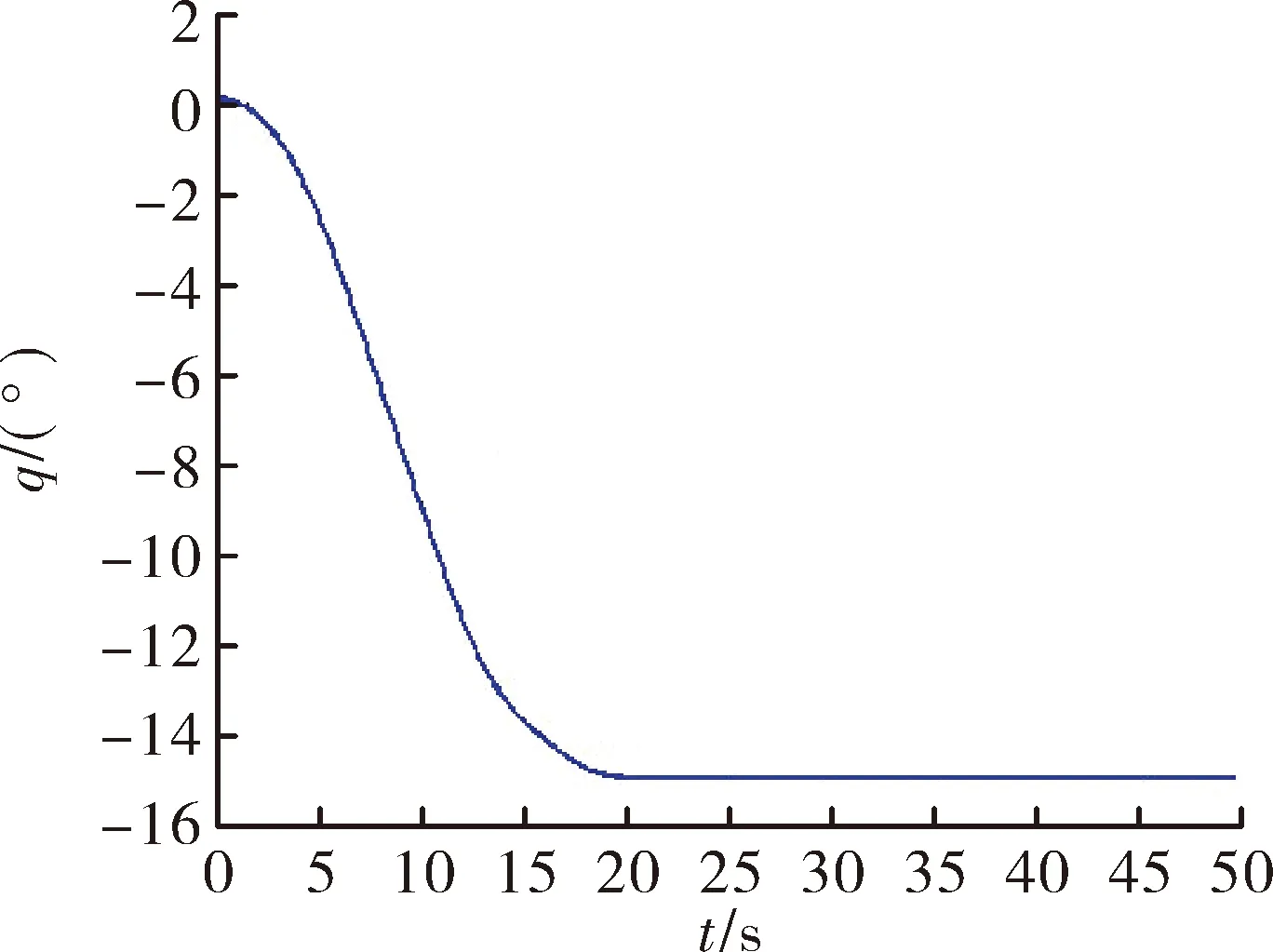
图7 视线角变化图

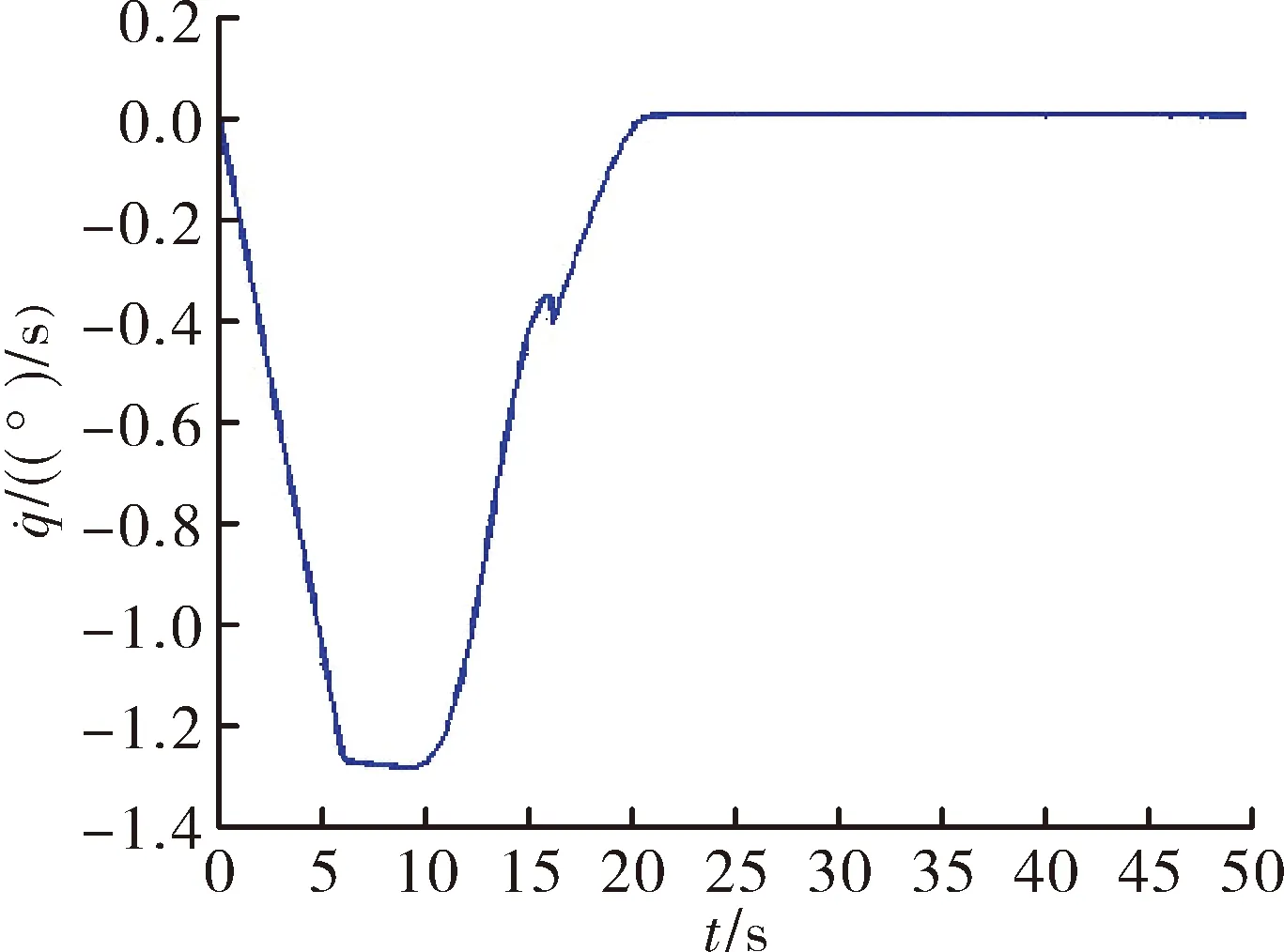
图8 视线角速率变化图

图9 弹道倾角变化图

4 弹道优化

从上节的弹道仿真结果中可以看出，当初段结束后，导弹采用修正的比例导引法，将视线角转动到期望视线角。

但在过渡段飞行过程中，导弹法向过载变化相对剧烈，若参数选取不合理，就会严重影响弹道特性，甚至会出现导弹飞行弹道无法满足布儒斯特角约束，不能按照预定方案攻击命中目标。因此需对弹道各段参数进行优化。为便于研究，约束条件保持不变，分别改变转弯段开始时间t2，转弯段结束时间t3，结束时的弹道倾角θm和中段调整时间tf，对比观察它们对导弹飞行弹道的影响。

1)转弯段开始时间t2

在此参数分析中，转弯段结束时间均为t3=16 s，结束时的弹道倾角均为θm=0°，中段调整时间均为tf=5 s，观察转弯段开始时间t2分别为4 s、6 s、8 s、10 s。

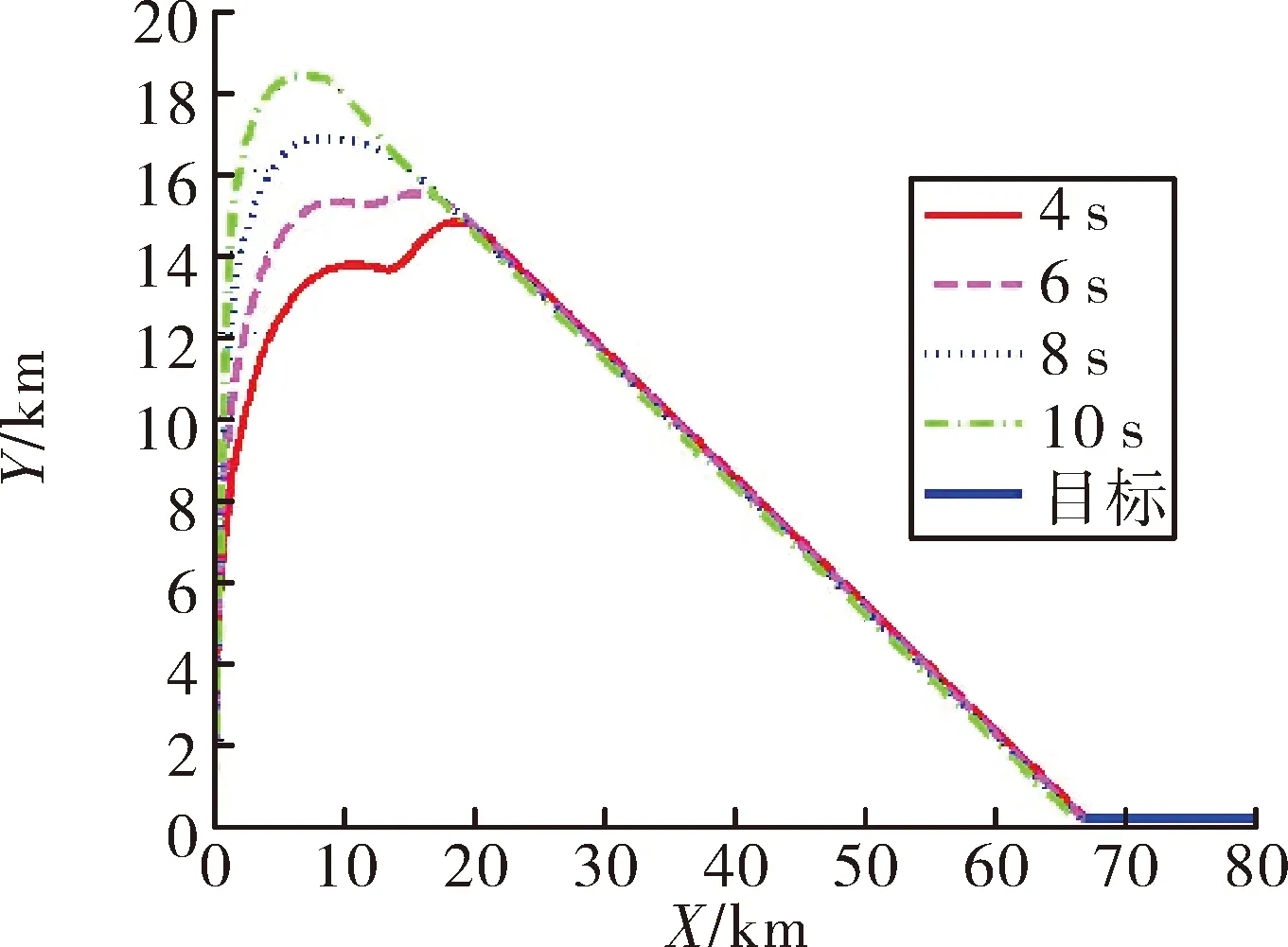
图10 不同t2下的弹道轨迹图

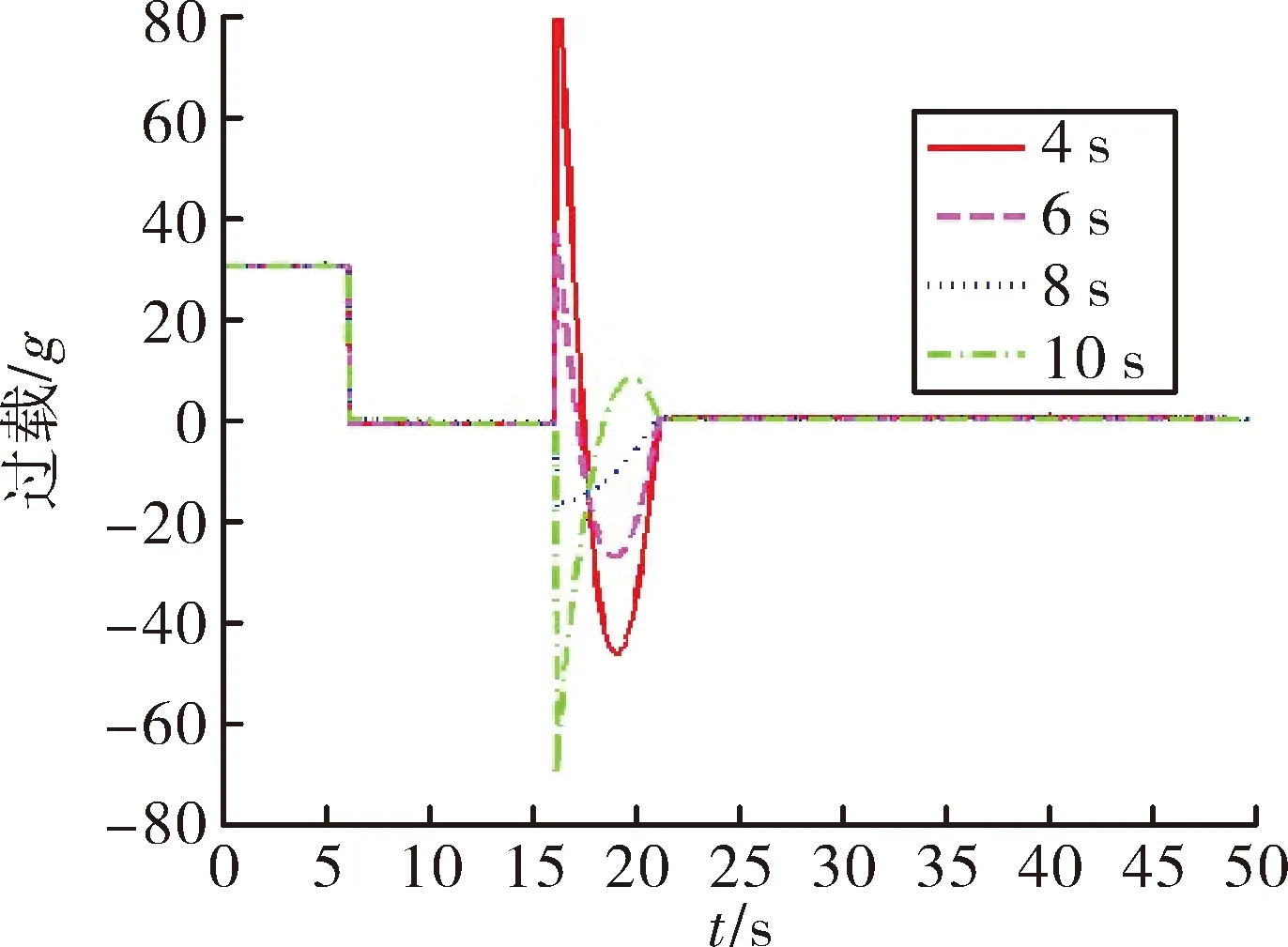
图11 不同t2下的过载变化图

由图10、图11可以看出，转弯越早，导弹达到的最大高度越小，中制导段的初始视线角越小，体现在弹道上，助推转弯结束后，导弹还需要略有爬高，才能调整到布儒斯特角的约束要求；反之，转弯越晚，中制导段的初始弹目视线角越大，为满足约束要求，需要将弹道进行压低。如果参数设计合理，则弹道连续光滑过度，过载较小。

2)转弯段结束时间t3

在此参数分析中，转弯段开始时间均为t2=8 s，结束时的弹道倾角均为θm=0°，中段调整时间均为tf=5 s，观察转弯段结束时间t3分别为15 s、16 s、17 s、18 s。

由图12、图13可以看出，转弯时间对于弹道也有较为明显的影响。转弯持续时间越长，助推段结束时刻的高度就越大，进入中段需要进行弹道压低，从而造成中段的初始过载较大。

3) 转弯结束时的弹道倾角θm

在此参数分析中，转弯段开始时间均为t2=8 s，转弯段结束时间均为t3=16 s，中段调整时间均为tf=5 s，观察转弯段结束时弹道倾角θm分别为4 s、6 s、8 s、10 s。

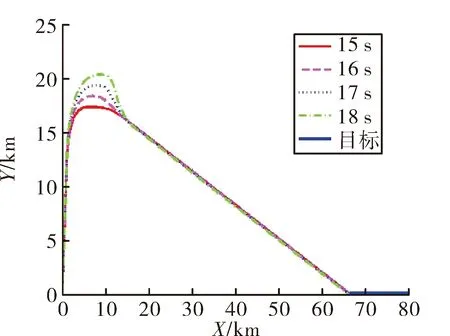
图12 不同t3下的弹道轨迹图

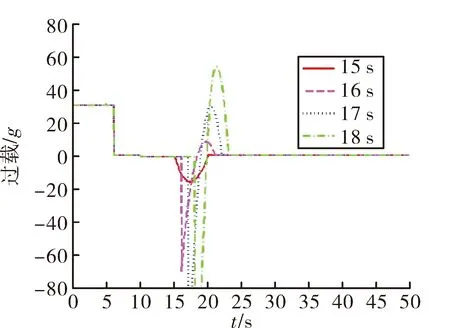
图13 不同t3下的过载变化图

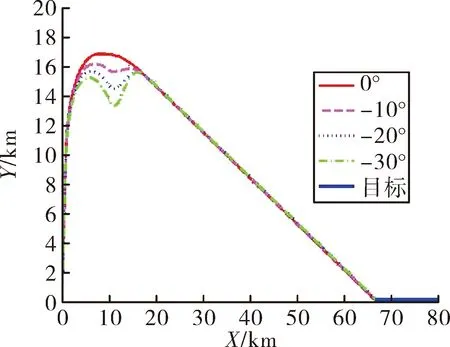
图14 不同θm下的弹道轨迹图

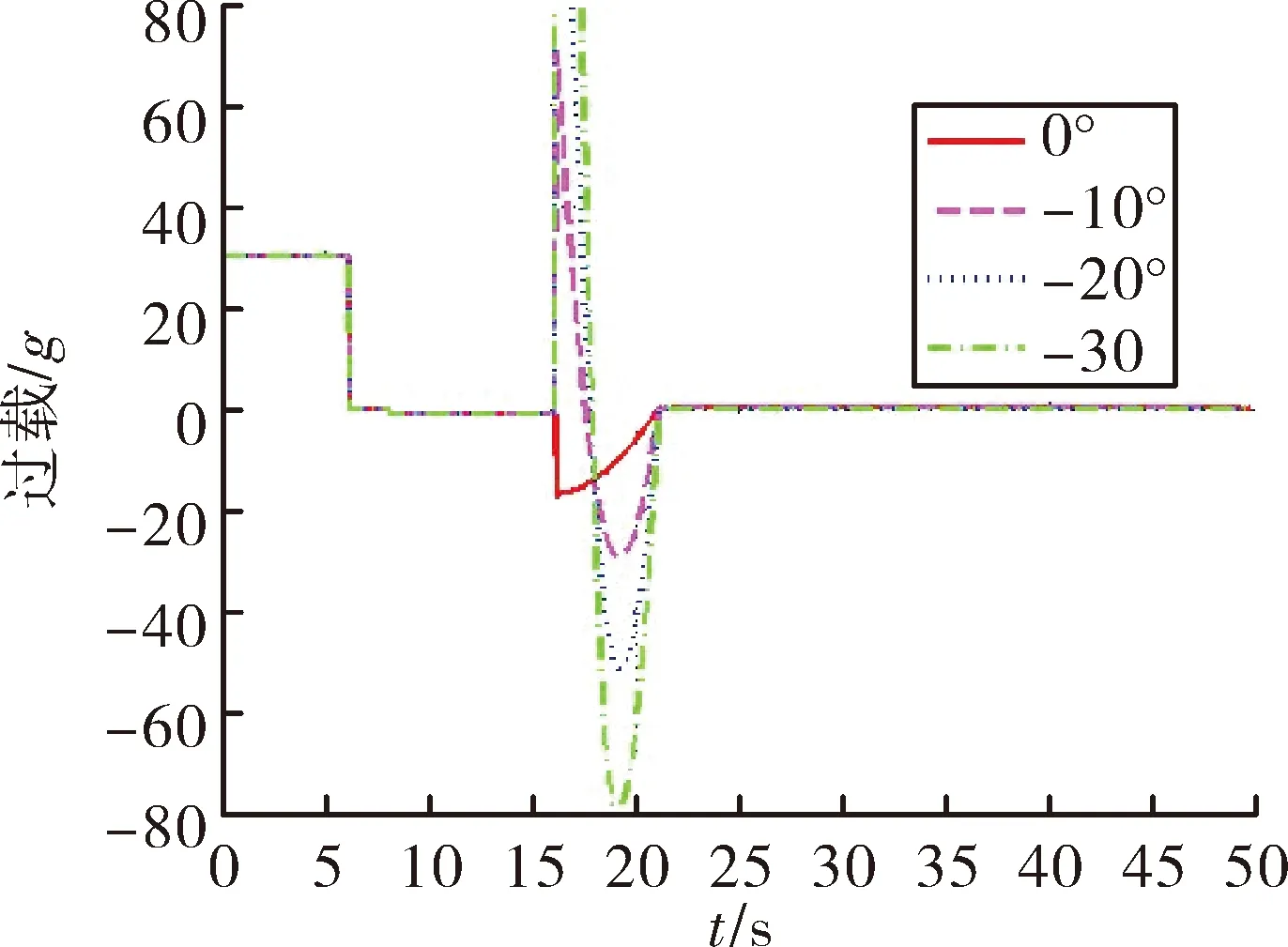
图15 不同θm下的过载变化图

由图14、图15可以看出，转弯结束时刻的弹道倾角不同，一方面导弹高度有所差异，另一方面中制导段的初始条件变化，对于过载有较大的影响。就上述参数而言，弹道倾角越小，更有利于助推转弯段到中制导段的平滑过渡。

4)中段调整时间tf

在此参数分析中，转弯段开始时间均为t2=8 s，转弯段结束时间均为t3=16 s，结束时的弹道倾角均为θm=0°，观察中段调整时间tf分别为4 s、6 s、8 s、10 s。

图16 不同tf下的弹道轨迹图

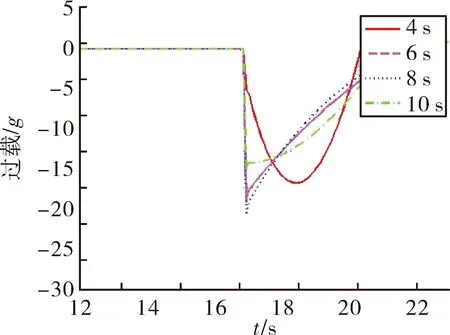
图17 不同tf下的过载变化图

由图16、图17可以看出，相同的助推段条件下，调整时间tf越长，中制导段的过载越小，弹道越平滑。但是，调整时间长，意味着跟踪目标的滞后，这与弹道平滑要求相矛盾，需要综合权衡考虑。

5 结束语

文中讨论了导弹在垂直发射条件下的超低空目标拦截的问题。针对在拦截过程中出现的多路径问题，确定了布儒斯特角的位置，建立拦截弹道模型，研究出将视线角约束在布儒斯特角附近的改进比例制导律，使地海杂波干扰降至最低；将弹道分为初始转弯段、中制导段和末端攻击段，设计出了一种导弹从发射到最后击中目标的全程弹道，并进行了仿真验证。结果表明，所设计的弹道较为平直，并且满足要求，制导精度较高，具有较强的借鉴意义。