载体机动和磁干扰环境下的航姿算法研究

李乃星， 曹培培， 刘圣起， 于 欢

(上海无线电设备研究所，上海201109)

0 引言

基于低成本MEMS(Micro-Electro-Mechanical System)陀螺仪、加速度计以及微磁强计的航姿系统是一种自主式的载体姿态测量系统，具有体积小、功耗低、成本低的优势，广泛应用于小型飞行器、智能机器人以及人体的运动分析。在该类应用中存在载体运动机动性强和运动环境磁干扰较大的情况，低成本的MEMS传感器精度低、漂移大且具有高噪声，在载体运动机动性强时加速度计产生的扰动加速度将会过大，而磁强计易受到环境磁干扰而使其数据精度下降甚至完全不可用，以上问题均将导致姿态信息不可靠[1-3]。

针对以上问题，目前常用的解决方案主要有以下几类：将航姿系统和卫星系统组合使载体保持较高的姿态精度，但这需要额外增加卫星导航模块，且卫星模块在信号遮挡环境中无法工作;而基于卡尔曼滤波及其改进版本的姿态求解方案模型多较为复杂，运算量较大;基于互补滤波器的姿态解算方法实现简单但无法针对小的扰动进行在线的信息补偿，故该算法的精度也会相应下降;梯度下降法求解姿态的方案只有简单的加法和乘法，已被证实是一种高效的姿态求解方案，但该算法无法对传感器数据的误差进行在线补偿，在传感器数据误差较大时姿态解算精度会大幅下降，具有一定的局限性。卡尔曼滤波求解姿态算法可对数据误差进行在线补偿，但其姿态解算模型复杂，运算量大，不易于实现[4-6]。因此，综合各方法特点，设计具有抗机动性扰动功能的新型航姿算法则变得具有一定意义。

1 姿态解算方案

针对上述问题，本课题提出利用自适应卡尔曼滤波对传感器测量值进行预处理，利用梯度下降法完成对处理后测量值的姿态解算与姿态融合的姿态解算方案，使航姿系统具有了抗机动性扰动能力，方案流程图如下所示。

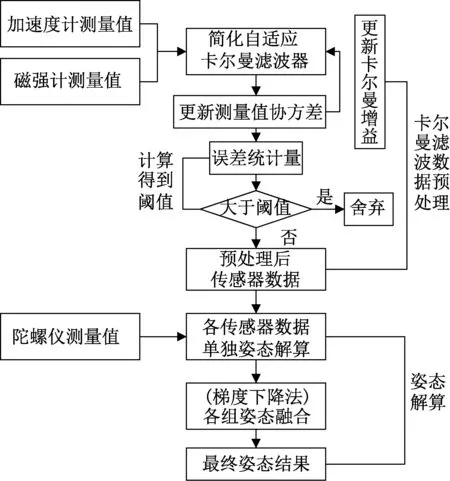
图1 方案总体流程图

A HRS系统的姿态解算过程依赖于加速度计等传感器提供的信息，为提升算法实用性，文章采用只有加法和乘法运算的四元数法进行姿态描述。绕导航坐标系的三个坐标轴x、y、z 轴旋转的三个角分别为横滚角θ，俯仰角γ航向角Ψ。文章采用二阶龙格库塔法利用陀螺提供的角速度数据进行四元数微分运算，计算公式如下所示。

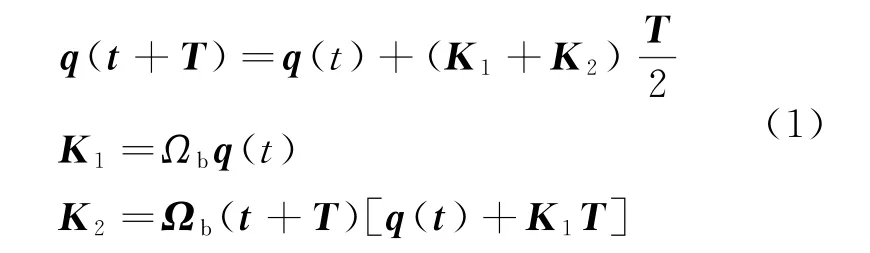
式中：q 为四元数模型;T 是数据更新周期;Ωb为角速度转置矩阵，三轴姿态角可利用上述四元数进行描述，针对四元数进行更新即可完成对姿态角的更新[7]。

综合考虑低成本MEMS 传感器的特性和算法的实用性，文章采用了梯度下降法将陀螺仪、加速度计和磁强计的传感器数据进行融合来提供载体最终的姿态结果，计算公式如下。

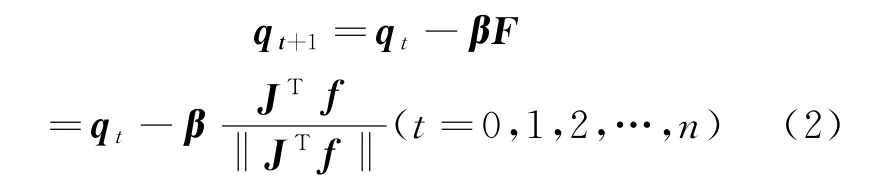
式中：q 为四元数矩阵;β 为在梯度下降方向上更新的步长;f 表示基于不同传感器解算出的姿态角差值;J 为多元向量f 的导数。根据如上所示的梯度下降融合算法，既可以将MEMS陀螺仪、加速度计和磁强计的传感器信息进行融合[8-11]，从而实时的得到更加准确的姿态信息。

2 关键技术实现

2.1 卡尔曼滤波化简

引卡尔曼滤波算法能从随机的干扰当中利用量测值信息估计出所需的最优信息。传统卡尔曼滤波的五个递推公式如下所示。

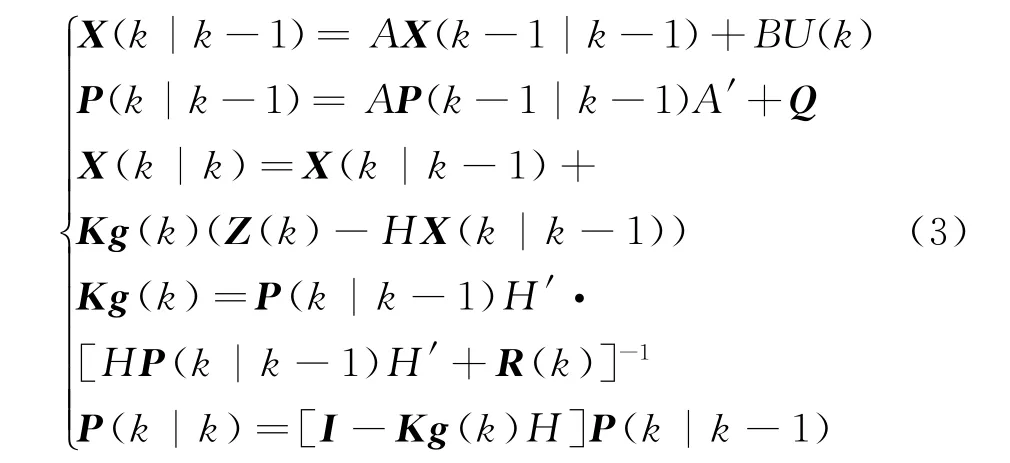
基于此方法的原理，本课题将传统的卡尔曼滤波器模型中的五个基本公式精简为如下所示的四个公式。

式中：P 为状态量的协方差矩阵;Q 为状态转移协方差矩阵;即观测量协方差矩阵;R 为测量值噪声协方差矩阵;Kg 为卡尔曼滤波增益;I 为单位矩阵;X 为滤波的输入和输出量;Z 为实际测量值。

由于滤波的状态量与观测量均为加速度和磁强数据，传统卡尔曼模型中的系数矩阵A 设置为单位阵，系数矩阵B 设置为零矩阵，则滤波的状态一步预测过程等式两侧相等，即可省略。故滤波更新过程可直接先对协方差P(k|k-1)进行更新，矩阵Q 为白噪声。利用上述公式的关系即可实现对协方差P 和卡尔曼增益Kg 的更新，同时，本课题将观测量的更新过程与估计值的导入过程合为一步，得到数据最终估计值X(k)[12]。

文章提出的简化滤波器模型在不降低运算精度的前提下，精简了运算步骤。且该模型中应用的矩阵均为对角矩阵，一定程度上减小了滤波过程的运算量，提升了文章提出的姿态解算方案的实用性。

2.2 传感器误差补偿

上述公式中R(k)为加速度和磁强实测数据对应的协方差的值，该值随实测数据的变化而变化，文章根据两种传感器输出的数据特点，定义了R(k)的更新方式，根据其特点提出了针对两种传感器输出数据统计量，并根据该统计量对传感器输出的数据进行筛选，从而去除因机动性扰动而产生的误差过大的传感器输出的数据，提升了航姿系统的机动性与抗磁干扰能力。

2.2.1 加速度误差协方差

根据MEMS加速度计输出数据的特点，可以将加速度输出模型简化如下。

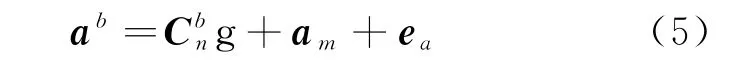
式中：g为重力加速度;am为传感器实际的运动加速度;ea为MEMS加速度计器件输出数据所对应的误差，可以认为是白噪声[13]。

当载体以一定的运动加速度做相对稳定的机动性运动时，可以认为相邻时刻的运动加速度变化在一定的范围之内，可将运动加速度am更新的数学模型定义如下。

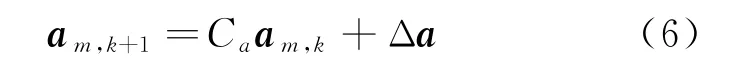
式中：Ca为量纲常数，其取值在0 到1 之间;am，k和am，k+1分别为k时刻和下一时刻的运动加速度的值;Δa 为运动加速度在相邻时间内的变化[14]。

此加速度模型可应用在卡尔曼滤波器的数学模型中，即由上一时刻滤波后得到的运动加速度的最优估计值来反映出下一时刻的运动加速度的先验值，该估计过程如下。

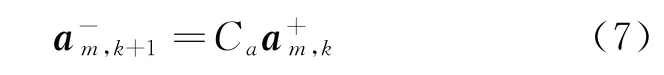
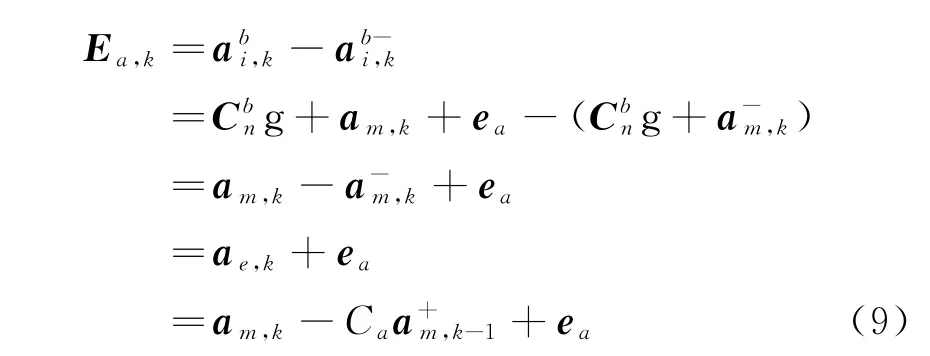
因存在重力加速度，加速度计无法直接测量运动加速度。而在高频的数据采集过程中，相邻时刻的加速度测量值也可认为在一个相同的领域内变化，故传感器实际输出的加速度数据ai，k可以准确的反映出运动加速度am，k的变化情况。故可将公式中的am，k信息利用ai，k来代替，得到加速度测量值与估计值之间的关系式如下。

2.2.2 加速度误差观测量

状态方程只包含加速度信息，故协方差矩阵Ra，k为对角阵，且各元素均为非负值。本课题针对加速度数据的协方差矩阵Ra，k的特点设置了统计量La，k，令该统计量的值为协方差矩阵对角线元素的相加的和(为避免对角阵元素相乘结果抵消的现象，故不采取对角线元素相乘的方法)，当载体进行稳定的机动性运动时，La，k将稳定在一定阈值内。设载体在开始稳定运动前几秒的统

2.2.3 磁强误差协方差

与MEMS加速度计的数学模型类似，电子磁强计输出数据的数学模型可以定义如下。

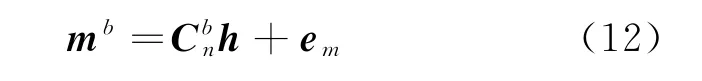
式中：h 为当地地磁场在水平面投影的参考向量;em为磁强计器件的误差噪声，可认为是白噪声。磁强计输出数据的更新方程如下所示。

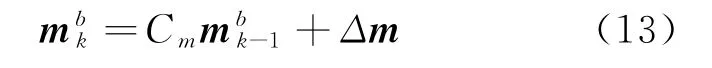
式中：Cm为磁强计数据更新过程所对应的量纲常数;Δm 为相邻时间内磁强向量在各轴投影值的变化。磁强计测量值的最优估计值和其下一时刻先验值的关系如下。

根据前文的分析可以得到磁强计输出的测量数据的协方差Rm，k的表达式如下。

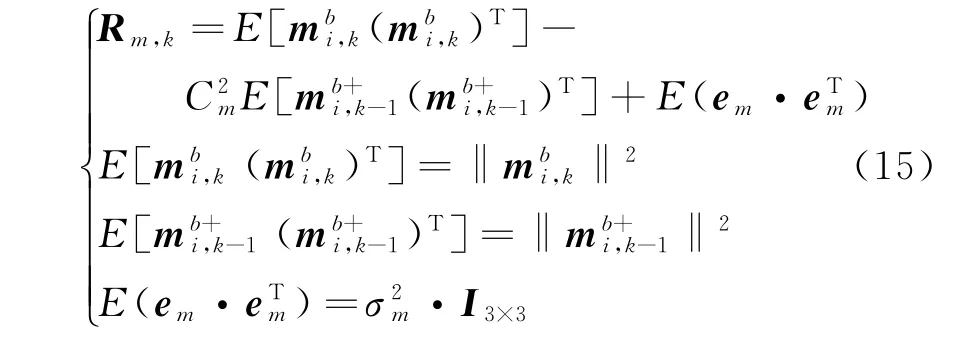
2.2.4 磁强误差观测量

3 实验测试与结果分析

为验证算法的可行性，课题针对设计的航姿系统进行了实物实现，并设计了机动性实验模拟磁干扰环境和强机动运动环境。由于互补滤波姿态解算算法在姿态解算应用中已被证实是一种高效的姿态求解方案，故此实验也将解算结果和互补滤波姿态解算算法的解算结果进行了对比，从而得出算法解算效果的评估。

系统硬件实现应用的传感器为MPU6050和HMC5883磁强计，MPU6050模块中含有三轴陀螺仪和三轴加速度计，各传感器数据通过STM32F103 开发板采集，数据输出频率为50 Hz。姿态解算参考值来自Inertial Labs公司的AHRS-Ⅱ航姿系统。

实验器件安装如图2所示，AHRS-Ⅱ三轴精度均在0.1°左右。为保证测试结果的有效性，AHRS-Ⅱ和本文的航姿解算硬件模块通过PVC透明底板固连，并利用AHRS-Ⅱ对实验用传感器进行了标定。

为模拟航姿系统在有强磁干扰的环境下进行机动运动的情况，本课题针对机动性实验做了如下设计。在航姿系统运动过程中，将带有强磁性的器件靠近运动载体以模拟磁干扰环境，同时将载体进行高频高速的随机运动，使其发生较大较快的姿态变化，运动加速度峰值为1 g。实验时常约为2 400 s，将采集到的数据通过MATLAB进行分析，得到了加速度计误差统计量La，t和磁强计误差统计量Lm，t的变化如图3所示。

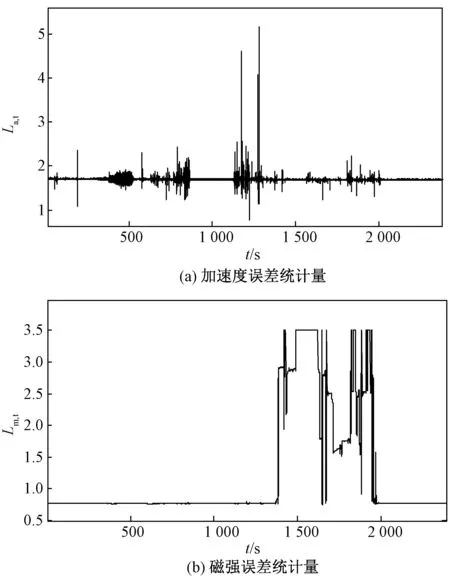
图3 误差统计量

由上图可知，在(800～900)s等时刻航姿系统做机动运动，在(1 100～1 300)s时载体进行强机动运动，故此时加速度误差统计量La，k骤增。在(1 400～2 000)s之间磁强计受到较大的磁干扰，导致磁强数据变得不可用。

姿态解算结果如图4所示(星点线为AHRS-Ⅱ输出的参考值，实线为本文算法的解算结果，虚线为互补滤波算法的解算结果)。

将本文算法和互补滤波算法的姿态结果分别和AHRS-Ⅱ提供的姿态参考值进行做差对比，结果统计如表1所示。

表1 姿态结果误差对比

实验结果表明，载体在磁干扰较强的环境下进行强机动运动时，与互补滤波姿态解算法相比，本课题设计的姿态解算方案提供的横滚角均方误差减小了9%，俯仰角均方误差减小了10%，航向角均方误差减小了38%，使航姿系统输出姿态的精度得到了提升。

图4 姿态角变化示意图

4 结论

文章针对载体在磁干扰较多的环境下进行长时间的强机动运动的情况，结合AHRS航姿系统小型化、低成本的工程实现要求，设计了一种姿态解算算法。该方法利用卡尔曼滤波器对加速度计和磁强计传感器信息进行预处理，建立四元数模型描述姿态，利用梯度下降法对多种传感器信息进行融合与解算，以得到最后的姿态信息。实验结果表明，此算法能利用自身信息对数据进行处理，提升载体在磁干扰较强环境下的强机动运动时的姿态精度，且此算法简化了卡尔曼滤波器模型，结合梯度下降法使得算法的运算量更小，对姿态确定的相关工程应用具有一定意义。