一种数字信号调制特征提取方法

汪 亮， 杨成杰， 王 灿， 蔡 乾

(上海无线电设备研究所，上海200090)

0 引言

近年来，随着软件无线电技术的快速发展，通信侦察、反侦察、对抗等现代化信息技术的研究成为热点。无论在民用领域还是军事领域中，无线电技术都扮演着重要的角色，而电子侦察技术对于民用科技的提升以及国防实力的增强都有着极大的重要性。无线通信利用空间电磁波辐射传输图像、文字、声音等信息，这种开放式的信道环境使得通信对抗侦察成为可能，而信号的调制识别技术也成为电子侦察中的重要手段之一。因此，信号的特征提取与分析成为通信侦查与干扰领域的热点。

在通信侦察与干扰中，通常要求信号调制方式识别技术具有实时性、智能化，这就要求信号的特征提取算法计算复杂度低、具有较大的特征距离以及良好的特征鲁棒性。1995年，A.K.Nandi和E.E.Azzouz等人发表论文[1-2]，通过提取信号在时域和频域上的七个瞬时特征参数来作为信号的识别参数，该算法虽然计算简单，但是在低信噪比下，特征距离小，达不到预期的效果。

2000年，SWAMI A 和SADLER B.M 提 出提取数字信号的累积量特征[3]，构造四阶矩类来实现信号分类[4-5]，但是该算法可识别的信号类型少且鲁棒性差。

2006年，高永强、陈建安通过提取数字信号的矩特征，通过构造特征参数，实现了2ASK、4ASK、8ASK、QPSK、8PSK、16QAM 等多种数字信号的分类识别[6]。2010 年，张弛、吴瑛等人通过对信号进行微分计算[7]，然后提取信号的累积量特征，实现了MFSK 信号和8PSK 信号的分类识别，文献分析结果表明，该算法也能有效地抑制噪声对特征的影响。本文主要对数字信号进行Wigner-Ville时频变换的Rényi熵值特征进行了仿真与分析，通过仿真数据表明，本文的提出的三阶Renyi熵值特征具有良好的特征距离与特征鲁棒性，在数字信号识别领域可以有较大应用。

1 信息熵

Shannon借鉴热力学的概念，将离散随机事件出现的概率定义为信息熵，并且给出了信息熵的计算公式。设一个有n 个随机事件的概率系统(X1，X2，…，Xn)，第i 个随机事件Xi出现的概率为Pi(i=1，2，…，n)，且满足特征提取是调制识别的关键步骤，通过对接收信号的变换，使信号之间特征区分明显，尽可能集中表征显著类别差异的模式信息。信息熵能定量描述信号的不确定性，在各个交叉领域应用广泛，如故障诊断、信号识别等。从微观上看，一个系统有序程度越高，则熵就越小，所含的信息量就越大[8]。

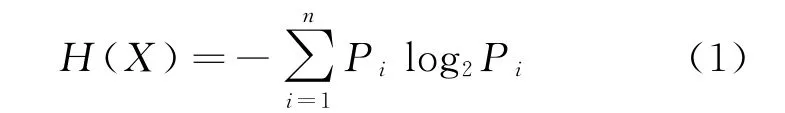
对于连续概率密度分布P(x)，则系统的平均信息量为

在信号分析中，信号的熵值越大，说明信号中奇异点越少，说明信号越稳定。同时，信号的携带信息能力可以通过熵值来进行区分，这也是熵值理论在信号分类识别领域应用的理论基础。

2 基于时频变换的特征提取方法

(1)时频变换分析

Wigner-Ville分布(WVD，Wigner-Vill distribution)是时频信号分析的一种非线性变换，其实质就是将信号的能量分布在一个二维的平面内展开。WVD 分布表达式如下：

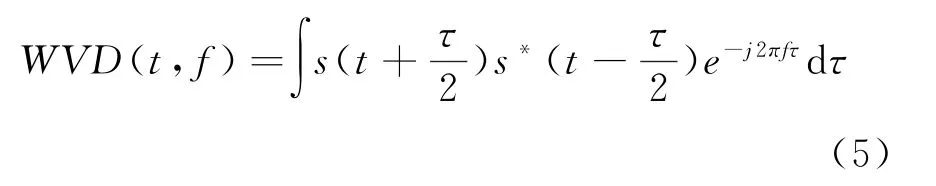
WVD 分布具有很多优良的特性，比如说时移不变性、频移不变性等。但是，它也存在一些不足之处，尤其是对多频率分量的信号的处理，WVD 分布的时频分析会有交叉项的产生，会让真实信号的时频变换波形产生畸变，影响信号的特征分布，这会使得信号的时频分析变得困难[9-11]。

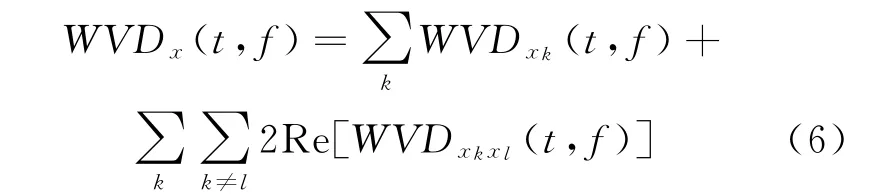
本文采用Cohen 类时频分布中的平滑伪Wigner-Ville分布。图1 是4FSK 信号平滑伪Wigner-Ville分布时频变换仿真图。

对变量t 和τ 分别进行加窗函数h(τ)和g(τ)做平滑即可得

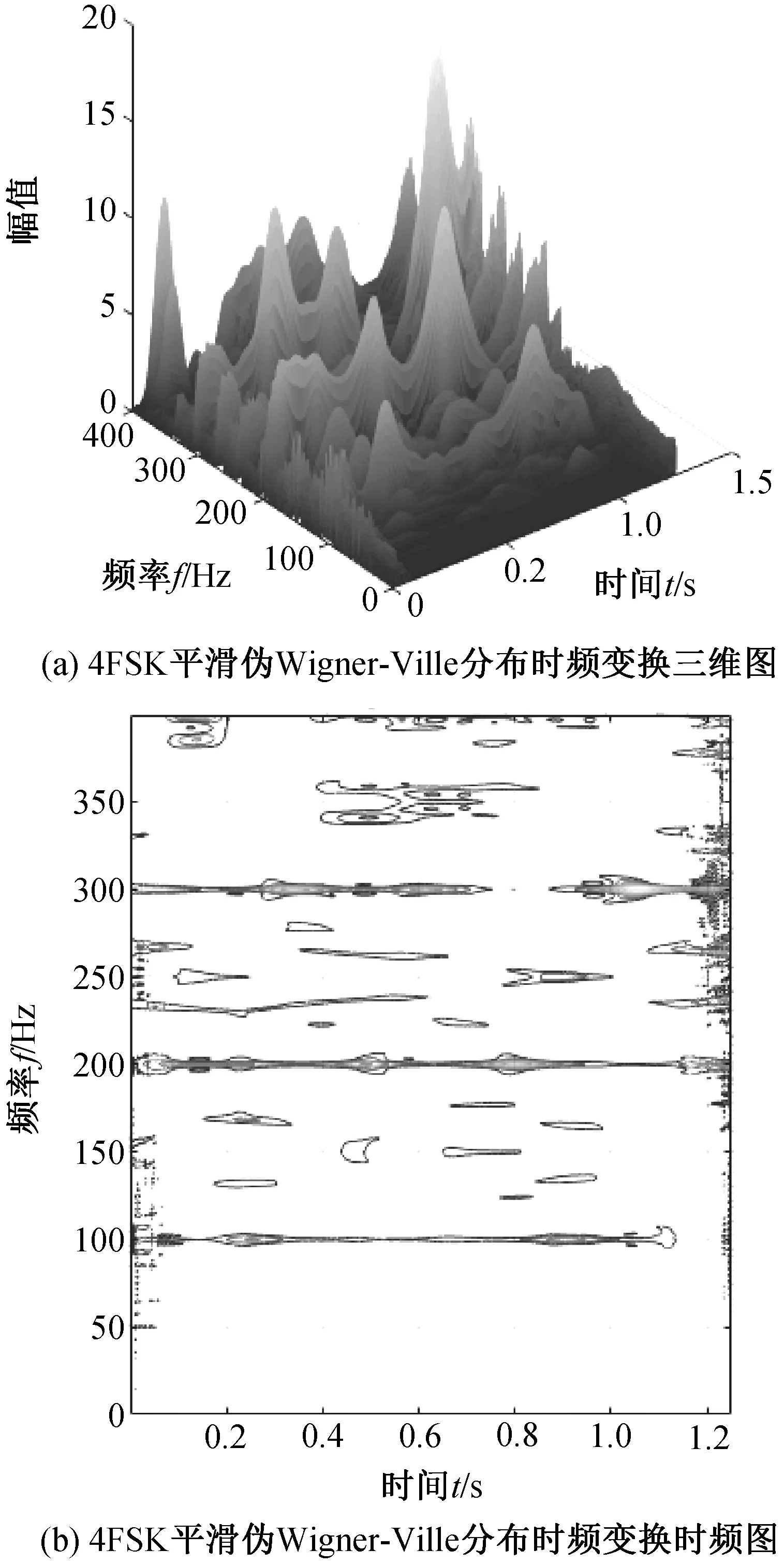
图1 4FSK 信号平滑伪Wigner-Ville分布时频变换仿真图

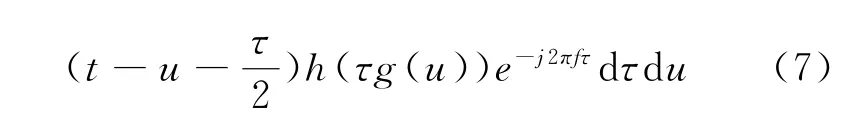
式中：h(τ)和g(τ)是两个实的偶窗函数，且h(0)=g(0)=1。

(2)Rényi熵值特征提取

信号的时频变换就是将信号的能量分布于时频平面内，信号的能量分布的有序程度以及复杂度可以用熵值来表示。熵值的大小反映了信号在时频域内的能量分布情况[7]，Rényi熵定义如下：

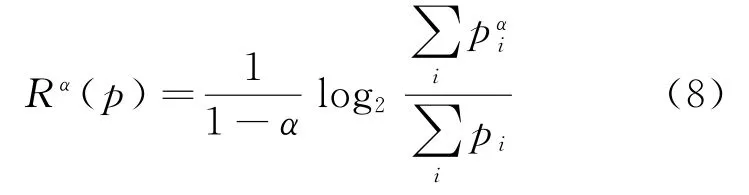
对于连续函数形式的二维概率密度分布分布f(x，y)，其香农熵与α 阶Rényi熵定义分别为

2 基于时频变换的特征提取方法

仿真实验过程中的时频变换采用伪平滑Wigner-Vine分布，仿真过程中信号长度x(t)为2 048个点，码元速率fd=1 000 sps，载波频率fc=4 k Hz，采样频率fs=16 k Hz，传输信道选择AWGN。以BPSK 信号为例，图2是BPSK 信号Rényi熵值特征提取的流程图。

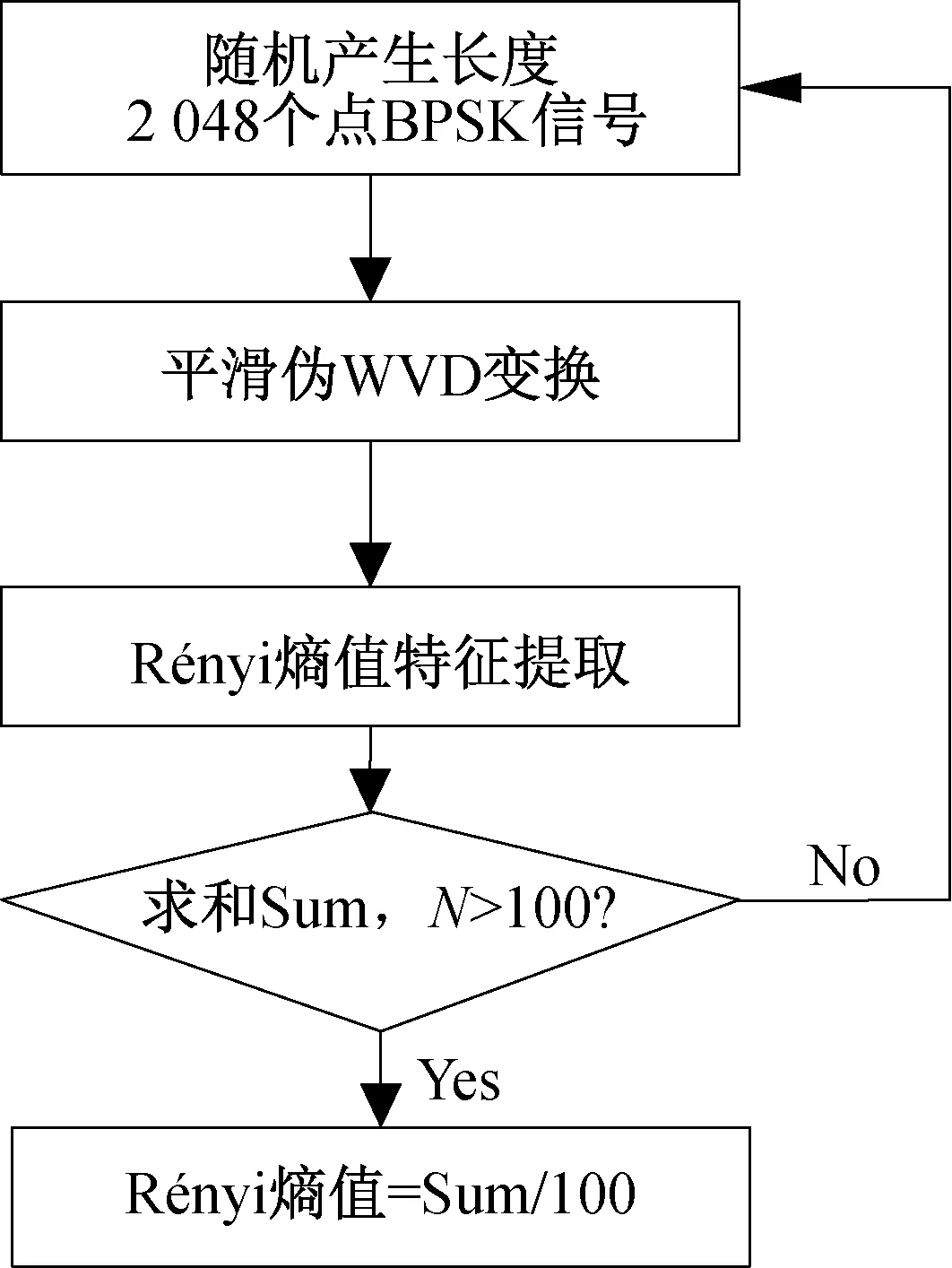
图2 数字信号Rényi熵值计算流程

图3是在SNR=5 dB 条件下，每种数字信号进行100次蒙特卡洛实验，数字信号Rényi熵值均值随阶数变化曲线图，图4 是数字信号3阶Rényi熵值特征随信噪比变化曲线图。

因为非整数阶α 的Rényi熵值会产生复数，本文不再讨论。由WVD 分布的分析可知，多频率分析的信号的WVD 分布会产生交叉项，而多分量信号的偶数阶Rényi熵由于交叉项的存在，使得熵值特征产生震荡性[8]。奇数阶的Rényi熵受交叉项影响较小。有学者研究理论分析和仿真表明，在α=3 时绝大多数信号的时频分布满足Rényi熵值公式稳定条件，同时时频分布交叉项的对熵值的影响是渐近为0的[9]。而本文的所用信号中包含多分量信号，因而本文主要考虑稳定性更好的奇数阶α 的情况。图3是常见的数字信号时频分布Rényi熵随奇数阶α 变化情况。从图中可 知，在α=3 时，4FSK、8FSK、16QAM、32QAM 信号的Rényi熵值特征距离较大，具有很好的分类效果，2FSK、BPSK、MSK 信号特征距离较小，但是仍具有一定的可分离性。而QPSK 以及8PSK 信号的熵值特征完全混叠，无法区分。随之α 阶数增加到5 和7 的时候，4FSK、8FSK、16QAM、32QAM 信号的熵值特征距离仍然较大，具有良好的分离性。而其余信号的熵值特征混叠增加，可分离性变差，同时，随着阶数的增加，信号熵值特征的提取运算量指数增加，计算复杂，可操作性较差。因此，综合考虑，当Rényi熵阶数α=3时，熵值的稳定性最好，可以最大程度的提高特征分类效果。

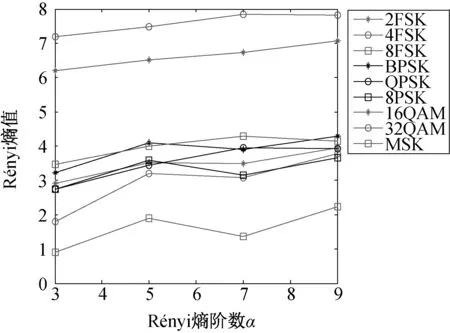
图3 Rényi熵值随阶数α 变化曲线

时频变换可以同时很全面直观地描述信号频域和时域信息，基于时频变换的Rényi熵从信号的时频域来计算信号的复杂度，其信息熵包含了信号时域和频域的。图4可以看出，无论在低信噪比还是高信噪比下，16 QAM 和32 QAM 信号的Rényi熵值都有较大的特征距离。从图中的曲线可以看出，数字信号熵值特征鲁棒性好，特征随噪声起伏小。同时，信噪比大于0 dB时，Rényi熵值特征对于4FSK 和8FSK 信号分类能力也有较好的效果。图4 的熵值特征曲线显示，Rényi熵值特征对于BPSK、QPSK、MSK、8PSK 以及2FSK 信号分离能力有限，但是可以将BPSK、MSK 和2FSK、QPSK、8PSK 信号作为两类信号区分开来。因此，综上所述，基于时频变换的Rényi熵值特征对于16QAM 信号、32QAM 信号、4FSK 信号以及8FSK 信号有良好的分类能力。

图4 3阶Rényi熵值随信噪比变化曲线

4 结论

本文通过对数字信号Rényi熵值特征进行提取，并分析了不同时频变换对熵值的影响，通过仿真分析发现三阶数字信号的Rényi熵值特征具有最佳的特征距离。最后通过对几种数字信号的特征在不同信噪比下的仿真可以看出，本文的数字信号Rényi熵值特征对QAM 信号、4FSK 信号以及8FSK 信号具有良好的区分恩两公里，且信号特征鲁棒性好。说明了本文提出的数字信号调制特征提取方法的有效性。