基于组合频响函数的动力总成刚体模态参数识别*
2019-05-28费振南范让林张楚源屈少举宋鹏俊
费振南 范让林 张楚源 屈少举 宋鹏俊
(1.北京科技大学,机械工程学院,北京 100083;2.东风汽车公司技术中心,武汉 430058)
主题词:动力总成 刚体模态参数识别 组合频响函数
1 前言
动力总成刚体模态是影响整车振动与噪声,特别是怠速NVH性能的重要因素,在悬置系统开发阶段,设计并优化悬置布置位置和动特性、匹配并试验验证刚体模态是提升整车NVH性能的重要手段[1-3]。获取动力总成刚体模态的方法主要有试验模态分析(Experimental Modal Analysis,EMA)、工作模态分析(Operation Modal Analysis,OMA)和数值计算等。Delprete C等[4-5]采用锤击激励和激振器激励的EMA方法识别动力总成模态;Friedmann A等[6-9]采用OMA的方法识别工作状态下的动力总成模态;范让林等[10]在数值计算中采用接地状态下的动力总成6自由度模型对结果进行适当修正,得到整车状态下动力总成刚体模态;上官文斌等[11]建立了考虑车身和非簧载质量的动力总成6、9和13自由度模型,计算并分析了不同自由度模型下动力总成刚体模态频率和能量分布。刚体模态试验通常采用双激振器激励下多输入多输出(Multiple Input Multiple Output,MIMO)的EMA方法,防止由于激励能量不均导致模态参数识别不完整。
本文基于单激振器激励下单输入多输出(Single Input Multiple Output,SIMO)的EMA方法,在不同激励点逐一进行试验,并通过不同激励点的组合频响函数进行刚体模态参数识别,得到了动力总成完整6阶刚体模态,建立了动力总成-抗扭杆12自由度仿真模型,验证了组合频响函数方法的可行性。
2 组合频响函数试验模态分析与流程
2.1 组合频响函数
系统传递函数一般为复值函数,分母为该系统特征方程,其根即为系统极点。根据传递函数的极点,可将传递函数表示为多项分式和的形式,极点包含固有频率与阻尼因子信息,分子留数包含模态振型信息,表明多自由度系统的传递函数可表示为多个单自由度系统传递函数的线性组合[9]。激励点j到拾振点i的跨点频响函数Hij(s)为:

式中,Ci(s)为频响函数的分子多项式;N为模态阶数;sr与为系统极点;Aijr为激励点j作用下拾振点i处的第r阶模态留数;互为共轭。
留数可用拾振点和激励点模态振型向量表示:

式中,Qijr为比例因子;Ψr为激励点j或拾振点i的模态振型向量;Ljr为模态参与因子。
M个激励点的组合频响函数Hi sum(s)定义为:

式中,Hisum(s)中sum表示各激励点的组合。
若各激励点的被测对象和拾振点相同,则测得频响函数的极点和拾振点模态振型向量一致。设激励点1的频响函数只缺少k1阶模态参数,激励点2的频响函数只缺少k2阶模态参数,则两者组合频响函数表达式以及模态参与因子表达式分别为:

式中,各变量中下角标sum表示各激励点的组合。
通过激励点1和激励点2的组合频响函数,可在频域内进行模态参数估计,同时通过留数和比例因子可得到各激励点在各阶模态的模态参与因子大小。
2.2 试验方法与参数识别流程
采用EMA方法对图1所示接地状态下的动力总成进行刚体模态参数识别[12]。该动力总成由钟摆式三点悬置系统支承,左悬置为衬套型橡胶悬置,右悬置为被动式液压悬置,后悬置为抗扭杆悬置。

图1 动力总成刚体模态试验台
动力总成刚体模态试验需满足的边界条件为支承结构的1阶模态频率是被测对象刚体模态上限频率的3倍以上。一般动力总成刚体模态上限频率小于30 Hz,经有限元分析,支承结构的模态频率如表1所示,可知3个支承皆满足刚体模态试验的边界条件要求。

表1 支承结构的1阶模态频率
理论上为了识别动力总成完整6阶刚体模态,特别是有重模态的情况下,应采用MIMO方式,但考虑到工程中激振器数量有限,且旨在探讨基于SIMO的EMA方法,故采用不同激励点组合FRF(Frequency Response Function)的方式识别6阶模态。模态试验及参数识别流程如图2所示。

图2 基于组合频响函数的刚体模态参数识别流程
试验使用Siemens数据采集系统和模态分析软件,采集动力总成表面8个拾振点的三向加速度响应。测试系统和拾振点布置如图3所示。

图3 测试系统和拾振点布置
试验时采用激振器和推力杆组合的方式进行激励,试验激励信号采用猝发随机信号(Brust Random),激励频带包含5~30 Hz带宽内所有频率成分,可平均掉被测结构可能存在的轻微非线性的影响。选取如表2所示3个激励点的模态试验结果进行模态参数识别。RX、RY和RZ是以动力总成质心坐标系为基础,由于激励位置偏心放置而产生的绕X、Y和Z轴的扭矩方向。

表2 激振器的激励位置及方向
3 基于组合频响函数模态参数识别
进行激励信号与响应的相干检查后,通过Ploymax模块手动选择极点的方式识别刚体模态参数。分析频带设定为2~27 Hz,软件设定Rank函数值大于模态阶数,各激励点的稳态图对比如图4所示。

图4 3处激励位置的稳态图对比
由图4可看出,3处激励位置的模态频率一致性较好,但由于单一激励点的激励能量在不同模态上分布不均,导致模态参数识别结果不完整。为得到包含6阶完整刚体模态参数的FRF曲线,对各激励点的频响函数进行组合,组合方式如表3所列。

表3 不同激励点的组合方式
通过稳态图自动极点选择AMPS(Automatic Modal Parameter Selection)方式识别组合频响函数的极点,手动去除含有较少S(Stable:模态向量、振型与阻尼稳定)极点的极点组,不同组合的频响函数稳态图如图5所示。利用稳态图识别3种组合频响函数的模态参数,并利用相对标准差表示不同组合同阶模态频率识别结果的波动程度,若各阶模态频率相对标准差均小于1%,则表明不同组合识别的模态频率一致性良好,3种激励点组合识别模态频率如表4所示。

图5 各组合频响函数的稳态图对比

表4 3种激励点组合识别模态频率 Hz
如图6所示,组合三的组内MAC(Modal Assurance Criterion)矩阵非对角线元素值较小,表明该组合各阶模态振型结果正交性良好,无相似模态。以组合三为参考,分别计算激励点组合一和组合二与该组的组间模态置信矩阵MAC,验证各组模态振型的相似性。各组间MAC矩阵的主对角线元素如表5所列。由表5可知,主对角线值大于75,表明不同激励点组合识别的同阶模态振型结果一致。以上试验数据表明,组合频响函数能够准确识别动力总成完整6阶刚体模态频率与振型。
以组合三为例,计算各激励点在各阶模态的模态参与因子,如图7所示。由图7可看出,激励点2#能够有效激励多阶刚体模态,是较为有效的激励点,同时也说明了通过组合频响函数能够衡量不同激励点对各阶模态的激励有效程度。

图6 组合三组内MAC矩阵

表5 组合三与其它组合的组间MAC主对角线值
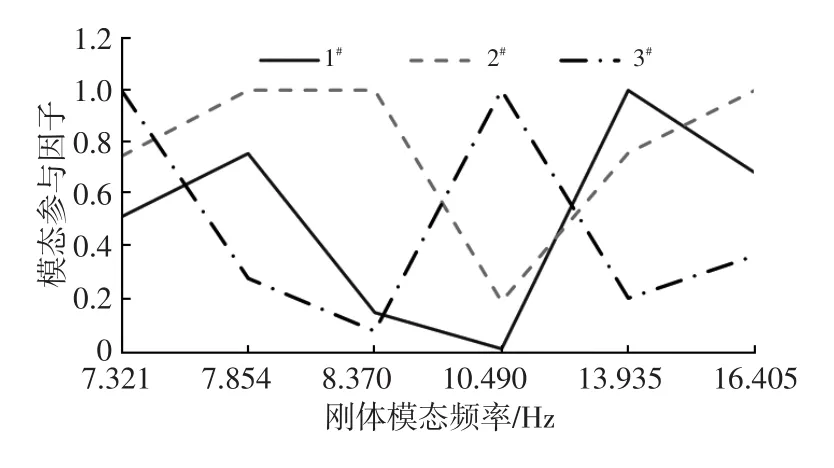
图7 3个激励点的模态参与因子对比
4 含抗扭杆动力总成系统刚体模态仿真
利用ADAMS建立动力总成-抗扭杆12自由度模型,通过仿真得到模态参数结果,并与试验模态结果进行对比,验证基于组合频响函数识别6阶完整刚体模态的可行性。
4.1 12自由度ADAMS仿真模型建立
通过三线摆试验台[13]测得动力总成的质量、质心位置和转动惯量等刚体动力学参数,通过三维模型计算抗扭杆的刚体动力学参数,其中质量m和转动惯量J的测试结果如表6所示。

表6 动力总成与抗扭杆的质量和转动惯量
在动力总成质心坐标系下测得各悬置的弹性中心位置与倾角,如表7所列。悬置元件可简化为3个弹性主轴方向具有线刚度和扭转刚度的弹性元件。选取怠速激励主要频率为25 Hz时的悬置动刚度作为悬置刚度参数,如表8所列。

表7 各悬置在动力总成质心坐标系下的位置与倾角

表8 各悬置在动力总成质心坐标系下的动刚度
根据表6~表8中动力学参数,在软件ADAMS中建立动力总成-抗扭杆12自由度仿真模型,如图8所示。通过ADAMS的Modal Energy Computation模块计算动力总成6阶刚体模态频率,并根据各自由度能量所占百分比判断模态振型。

图8 动力总成-抗扭杆12自由度ADAMS模型
同样在MATLAB中建立动力总成-抗扭杆12自由度模型[14],以验证ADAMS模态仿真结果的正确性,模态计算结果如表9所列。由表9可知,二者的模态频率与振型结果完全一致。

表9 12自由度模型的刚体模态仿真结果
4.2 仿真与试验结果对比
通过对基于组合频响函数的模态试验结果与基于12自由度模型的模态仿真结果的比较,验证组合频响函数识别刚体模态参数的可行性,结果如表10所列。由表10可知,试验结果与仿真频率吻合较好,主振动方向完全一致,表明通过单激振器多点激励以及不同激励点组合频响函数的方式识别6阶刚体模态具有可行性和准确性。

表10 试验结果与仿真结果对比
5 结束语
通过不同激励点的组合频响函数,得到了模态频率一致、振型正交性良好的完整6阶刚体模态参数,并通过模态参与因子衡量了组合内各激励点的激励有效程度。基于完备的动力总成刚体动力学参数,建立了动力总成-抗扭杆12自由度模态仿真模型。试验与仿真结果表明,两者的模态频率吻合良好,主振动方向完全一致,即通过组合频响函数识别完整6阶刚体模态是可行的,且参数识别准确。
