基于曲率控制的紧急避让路径跟踪研究＊

王健 王金波 彭欣 邱绪云 李爱娟

（山东交通学院，济南 250357）

主题词：紧急避让 自抗扰控制器 复合控制 曲率控制 外界干扰

1 前言

作为一项主动安全技术，紧急避让技术可在遇到前方障碍物时帮助驾驶员快速无碰撞地进行避让，同时保证车辆行驶稳定性。紧急避让技术融合了传感器技术、计算机技术与现代信息技术，利用毫米波雷达、激光雷达、高速摄像机检测自车与前方障碍物之间的纵向和侧向距离、纵向速度和加速度，自动规划出避让路径，通过主动控制车辆前轮转角完成转向操作[1-2]。

针对前轮主动转向路径跟踪问题，国内外学者采用PID控制、最优控制、鲁棒控制等方法进行路径跟踪控制器设计[3-4]。PID控制简单，但外界环境发生改变时自适应能力差；最优控制和鲁棒控制算法复杂，不利于工程应用，且控制效果很大程度上依赖于被控对象模型的精度。

中科院韩京清教授提出的自抗扰控制（Active Dis⁃turbance Rejection Control，ADRC）能够观测并补偿外界干扰，保证路径跟踪的鲁棒性[5-11]。本文以规划的理想避让路径曲率和车辆实际行驶路径曲率作为输入，设计二阶自抗扰曲率跟踪控制器，为了加快跟踪速度，采用前馈与反馈控制相结合的复合控制方法进行曲率控制。基于曲率设计的路径跟踪控制器能够保证车辆在紧急避让工况下，抵抗由于路面附着系数变化引起的外界干扰。

2 车辆动力学模型及路径规划

2.1 车辆动力学模型

车辆2自由度动力学方程能够较为准确地反映车辆的横向动力学特性[12]。为了使设计的控制器便于工程应用，本文以2自由度车辆动力学模型（见图1）为基础，设计路径跟踪控制器。忽略转向系统的影响，直接以前轮转角作为输入；忽略悬架的作用；忽略路面不平度和空气阻力影响。

图1 车辆2自由度模型[12]

车辆2自由度动力学方程可以表示为：

式中，m为整备质量；Iz为车辆横摆转动惯量；lf、lr分别为车辆质心到前、后轴的距离；ay为车辆质心处侧向加速度；FY1和FY2分别为车辆前、后轮胎受到的侧向力；γ为车辆质心横摆角速度；δf为前轮转角。

车辆前、后轮侧偏角α1、α2以及质心侧偏角β和横摆角速度γ满足：

式中，u为质心处纵向速度。

2自由度车辆动力学状态方程可以表示为：

式中，cf、cr分别为前、后轮侧偏刚度。

2.2 路径规划

车辆要完成紧急避让过程，其驶过的轨迹类似双移线，避让轨迹需满足车辆动力学特性，需限制侧向加速度，保证避让完成后车身偏航角与水平方向平行，同时需要满足避障约束、曲率连续约束、转向速度约束[13-14]。

如图2所示，以车辆质心为参考点，避让路径分为2个阶段，两阶段为对称关系。其中：R1为车辆质心转弯半径；dy为车辆右前方与前方障碍物不发生碰撞要求的侧向位移；dx为车辆质心侧向位移到达dy时行驶的纵向位移；Ssteer为最小避让距离；θ为车辆质心转过的角度；yH为障碍物左侧宽度；yE为完成整个避让过程的侧向位移。车辆在避让过程中，侧向加速度限制在0.67μmg（μm为路面附着系数，g为重力加速度）以下，由图2可得[15]：

式中，V为车辆质心处纵向速度。

图2 避让路径[15]

V=30 m/s、μm=0.8、yH=1.75 m工况下的路径规划结果如图3所示。

图3 避让路径及其曲率变化

3 曲率跟踪控制器设计

车辆路径跟踪控制器由前馈控制和反馈控制组成。其中前馈控制由车辆等速行驶时稳态横摆角速度增益得到，稳态横摆角速度增益为：

前馈前轮转角δff为：

式中，Wsg=LK；ρ为车辆稳态行驶下的路径曲率。

反馈控制输入为理想避让路径曲率和车辆实际行驶路径曲率，控制器输出为附加前轮转角。对式（4）进行拉普拉斯变换，得到横摆角速度相对于车辆前轮转角的传递函数为：

对上述方程进行拉普拉斯反变换可得：

其中，车辆横摆角速度与路径曲率之间满足：

由式（10）和式（11）可得：

其中二阶自抗扰控制器和前馈+反馈控制器分别如图4和图5所示。

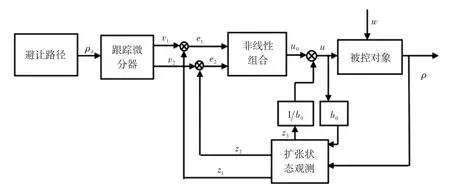
图4 二阶自抗扰控制器

自抗扰控制器由跟踪微分器、非线性组合、扩张状态观测器组成。其中，跟踪微分器能够提取理想输入的一阶导数，并对输入信号进行滤波处理，扩张状态观测器能够观测并补偿外界干扰部分。

图5 前馈+反馈控制器

3.1 跟踪微分器

跟踪微分器是一个非线性动态环节，它能够快速无超调地跟踪输入信号并给出输入信号的微分，跟踪微分器离散化形式为：

式中，fhan可以表示为：

式中，ρd(k)为理想曲率；r和h分别为速度因子和仿真步长；v1(k)和v2(k)分别跟踪ρd(k)和ρ˙d(k)。

3.2 扩张状态观测器

扩张状态观察器将模型不确定性及外界干扰看作一个整体扰动量，通过扩张的状态观测器将其观测出来，其离散表达式可以描述成：

式中，z1(k)、z2(k)和z3(k)为扩张状态观测器输出。

非线性函数fal(e(k),a,δ)可以描述为：

式中，a1、a2、δ和b0为设计参数；和为扩张状态观测器增益[14]。

3.3 非线性组合

非线性组合实质是一种非线性状态误差反馈控制律，实际上是一个非线性PD控制律，可以用离散形式描述：

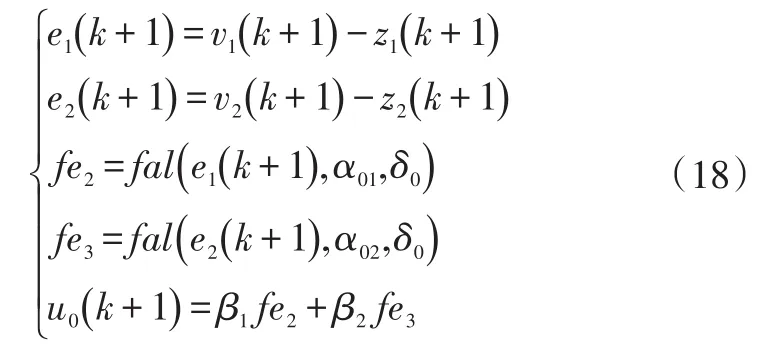
式中，β1、β2、α01、α02和δ0为设计参数。

4 联合仿真验证

为了验证控制器的控制效果，进行不同工况下联合仿真验证。车辆动力学仿真软件CarSim能够模拟真实车辆动力学特性，具有使用方便、运算迅速、仿真精度高等优点。图6所示为CarSim和Simulink联合仿真结构框图。

图6 联合仿真框图

利用CarSim提供的某款C-Class Hatchback车型进行控制器联合仿真验证，车辆主要参数如表1所示。

表1 车辆参数

4.1 对接路面工况

车辆以纵向速度30 m/s在对接路面进行紧急避让路径跟踪测试，其中CarSim可以方便地设置路面附着系数，图7所示为CarSim建立的对接路面3D图。

图7 对接路面3D图

经不断调整，得到自抗扰控制器参数为：r=120，h=0.001，β01=600，β02=1.2×105，β03=8×106，a1=0.5，a2=0.5，δ=0.5，b0=15，β1=1.5，β2=2，α01=0.25，α02=1，δ0=0.01。图8所示为车辆在对接路面的紧急避让路径跟踪结果，车辆在对接路面行驶时，基于曲率设计的跟踪控制器能够控制车辆跟踪规划的理想避让路径。

图8 路径跟踪结果

图9所示为CarSim给出的紧急避让过程中车辆左、右前轮转角变化曲线，整个避让过程中车辆实际行驶路径曲率能够快速、准确、无超调地跟踪规划的理想曲率。图10所示为车辆实际行驶曲率跟踪理想规划曲率结果，整个避让过程中路面附着系数变化引起的外界干扰量可以通过扩张状态观测器观测获得，如图11所示，自抗扰控制器能够补偿干扰量，保证路径跟踪鲁棒性。

图10 路径曲率变化

图11 扩张状态观测器输出扰动量

自抗扰控制器需要调节参数多，参数整定困难，但一经调试完成后不需要进行二次调整，在自抗扰控制器参数不变的情况下，进行对开路面测试。

4.2 对开路面工况

以纵向速度30 m/s在对开路面行驶，利用CarSim提供的轮胎与路面附着系数接口IMP_MUX_L1、IMP_MUX_R1、IMP_MUX_L2、IMP_MUX_R2可以设置车辆两侧路面附着系数，路面附着系数变化如图12所示。

图12 路面附着系数变化

图13所示为车辆在对开路面进行紧急避让路径跟踪时的跟踪结果，从图13中可以看出，车辆在对开路面行驶时，基于曲率设计的跟踪控制器能够控制车辆跟踪规划的理想避让路径。

图13 路径跟踪

图14所示为CarSim给出的紧急避让过程中车辆左、右前轮转角变化曲线，整个避让过程，车辆实际行驶路径曲率能够快速、准确、无超调地跟踪规划的理想曲率。图15所示为车辆实际行驶曲率跟踪理想规划曲率结果，整个避让过程中路面附着系数变化引起外界干扰量可以通过扩张状态观测器观测出来，如图16所示，自抗扰控制器能够补偿干扰量，保证路径跟踪鲁棒性。

图14 前轮转角变化

整个紧急避让过程可以通过CarSim后处理进行仿真演示（见图17），汽车能够安全无碰撞地避让前方车辆及其障碍物。

图15 路径曲率变化

图16 扩张状态观测器输出扰动量

图17 车辆高速避让过程演示

5 结论

基于曲率设计的路径跟踪控制器设计简单，能够保证车辆实际行驶轨迹曲率跟踪理想规划的曲率；基于曲率设计的自抗扰控制器能够观测并补偿外界路面附着系数引起的干扰，保证路径跟踪鲁棒性；自抗扰控制算法简单、便于工程应用，参数鲁棒性强，但是需要调整参数多，参数整定困难。