次梯度外梯度算法求解随机变分不等式
2019-05-27张小娟
张小娟
(重庆师范大学数学科学学院, 重庆401331)
引言
随机变分不等式(Random Variational Inequalities,SVI)问题已经被广泛应用到经济、供应链网络、交通运输和博弈论等领域[1-2]。本文考虑SVI问题:找到x*∈X使得:
(x-x*)TF(x*)≥ 0,∀x∈X
(1)
其中,X⊂n是非空闭凸集,映射F:n→n且F(x):=E[f(x,ξ)],ξ∈Ω是某概率空间(Ω,F,P)的一个随机变量,E[f(x,ξ)]是数学期望,f(x,ξ)是一个连续映射。
目前求解问题式(1)最常用的方法主要有两类:其一是样本均值逼近(Sample Average Approximation,SAA)[3-4],该法是将Nk个样本函数的均值函数去代替期望值函数,从而在适当的条件下,当k无限增大时证明代替后的问题与原问题等价;其二是随机逼近(Sample Approximation,SA)[5],该法是一种迭代算法,只采用一个样本函数逼近期望值函数,目前很多随机优化问题都是采用该法[6-7]。SA与SAA都是取样本点逼近原问题,但是SA方法每次取的样本个数少,且数值表现好于SAA,因此,本文主要考虑SA方法来解问题式(1)。
基于投影型的SA方法分为一次投影和两次投影。一次投影迭代格式简单,但是理论不好[8-10]。两次投影理论和数值结果好于一次投影,因此本文关注两次投影即外梯度方法。最近Kannan等人[11]提出了基于外梯度的SA方法来求解问题式(1)。其迭代格式为:
yk=ΠX[xk-αkf(xk,ξk)]
xk+1=ΠX[xk-αkf(yk,ηk)]
其中,αk>0是步长;ξk、ηk是来自随机变量ξ的样本,并且独立同分布。在F伪单调并且F有界或者Lipschitz连续下依概率1收敛。Iusem等人[12-13]提出用样本均值的外梯度方法求解问题式(1),在F伪单调并且Lipschitz连续下依概率1收敛。虽然外梯度方法理论好于一次投影,但当投影难以计算的时候,此法计算代价大。本文受确定型问题的次梯度外梯度方法[14]的启发,将基于外梯度的SA方法的第二次投影改投在一个半空间上,提出用基于次梯度外梯度的SA方法来求解问题式(1),并且新的迭代点是第k步和矫正步的一个凸组合,在适当的假设下获得全局收敛性。
1 预备知识
定义1[1]设X⊂n是非空闭凸集,点y∈n到X上的投影为:
定义2[1]对任意的x∈n和α>0,定义问题式(1)的剩余函数为:
当α=1时,剩余函数简记为r(x)。
引理1[1]x*是问题式(1)的解,当且仅当对任意α>0有:
x*=ΠX[x*-αF(x*)]
引理2[1]给定x∈n,对α∈(0,∞),函数α|→是不增的。
引理3[1]设X⊂n是非空闭凸集,有:
(1)对任意的
(2)对任意的x∈n,y∈X,(x-ΠX(x))T(y-ΠX(x))≤0。
(3)对任意的
引理4[15]设对任意的x,y∈n,λ∈(0,1)有:

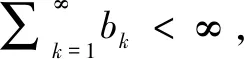

2 算法及其收敛性
投影算法迭代格式在解决SVI问题时方法简单且效果较好,本文考虑用此法解决SVI问题。目前用投影算法解决问题式(1)的相关文献甚少,自从文献[8]提出基于基本投影的SA方法来求解SVI问题后,就有学者提出基于外梯度的SA方法来求解SVI问题。众所周知当投影难以计算的时候,外梯度就受限制,而基本投影反而有利,但基本投影理论本身具有局限。为此,本文考虑采用修正外梯度算法,并受次梯度外梯度算法的启发,提出用基于次梯度外梯度算法的SA来求解SVI问题,将第二次投影改投在一个半空间上,并且充分利用已知点信息,新的迭代点为第k步和矫正步的一个凸组合。
次梯度外梯度算法步骤为:
Step0选择初始点x0∈n,γ>0,θ,δ∈(0,1),初始样本点令k:=0。
Step1给定xk,产生来自Ω的样本ξk,计算xk=ΠX[xk-f(xk,ξk)],停止,否则转Step 2。
Step2计算:
(2)
这里的α∈{γθl,l∈∪0}使得下式成立的最大α为:
(3)
构造半空间Sk:
Sk:={ω∈n|(xk-αkf(xk,ξk)-yk)T×
(ω-yk)≤0}
(4)
产生来自Ω的样本ηk,计算:
tk=ΠSk[xk-αkf(yk,ηk)]
xk+1=δxk+(1-δ)tk
(5)
令k:=k+1,转Step1。其中,αk>0是步长;ξk,ηk是来自随机变量ξ的样本,并且独立同分布;Sk为构造的半空间。新的迭代点为一个凸组合的形式。定义由算法产生的随机误差:
为了获得收敛性本文做如下假设:
假设1问题式(1)的解集X*:=S(F,X)非空。
假设2设F:X→n是伪单调的,即对任意的x,y∈X有:
(y-x)TF(x)≥0⟹(y-x)TF(y)≥0

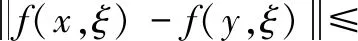


引理5若假设1-3成立,对任意的k∈N算法产生的序列{xk}满足:
(6)
证明通过假设2和引理3可得到:
2αk(tk-xk)Tf(yk,ηk)=
2αk(tk-yk)Tf(yk,ηk)-2αk(yk-xk)Tf(yk,ηk)=

(7)
由于x*∈S(F,X)和F是伪单调的,则有(yk-x*)TF(yk)≥0,则:
(tk-x*)TF(yk)≥(tk-yk)TF(yk)
由于tk∈Sk以及式(4),则有:
(tk-yk)T(xk-αkf(xk,ξk)-yk)≤0
(8)
因此,通过式(8)得到:
(tk-yk)T(xk-αkf(yk,ηk)-yk)=
(tk-yk)T(xk-αkf(xk,ξk)-yk)+
αk(tk-yk)T(f(xk,ξk)-f(yk,ηk))≤
αk(tk-yk)T(f(xk,ξk)-f(yk,ηk))
(9)
通过式(7)和式(9)得:
(10)
通过式(5)、式(10)和引理5,有:

(11)
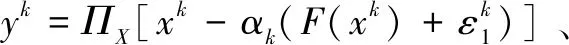

因此,有:
(12)
结合式(11)和式(12),有:
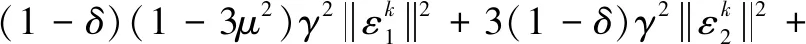
引理6如果假设2成立,算法在k+1不终止,有:

证明如果γ满足式(2),则αk=γ,否则有:
(13)
由假设2成立得到:

(14)









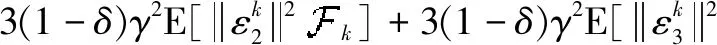
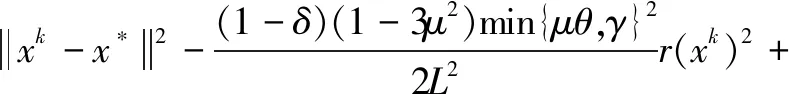
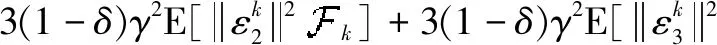

通过假设3和定理1,令:
ak:≡0




3 数值试验

例1考虑问题式(1),ξ是均匀分布在Ω=[0,1],X=+×+×+且有:
例2考虑问题式(1),ξ是均匀分布在Ω=[0,1],X=+×+×+且有:
例3考虑问题式(1),ξ是均匀分布在
有:
例4考虑问题式(1),ξ是均匀分布在
有:
这些例子对任意的ξ∈Ω都有唯一解x*=(0,1,1)T。选择初始点x0=(0,0,0)T。
例1~例4的数值试验结果见表1,其中第二列x*是近似解,第三列是CPU时间。

表1 例1-例4的数值试验结果
从表1中可知,近似解都接近解点(0,1,1)T,由此证明该算法是可行的。
4 结束语
结合确定性变分不等式的投影算法和随机逼近方法,提出用基于次梯度外梯度的SA方法来求解SVI问题,在适当的假设下,F伪单调且Lipschitz连续下获得了依概率1收敛,并且数值试验证明该方法有效。
