基于ARIA的K均值聚类算法研究

王雷， 刘小芳， 赵良军

(四川轻化工大学a.自动化与信息工程学院;b.计算机学院, 四川自贡643000)

引言

聚类分析是数据挖掘的一种重要技术手段，而Kmeans算法是其中最常用的方法之一。曹跃等[1]用Kmeans算法来优化铁矿预配料智能调度；刘倩颖等[2]用Kmeans算法与BP神经网络相结合的方法来进行办公建筑逐时电负荷预测；王亚涛等[3]将Kmeans算法和加权K近邻算法相结合来进行室内WIFI的定位。传统Kmeans算法的聚类结果在很大程度上取决于初始聚类中心，但通常对于未知数据并不能很好地确定其最优的初始中心点，因此，Kmeans算法并不总是收敛于全局最优解，这将对研究造成严重的误导。目前，已经有许多研究着力于解决Kmeans算法易陷入局部最优解的问题，如洪月华用[4]MPI蜂群算法对Kmeans算法进行优化；廖武代等人[5]提出了一种基于人工蜂群优化的K均值聚类算法；此外，Chen Z[6]、Lee J[7]和Diesposti R[8]等人都从群算法具有优秀的全局搜索能力出发，将其与Kmeans算法相结合，以改进Kmeans算法易陷入局部最优解的缺点。

针对Kmeans算法聚类过程中因计算各个数据之间的欧氏距离而耗时和易陷入局部最优解的特点，本文将自适应半径免疫算法(Adaptive Radius Immune Algorithm，ARIA)[9]与传统K均值聚类(Kmeans)算法结合，提出了一种ARIA-Kmeans算法。首先用ARIA算法对原始包含大量冗余信息的数据进行压缩，获得能够代表原始数据分布以及密度信息的内部镜像数据，再用Kmeans算法对这个精简数据集进行聚类，从而能以更少的时间和空间消耗找到全局最优解。

1 算法简介

1.1 自适应半径免疫算法(ARIA)

生物的免疫系统是一种自适应的、自组织的、分布式的系统，是一种能够抵挡外来病原体且具有复杂功能的防御系统，它的一大特点就是用有限的资源对数量庞大且种类多变的病毒入侵进行有效地应对。受此特性的启发，人们设计了一种对多峰值函数进行多峰值搜索和全局寻优的新型算法，称为人工免疫算法。人工免疫网络算法在全局优化、数据压缩领域有着举足轻重的地位，其原型是由Jeme N K[10]提出的，在此基础上，Catro De[11]提出了aiNet算法；Fabricio O等人[12]对aiNet算法的优势与不足进行了详细阐述，指出aiNet算法压缩数据时未充分考虑数据密度信息。George B等人[9]在aiNet的基础上考虑数据的密度信息，提出了ARIA算法。

ARIA算法是一种能够从高冗余度数据中提取包含该数据集密度和空间分布信息的数据集的算法，与传统的主成分提取算法相比，其优点在于在压缩数据的同时，能够保留原始数据的密度信息[9]。因此，用ARIA算法处理获得的数据更能代表原始数据的特征，有利于Kmeans算法进行全局最优解的搜索。

在ARIA算法中，Ag表示抗原集合，Ab表示抗体集合，Ra表示各个抗体的抑制半径，r*为半径乘数，mi为变异比率，decay*为衰减系数，E为密度估计的邻域半径，gen*代表迭代的代数，dim为输入参数(原始数据)的维度，自适应半径免疫算法的实现步骤如下：

(1) 参数初始化，随机生成初始抗体种群Ab。

(2) 对于大小为N的抗原集合AgN×d∈Rd中的每个抗原ag，从当前的抗原集合Ag中选择出与其具有最高亲和力的个体，再根据式(1)进行超突变：

ab*=ab+mi×rand×(ag-ab)

(1)

其中，rand是一个(0,1)之间的随机数。

(3) 更新抗体ab，ab=ab*。

(4) 未被刺激到的抗体淘汰。

(5) 对每个抗体计算其邻域密度den，该密度为以ab为球心，E为半径的超球体内部抗体ag的数量，并记录下最大密度为denmax。

(6) 计算更新每个抗体ab的压缩半径Ra：

(2)

(7) 根据式(3)计算抗体集合中各个抗体之间的欧氏距离，表征其亲密度，距离越大亲密度越小：

(3)

(8) 比较djk与max(abj,abk)，如果两抗体之间的距离小于它们各自抑制半径中较大的一个，就淘汰掉抑制半径较大的一个，将最后没被淘汰的抗体加入记忆抗体集合Abm。

(9) 更新邻域半径，E=average(Ra)，即新的邻域半径E为记忆抗体抑制半径Ra的平均值。

mi=decay*×mi

(4)

否则生成新的集合Ab=Abm+Abd。

(11) 重复上述的步骤(2)～(10)，直到达到迭代次数，输出表征抗原集合内部镜像数据的记忆抗体集合Abm。

1.2 K均值(Kmeans)聚类算法

给定Kmeans算法的数据集，X={x1,x2,…,xm}，其中xi(i=1,2,…,m)是d维的数据，即xi∈Rd，代表数据集X中每个数据有d个属性，xi={xi1,xi2,…,xid}。Kmeans算法要将数据划分为k个簇，即分为k类，可以表示为C={C1,C2,…,Ck}，每个聚类中心为Cj(j=1,2,…,k)。k个聚类中心必须满足以下条件：

(1)Cj≠φ

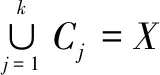
其中，i≠j，Ci∩Cj=φ。按照上述约束条件进行K均值聚类。

(1) 随机产生k个聚类中心C1,C2,…,Ck∈Rd，作为Kmeans算法的初始聚类中心。

(2) 根据式(5)计算每一个样本xi的所属类别Ci，即样本所属类别为与其欧氏距离最小的聚类中心代表的类别：

(5)

(3) 根据式(6)更新聚类中心，将属于Ci的数据xi求几何平均，获得新的聚类中心：

(6)

(4) 不断重复步骤(2)和(3)，直至目标函数解收敛：

(7)

其中，xi为被划分到类别中心cj的数据样本，其意义是描述所有数据样本到它们所属聚类中心的欧氏距离的平方和，其值越小表示聚类划分结果越紧凑和独立，聚类的效果也就越好[13]。

2 ARIA-Kmeans算法实现

2.1 算法思路简介

根据免疫网络和Kmeans算法的应用背景，建立研究数据集X={x1,x2,…,xm}，其中xi(i=1,2,…,m)是d维数据，代表一个抗原对象。依据ARIA的原理，随机创建P个与xi同型的数据作为抗原，在每一次迭代过程中，从抗体集合中选择出与抗原欧氏距离最小的个体对抗原进行表征。完成一次抗原表征之后，淘汰未被刺激的抗原，再计算抗原与抗原之间的欧氏距离，若两个抗原之间的欧式距离小于它们较大的抑制半径，则淘汰抑制半径大的抗体，将其作为冗余抗体信息的表征，由此最终得到能够表征抗原属性的抗体集合。K均值算法将数据集X划分成k个簇，在获得抗体的基础上进行多次聚类，选择出性能最好的中心点作为初始中心点，将Kmeans算法推广到完整数据集上，即可获得目标的聚类结果。

2.2 ARIA-Kmeans算法的实现步骤

(1) 参数初始化，并生成随机的抗体集合。

(2) 根据式(1)和式(2)对初始抗体进行选择、刺激、超突变，未被刺激的抗体被淘汰。

(3) 根据式(3)淘汰集合中冗余的抗体，并更新抑制半径Ra和邻域半径E。

(5) 重复步骤(2)～(4)，直到达到迭代次数，输出记忆抗体集合Abm。

(6) Kmeans算法在Abm上进行聚类，并记录每一次迭代，由式(7)计算得到的目标函数值，直到达到最大迭代次数。

(7) 选用目标函数值最小的聚类中心，作为初始中心。

(8) 扩展到完整数据集，获得更优的聚类中心。

ARIA-Kmeans算法实现流程如图1 所示。

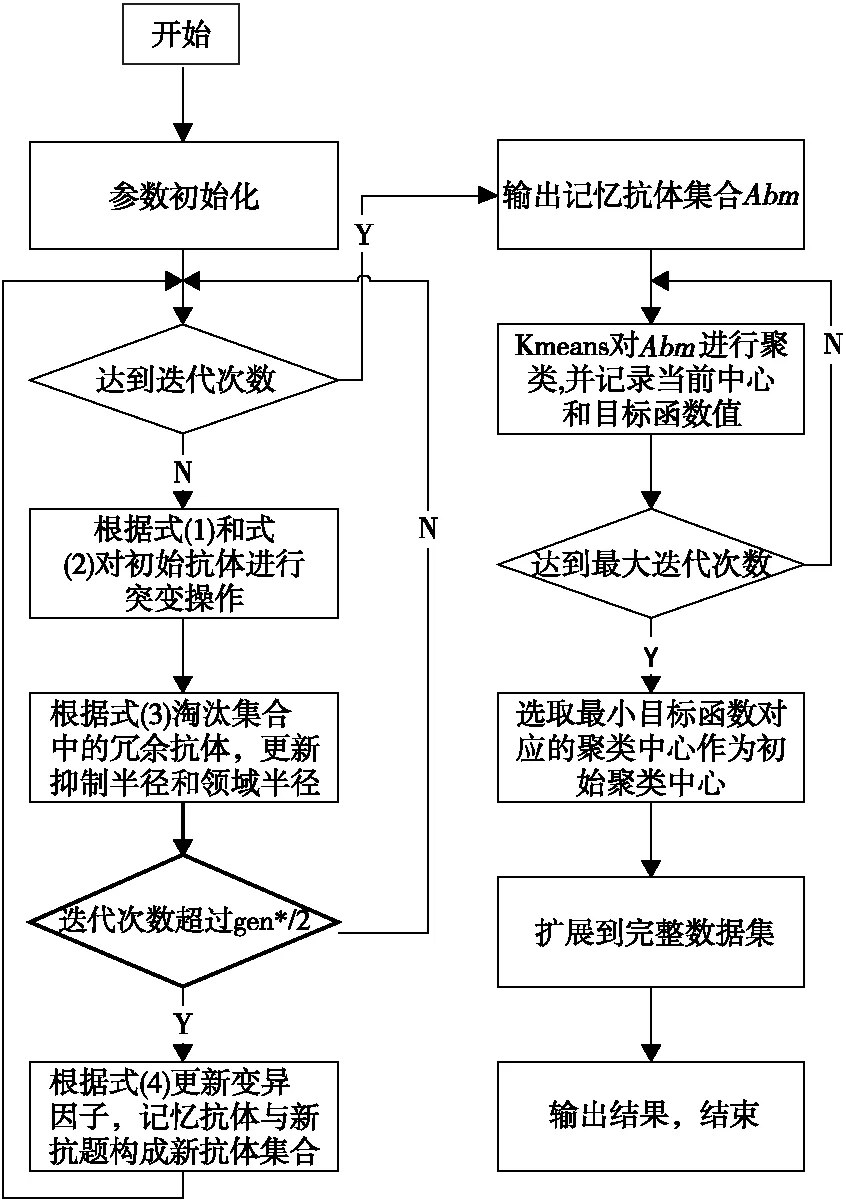
图1 ARIA-Kmeans算法实现流程图

3 实验结果与分析

ARIA-Kmeans算法是从全局最优、运算时间效率、聚类结果稳定度的角度对Kmeans算法进行优化。实验中，将对ARIA-Kmeans和传统Kmeans算法从目标函数收敛值、运行时间、分类正确率及其稳定度4个方面进行对比测试；目标函数收敛值越小越好；运行时间指两个算法分别用于聚类的时间。实验环境：计算机主机i7-6700HQ CPU，主频2.60 GHz，运行内存16 GB；仿真软件为Matlab2016b。ARIA算法对数据进行预处理时，抗体进化代数gen*=50，衰减因子decay*=0.8，突变因子mi=1.0，邻域半径E的初始值随机产生，抑制半径Ra在计算过程中自适应调节。

用4组不同大小的数据集测试算法的目标函数收敛值、时间效率、分类正确率及其稳定度，它们分别包含1500、2500、5000、10 000个数据样本，每一组按高斯分布Gussian=(μ,Cov)，其中参数向量μ为均值，参数矩阵Cov为协方差，聚类中心数为5。5种高斯分布分别如下：

3.1 算法目标收敛值比较

各样本数下，Kmeans和ARIA-Kmeans算法的目标收敛值如图2 ～图5 所示，其中纵坐标为目标函数收敛值，横坐标为迭代次数。

图2 样本1500时Kmeans和ARIA-Kmeans算法的收敛值

图3 样本2500时Kmeans和ARIA-Kmeans算法的收敛值

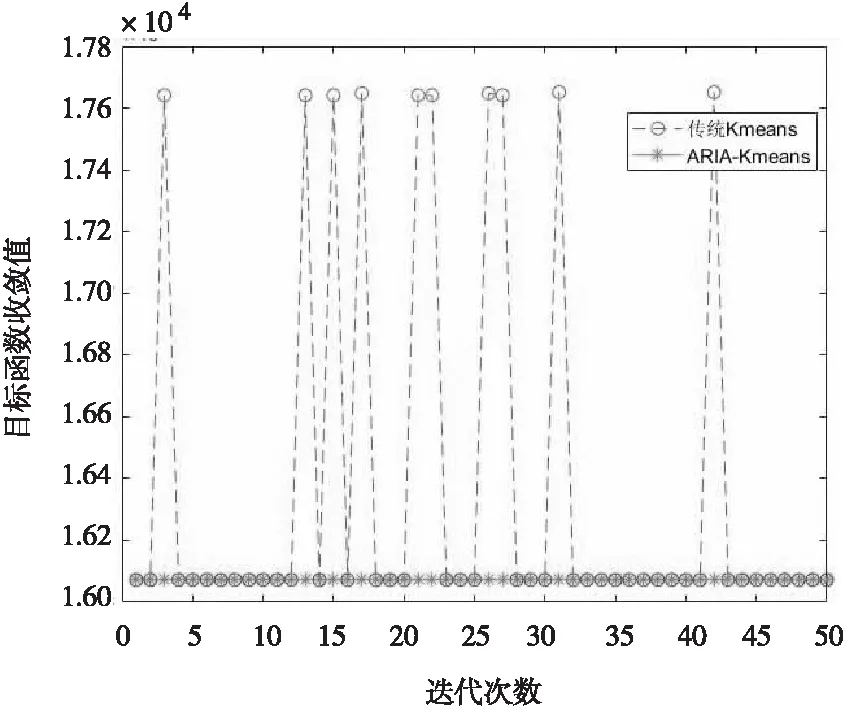
图4 样本5000时Kmeans和ARIA-Kmeans算法的收敛值

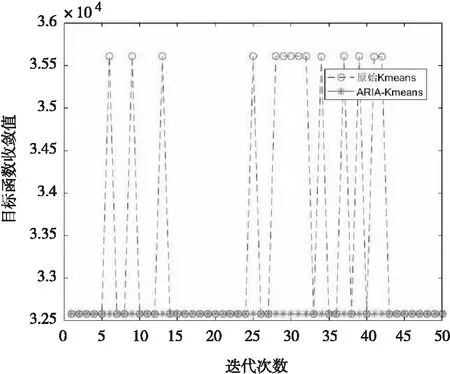
图5 样本10 000 时Kmeans和ARIA-Kmeans算法的收敛值

从图2 ～图5 可知，在50次聚类中，Kmeans算法的收敛值不稳定，时大时小，而ARIA-Kmeans算法的收敛值趋向于一个固定值，目标函数收敛的稳定性好；传统的Kmeans算法由于初始中心不确定，目标函数极易收敛于局部最优，从而得不到理想的聚类结果，而ARIA-Kmeans算法是在预先对原始数据进行压缩得到其内部镜像数据来表征其整体特性之后，再用Kmeans算法对此内部镜像数据进行多次聚类，就可以搜索得到镜像数据的最优聚类中心，然后将此最优聚类中心作为Kmeans算法的初始中心扩展到完整数据集，这样可逼近全局最优的聚类效果，即收敛函数最小。由此可见ARIA-Kmeans算法解决了传统Kmeans算法对初始聚类中心不确定而导致的局部最小问题。

3.2 算法运行时间比较

对上述4组数据进行试验，Kmeans和ARIA-Kmeans算法的运行时间如图6 所示，其中，横坐标表示样本的数量，纵坐标表示目标函数收敛所用的时间。

从图6 可知，样本数为1500、2500、5000、10 000时，ARIA-Kmeans算法目标函数收敛的时间均小于传统Kmeans算法，且随着数据集的增大，两种算法消耗的时间差值越来越大，说明ARIA-Kmeans算法在运行时具有较高的时间效率。

图6 Kmeans和ARIA-Kmeans算法运行时间

3.3 算法分类正确率和稳定性比较

选择样本大小为5000的数据集。考虑到传统Kmeans对初始中心点敏感，且初始中心点随机性较大，因此，聚类次数分别选择了20次、50次、100次。Kmeans和ARIA-Kmeans的平均分类正确率见表1。

表1 Kmeans和ARIA-Kmeans算法的平均分类正确率

用传统Kmeans进行的多次聚类中，由于其初始中心点随机产生，聚类结果的优劣程度参差不齐，少数情况下获得理想的初始聚类中心时，才能拥有较高的分类正确率。在实验中，两种算法获得的最高分类正确率是92.04%。

从表1可知，传统Kmeans算法多次迭代的分类平均正确率低于90.00%，而ARIA-Kmeans算法的分类平均正确率都稳定在91.95%左右，且接近最高正确率92.04%。由此说明ARIA-Kmeans算法的分类正确率不仅稳定，而且是稳定在最高正确率附近；较传统Kmeans算法而言， ARIA-Kmeans算法能获得较高的分类正确率，且分类性能稳定。

4 结束语

本文针对传统Kmeans算法对初始聚类中心敏感，易陷入局部最优和对大数据集聚类速度慢的缺点，提出了一种ARIA-Kmeans算法。实验结果表明，ARIA-Kmeans算法解决了传统Kmeans算法易陷入局部最小的问题。相对于传统的Kmeans算法，ARIA-Kmeans算法能找到更优聚类中心，在保证分类正确率的前提下，提高了算法运行的效率和稳定性，并且聚类数据集越大，这种优势越明显。