基于超效率DEA效益评估的水火电力系统优化调度方式研究
2019-05-27刘文静付仙兰吴杰康
刘文静,付仙兰,吴杰康,沈 娜
(1.华南理工大学广州学院电气工程学院,广东广州510800;2.湖北省孝感市供电公司,湖北孝感432100;3.广东工业大学自动化学院,广东广州510006)
传统的水火电力系统多目标优化调度仍然是目前研究的重点问题,合理的调度方式对于整个电力系统安全稳定、经济运行的尤为重要。因此,实时应对多变的内外界影响因素,合理安排机组出力,选择合适的调度方案,可实现资源的有效配置,提高系统的经济效益。水火电力系统多目标优化调度是复杂的非线性规划问题,传统算法在求解时速度慢且收敛不稳定,智能优化算法[1-3]可随意设置初始点,目前已经成为求解该类大型含有多维约束的非线性规划问题的热点算法。但是智能优化算法容易陷入局部最优或者全局收敛不唯一,文献[4]采用改进粒子群算法对含有多个目标的水火电力系统进行优化调度求解,经多次测算,其最优解并不唯一,而是在一个最优值附近波动,针对该文献存在的问题,提出运用数据包络分析算法对运行结果进行评价择优。将多目标优化问题的多次测算运行结果数据放入超效率DEA模型中评价分析,依据超效率DEA评估值和实际运行状况,得出多个优化调度方案,为决策者提供多个选择。
1 DEA的算法模型
1.1 DEA基础理论
DEA是运筹学、管理科学和数理经济学交叉研究的一个新的领域,是用来评价具有多输入多输出决策单元(DMU)相对有效性的非参数方法,由著名的运筹学家A.Charnes,W.W.Cooper和E.Rhodes于1978年首次提出[5- 6]。
CCR对偶线性规划模型可表示为
θ=minθ
s.t.∑nj=1xjλj≤θx0
∑nj=1yjλj≥y0
λj≥0,j=1,2,…,n
(1)
式中,θ为该决策单元DMUj的有效值(指投入相对于产出的有效利用程度),当θ=1,则该方案有效,θ<1,则方案无效;xj为决策单元DMUj的投入要素,要求越小越好;yj为决策单元DMUj的产出要素,要求越大越好;λj为第j个DMU的权重系数。
1.2 超效率DEA模型
传统DEA模型仅可以评价出有效与非有效的决策单元,但是如果存在多个有效单元,传统模型不能对多个有效的决策单元进行排序。Andersen 和Petersen(1993)提出超效率模型(Super efficiency-DEA)[7]。该模型可对传统DEA模型计算出的效率值进行区分,从而对有效单元进行排序,对于非有效的单元剔除。超效率DEA模型基本思想是进行决策单元效率评价时,用其他决策单元的投入和产出组合替代该决策单元的投入与组合,而其自身被排除在外,其投入导向型模型为[8]
θ=minθ
s.t.∑nj=1,j≠qxijλj+S-i≤θx0,i=1,…,m
∑nj=1,j≠qykjλj-S+k≥y0,k=1,…,r
λj≥0,j=1,2,…,q-1,q,q+1,…,n
S-i≥0,S+k≥0
(2)
式中,θ为超效率评价值,超过1为有效;S-i、S+k为松弛变量值。
2 运用DEA对水火电力系统调度进行评估
2.1 模型选取
利用基本CCR对偶模型及超效率DEA模型两种方法求解含有多个投入多个产出的同质决策单元的效益问题,本文选取模型1和2为效益评价模型。
2.2 评价指标体系的构建
决策单元必须为同质可比的单元,为使数据不失一般性,决策单元取值是在同迭代次数及同维数条件下,将文献[4]的算例数据采用改进粒子群算法进行多次测算,迭代次数为100次,求解程序运行10次后得到的不同运行方式作为决策单元。
投入指标为:耗水量,亿m3;耗煤量,t;排放,t;迭代时间,s。产出指标:发电量,MW。把文献[4]的算例优化运行的结果作为评价指标,将耗水量、耗煤量、迭代时间作为投入指标,污染物排放量、发电量作为产出指标。污染物排放量作为目标之一要求越小越好,但是在DEA中作为产出指标要求越大越好,因此将此指标处理为投入指标。
对于维数相同的多峰值函数,迭代次数越大,越接近最优解,但并非是绝对的,因PSO是一种随机算法,在参数相同的条件下,每次的求解结果也不相等。因此,运用DEA评价算法评估选取合适的调度方案。各评价指标见表1。
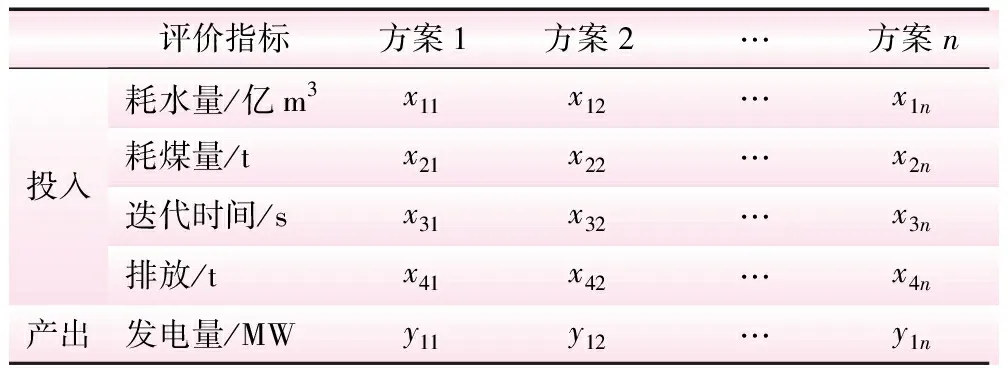
表1 水火电厂的不同调度方案对应的指标
3 算例仿真
3.1算例
论文数据是基于文献[4]对于广西水系在红水河上已经形成的梯级水电站群,对上面的8个梯级水电站以及10个火电站所构成的电网的10个优化调度方案进行效益评估。
3.2 基于DEA及超效率DEA的调度方案效益评估
从表2中可以看出,采用CCR模型计算出2、3、7、8、9五个调度方案θ值均为1,投入对于产出的有效利用率最高,其他方案均为非有效的决策单元。接着采用超效率DEA模型对10个调度方案进行分析计算。由表3及图1可以得出有效的决策单元与采用传统的CCR模型结果一致。同时可以看出方案2是效率最优调度方案,耗煤量较少,水电承担较大负荷,同时迭代时间及排放都较小。但是决策不仅是看方案最终效益的,因为在同样的利益下,有很多种不同的投入量。如,耗水量的不同,耗煤量、排放的不同都是受当时发电情况所影响的。决策者可以根据当前的实际情况或者偏好选取调度方案,决策者可以在不同的外界环境考虑不同的运行方式选择θ值为超过1的超效率DEA值方案。
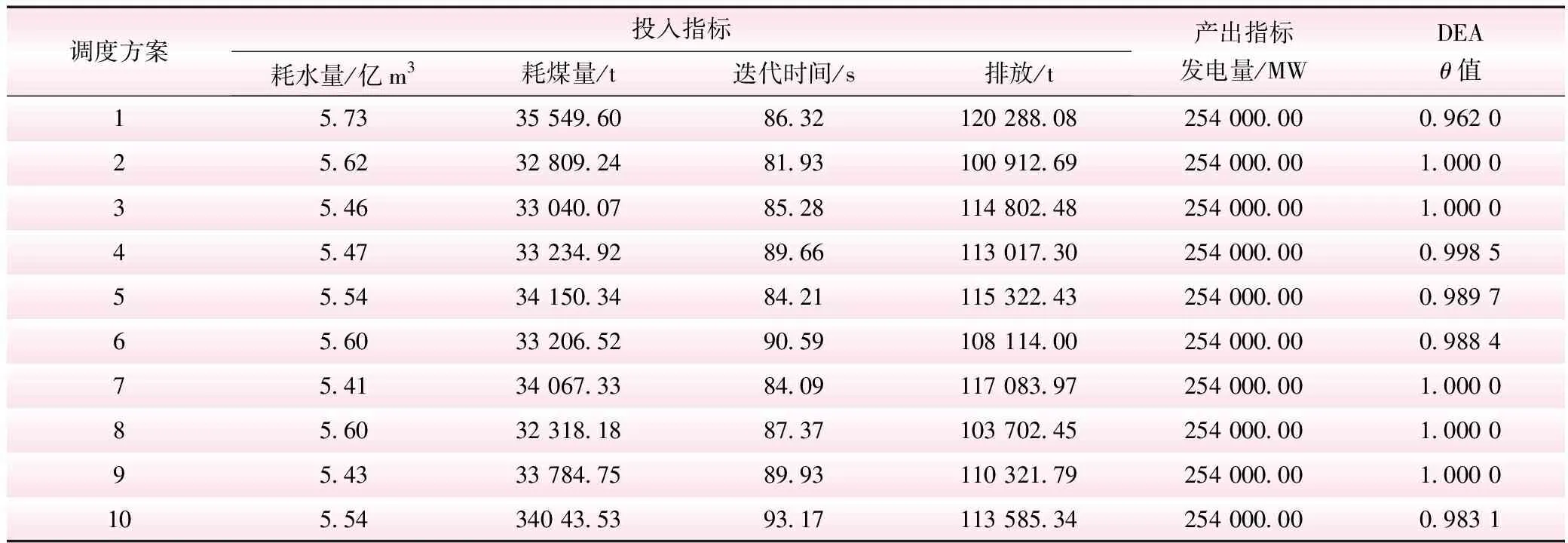
表2 调度方案的DEA模型评价结果
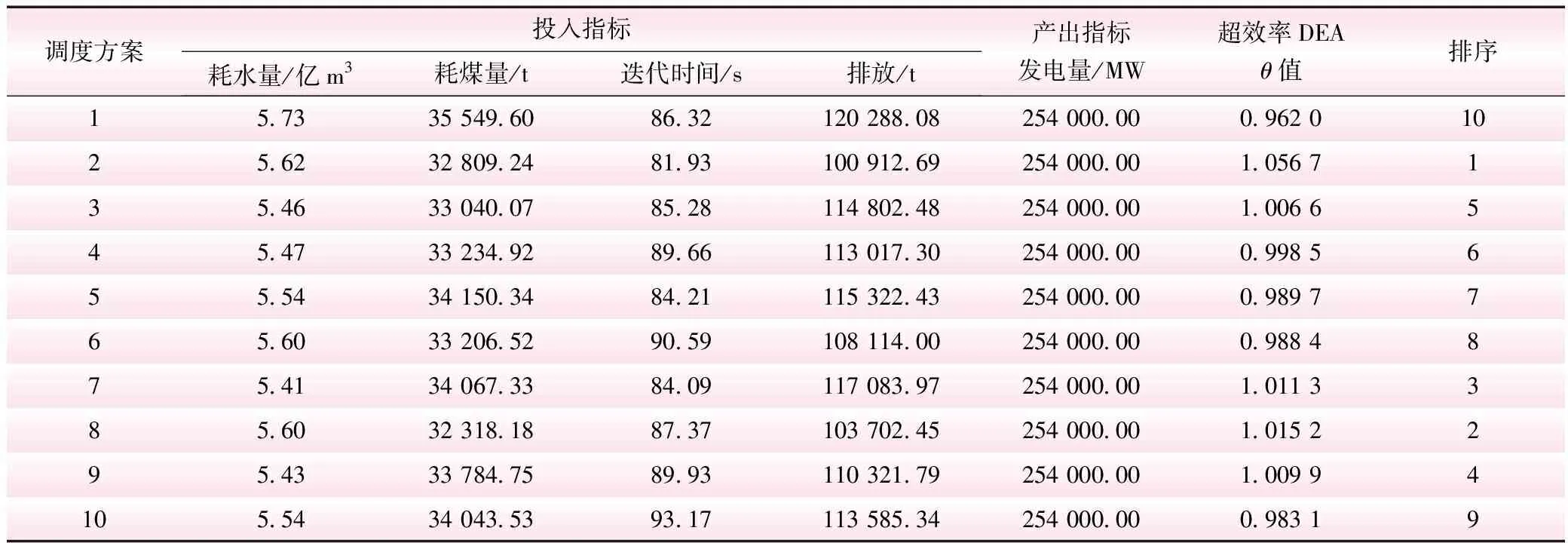
表3 调度方案的超效率DEA模型评价结果
丰大方式运行下,丰水期,即在来水量充足情况下,应首先考虑防洪效益,避免水位过高,应最大程度利用水来发电,减少弃水。以水代煤,节约煤炭资源,可以保护环境,减少环境污染,达到节能减排的效果,可选方案为2和8。
枯小方式运行下,枯水期,即在来水量不足情况下,这时应首先满足航运、灌溉、养殖等效益,水力发电不足,应让可运行的水电机组满发,再利用火电补充。这时水电总出力虽小于火电,但可充分利用水资源,代替了部分火电,在一定程度上也实现节能减排,最终达到了保护环境的目的,可选的方案为3,7,9。
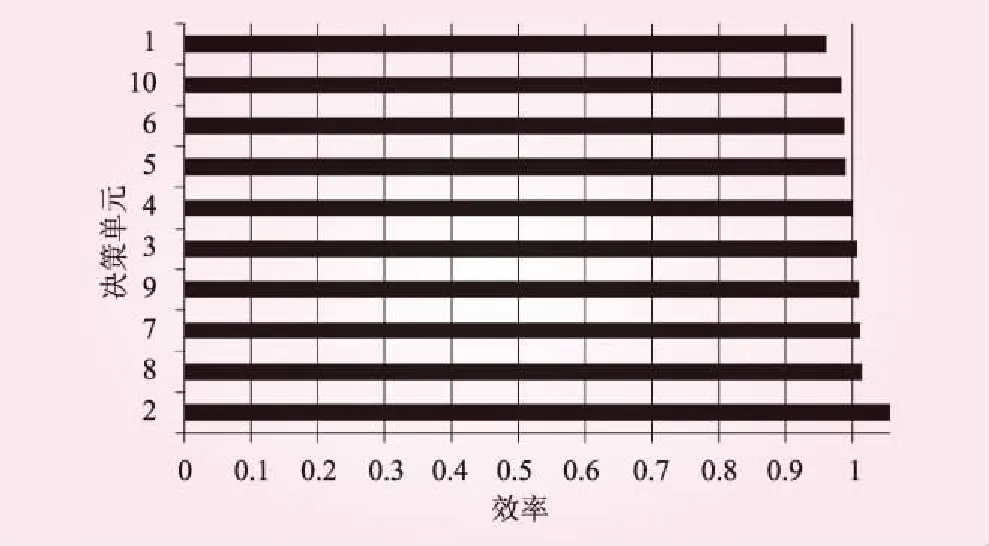
图1 超效率DEA评价结果
4 结 论
本文分别采用DEA和超效率DEA模型对文献[4]改进粒子群优化后的10个水火电调度方案进行效益评估,从而为决策者选择适合的调度方案。实例仿真结果证明该方法的可行性,为决策者提供了优化调度及效益评估双准则的调度方案。体现了节能调度的思想,以水代煤,节约煤炭资源,保护环境。
文章不足之处是投入产出指标考虑不够全面,文中仅将求解结果作为评价指标,不够宏观,决策者在决策时会考虑更多的影响因素,这是本文今后进一步研究的方向。
