基于改进遗传模拟退火算法的BP神经网络的畸变校正研究

(安徽大学 计算智能与信号处理教育部重点实验室，合肥 230039)

0 引言

光学器件由于在实际的生产过程中的失误导致成像原理无法满足小孔成像模型，因此采集得到的图像往往存在畸变现象[1]。镜头畸变对相机的标定精度存在直接的影响，从而影响着后续的测量与三维重建的精度。

现如今，为了得到更好的校正效果，国内外的学者们在该方面做了很多研究。Tsai两步法中首先通过线性标定求解出初始参数，在通过非线性优化求得最终的标定参数与畸变系数[2]。张正友标定法[3]首先通过建立畸变的数学模型，在利用多幅不同位姿的标定板图像完成对畸变参数的标定，但该算法需要通过考虑畸变的种类来建立数学模型。叶峰等对Tsai两步法进行改进，首先选取畸变较小的图像中心位置进行参数的求解，再将焦距和平移分量作为变量，采用迭代的方法逼近精确值。该算法计算较为繁琐，求解过程较为复杂[4]。杨麟等人基于直线的投影还是直线的特性提出利用直线投影特征来对图像进行校正，但该算法需要保证实际场景中必须存在直线[5]。文献[6]提出将图像中的畸变曲线提取出来，通过优化畸变参数来将曲线转化为直线，但该算法模型建立较为困难。以上的这些算法都需要建立数学模型，但由于畸变种类较多，无法建立准确的数学模型，因此本文提出改进的遗传模拟退火的BP神经网络算法来进行畸变校正。该算法无需考虑畸变的数学模型，通过理想点与畸变点作为网络的输入与输出，通过训练得到畸变模型，同时本文采用改进的遗传模拟退火算法对BP神经网络的权值和阈值进行优化，与传统的神经网络相比，加快了网络的训练速度。

1 畸变模型原理

由于实际生产的光学器件成像原理并不满足小孔成像，导致实际投影点与理想像点并不在同一点上，即镜头存在畸变[7]。为了提高图像校正的精度，不仅仅只考虑径向畸变，同时也要考虑切向畸变[8]。因此理想像点(u,v)与实际投影点(Xd,Yd)满足关系如下：

(1)

其中：

(2)

2 基于改进的GA-SA-BP的畸变校正

2.1 改进的BP神经网络算法

传统的BP神经网络采用梯度下降法进行反向传递来对权值和阈值进行修正，但该算法收敛速度较慢，同时精度不高，而LM算法既保留了梯度下降法的优点[9]，同时收敛精度较高，因而采用LM算法对BP神经网络进行改进。

BP神经网络的目标误差函数为：

(3)

其中：n代表输出层的节点总数，yi表示第i个输出节点的期望输出，ci代表第i个输出节点的实际输出，w是一个包含了BP神经网络中所有的权值与阈值的向量。

在神经网络反向传播中，LM算法对网络中权值和阈值的修正量记为Δx，可表示为：

Δx=-[JT(w)J(w)+μI]-1JT(w)e(w)

(4)

其中：J(w)为雅克比矩阵。

2.2 改进的GA-SA算法优化改进的BP神经网络

利用BP神经网络进行畸变校正，无需考虑畸变数学模型，过程简单，但BP神经网络在应用过程中存在收敛速率较慢，易收敛到局部最优解的弊端，难以满足精度上的要求[10]。因而本文采用改进的遗传模拟退火算法优化BP神经网络的权值与阈值，提高BP神经网络的性能。

改进的GA-SA算法优化操作关键性步骤如下。

2.2.1 初始化操作

根据所要优化的参数构成一个向量，然后根据该个体向量随机生成初始种群，因GA-SA算法是对网络的阈值和权值进行优化，因而按照网络的误差构造适应度函数。

(5)

2.2.2 选择操作

传统的遗传算法在选择操作中常采用轮盘选法，但该方法选择随意性太大，在满足既考虑下代种群多样性，也考虑尽可能多的选择好的个体的同时，本文采用分段选择策略与随机抽样相结合的选择操作，设计选择方法如下：

①计算种群的适应度值，同时对其按由小到大进行排序构成新的种群，由适应度函数式(5)所示，适应度值越小，个体基因越好，因而新种群中的个体是按从好到差进行排序的。

②将新种群平均分成好中差3个子种群，在分别从3个子种群中按随机抽样的方法选择一定数量的个体，构成选择操作后的种群，在本文算法中，好中差3个子种群抽取数量的比例按照5:3:2进行选择操作，其目的是为了在保证下代种群多样性的同时尽可能保留好的个体。

2.2.3 自适应交叉和变异操作

自适应交叉操作是以一定的概率Pc来对个体进行重组，生成新的个体，通过调整的值来保证在后代种群进化过程中尽可能保留好的个体基因。

(6)

其中：Pc1，Pc2分别表示初始交叉概率中较大值与较小值，fmin，fave，f分别表示当前种群中的最小适应值，平均适应值及交叉个体中较小的适应度值。

种群中两个个体的交叉方式如下[11]：

(7)

其中:x1，x2为交叉操作前选中的个体，x'1，x'2为交叉操作后产生的新个体，r为[0,1]上的随机数。

自适应变异操作是通过一定概率Pm来对选中的个体进行变异操作，保存种群的多样性，同时通过自适应概率Pm来防止优质个体发生基因突变。

(8)

其中：Pm1，Pm2分别表示初始变异概率中较大值与较小值，fmin，fave，f分别表示当前种群中的最小适应值，平均适应值及变异个体的适应度值。

在变异操作中，对个体采用随机抽样的方法确定个体X中需要变异的基因：xi，然后采用非均匀变异算子[12]对该基因进行变异。

(9)

其中：x'i为基因xi变异后得到的基因，G，Gmax分别为当前进化代数和算法中总的迭代次数；r1为(0,1)上的随机数，ai,bi为该变异基因取值范围的最小和最大值。

2.2.4 模拟退火局部优化操作

为了避免遗传算法易于收敛到局部最优的情况，在种群趋于稳定时，进行模拟退火[13]再优化操作。判断种群是否趋于稳定的条件如下：

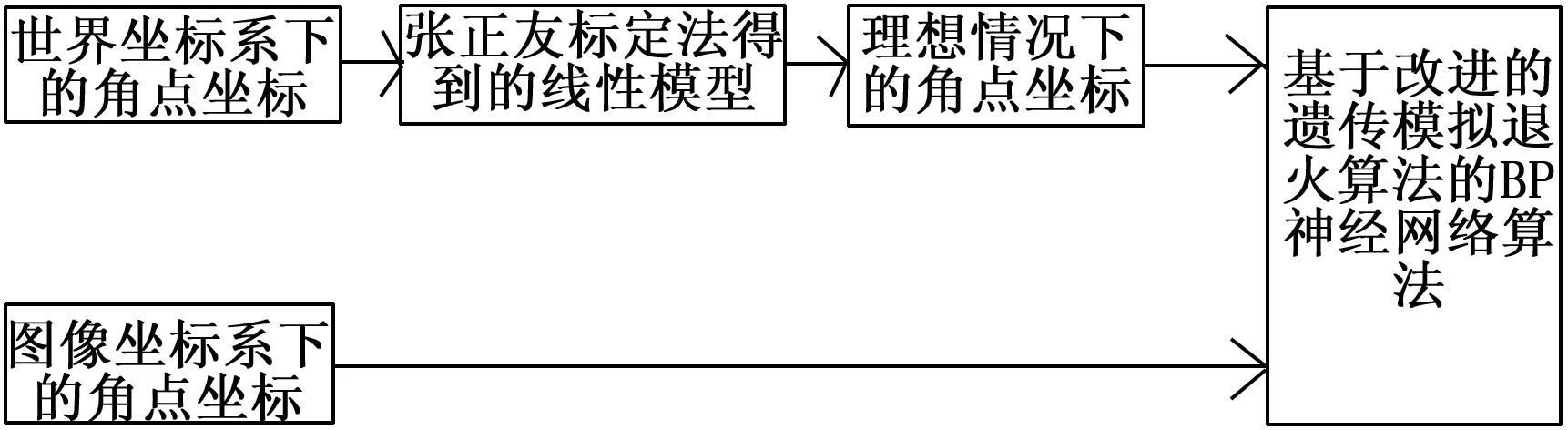
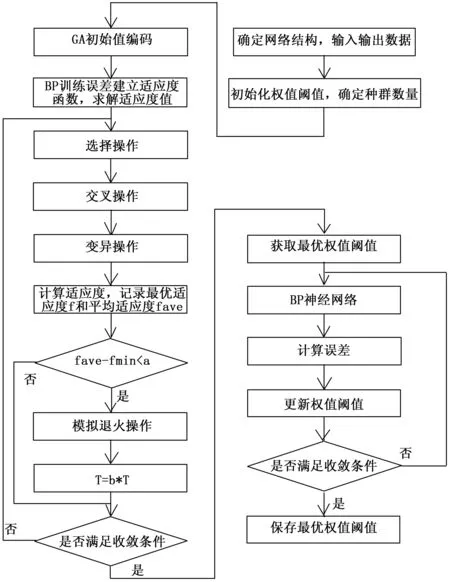
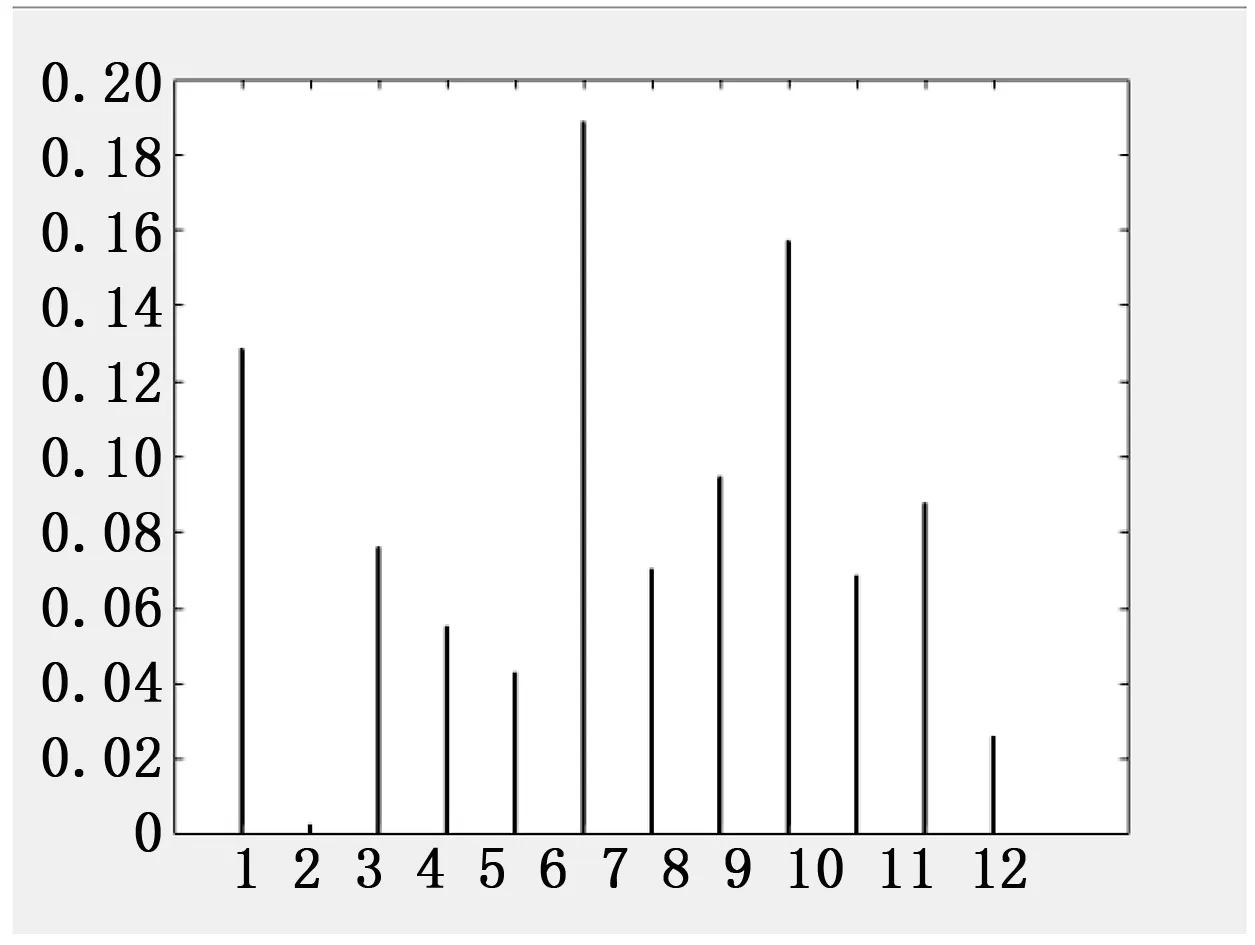
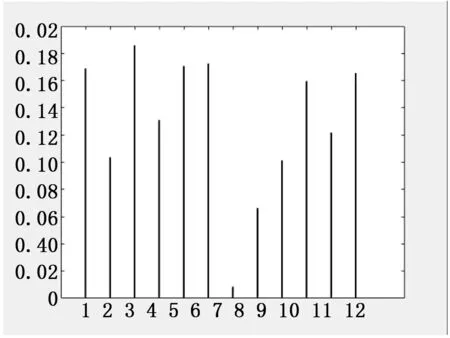
fave-fmin

(10)

其中：fave表示种群中平均适应度值，fmin表示种群中最优个体所对应的适应度值，当平均适应度值接近最优适应度值，即种群进化趋于稳定。

进行模拟退火再优化操作，首先在个体邻域范围内产生新的个体，假设原个体适应度值为f(x)，新个体适应值为f(x′)，新个体取代原个体的概率P如下所示。

(11)

其中：x为原个体，x’为新个体，T为当前模拟退火时的温度。

2.3 基于GA-SA-BP的畸变图像校正算法设计

本文算法对样本进行训练时，基本的流程图如图1所示。

图1 算法的大致流程图

在图1中，无论是理想状态下的角点坐标，还是实际得到的角点坐标都是二维坐标。因此，本文中神经网络模型为2-5-2型，其结构图如图2所示。

图2 神经网络模型架构

在利用改进GA-SA-BP算法对畸变图像进行校正的具体步骤如下：

1)通过张正友标定算法得到相机的内外参数，构建出相机的线性模型，通过角点的世界坐标计算出角点的理想像点坐标，作为网络的输出；通过harris角点检测算法得到角点的实际像点坐标，作为网络的输入；

2)初始化操作。构建BP神经网络架构模型，基于改进的遗传模拟退火算法的初始种群规模N，模拟退火操作的起始的温度T，遗传模拟退火算法中的最大进化代数Gmax，判断种群趋于稳定时的阈值a；

3)根据式(5)计算种群的个体适应度值；

4)利用改进的GA-SA算法来对种群进行操作，得到新的种群；

5)判断当前种群是否趋于稳定，如果趋于稳定，使用模拟退火算法对种群进行操作，然后转步骤6)；如果种群没有趋于稳定，直接转步骤6)；

6)判断当前进化代数是否达到最大进化代数，或者最小适应度值达到所设定的误差精度，如果满足上述条件中的任意一条，则转步骤7)，否则转3)；

7)保存经过改进的遗传模拟退火算法操作后得到的最优的阈值和权值，然后将BP神经网络中的权值和阈值置于最优的权值与阈值，最后通过样本数据来优化网络，得到最终的神经网络模型；

8)利用双三次插值算法对畸变图像进行校正，得到校正后的图像。

改进的遗传模拟退火算法优化BP神经网络的流程图如图3所示。

图3 改进的GA-SA-BP算法流程图

2.4 精度误差结果分析

利用改进的遗传模拟退火算法的BP神经网络算法进行畸变校正，在训练结束后，为了判断训练所得的网络模型是否满足精度要求，往往需要误差分析来判断[14]，误差分析方法采用式(12)，式(13)进行评价。

水平方向的绝对误差为：

Ex=|u-u'|

(12)

垂直方向的绝对误差为：

Ey=|v-v'|

(13)

3 实验结果分析

为了验证在图像畸变校正中本文算法的可行性，在进行仿真实验时，所采用的模板图像为：

图4 模板图像

由图4可知，棋盘格内部有144个角点，其中选取132个特征点用于神经网络的训练，剩下的12个特征点用于对训练所得的网络模型进行测试。

3.1 实验结果

分别采用传统BP神经网络与本文提出的改进的GA-SA-BP算法分别进行实验，所得到的神经网络训练误差曲线图如图5～6所示。

图5 传统BP神经网络训练曲线图

图6 本文算法训练曲线图

从图5，图6中可以看出，用基于梯度下降法的BP神经网络进行训练时，迭代2 000次，最好的误差精度约为，而基于本文算法进行训练时，迭代次数为690次，误差精度为。本文算法较之BP神经网络而言，迭代次数明显降低，提高了效率，同时精度也得以提高。

基于改进的GA-SA-BP算法进行训练，由式(12)，式(13)得到12个测试点的水平方向上误差与垂直方向上的误差，所得的误差结果图如下所示：

从图7，图8，表1可知，本文算法得到的网络模型，用测试样本测试后，水平方向的最大绝对误差为0.188 6像素，垂直方向最大绝对误差为0.185 6像素，12个测试点的RMS值大部分都小于0.1像素，因此本文算法在畸变校正上具有较高的精度。

3.2 畸变图像校正实验

下面利用基于本文算法对SR300相机所采集的畸变图像进行校正，通过双三次插值算法得到校正后的图像。

图7 水平方向的绝对误差图

图8 垂直方向的绝对误差图

测试点的结果如表1所示。

表1 图像的仿真结果

图9 畸变图像

图10 校正后的图像

由图10可看出，畸变图像校正后效果较之畸变图像相比，得到了很好的改善，因此本算法可以用于图像的畸变校正。

基于一般针孔相机拍摄采集得到的图像(图11)，使用本文算法对其进行校正，得到校正图如图12所示。

图11 畸变图像

图12 校正后的图像

利用本文算法对不同两个相机所采集的数据集进行畸变校正，由两组实验结果可看出，校正效果较好。

4 结论

本文采用基于改进的GA-SA-BP算法对图像进行畸变校正，既具有GA算法的全局搜索能力，也具有BP算法较强的局部优化能力，同时在遗传算法中加入模拟退火算法的目的是为了弥补遗传算法易收敛于局部最优的不足，提高了精度。本文算法与传统畸变校正方法相比，无需建立畸变模型，操作简单。最后通过实验分析，结果表明基于改进的GA-SA-BP算法对畸变图像进行校正，校正效果较好，同时将该算法与传统的BP神经网络算法相比，校正精度提高了不少，同时大大降低了迭代次数，提高了效率。