平面向量最值问题的常见解题策略

☉江苏省常熟中学 李一舟

☉江苏省常熟市浒浦高级中学 殷伟康

平面向量最值问题是高考热点问题之一，是架起平面几何图形与坐标系下代数运算的枢纽，备受命题者的青睐.此类问题的特点是试题短小精悍，结构简洁，而且试题新意不断，亮点频出，平实中显精巧雅致，解题入口宽，解法灵活，蕴含着数形结合、化归与转化等数学思想.本文以近几年江苏省市级统考试题为例，对平面向量最值问题的常见解题策略进行归类剖析.

一、合理建立坐标系，将向量最值问题转化为函数最值问题

在解决一些平面图形（如正方形、矩形、直角三角形、等边三角形或直角梯形等）中的向量最值问题时，依据图形的几何特征，通过建立平面直角坐标系，将向量问题坐标化，使研究对象具有简洁的代数表达式，将向量最值问题转化为函数的最值问题.向量坐标法简洁、流畅.

例1（2018年南通市高三第一学期期末）如图1，已知矩形ABCD的边长AB=2，AD=1.点P，Q分别在边BC，CD上，且∠PAQ=45°，则的最小值为______.

解法1：建立如图1所示的直角坐标系，则B（2，0），C（2，1），D（0，1）.

设Q（x，1），P（2，y）（0≤x≤2，0≤y≤1）.

图1

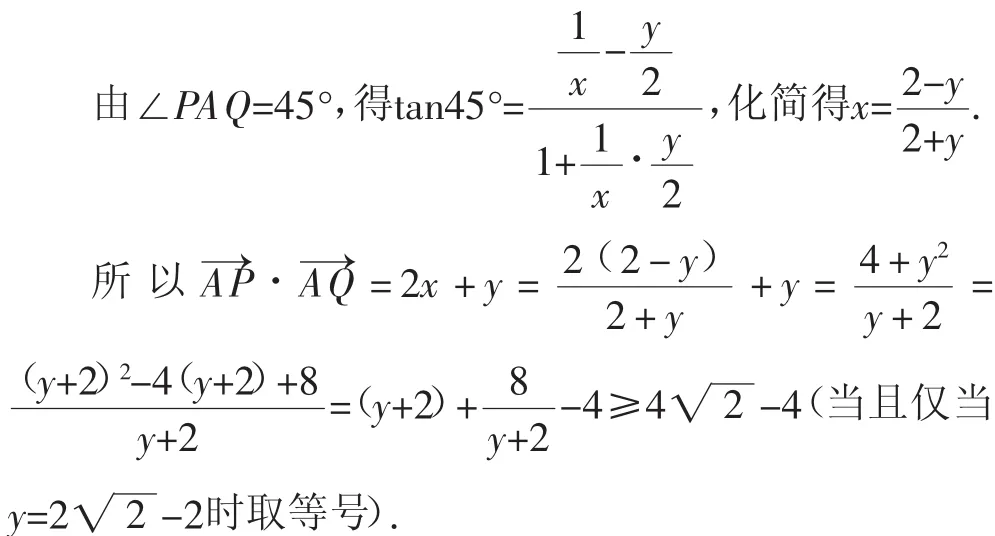
解法2：以A为坐标原点，AB为x轴，AD为y轴建立平面直角坐标系，则A（0，0），B（2，0），D（0，1）.

评注：根据矩形ABCD的特征，建立直角坐标系，解法1是设出Q（x，1），P（2，y），利用条件“∠PAQ=45°”，寻找x与y的关系，将的最小值转化为求解“（y+2）+”的最小值.解法2是通过设∠PAB=θ，用θ表示点P、Q的坐标， 将的最小值转化为求解2tanθ-2”的最小值.

例2（2018-2019学年第一学期苏州市高三数学期中调研测试）如图2，在平面四边形ABCD中，AB⊥BC，AD⊥CD，∠BCD=60°，CB=CD=若点M为边BC上的动点，则的最小值为______.

图2

图3

解析：根据图形，适当调整图形的位置，以点B为原点，BA所在直线为x轴，BC所在直线为y轴，建立如图3所示的平面直角坐标系，则△BCD为等边三角形，且CB=CD=，易得.又∠xAD=60°，所以所以直线令y=0，则x=2，所以A（2，0）.设M（0，t）

评注：根据图形的特征，变换角度，重新设置图形（便于三角形的顶点用坐标表示），如图3，以点B为原点，BA所在直线为x轴，建立直角坐标系，将向量数量积问题转化为函数的最值问题.

二、利用平面向量基本定理，将向量最值问题转化为函数的最值问题

在求解向量最值问题时，合理选择基底，将待求的向量用基底表示，然后利用平面向量基本定理（平面内任何向量都可以用不共线的两个向量线性表示）和向量的线性运算，将原问题转化为函数的值域（最值）问题.

例3（2017年南通市高考模拟试题）在平行四边形ABCD中，，边AB、AD的长分别为2、1，若M、N分别是边BC、CD上的点，且满足最大值为______.

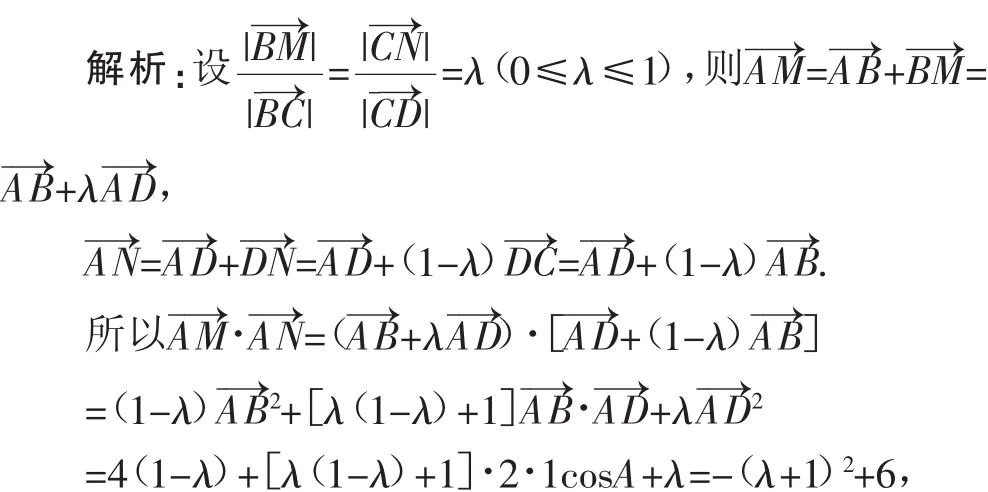
设h（λ）=-（λ+1）2+6，则h（λ）在［0，1］上单调递减，所以当λ=0时，h（λ）max=5，即的最大值为5.故填5.

三、利用平面向量的几何意义，构造几何图形解决向量最值问题

根据平面向量的几何意义，挖掘向量问题的几何背景，构造图形（三角形、平行四边形、圆等），利用数形结合思想进行求解.运用图形意识，将向量最值问题置于适当的几何背景之中，使各种数量关系在图形中简单明了，从而使抽象的向量问题直观化，实现快速解题的目的.灵活掌握向量之间的图形建构，展示了数形结合思想的魅力.

例4（2016·苏北四市三模）已知a，b，c是同一平面内的三个向量，其中a，b是互相垂直的单位向量，且（a-，则|c|的最大值为______.

解析：建立平面直角坐标系，令a=（1，0），b=（0，1），设c=（x，y），则a-c=（1-x，-y），

例5（2018年扬州市高三第一学期期末）已知正三角形ABC的边长为2，点P为线段AB中垂线上任意一点，Q为射线AP上一点，且满足|的最大值为______.

解析：建立如图4所示的直角坐标系，则A（-1，0），C（0，

图4

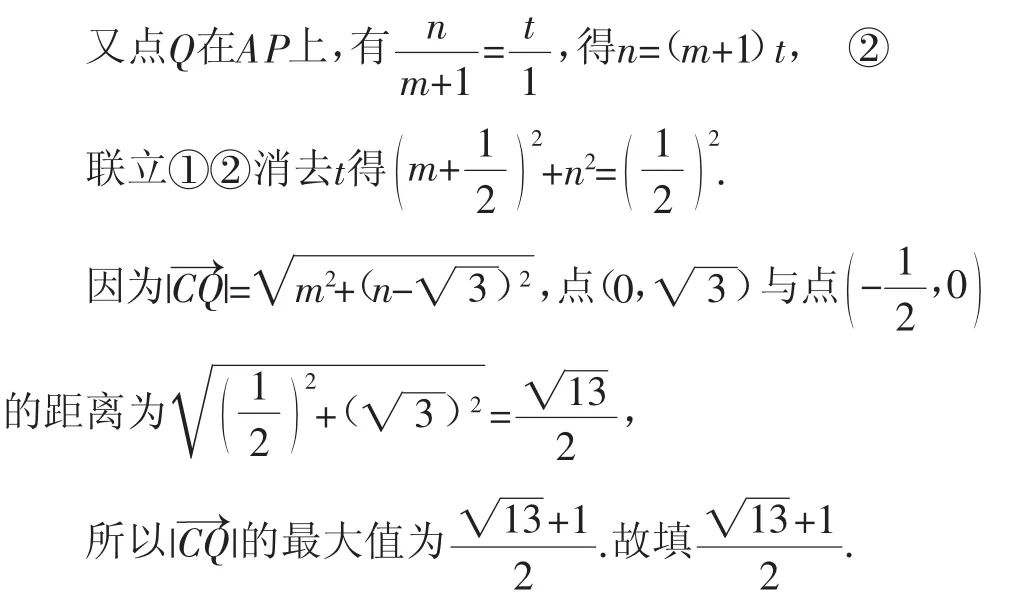
评注：此题求解过程让人有一种“看似寻常却崎岖，成如容易最艰辛”的感觉，究其原因，不知“如何合理引进参数、消参，求出Q的轨迹”.根据图形特征建立平面直角坐标系，将向量最值问题转化为几何问题，目标是求出点Q的轨迹.设Q（m，n），P（0，t），从条件发，得到m+nt=0 ①后，不少人感到束手无策，也有人直接利用点到直线的距离公式求解，然而却无功而返.若能结合“Q为射线AP上一点”这一条件，则，所以n=（m+1）t ②.再由①②消去参数t，则可以求出Q的轨迹方程（即圆M的方程），因此将原问题转化为圆M上的点Q到定点C的最大距离问题.

四、引进适当的参数，利用三角函数的有界性求解向量最值问题

在解决向量最值问题时，引入适当的参数，是为向量最值问题的顺利解决铺路搭桥的一种思维方式.适当地建立坐标系和引入参数，可以使所要研究的向量有简洁的三角函数表达式，将图形的性质与特征赋予代数运算，将向量最值问题转化为三角函数最值问题.

例6（2015年南通市三模）如图5，已知正方形ABCD的边长为2，点E为AB的中点.以A为圆心，AE为半径，作弧交AD于点F.若P为劣弧的最小值为______.

图5

解析：如图5所示，以A为原点，边AB所在的直线为x轴，边AD所在的直线为y轴，建立平面坐标系.设P（cosθ，sinθ），其中D（0，2），C（2，2），所以（-cosθ，2-sinθ）=（2-cosθ）·（-cosθ）+（2-sinθ）2=5-的最小值为

评注：通过建立直角坐标系，引入角参数，利用向量坐标巧妙地将圆的参数方程与三角函数的相关知识连成的最小值转化为三角函数的最小值问题.

五、运用极化恒等式探求向量数量积的最值问题

图6

极化恒等式的几何意义：如图6，在△ABC中，D是BC的中点，化恒等式沟通了向量的数量积与向量线性运算的关系，将不可度量的向量的数量积关系转化为可度量、可计算的数量关系.把向量的数量积用形象的几何图形展示得淋漓尽致，实现了向量与几何、代数三者的有机结合.运用极化恒等式求解数量积的最值问题，可以获得快速、简捷的解法.

例7（2016年南通市二模）如图7，在同一平面内，点A位于两平行直线m，n的同侧，且A到m，n的距离分别为1，3.点B，C分别在m，n上的最大值是______.

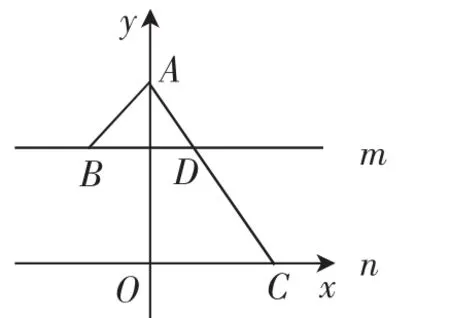
图7

解法1：（坐标法）建立坐标系，如图7所示，则A（0，3）.

解法2：（极化恒等式）如图8所示，连接BC，取BC的中点D，则

图8

评注：运用极化恒等式，把二元变量最值问题转化为一元变量最值问题，运用数形结合思想与平面几何知识确定一元变量的取值范围，可使原问题简捷求解.坐标法与极化恒等式两种方法比较，极化恒等式的处理方式更简洁.此题还有其他解法，但是运用极化恒等式的解法是最简捷、最能体现问题实质的.

平面向量最值问题具有综合性强、灵活性大等特点，其难点是解题方向不明确，往往感到无从下手.因此，解决平面向量最值问题的关键是：合理运用以上五种常见解题策略，善于运用数形结合、化归与转化等思想方法，选择恰当的解题方法，可将复杂问题简单化、抽象问题具体化，从而快捷获解.