从试卷讲评谈数学素养的提高
2019-05-25浙江省慈溪市周巷中学史建波
☉浙江省慈溪市周巷中学 史建波
试卷讲评与平时练习讲评不同,不仅要讲通性通法,也要讲巧法妙法,尤其要讲方法的对比,还要讲做题的心理变化.本文与大家分享在试卷讲评时对一道解圆锥曲线为背景的定点问题的处理.
下面是笔者所在学校的一道高三期末题:
例1已知椭圆离心率为.过椭圆右顶点A的两条斜率乘积为-的直线分别交椭圆C于M,N两点.
(1)求椭圆C的标准方程;
(2)直线MN是否过定点D?若过定点D,求出点D的坐标;若不过,请说明理由.
笔者认为,在试卷讲评时,不要一上来就自己滔滔不绝的讲,因为教师最大的成功不是在于自己有多厉害,而是要看我们培养出的学生有多厉害.试卷讲评课,开始时要“秀”学生,让学生尽情的展示,之后再由教师从如下几个视角进行补充.
(1)对学生讲解的缺陷之处进行补充;(2)对学生讲解的精彩之处进行鼓励;(3)对不同的方法引导学生进行对比;(4)对学生遇到困难的原因进行分析;(5)对学习方法进行适时指导.
一、探究解题方法
通过学生之间的相互交流探索及笔者补充,最后给出该题的如下三种解题思路.
思路1:设出直线AM的方程(斜率为k),与椭圆方程联立,利用根与系数的关系得出点M的坐标.将直线AN的斜率用代换,得出点N的坐标,从而表示出MN的直线方程,得出定点.
思路2:设点表示出AM,AN的斜率.设出直线MN的方程,将直线MN的方程与椭圆方程联立,利用根与系数的关系表示出x1+x2,x1x2,结合AM,AN的斜率之积为-得出直线所过定点.
思路3:利用先定后证的原则,选取特殊情况,如kAM=求出定点,再进行一般性的证明.
明确解题方向后,笔者让两位学生上台板演前两种方法的具体解析过程.第三种方法留给学生课下完成.这样做有利于学生克服对答案的依赖性,提高学生动手解决问题的能力,加深学生对题目的理解.
生1:由(1)可知椭圆右顶点A(2,0).
由题意可知,直线AM和直线AN的斜率存在且不为0.
设直线AM的方程为y=k(x-2).
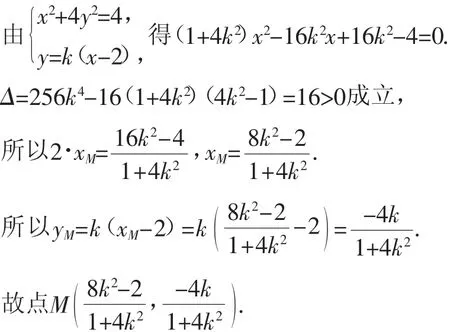

当xM≠xN时,即直线MN的方程为
当xM=xN,即,直线MN显然过定点D(0,0).
综上所述,直线MN过定点D(0,0).
生2:当直线MN的斜率存在时,设MN:y=kx+b,M(x1,

即8b2+16kb=0,解得b=0,或b=-2k(不符合题意,舍去),故直线MN过原点.
综上所述,直线MN过定点D(0,0).
二、类比探究
在得出问题的解法后,笔者引导学生将斜率积改为和,对问题的一般性结论进行探究.
结论:P=1(a>b>0)上一定点,A,B是C上异于点P的两点,直线PA,PB的斜率kPA,kPB满足kPA+kPB=λ(λ为常数,且λ≠0),则直线AB过定点
证明留给学生课下完成.
三、变换探究
例2已知椭圆a>b>0)的离心率,短轴的一个端点到右焦点的距离为2.
(1)试求椭圆M的方程;

当Δ=b2-4(b2-3)>0,即|b|<2时,直线l与椭圆有两个交点.

所以k1+k2为定值.
综上所述,对于一道题目,要从多个角度进行思考,反复琢磨,每种想法都要进行到底,而不是遇到一点困难就马上放弃.如果学生能够从以上三个角度都进行完整的思考,那么就对求解定点问题进行了一次非常高质量的复习.无需多个题目,一题足矣,将来再遇到类似的题目,就能游刃有余地解决.研究的过程,就是学生数学素养提高的过程,提高的不仅是对知识与方法的掌握,还有意志品质、学会选择、自我矫正、方案对比、全局掌控、细节处理、经验积累等方面.
