数学求和问题之裂项相消法

□张宇宙

裂项相消法是高中数学解决数列求和问题的重要方法，是将数列中的每项（通项）分解，然后重新组合，使之能消去一些项，最终达到求和的目的。我以裂项法为例，教授学生从定义中发掘数学方法并向学生揭示方法得来的思维过程。

我们来看一下，本节课本中讲授的是等差数列的前n项的和，而本题目给出的数列的通项公式显然不符合等差数列的通项，但是既然把本题作为等差数列的课后练习题，那么an跟等差数列又有什么联系呢？

我提出本问题，学生经过探讨，普遍给出以下思路：本数列是等差数列的倒数的差，从等差等比的定义得知，等差等比数列实质是研究任一项与前一项的差的一种运算，当然除法也算作减法的一种高级运算，从而揭示出数列定义的本质就是在研究数列的差运算。进而我们在研究数列的时候会研究数列的很多性质，就是我们教学中会给学生总结出的性质，同时我们还会研究数列之间的运算，譬如等差加减等差、等差乘除等差、等差的倒数之差、等比加减等比、等比乘除等比、等比的倒数之比、等差加减等比、等差乘除等比等，都是我们在教学过程中重点研究的，在教学时也建议学生把等差等比数列的所有可能的运算形式尽可能地多尝试一些。

通过学生的这种思路发现，学生能从学过的等差数列发现本数列跟等差数列的一些联系，本数列的通项公式是由等差数列经过取倒数再作差变形得来的，可以看成是一个等差数列的倒数的相邻两项的差的形式，从而我们可以根据它的变形把数列的通项改变成某个数列的相邻两项的差的形式，，所以，在求类似数列的前n项和时，把每一项都改造成某种差的形式，每一项都变成了一种差的组合形式，相邻两项之间就可以部分抵消了，形如：类似地，我们可以求出通项公式为的数列前n项的和。

这种方法是怎样的思维过程得来的呢？我在讲授等差数列求和时，书上给的是高斯求和的方法，我们也称为倒序相加法，那么倒序相加法和裂项相加法之间有什么联系吗？我们再看一下书上给的形式，由高斯算法的启示，对于公差为d的等差数列：

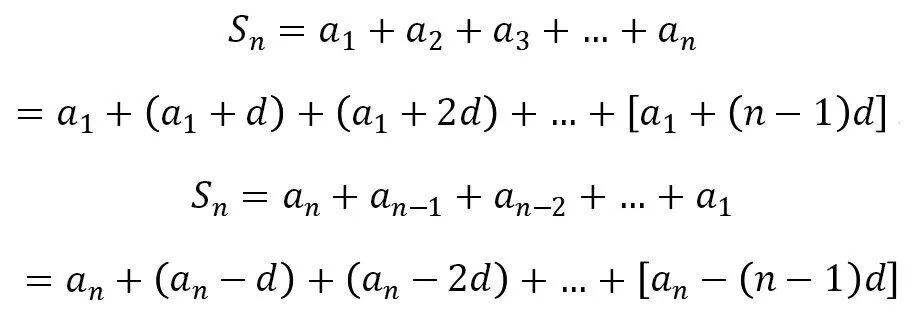
我们发现，书上给的是一种拆分的形式，其实也就是裂项的形式，把a2，a3，…an的每一项都用另一种形式表达，在求和的时候，相邻项之间就可以部分抵消了。这时学生会发现，书上只是用一种易于接受的熟悉的高斯求和法，让学生认识裂项的模样，从而引入裂项相消的方法求和，通过一种学生熟悉的情景带入新的知识方法，这是多么高明的一种引入方法啊。

再回头看书本课后练习的裂项法启蒙题目，如果我们在讲课时只是单纯告诉学生类似于这种形式的数列求和可以用一种很巧妙的方法，叫做裂项法来求解，介绍裂项法解决这种题目是多么巧妙，即使把所有的裂项法的题目类型都给总结一遍，学生如果不能明白其中的来龙去脉，也很难以留下深刻的印象。

在笔者多年的高三教学中发现，很多学生对裂项法掌握得并不好,尤其是去年天津高考理科数学的数列题目就考的裂项法,很多学生的反馈是，知道需要用裂项法求解，但是到底怎么裂就不会了，到底是什么原因导致的呢?就是学生只知道这个方法，但是这个方法到底揭示了事物怎样的本质和联系却没搞清楚。

书上对于高斯法求前n项和这个例题不单纯是为了讲解等差数列的求和，也是给学生展示裂项的一种表达方式，帮助学生能很好地理解裂项法的来龙去脉。平常教学中，教师要多讲解方法的来龙去脉比单纯让学生把方法背下来反复练习要好。例如，等比数列的求和，书上给的是错位相减法，其实仍然可以用裂项法给出，很多学生通过自己提前预习课本，对于错位相减法很熟悉，如果我们再在上课时把错位相减法重复多遍，学生容易不感兴趣，让学生自己去探讨，去发现，去用书上没有的方法解决书上的数学问题，会使学生学习数学的积极性大幅提高。

再进一步，揭示了裂项法的来源之后，我们能不能找到一个有关裂项法的万能公式呢？我们发现，，分母可以看成一个数列的相邻两项的乘积，分子恰好是这相邻两项的差，即，这种形式在以前的数学学习中都是从右端开始做起，得到左端的结果，也就是通分，在这里是通分的逆用，即，这个规律我们在裂项题目中都会发现，符合此规律的通项公式也就可以用裂项法求和，例如：都可以用类似思路解答，其中

然后就可以在求和时进行相邻项之间的抵消求和了。

本文通过讲述裂项法问题，启发学生学会从定义、实际问题中发掘数学方法，并学会揭示方法得来的思维过程。把思维过程表述成语言表达或者数学符合表达的形式就是数学规律，用我们发现的数学规律就可以解决更多的类似的问题，一个完整的数学探索过程也就完成了。