一类对角互补型问题的解题策略
2019-05-25范建兵
范建兵
笔者偶遇一道常州中考数学填空压轴题,思绪万千,不禁为其精心的构思、模型化的考查拍手叫好。
【原题呈现】如图1,在⊙O的内接四边形ABCD中,AB=3,AD=5,∠BAD=60°,点C为弧BD的中点,则AC的长是 。

图1
【解析】由题意知,BC=CD,∠CAD=∠CAB=30°,∠BAD+∠BCD=180°,∠B+∠D=180°。
解法一:运用旋转策略。
如图2,将△ACD绕点C逆时针旋转120°,得△CBE,则∠E=∠CAD=30°,BE=AD=5,AC=CE,得△ACE是一个顶角为120°的等腰三角形,作CM⊥AE于M,解此三角形可得AC的长。
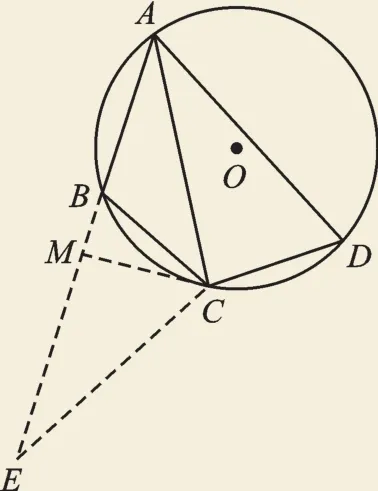
图2
解法二:运用角平分线策略。
如图3,过C作CE⊥AB,交AB延长线于E,CF⊥AD于F,借助角平分线性质、两次三角形全等、30°角特殊性质、勾股定理等知识可得AC的长。

图3
【模型解读】如图4,从原题中四边形ABCD来看,结合“圆内接四边形对角互补”,可得这个四边形属于“对角互补型”四边形。
此类问题解题一般有两个显性特征:(1)有一组相等的邻边,如原题中的BC=CD,旋转后使BC与CD重合;(2)四边形对角互补,如原题中的∠B与∠D,旋转后构造三点共线。
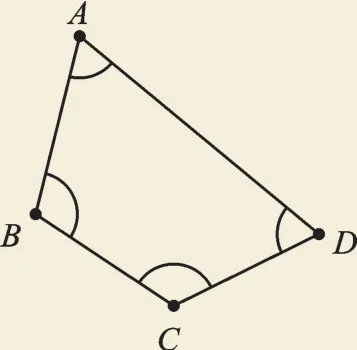
图4
【模型再现】如图5,在四边形ABCD中,AB=AD,∠BAD=∠BCD=90°,连接AC。若AC=6,求四边形ABCD的面积。
这是典型的“对角互补型”问题,与原题相比隐藏了一个四边形ABCD的外接圆,有了上面的理解,解答这样的题目是不是很简单呢?

图5
【点评】“对角互补型”问题的图形中,除了隐圆(四边形四个顶点在同一个圆上)和两个显性特征,还有哪些隐性结论呢?如果我们深度反思,能发现这类问题的“内涵”还是挺丰富的,让我们结合下列图形去探求其中的奥秘。
(1)如图 6,∠AOB=∠DCE=90°,OC 平分∠AOB,你能写出哪些结论?如果将∠DCE绕点C旋转,如图7,这些结论还成立吗?

图6

图7
(2)如图8,∠AOB=2∠DCE=120°,OC平分∠AOB,你能写出哪些结论?如果将∠DCE绕点C旋转,如图9,这些结论还成立吗?
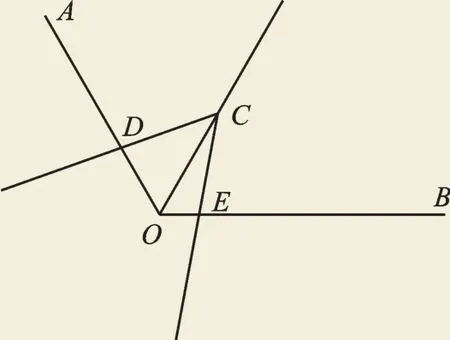
图8

图9
以上两种情况,请同学们自行思考哦。其实解题就如学习,只要认真思考,细细体会,就一定会发现更多的奥秘。
