正方形的“半角模型”

2019-05-25范大阳

初中生世界 2019年19期

关键词：边长勾股定理四边形

范大阳

过正方形任一内角的顶点，在形内引两条射线，使两条射线的夹角是该内角的一半（即45°），像这样的模型，我们习惯称之为正方形的“半角模型”。

【模型讲解】如图1，在正方形ABCD中，点E、F分别为BC、DC边上的点，∠EAF=45°，连接EF，求证：DF+BE=EF。

图1

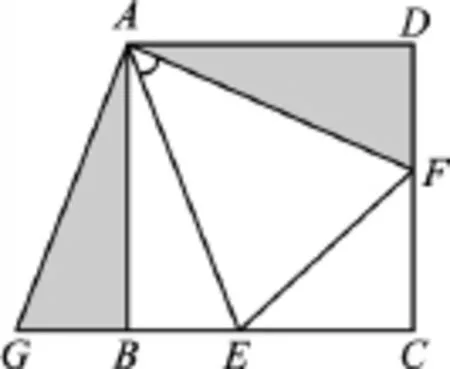
图2

【解析】一般方法是：将45°角两边的三角形旋转到一边，合并成新的三角形，从而进行等量代换，然后证明这个新三角形与半角（45°角）形成的三角形全等，再通过全等的性质得出线段之间的数量关系。

【证明】将△ADF绕A点顺时针旋转90°得到△ABG，如图 2，则 AG=AF，∠GAB=∠DAF，∠ABG=∠ADF=90°，所以∠ABG+∠ABC=180°，所以G、B、C三点共线。再证明△GAE≌△FAE，就可得到EF=GE=GB+BE=DF+BE。

【推论】对于这样的正方形“半角模型”，除了有以上常用结论（①DF+BE=EF）之外，我们还可以推出以下常用结论：②S△AEF=S△ABE+S△ADF；③△AEF中，边EF上的高等于正方形的边长。同学们可以自行推导哦。

【知识运用】例1 如图3所示，在四边形ABCD中，AD∥BC（BC＞AD），∠B=90°，AB=BC=18cm，E是AB上一点，当∠DCE=45°时，BE=6cm，则DE= 。

图3

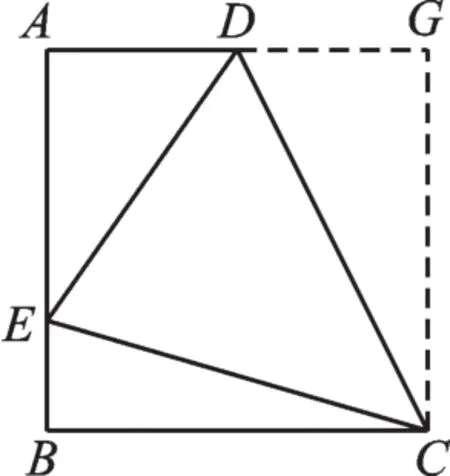
图4

【解析】由∠A=∠B=90°、AB=BC两个条件联想到正方形。其实这是一个“残缺”的正方形，所以只需把被“割去”的那一部分补上就可以了，再结合“∠DCE=45°”，就可以得到正方形的“半角模型”了。

如图4，作CG⊥AD，交AD的延长线于G，先证明四边形ABCG是正方形，再由上述结论①可知 ED=BE+DG，设 DE=x，则 DG=x-6，AD=24-x，由勾股定理得，AE2+AD2=DE2，即 122+（24-x）2=x2，解得x=15，即DE=15cm。

【反思】本题考查的是正方形的判定和性质、勾股定理的应用，“补全”正方形是解题的关键。

【变式】在例1中，如果AB=BC=18cm，AD=9cm，那么△CDE的面积= 。

【解析】如图4，可设BE=x，则DE=BE+DG=x+9，AE=18-x，在Rt△AED中，利用勾股定理便可求出x=6，则DE=15，利用上述结论③可以得知△CDE中边DE上的高等于正方形边长18，或者利用上述结论②也可以求出△CDE面积。答案：135cm2。

例2 如图5，在矩形ABCD中，AB=2，BC=4，点E、F分别在BC、CD上，若AE=5，∠EAF=45°，则AF的长为。

【解析】本题属于“残缺型”半角模型，因为里面有个45°角，所以我们不难想到把矩形补成正方形。

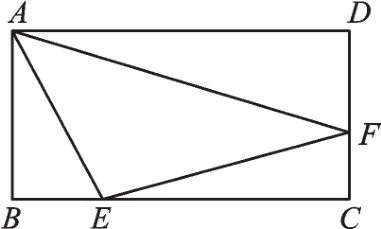
图5

图6

如图6，分别延长AB、DC，使得它们都等于AD，分别得到AG、DH，连接GH，延长AE交GH于I，连接FI，易知四边形AGHD是正方形。在Rt△ABE中，由勾股定理可求出BE=1，∵BE∥GI，∴△ABE∽△AGI，∴，∴GI=2，设DF=x，由正方形“半角模型”结论①可知，FI=DF+GI=x+2，FH=4-x，IH=4-2=2，在Rt△FIH中，由FI2=IH2+FH2得到（2+x）2=（4-x）2+，即DF=，在Rt△ADF中，运用4，解之，得x=勾股定理便可求出AF=

【反思】本题考查了正方形的判定及性质、相似三角形的判断和性质、勾股定理的运用，正确添加辅助线构造正方形的“半角模型”是解题的关键。当然，本题还有其他方法，不过笔者认为，如果熟悉“半角模型”，此法相对而言较容易想到。

例3 如图7，在△ABC中，∠BAC=45°，AD⊥BC，BD=4，CD=6，则△ABC的面积为。

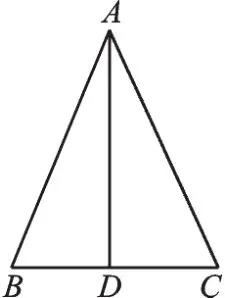
图7

图8

【解析】本题关键就是求出AD，而这里也有个45°角，我们不难想到正方形“半角模型”结论③，而A点又必须成为直角顶点，我们可以把AD进行翻折变换，构造正方形。

如图8，将△ABD沿着AB边折叠，使D与E重合，△ACD沿着AC边折叠，使D与G重合，可得∠BAD=∠EAB，∠DAC=∠GAC，∴∠EAG=∠E=∠G=90°，AE=AD=AG，BD=EB=4，DC=CG=6，∴四边形AEFG为正方形。设正方形的边长为x，则BF=x-4，CF=x-6，在Rt△BCF中，根据勾股定理得：BF2+CF2=BC2，即（x-4）2+（x-6）2=（4+6）2，解得：x=12或x=-2（舍去），∴AD=12，