纠正错题 提高解题能力
2019-05-25韩宝华
韩宝华

“四边形”这一章的性质、定理很多,它与角平分线、全等三角形等知识点相综合,题型丰富。同学们在解决有关四边形问题时,会产生各种错误。希望通过学习本文,同学们能更好地理解题目的本质,提高解题能力。
一、画图不全面,漏解
例1 已知在平行四边形ABCD中,AB=6,∠ABC的平分线BE把边AD分成3∶2的两部分,求这个平行四边形的周长。
【错解】32。
【错因分析】题目中没有给出图形,有些同学在做题画图时没有考虑线段AD的成比例的两部分的两种情况。因此,漏解是解决四边形问题时常会出现的错误。
【正解】如图1,∵四边形ABCD是平行四边形,∴AD∥BC,

图1
∴∠AEB=∠CBE。
∵BE平分∠ABC,
∴∠ABE=∠CBE,
∴∠AEB=∠ABE,
∴AE=AB。
当AE∶ED=3∶2时,可设AE=3x,则ED=2x,AD=5x,AB=AE=3x,
又∵AB=6,∴x=2,∴AD=10。
此时平行四边形的周长为2×(6+10)=32。
当AE∶ED=2∶3时,如图2,可设AE=2x,则ED=3x,AD=5x,AB=AE=2x,

图2
又∵AB=6,∴x=3,∴AD=15,
此时平行四边形的周长为2×(6+15)=42。
【点评】当题中没有给出图形时,大多数情况下要结合题意,正确画出图形。此外,要考虑分类讨论。
二、混淆矩形、菱形的判定定理
例2 如图3,已知四边形ABCD,点E、F、G、H分别是各边的中点。
(1)当AC、BD满足什么条件时,可得四边形EFGH是矩形?
(2)当AC、BD满足什么条件时,可得四边形EFGH是菱形?
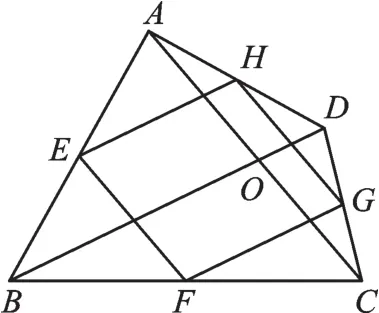
【错解】(1)AC=BD;(2)AC⊥BD。
【错因分析】在得到中点四边形EFGH的基础上,把原四边形ABCD的对角线混淆成四边形EFGH的对角线。
【正解】(1)AC⊥BD。
证明:∵E、F分别是AB、BC的中点,
∴EF∥GH,且EF=GH,
∴四边形EFGH是平行四边形。
若证四边形EFGH是矩形,
证明∠EFG=90°即可。
∵EF∥AC,FG∥BD,
∴只需BD⊥AC即可。
(2)AC=BD。证明可类比(1)。
【点评】类比法不仅是一种从特殊到特殊的推理方法,更是一种寻求解题思路、猜测问题答案或结论的方法。
三、不能将特殊四边形转化为特殊三角形
例3 如图 4,在坐标系中,有A(0,6)、C(8,0),动点P以2个单位/秒的速度从点A沿线段AC向点C移动,同时动点Q以1个单位/秒的速度从点C沿CO向点O移动,当其中一点到达终点时,P、Q同时停止运动。
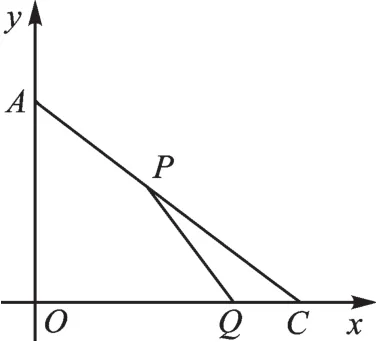
图4
(1)用时间t表示P点坐标。
(2)t为何值时,平面中存在点M,使得以P、Q、C、M为顶点的四边形为菱形。
【错因分析】(1)不能正确地根据线段关系表示线段长,不能构造相似求线段长。
(2)对菱形与等腰三角形的关系理解不透,不能将菱形的存在转化为等腰三角形的存在。
【正解】由题意可得:AP=2t,AC=10,PC=10-2t,CQ=t。
(1)如图5,过点P作PH⊥OC,垂足为点H,则可得△CPH∽△CAO,
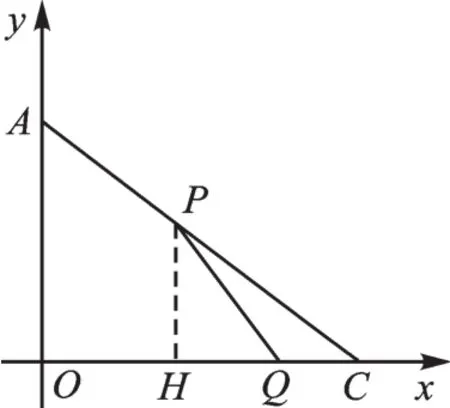
图5
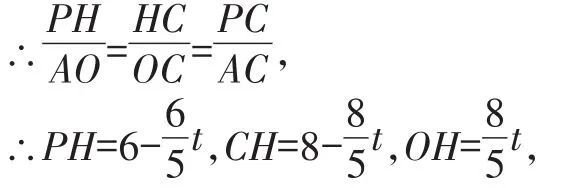
(2)①代数法:如图5,
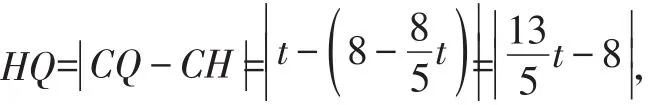
在Rt△PHQ中,PQ2=PH2+HQ2。
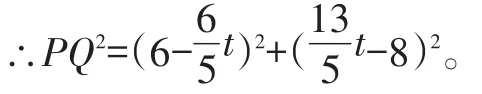
若CQ=CP,存在四边形CQMP为菱形,则:t=10-2t,得t=
若PQ=PC,存在四边形PQMC为菱形,这时 PQ2=PC2,即:(6-)2+(t-8)2=(10-2t)2,得t=
若QP=QC,存在四边形PQCM为菱形,则QP2=QC2,即:(6-t)2+(t-8)2=t2,得t=。
②几何法:若CQ=CP,存在四边形CQMP为菱形,则:t=10-2t,得t=。
若PQ=PC,如图6,存在四边形PQMC为菱形,过点P作PG⊥OC于点G,
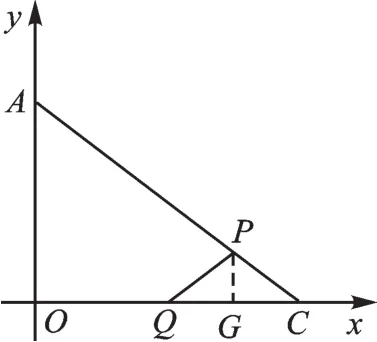
图6
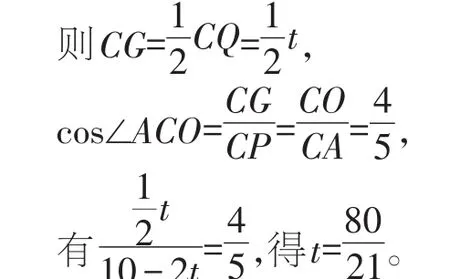
若QP=QC,如图7,存在四边形PQCM为菱形,过点Q作QG⊥AC于点G,
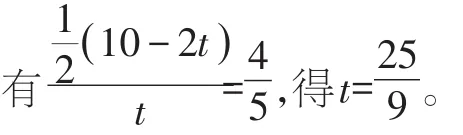
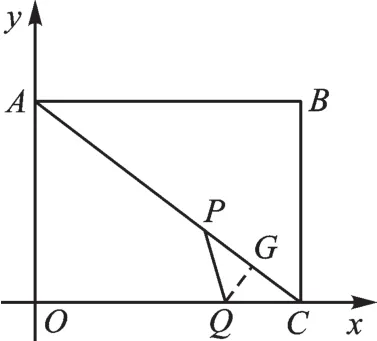
图7
【点评】因为菱形是以对角线所在的直线为对称轴的轴对称图形,故只要△CPQ为等腰三角形,然后沿着△CPQ的底边翻折,可得菱形。
四、解题过程不规范
例4 已知:如图8,在▱ABCD中,AE⊥BD,CF⊥BD,垂足分别为E、F.求证:△ADE≌△CBF.

图8
【错解】∵AE⊥BD,CF⊥BD,
∴∠AED=∠CFB=90°,
∵四边形ABCD是平行四边形,
∴∠ADE=∠CBF,
∴△ADE≌△CBF。
【错解原因】不能直接由平行四边形ABCD得到∠ADE=∠CBF。△ADE≌△CBF还缺等边条件,应该在证明中呈现出来。
【正解】∵AE⊥BD,CF⊥BD,
∴∠AED=∠CFB=90°,
∵四边形ABCD是平行四边形,
∴AD=CB,AD∥BC,
∴∠ADE=∠CBF,
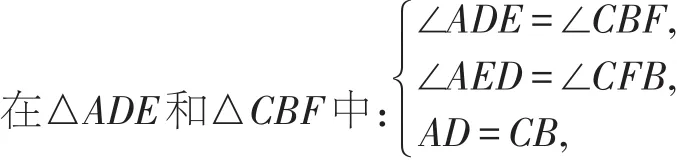
∴△ADE≌△CBF。
同学们,做错题不可怕,只要我们能够找到产生错误的原因,迎难而上,相信自己,一定能提高解题能力。
