具有负反馈机制的改进的蚁群算法在机器人路径规划中的应用

梁娜

(铜川职业技术学院 基础部, 铜川 727031)

0 引言

近些年，随着机器人研究的发展，机器人路径规划也获得一定的进步，越来越多的学者提倡通过多种路径规划算法，例如：遗传算法[1]、粒子群优化法[2]等。但不得不说， 路径规划主要目的始终不变，就是找出一条自起点至目标点之间的最优路径，包含用时及其路径最短，避开一系列的障碍物到达至顶点。蚁群算法作为一种群智能算法，主要用于解决机器人路径规划、集成电路布线等方面的问题。Dorigo等[3]最早提出利用蚁群算法解决旅行商问题。Marzband等[4]提出一种以多层蚁群优化为基础的能量管理系统算法，在实时调度过程中对微源的最佳运行加以明确，以达到节省电力生产成本的目的。孟建东[5]在简要分析计算机网络路由优化方面问题基础上，提出利用蚁群算法解决计算机网络信息传输环境出现的延时抖动、路径消耗大等问题，研究结果表明，所用改进的蚁群算法，有利于避免发生局部最优值的问题。由于蚁群算法存在在一定概率下陷入局部最优解的不足之处，这种情况难以指导机器人寻找最优的路径，只是获取次优解。为有效解决这一问题，本研究引入负反馈机制的改进蚁群算法，用于完成机器人路径规划，仿真结果证实，所使用的改进蚁群算法在复杂问题下获取最短距离，平均距离及最优路径成功率均优于传统算法性能。

1 建立环境模型

本研究使用W.E.Howden提出的栅格法[6]建立环境模型，栅格法是指对模拟的机器人所处环境进行划分，组成大小相同的栅格，采用栅格代表可行驶或者障碍区域。如今，这种方式已经被广泛用于多数机器人系统中，详细描述为：栅格法就是把机器人所工作空间划分为二进制信息网格单元，处在静态环境下，假定障碍物大小、位置为已知条件，且机器人所处二维空间模型用D表示，通过网格对D空间实施均匀的分割[7]。对于网络与不可行驶区域之间的交点，可以划分为可行、不可行网格，前者用白色格子代表，后者以褐色格子表示，绿色、红色分别代表这起点、终点，具体见图1所示。

通过上述分析，利用序号法，遵循自左至右、从上至下这一顺序完成栅格编号操作。每一个栅格均设定所对应的序号及坐标，即：第i行、j列栅格记作：D(i,j)，与之对应的序号是k。而k和(xi,yj)坐标间的关系如式(1)、式(2)所示。

图1 环境建模效果图

(1)

yj=int[(k-1)/Nh]+1

(2)

上述式子中,Nh代表每一行栅格数，mod表示求余计算。必须注意，机器人实际运动中，因其每走一部均是从一个栅格中心进入相邻栅格中心，因此，默认其运动方向设置为8个。

2 蚁群算法及其改进

2.1 概述蚁群算法

(3)

信息素更新主要由会挥发、释放这两个过程组成，在全部蚂蚁完成一次搜索后，利用当前最优路径指导其他蚂蚁搜索路径如式(4)。

(4)

(5)

蚁群算法的程序结构流程示意图，如图2所示。

2.2 算法的不足与改进思想

对于蚁群而言，负反馈即信息素τ的堆积。由公式(15)可知，蚂蚁在随机走完一次循环之后，对于所发现的较短路径，会有较多信息素的遗留。之后通过公式(3)，信息素越多，就会有更高的概率吸引蚂蚁在下一次循环之中选择此路径。如此不停循环，最终，全部的蚂蚁均会选择此路径，蚂蚁群体的范围便会逐渐收敛。但是，蚁群算法在处理大规模问

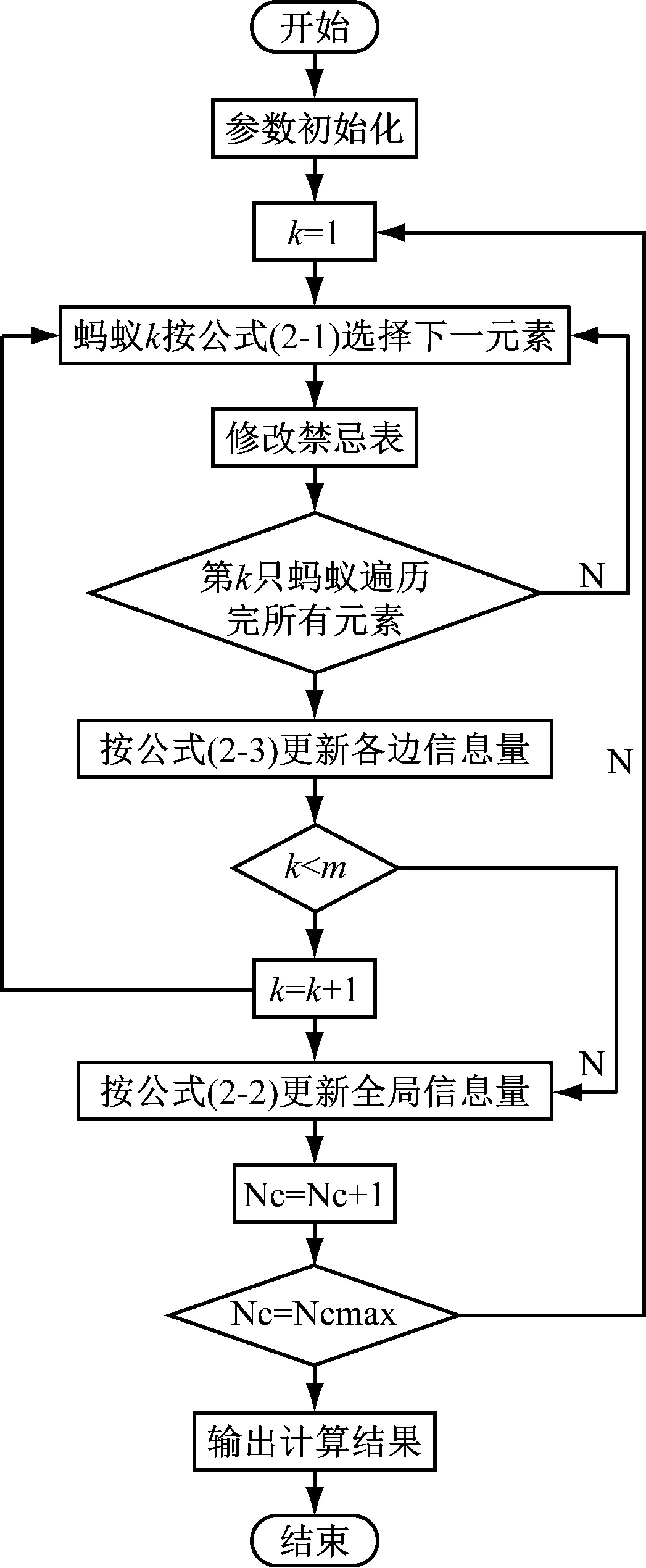
图2 算法流程图

题之时所取得的效果并不理想，究其原因，根本在于负反馈程度是不变的。由此，基于排序蚂蚁算法(ASrank)改进之处在于，不单只是最优路径上的蚂蚁释放信息素，先要对蚂蚁照出的所有路径给予排序处理，随之，挑选路径排序处于前列的蚂蚁释放相应地信息素[9]。蚂蚁依据路径长短完成排序，所释放信息素量根据排序等级做好加权处理。求解为式(6)。

(6)

式(6)中，ω代表每一次迭代处理后路径排序靠前释放相应信息素的蚂蚁总数；Cb代表最优的路径距离；Δτb(i,j)代表当前最优蚂蚁所释放信息素情况；Δτk(i,j)是前(ω-1)只蚂蚁信息素释放状况；Ck为排名处于前列的蚂蚁寻找距离，为式(7)、式(8)。

(7)

(8)

MMAS算法改进点在于，基于AS算法搜索方法与防止早熟收敛机制相结合，促使算法获取最优性能[10],这种算法能对路径上的信息素总量给予有效的控制，使其保持在一定范围之内，防止蚂蚁过快收敛得到局部最优路径，确保蚂蚁可以搜索更为广泛的领域[11]。信息素遵循下列规则更新为式(9)。

(9)

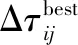
(10)

2.3 具有负反馈机制的改进的蚁群算法

在蚁群算法用在处理复杂环境下，蚂蚁会倾向于挑选简单路径，导致算法极易进入局部最优解局面，从而错过最优的路径。针对上述情况，文中提出具备负反馈机制改进的蚁群算法(AS-N)有效解决这一问题，并由路径构建及信息素更新两个方面实施优化改进。在增加负反馈机制的蚁群算法内，某一信息素可利用正(τij)、负(φij)反馈信息素矩阵代表。首先，对正、负反馈信息矩阵进行初始化处理，寻优环节通过历次迭代最优方法实时更新信息素。路径实施搜索环节，不仅要存储最佳路径，也必须将最差路径保存下来[12]。信息素更新过程中，不单要在最优路径方面释放正反馈信息素，且在最差路径方面将负反馈信息素释放出来。在建立路径时，通过式(11)为下一步移动进行指导。

(11)

式(11)中，δ表示较差路径上设定的负反馈信息素上界，a、y代表正、负面反馈信息矩阵，β表示启发式信息权重值。与原来的算法比较，在新公式内引入惩罚项δ-φij(t)。由于迭代次数不断增加，在并未探索的路径上δ-φij(t)明显比恶化路径上的数值大。基于此，运用这个新公式挑选路径，并把蚂蚁引导至未知路径内。此时，资源总量处于一定的状态，因此，必须充分运用有限资源，促使蚂蚁更少并探索新的恶化路径，有更多蚂蚁取搜索未知路径，防止陷入局部最优的解中。其中，使用最短、长路径及时更新正、反馈信息素，为式(12)～式(15)。

(12)

(13)

(14)

(15)

3 实验分析

3.1 设置合理的参数

本次实验中，选取AS、MMAS、ASrank及AS-N算法进行对比分析，并设定在复杂及简单环境下具体结果。经过改进处理的蚁群算法主要包含a、β、ρ、γ、δ以及蚂蚁数量等参数，其中，信息素a在限定的范围之内[1,5]，进行实验中设置为2；蒸发速率ρ处在[0.01,0.03]范围之内，实验取值为0.02；蚂蚁能见度β处在[5，12]范围内，实验数据设定为8；负反馈信息素因子γ、δ限定范围为[1，5]、[5，15]实验使用的数据为γ=2，δ=10。

建模环境设计如下：设置不同复杂度的40*40网格工作区，起点、目标点未知依次为(1，1)、(40，40)，每一个小网格长度设定1cm。最大迭代次数是25次，种群大小是100，在不同的复杂障碍条件下仿真结果如图3所示。

3.2 简单问题结果分析

从简单问题视角来说，挑选30组数据对比算法的优越性，并给出不同的算法寻找最优结果平均距离及其运行时间，详细如表1所示。

根据所选4种算法实验结果可知，因所分析问题比较简单，改进一群算法性能提高并不显著。

此外，处在简单环境状态下，选取30组数据平均值，分析其收敛状况，如图4所示。

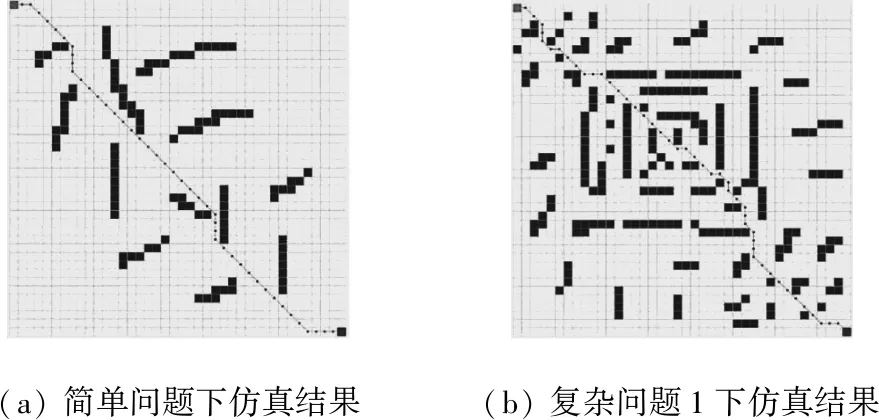
(a) 简单问题下仿真结果(b) 复杂问题1下仿真结果

(c) 复杂问题2下仿真结果(d) 复杂问题3下仿真分析

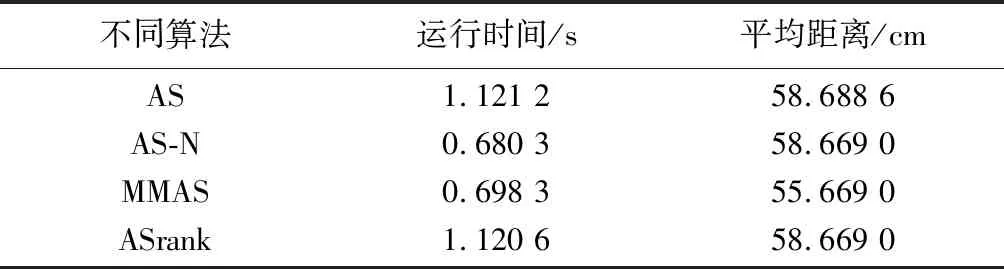
图3 不同复杂障碍条件下仿真结果示意图

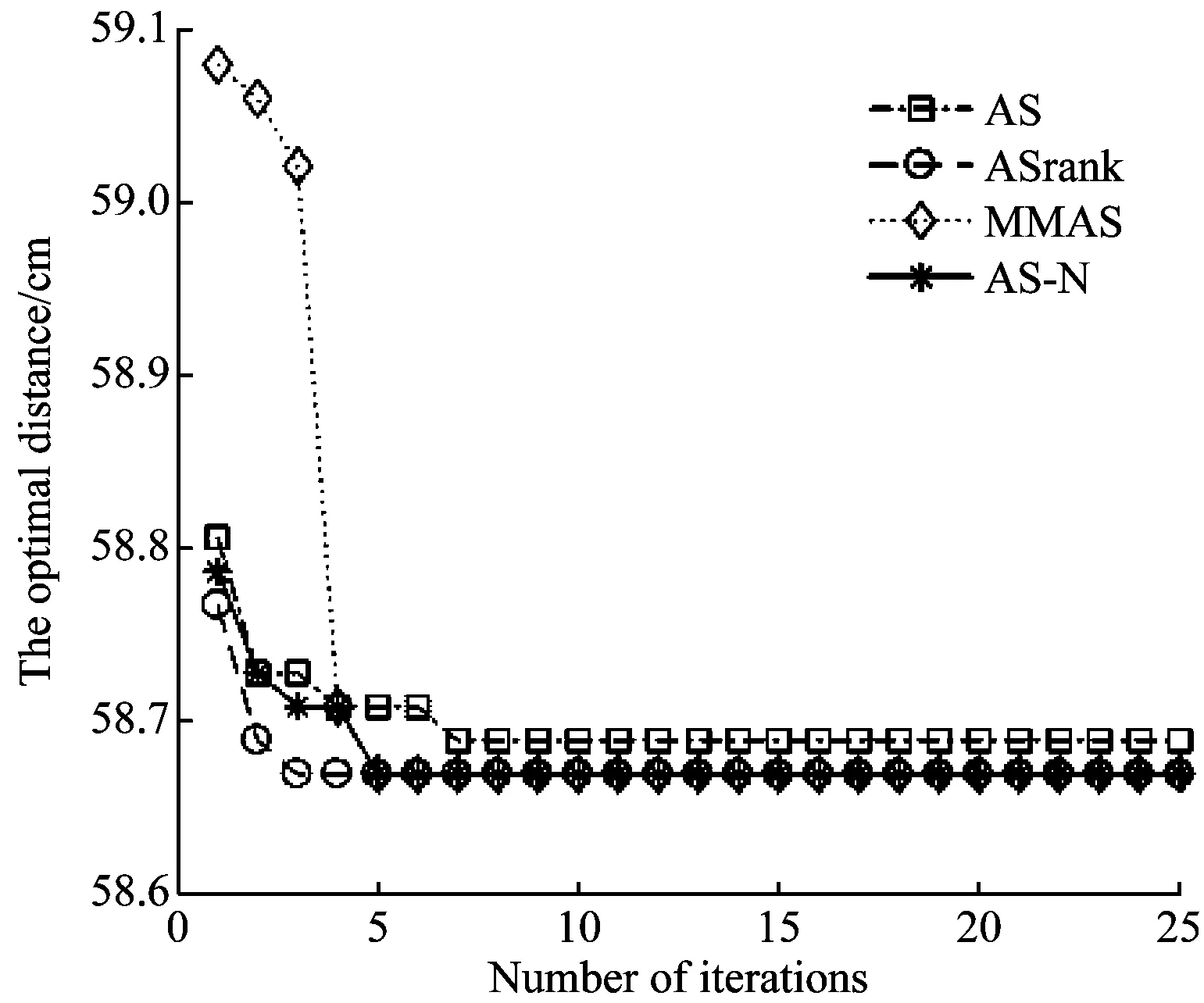
图4 简单条件下不同算法收敛状况对比

分析下图及上表数据可知，这4种算法之间的差距并不显著，这是因为所用改进算法能够轻松解决简单条件下路径规划问题。

3.3 复杂问题分析

对1-3这三个复杂问题来分析，依次挑选30组数据对比所用算法的优越性。不同复杂障碍状态下所用算法寻优平均运行时间及距离,如表2所示。

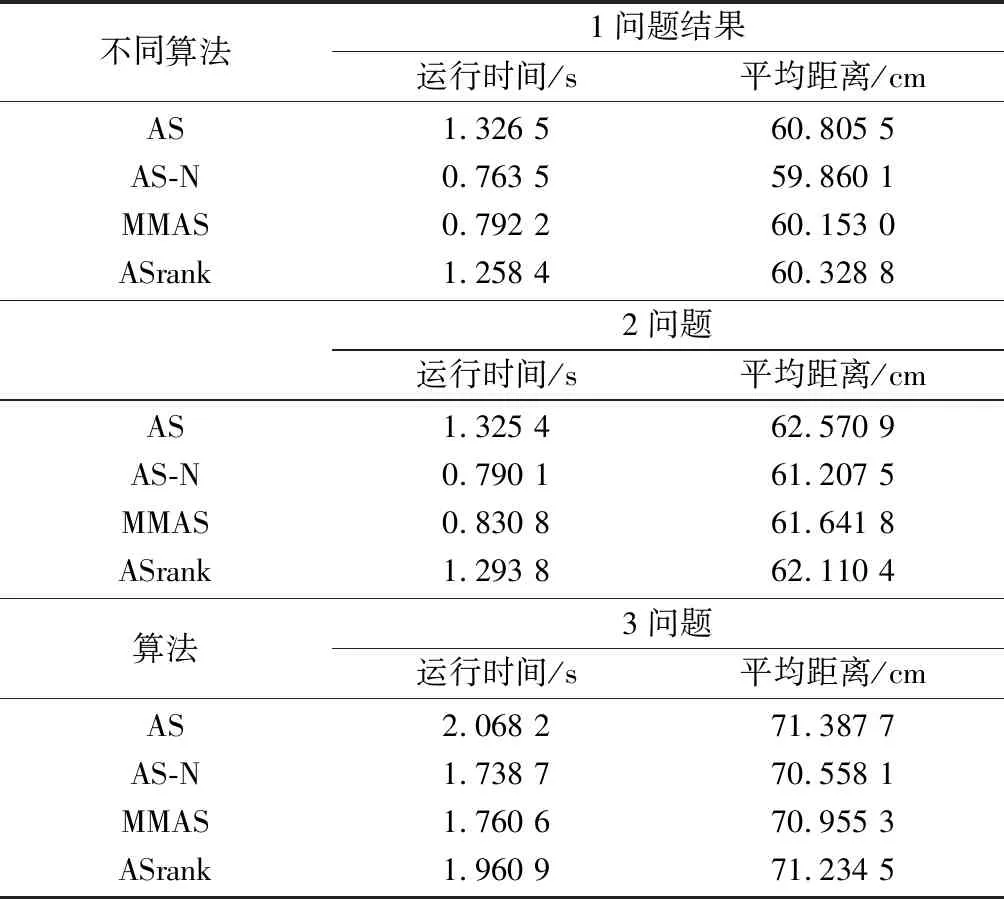
表2 各种复杂问题寻优距离及运行时间结果分析

因问题复杂程度增加，改进AS-N算法优越性更显著，不管是在运行时间或者寻优距离方面，这种算法均能获取良好的效果。

在1-3这三个复杂问题环境下，依次选取30组数据平均值，分析所用4种算法收敛状况，如图5所示。与简单环境相比较，根据该收敛图可知，AS-N算法展现出良好的优越性，说明这种算法能在复杂环境下稳定的寻找最优路径。

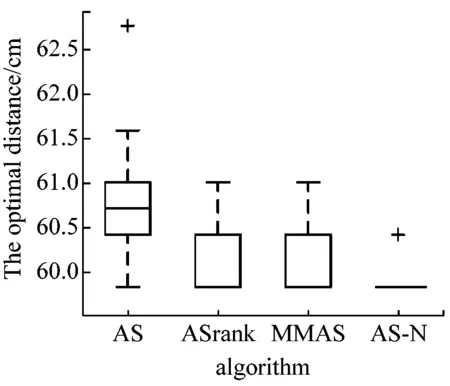
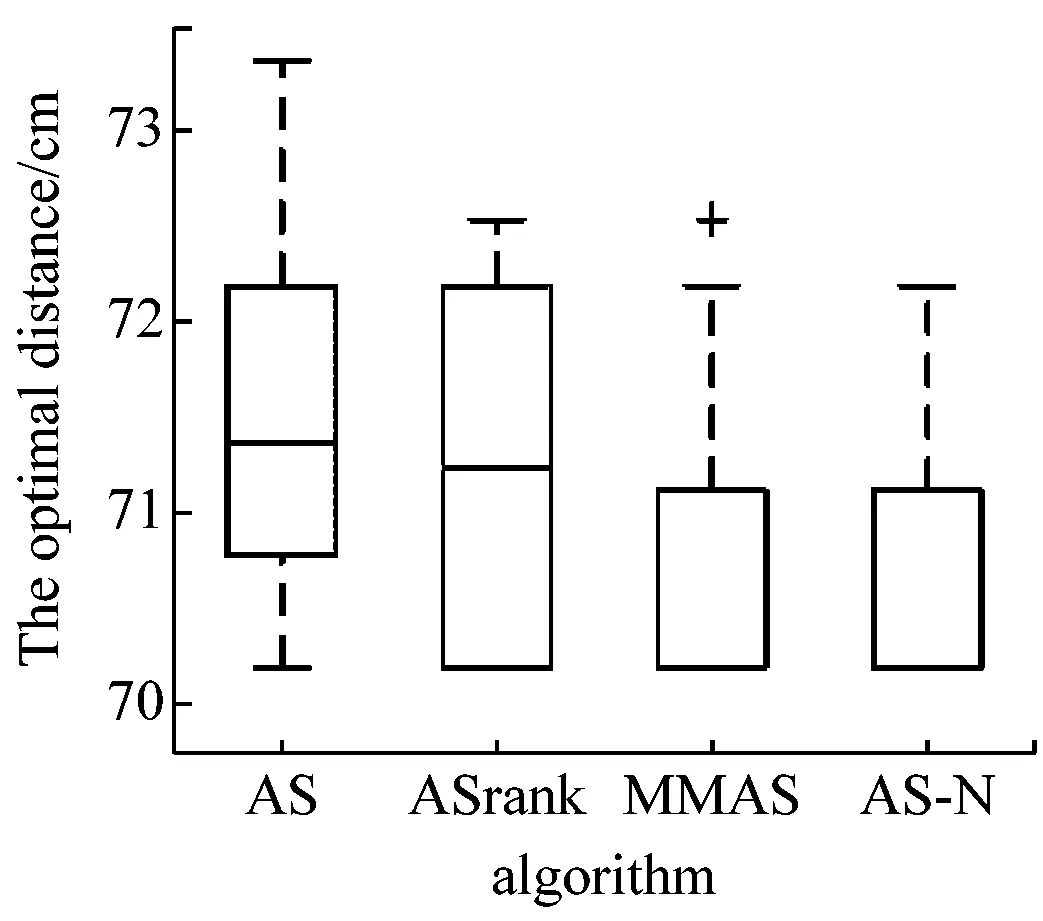
通过对这三种复杂环境下盒图比较可知,如图6所示。

在所选4种算法中，AS-N算法在复杂状态下能获得显著的优势。依次挑选30组数据进行分析，在复杂问题1下，AS-N算法只获得一次脏数据，其他几种算法，处在这种复杂问题条件下，极易陷入局部最优解的几面，其性能远远比不上改进的AS-N算法。在复杂问题2和3环境下，AS-N算法依然能获得理想的效果。

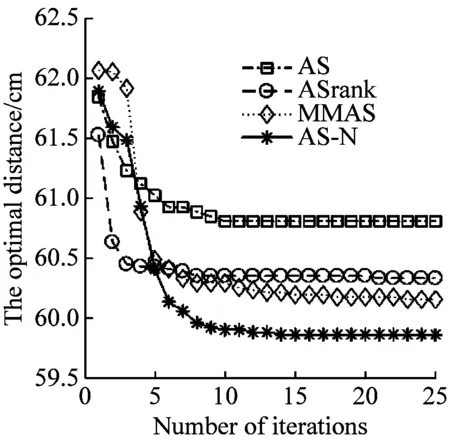
图5 不同复杂环境下4种算法收敛情况

(a) 复杂环境1

(b) 复杂环境2

(c) 复杂环境3

图6 三种复杂环境下3盒图比较效果

4 总结

总之，随着现代科学技术的迅速发展，高科技技术也得到更广泛的使用。路径规划技术是机器人以及人工智能研究较为重要的研究领域，其对于提升机器人功能等方面发挥着重要的作用。如今，蚁群算法已经被广泛用来解决各领域的路径优化问题，尤其在工程设计领域有着更广泛的运用。本次研究针对传统蚁群算法极易陷入局部的最优解问题，提出添加负反馈机制的优化蚁群算法，这种新机制的应用优势在于，当每一代结束后，蚂蚁不单在找出的最优路径上释放相应地信息素，并在最差路径上释放出负反馈信息。研究结果表明，将这种改进的蚁群算法用于机器人路径规划中，有利于指导蚁群优化环节探索未知的领域，以此获取最优的路径。