电工电子产品振动试验能力验证方法

张浩

四川省电子产品监督检验所 四川成都 6 10100

电工电子产品在出厂之前，为了保证其稳定性以及可靠性，需要针对各项参数进行周密的检测，而环境测试就是最为基础的一种，其主要的目的就是检查该产品对于实际工作环境的适应能力。而在环境试验当中，正弦振动测试就是非常重要的一个环节，通过模拟各种实际生活中的振动，比如旋转、震荡、脉冲振动等确保产品在工作中不会因振动问题而出现失灵的情况。

1 正弦振动实验介绍

想要了解正弦振动试验的具体试验方式以及对于试验结论的分析，先要了解什么是正弦振动试验。简单来说，这种试验就是在特定的试验室当中，让待检测电子产品处于模拟工作的状态中，同时利用适合的振动试验台来制造出电子产品在使用、运输以及贮藏过程中可能受到的振动，观察在不同类型的振动中电子产品所发生的变化。由于电工电子产品具有比较固定的使用环境与应用范围，因此在试验的过程中，通过调整位移幅度值以及加速度等参数，就可以得到较为可靠的试验数据[1]。

2 振动对电工电子产品的影响

电工电子产品由于其内部存在大量精密零件，且自身体积小，在受到各种不同的振动或者冲击的情况之下会对其性能产生严重影响。从总体上来说，振动对于电工电子装置所带来的影响主要有三种。首先是对电子产品内部结构造成物理性的破坏，比如断裂、拉伸、变形等，这种破坏具有永久性，通常情况下只能通过更换的方式来解决。其次是工作性能受到影响，在高频振动影响之下，电子设备内部的元器件可能发生微小的位移，可能导致元器件之间的连接突然断开，造成接触不良的情况，让其处于不稳定的工作状态中。最后，振动可能会导致电子产品工艺性损伤，比如说螺丝的松动或者是脱焊等问题，虽然工艺问题处理起来比较简单，但是发生的频率比较高，对产品的正常使用也会产生一定的消极影响。

3 电工电子产品检测过程

为了更好地说明振动试验的运行方式，我们以某振动测试盒的安装以及运行为例子。该测试盒带有一个振动探头，其作用是检测X、Y、Z三个方向的加速度。其中X轴与Y轴呈现出水平垂直关系。此次检测依据GB/T2423.10《环境试验 第2部分：试验方法 试验Fc：振动（正弦）》中的相关参数进行（如表1）。在样品的安装环节，试验人员需要用胶水把振动测试探头固定在振动工作台的中心，同时将该探头的另一端与振动测试盒相连。在连接完成之后，工作人员可以给测试盒供电，在本次试验中采用的电源为220V-50Hz，在其处于静止状态的时候启动电源，此时测试盒上的显示器显示出具体数值，表明其处于正常工作状态中[2]。当试验正式开始之后，试验人员需要在试验进行到第4分钟的时候记录显示器上所呈现的在X、Y、Z三个方向上的加速度。

4 分析结果

4.1 评价原则

在得到了试验数据之后，工作人员就要开始对试验数据进行分析。在本次试验当中，分别将X、Y、Z三个轴方向的振动加速度作为检测对象，依照《能力验证结果的统计处理和能力评价指南》中的统计方式进行计算，得出测试盒能力评定的标准差以及指定数值，以试验室Z比分数对其进行推算，Z比分数的公式为Z=（x-X）/δ。在这个公式中，x表示本次试验最终测得的数值，X表示试验指定值，也就是试验结果数值的稳健平均值，而δ则代表能力评定的标准差。

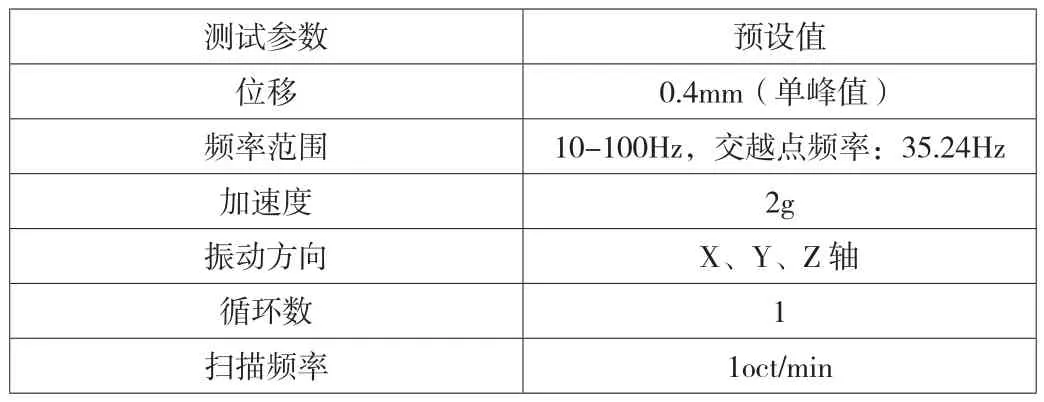
表1 正弦振动试验参数

4.2 参数设计

在正弦振动测试中，正弦扫频振动常常会由于参数设置出现错误而影响到扫频振动结果，其主要原因在于交越点前的位置数值在设定的时候出现问题。一般情况下，在设计振动试验目标谱过程中，其数值应为位移峰值（p-p）[3]。但在实际试验过程中，很多测试大纲当中所记录的都是位移的单峰值。因此需要通过校准交越点的位移值来提升扫频振动数值的精度，确保振动台检测目标谱的正确性。

4.3 Z比分数演算

在此次试验当中，三个方向上的加速度稳定平均值为λ，稳健标准差为ε，而X、Y、Z三个方向上的加速度数值为x（如表2），那么根据Z比分数公式，可以得到其在三个不同方向上的加速度Z比分数数值：Zx=0.6，Zy=0.9，Zz=0.2，三个数值均小于2，代表三个试验结构均为满意。

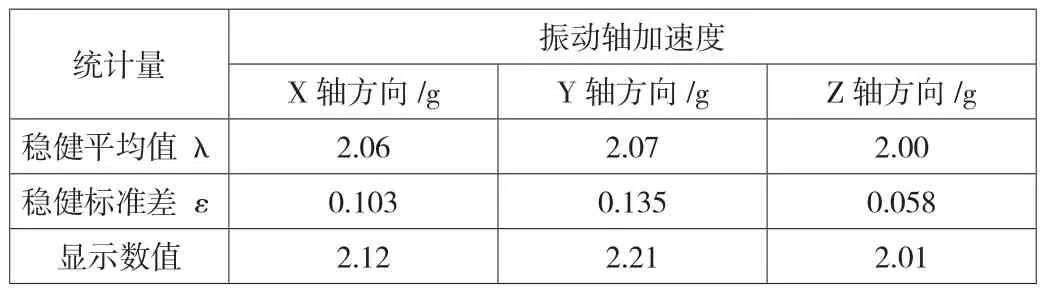
表2 稳健平均值、标准差与显示数值在X、Y、Z三个方向上的加速度

5 结语

在进行电工电子产品振动试验过程中，根据X、Y、Z轴方向加速度的Z比分数，可以验证振动试验的能力，保证其试验结果的精准性。此外，为了提升试验成功率，在要严格按照相关规定来安装样品，并且对控制传感器等装置进行科学的保养，保证试验能够顺利进行。