去掉多余杆件的方式计算超静定桁架结构内力

鲁丽君 张东焕 王春光 杨志刚

摘 要：文章介绍了采用去掉多余约束杆件的方式计算超静定桁架内力的计算过程。以一次超静定桁架为例，去除多余约束杆件并分别按相对、相背离两种方式假设广义多余未知力方向，详细介绍了两种情况下的位移协调条件的分析过程，建立了相应的力法方程;并对两种情况下的力法方程进行求解计算，得出互为反号的内力计算结果，同时对计算结果进行了分析，得出了完全一致的计算结论。

关键词：超静定桁架;多余杆件;方向假设;内力计算

中图分类号：O342

文章编号：2095-624X（2019）06-0142-03

用力法计算超静定桁架结构内力时，解除多余约束的方式有两种：一种是切断多余约束杆件，一种是去掉多余约束杆件。这两种不同的解除约束的方式所对应的位移协调条件不一样，建立的位移协调方程（即力法方程）不同。其中去掉多余约束杆件的解除约束方式在建立力法方程时对学生知识综合运用能力要求较高，需要综合运用前期所学的《理论力学》《材料力学》知识，正确分析位移协调条件，才能建立出力法方程。这比采用切断多余约束杆件的方式建立力法方程要困难得多，而现有的各种《结构力学》教材以及相关辅导资料中很少有采用去掉多余约束杆件的方式计算超静定桁架内力的讲解。李廉锟编著的《结构力学》第六版[1]例题7-2采用切断多余约束杆件的方式讲解了一次超静定桁架结构内力的计算过程，但对去除多余约束杆件的方式只给出了方程，而没有讲解方程的建立过程。这里以该例题为例，详细讲解采用去掉多余约束杆件的方式计算该超静定桁架结构内力的步骤与过程。

一、 建立力法方程

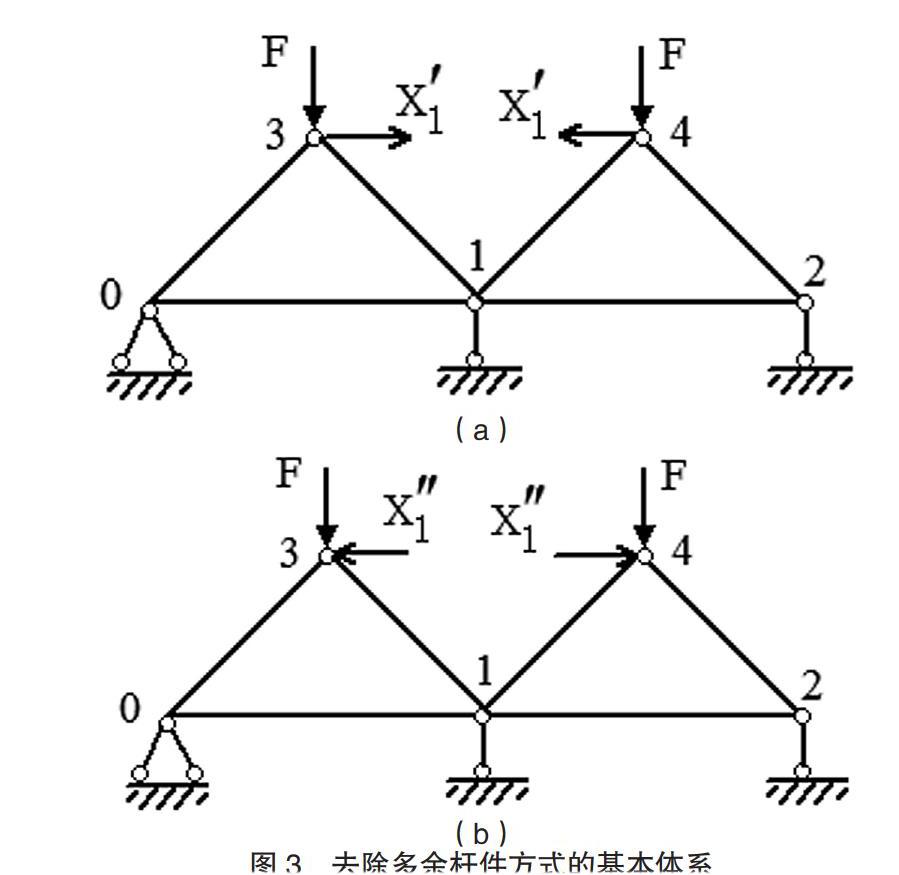
李廉锟编著的《结构力学》第六版例题7-2，原结构为一次超静定桁架（图1）。采取去掉上弦杆34的方式解除多余约束，得到一次超静定桁架的基本结构（图2）。去掉的弦杆34用作用于结点3、4的广义多余未知力（一对大小相等、方向相反沿上弦杆34轴向的力）代替，由于广义多余未知力未知，它的方向可按相向（图3（a））和背离（图3（b））两种情况假设，而得到图3所示的超静定桁架结构的基本体系。基本体系的受力与原结构（图1）等效，即问题转化为图3（a）、图3（b）所示结构体系的计算。为了方便后续分析对比，图3（a）和图3（b）中广义多余未知力分别用X、X表示，下面分别讨论这两种不同方向假设下的力法方程。

1.广义多余未知力指向——相向

基本体系如图3（a）所示，根据位移协调条件：基本体系中与广义多余未知力对应的变形应与原结构相应的伸缩变形相同。去掉上弦杆34后（图3（a））与广义多余未知力X对应的变形为3、4结点的相对水平位移，它应该与原结构（图1）上弦杆34的变形相同。

基本体系在X和结点3、4上的外力F共同作用下所产生的3、4结点间的相对水平相对位移，根据叠加原理等于X与荷载F分别作用时产生的位移之和，即δX+△;

δ——系数。单位多余未知力——即令X=1时所引起的沿X'1方向的位移;

△——自由项。外荷载集中力F所引起的沿X方向的位移;

原结构3、4节点的相对水平位移即为弦杆34的轴向变形记作△1。根据多余未知力相向假设（图3（a）），可推知上弦杆34受力方向如图4——弦杆34上的力与图3（a）中的廣义多余未知力X互为作用力与反作用力[2]：

建立力法方程时结点3、4的相对水平距离以与图3（a）所示基本体系中广义多余未知力方向一致为正，即结点3、4的相对水平距离以相对缩小为正;而由图4可知弦杆34受拉，杆件伸长，即原结构（图1）结点3、4的相对水平距离增大，因此根据位移协调条件：结点3、4的相对水平位移为负值。力法方程如下：

2.广义多余未知力指向——背离

同理基本体系（图3（b））中，与广义多余未知力X对应的变形为3、4结点的相对水平位移应与原结构（图1）上弦杆34的伸缩变形相同。基本体系在多余未知力X和结点3、4上的外力F共同作用下，根据叠加原理，与广义力X对应的3、4结点间的相对水平相对位移为δX+△;系数δ，自由项△含义与2.1中的δ，△相同，即

δ——系数。单位多余未知力——即令X=1时所引起的沿X方向的位移;

△——自由项。外荷载集中力F所引起的沿X方向的位移;

根据多余未知力相背离假设（图3（b）），可推知原结构上弦杆受力如图5——弦杆34上的力与图3（b）中的广义多余未知力X互为作用力与反作用力，弦杆34的轴向变形记作△1：

根据图3（b）建立力法典型方程时，结点3、4的相对水平距离以与图3（b）所示基本体系中多余未知力方向一致为正，即结点3、4的相对水平距离以增大为正。而由图5可知原结构上弦杆34受压，杆件压缩，结点3、4的相对水平距离减小。同理根据位移协调条件：结点3、4的相对水平位移为负值，力法方程如下：

根据广义多余未知力指向——相向与广义多余未知力指向——背离的分析对比发现：去除多余约束杆件34，广义多余未知力不论按图3（a）相向假设还是按图3（b）背离假设，位移协调条件是一样的，与多余广义未知力的方向假设无关。将力法方程（1）与方程（2）进行移项整理得到如下方程：

二、力法方程求解

根据《结构力学》知识，系数δ、δ和自由项△、△的计算公式如下：

F、F——单位广义多余未知力单独作用时，即X=1、X=1单独作用在基本结构（图2）上时所引起的各杆件的内力值;

F、F——3、4结点集中力F单独作用时所引起的基本结构（图2）中各杆件的内力值;

1——基本结构（图2）中各杆件的长度;

EA——基本结构（图2）中各杆件的材料常数。

根据公式（5）和公式（6），计算基本结构（图2）分别在单位广义多余未知力X=1;3、4结点荷载F作用下各杆的内力F、F，计算结果如图6所示。各杆件杆长数据、内力计算结果汇总列于表1。

同样计算基本结构（图2）分别在单位广义多余未知力X=1;3、4结点荷载F作用下各杆的内力F、F，计算结果如图7所示。各杆件杆长数据、内力计算结果汇总列于表2。

根据系数计算公式（5）和表1与表2中内力和杆长数据计算可得：

同理根据自由项计算公式（6） 和表1与表2中内力和杆长数据计算可得：

将系数和自由项计算结果代入方程（3）和方程（4）并消去相同参数EA可得：

求解方程（7）和方程（8）可得：

X与X绝对值相等，异号。X计算结果表明：多余未知力的方向与X假设方向相同，即弦杆34受力如图4，弦杆34承受拉力;X计算结果则表明：多余未知力方向与X方向相反，即弦杆34实际受力与图5方向相反，同样可推知弦杆承受同样大小的拉力，计算结论完全一致。

去除多余约束杆件方式求解超静定桁架结构的关键在于建立位移协调方程时与所解除约束对应的位移数据的确定——即方程（1）和（2）等号右边数值的确定，特别是数值正负号的确定。去除多余约束杆件后广义多余未知力分别按相向和相背离假设，在分析位移协调条件时略有差异——正、负号处理上的差异，但最后分析得出的位移协调条件——方程（1）和方程（2）完全相同，即位移协调方程与广义多余未知力的方向假设无关。

虽然采用力法计算超静定桁架结构内力时，切断多余杆件方式建立位移协调方程——即力法方程相对更容易;但去除多余杆件方式的分析和求解过程有助于加强对力法基本思想的理解，加深对力法位移协调条件的认识，从而更好地掌握和运用力法。

参考文献：

[1]李廉锟.结构力学（上册）（第6版）[M].北京：高等教育出版社，2017.

[2]哈尔滨工业大学理论力学教研室.理论力学（I）（第7版）[M].北京：高等教育出版社，2009.

[3] 孙训方，方孝淑，关来泰.材料力学（I）（第5版）[M].北京：高等教育出版社，2009.

作者简介：鲁丽君（1977—），女，山东理工大学建筑工程学院讲师，研究方向：结构疲劳损伤预测与评估。