基于风险系数的天然气水合物生成风险评估方法

马楠 李军 刘书杰 文敏 陈欢

(1. 中国石油大学(北京)， 北京 102200； 2. 中海油研究总院， 北京 100029)

水合物风险评估内容主要包括水合物生成位置预测、水合物生成量预测及水合物生成速度预测。在实际生产过程中，施工方只需确定水合物的生成位置，并在该位置处加入足量抑制剂，即可预防由于水合物生成而导致的一系列井下安全问题。水合物生成位置的预测是水合物风险评估工作的重点研究内容[1-2]。通过水合物生成位置预测研究，井筒温度-压力模型和水合物生成条件预测模型得到不断修正，计算过程逐步优化，模拟结果与实际情况的吻合度不断提高[3-6]。

在实际生产中，特定位置处水合物生成的可能性更受关注，但关于其风险量化评估的研究不多。本次研究将以南海油田某油气井资料为基础，应用PIPE Sim软件计算该井浅部井段的温度值和压力值，并通过计算模型进行验证[7]。通过研究，提出了风险系数的概念，量化水合物风险，简化了评估方法。

1 井筒温度压力的预测及验证模型

1.1 井筒温度和压力预测

该井所处水深为329 m。在本模型中，地层热导率为5 W/(m2·K)，套管内径为205.7 mm，油管内径为100.3 mm，管壁粗糙度为25.4 μm。以海底泥线处为零点，利用PIPE Sim软件计算生产后期井筒内的压力值和温度值，观察压力和温度随深度的变化曲线(见图1和图2)。

图1 井筒压力随深度变化曲线

图2 井筒温度随深度变化曲线

1.2 井筒温度验证模型

当气体从井底沿井筒向上流动时，由于井筒周围地层之间存在温差，因此必然通过导热、对流和辐射等3种传热方式向周围地层传热[8]。将三维热扩散问题简化为一维径向热流，作以下假设：(1) 水合物生成过程中的动能可忽略不计；(2) 地温按线性分布，且井底流体温度等于地层温度；(3) 井筒及地层中的热损失是径向的，不考虑沿井深方向的传热，且井筒中任意截面上各点的温度均相等。井筒流体向外传递热量时，由于热对流和热辐射占总传热的比例很小，因此可以忽略不计[9]。在此，计算海床以下部分的控制体与井筒流体瞬时传热速度qh：

dqh=(2πrt)dhUo(Ts-Th)

(1)

式中：rt—— 油管内径，m；

h—— 深度，m；

Ts—— 井筒内流体温度，℃；

Th—— 水泥环与地层交界处的温度，℃；

Uo—— 井筒总传热系数，J/(m2·s·℃ )。

钢材具有很高的热导率，因此油管和套管的热阻可忽略不计[10]，则Uo计算式为：

(2)

式中：kan—— 环空导热系数，J/(m2·s·℃ )；

kcem—— 水泥环导热系数，J/(m2·s·℃ )；

rto—— 油管外径，m；

rci—— 套管内径，m；

rco—— 套管外径，m；

rwb—— 裸眼井径，m。

井筒周围地层中的热传导过程为不稳定传热过程，因此，采用Ramey近似公式计算地层瞬时传热速度qe：

(3)

f(td)≈0.5 lntd+0.403

(4)

(5)

式中：ke—— 地层导热系数，J/(m2·s·℃ )；

Te—— 地层温度，℃；

t—— 热扩散时间，s；

ρe—— 地层岩石密度，kg/m3；

Ce—— 地层岩石比热，J/(kg·℃ )；

td—— 无因次时间。

由式(1)、(3)得到井筒流体在海床以下部分的总瞬时传热速度计算式：

dq=(2πrt)dhUo(Ts-Th)+

(6)

根据能量和温度的关系，得到控制体温度变化的计算式：

dT=dq/(Cmw)

(7)

式中：Cm—— 井筒流体的定压比热，J/(kg·℃)；

w—— 流体质量流量，kg/s。

对于海床以上部分，考虑到深海油气井有很长一部分井段在隔水套管中，将其温度计算公式改写为：

dq=(2πrt)dhUg(Ts-Tg)+

(8)

(9)

(10)

式中：kw—— 海水导热系数，J/(m2·s·℃ )；

kg—— 隔水管导热系数，J/(m2·s·℃ )；

Tg—— 隔水管与海水交界处的温度，℃；

Tw—— 海水温度，℃；

rgi—— 隔水管内径，m；

rgo—— 隔水管外径，m；

Ug—— 隔水管总传热系数，J/(m2·s·℃ )；

ρw—— 海水密度，kg/m3；

Cw—— 海水比热，J/(kg·℃ )。

1.3 井筒压力验证模型

井筒压力的计算方法有很多种，其中Cullender和Smith提出的计算模型[11]应用较为广泛，我们称其为Cullender & Smith模型。在油气井产出物从井底沿油管流到井口的总能量消耗过程中，动能损耗非常小，可以忽略不计。气体稳定流动能量方程式可简化为：

(11)

式中：ρ—— 气体密度，kg/m3；

vg—— 气体流速，m/s；

f—— Moody摩阻系数。

式(11)在任何(p，T)状态下都能成立，由此可推导出Cullender & Smith井筒压力计算模型：

(12)

式中：Z—— 气体偏差系数；

qsc—— 日产气量，m3/d；

fg—— 气体摩阻系数；

pwf—— 井底流压，MPa；

pFTP—— 井口流动压力，MPa；

γg—— 气体相对密度；

p—— 任意井深处井筒内流体压力，MPa；

T—— 任意井深处井筒内流体温度，℃。

为了避免天然气中的凝析水和凝析油影响计算结果的准确性，对Cullender & Smith模型作了修正，得到以下井筒压力分布公式：

(13)

式中：fgl—— 含水气体摩阻系数；

FL—— 气体含液校正系数。

在实际生产过程中，通常更关注水下井口、防喷器及井下安全阀等设备是否有水合物生成。这些设备所处位置深度较浅，大概在泥线以下0～600 m。根据前面计算得到的压力值和温度值，利用计算模型进行验证。对比软件与验证模型所得结果(见图3和图4)，认为通过软件计算出的压力值和温度值与通过验证模型计算的值较为接近。

图3 软件与验证模型计算压力值的比较

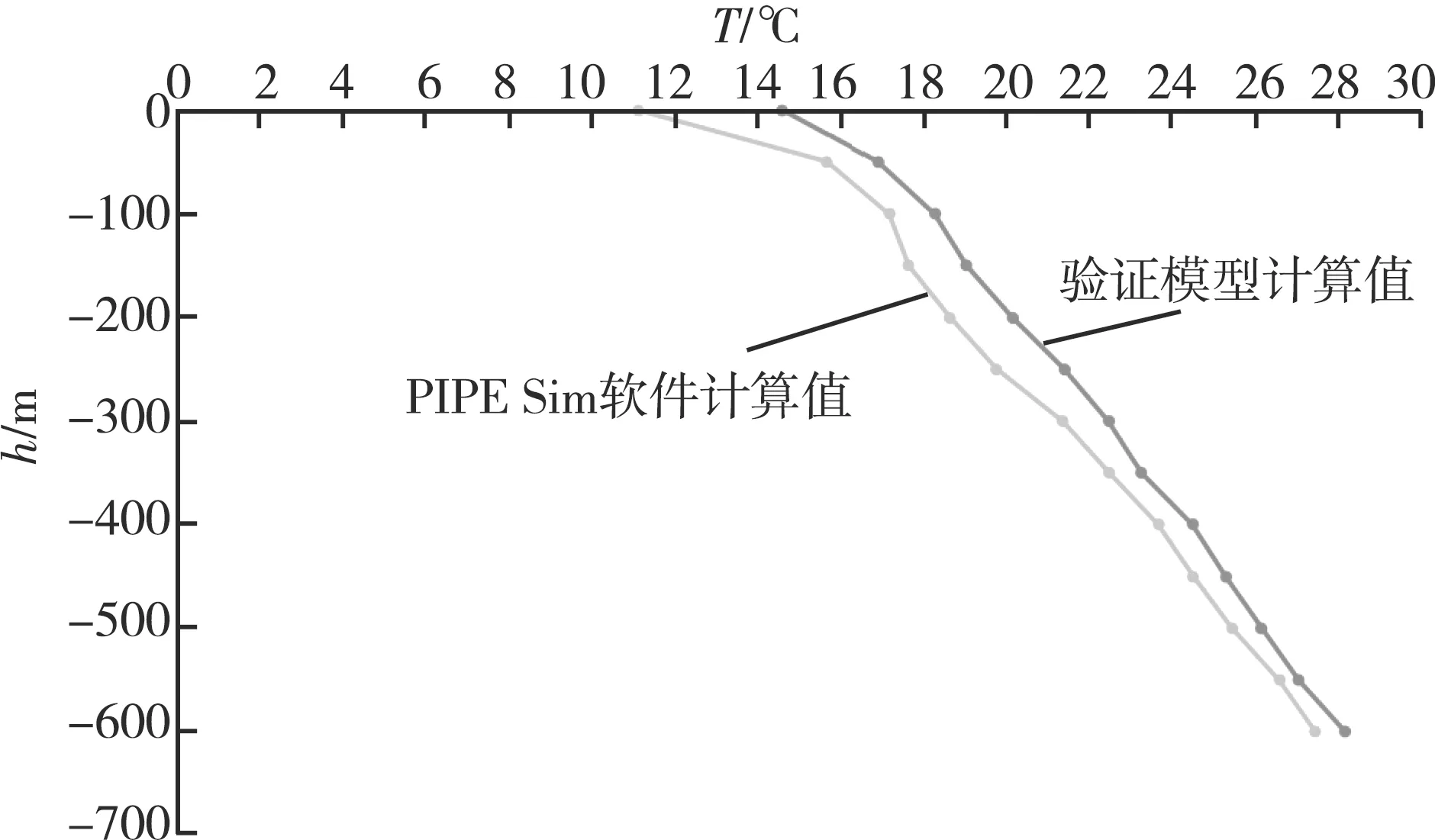
图4 软件与验证模型计算温度值的比较

2 水合物相态曲线绘制

目前，确定水合物生成条件的方法大致可以分为图解法、经验公式法、平衡常数法和分子热力学法等[12-13]。其中，分子热力学方法推导过程严密，计算结果准确度高，常应用于水合物生成条件预测研究[14-15]。

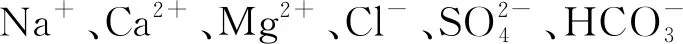
图5 水合物相态曲线

3 水合物风险简化评估方法

根据水合物风险评估示意图，观察对比井筒温-压曲线和水合物相态曲线，即可快速判断出目标位置是否有水合物生成，以及水合物生成的大致位置范围。

图6中，水合物生成条件曲线左侧的井筒温-压曲线所代表的深度处将会生成水合物，而水合物生成条件曲线右侧井筒温-压曲线所代表的深度处暂时不会生成水合物，但具有水合物生成的可能性。

风险系数可以作为水合物风险评估的依据，其计算方法具体如下：

(14)

式中：Twell—— 井筒内某深度处温度，℃；

TTbalance—— 井筒内某深度处水合物生成温度，℃；

b—— 过冷度安全余量，工程实践中取5℃；

a—— 水合物风险系数。

结合井筒各深度处的温度和水合物的生成温度，利用式(14)计算其各深度处的风险系数。根据计算所得风险系数绘制水合物风险评估曲线(见图7)，评估风险大小。

图6 水合物风险评估示意图

图7 水合物风险评估曲线

(1) 当风险系数为负数时，代表该深度处将会有水合物生成，需采取措施及时防治。

(2) 当风险系数为正数时，代表该深度处暂时不会生成水合物。风险系数越接近零，水合物生成的可能性越大。当风险系数大于1时，水合物生成的可能性较小，且随着风险系数的增大，水合物生成可能性减小。

(3) 在泥线以下0 — 309 m，风险系数均为负数，此深度范围内将会有水合物生成。在泥线以下309 — 600 m深度范围内，风险系数均为正，此深度范围内暂时不会生成水合物；但风险系数的数值较小(均未超过0.5)，生成水合物的可能性极大。

根据水合物风险评估曲线判断，该井在泥线以下0 — 600 m深度范围内的生产设备受到水合物危害的可能性较大。建议对水下井口、防喷器及该范围内的井下设备进行定期检测，适当注入水合物抑制剂，及时预防由于水合物生成引发的井下安全问题。

4 结 语

本次研究中提出了风险系数的概念及水合物风险评估简化方法，对水合物风险进行了量化。以南海油田某油井为例进行评估，认为在生产后期，该井浅部井段(0 — 600 m深度范围)受到水合物危害的可能性极大。建议对该深度范围内的生产设备进行定期检测，及时处理因水合物生成而引发的井下安全问题。需要说明的是，不同生产井的井况有所不同，具体的风险系数需结合实际生产数据进行计算分析。