平面含复铰杆组拓扑结构的同构判定方法*

张 瑶，孔建益，孙亮波，刘怀广，刘源泂

(1.武汉科技大学 机械自动化学院，武汉 430081；2.武汉轻工大学 机械工程学院，武汉 430038)

0 引言

杆组是组成机构的基本元素之一，机构的组成理论[1]指出任何机构都可以由若干个基本杆组联接机架和主动件得到，这一机构形成过程简单且直观。李树军[2-4]提出平面机构综合方法，将基本杆组、主动件、机架作为矩阵基本元素进行排列组合得出机构，这种组合方式简单、实用，同时给出了机构识别的思想。曹毅等[5]在李树军的机构综合方法研究基础之上，加入了复铰因子参数，获得了八杆含复铰的机构构型综合。EE Peisakh[6]提出了Assur杆组的型综合算法和识别构型方法，使得型综合计算机自动化。孙亮波等[7-8]在杆组型综合方面取得了很多成果，得到了2～10杆的单铰杆组拓扑图库以及6杆含复铰杆组图库。韩建友等[9]运用拆分法在机构中拆分得到杆组，并采用关联和邻接矩阵特征值特征向量来判定同构，但未涉及含复合铰链的复杂杆组的获得。

同构判定是型综合中重要步骤，关于运动链同构的研究成果有很多，但不适用于杆组，一般我们讨论的运动链都是闭式运动链，而杆组是含有两个以上外接运动副的非闭合链，随着杆组中构件数目的增多，杆组结构复杂度增大，无可避免的会出现同构现象，所以针对杆组的同构判定方法是不可或缺的。文献[10]中提及了同构运动链其邻接矩阵特征值和特征向量的充分必要条件，该方法是判断同构最简便的方法之一，但不适合杆组的识别。

本文根据描述杆组结构特征的双色拓扑图，构造了拓展的邻接矩阵。基于杆组拓展邻接矩阵表达杆组结构中构件、复铰以及外接运动副的自身信息，和三者之间的连接关系。之后结合杆组拓展邻接矩阵中包含的杆组结构信息以及连接信息，利用矩阵特征值特征向量[10]来判断杆组结构是否同构，解决了含有复合铰链的复杂杆组同构问题。

1 含复铰杆组的拓扑结构特征

为了保证杆组特征信息得到充分表达，寻求一种杆组拓扑图描述方式尤为重要。杆组中的结构特征信息包括构件数(n)、复铰数(J)、运动副数(P)、环路数(Lg)、外接运动副数(pe)等。双色拓扑图是一种普遍用来表示含复铰结构的拓扑图表示方法，含复铰的杆组用实心和空心圆点分别表示构件和复铰，构件与复铰之间连接的线段表示内接运动副，圆点上引出的线段表示外接运动副。下图是杆组拓扑结构中n=6、J=1、P=9、Lg=2、pe=2的双色拓扑图。

(a)结构简图 (b)双色拓扑图图1 杆组的表示

这种双色拓扑图的表示方法相较于杆组结构简图，能清晰直观的表达了杆组中复铰和外接运动副等重要的结构特征信息，有利于后续同构判定和型综合的完成。

2 杆组拓展邻接矩阵的构建

2.1 拓展的邻接矩阵

为了便于杆组结构信息的描述以及后续杆组同构识别的计算机处理，构建了拓展的邻接矩阵，假设杆组结构拓扑图中有n个构件，J个复铰和pe个外接运动副组成，则可以用A=[ai,j]表示，其中i,j=1,2,3,…,(n+J+pe)，拓展的邻接矩阵的数学表达式如式(1)：

(1)

式(1)中d表示复铰连接的构件数目，即复铰的元数。一般地，邻接矩阵是用于表示运动链中构件与构件之间的关系，而杆组拓展的邻接矩阵表示构件、复铰、外接运动副三者之间的关系。矩阵中非对角线元素表示的构件、复铰、外接运动副之间是否连接，对角线元素为0。图1中的杆组有一个三元复铰，则d=3，它的拓展邻接矩阵见式(2):

(2)

2.2 矩阵的性质

(1)矩阵的阶数等于杆组结构中构件数、复铰数以及外接运动副数三者之和；

(2)矩阵中i行(列)中“1”的个数m≥2时，则该行(列)表示的是构件，其中m是构件的元数；

(3)若矩阵i行(列)中“d”的个数t≥2时，则该行(列)表示的是复铰，其中t是复铰的元数；

(4)若矩阵中i行(列)有且仅有一个“1”，则该行(列)表示杆组的外接运动副，且该外接运动副连接位置在元素“1”对应的列(行)构件上。

例如式(2)的矩阵，表示对应的杆组拓扑图中构件数、复铰数、外接运动副数的和为8，即n+J+pe=8。矩阵中第一行中元素“1”的个数m=3，则该行表示的是三元构件；矩阵中第七行中“3”的个数为t=3，所以该行代表的是三元复铰；第7、8行中只有一个元素“1”，则它们表示的是外副。式(2)中的具体杆组结构信息如表1所示。

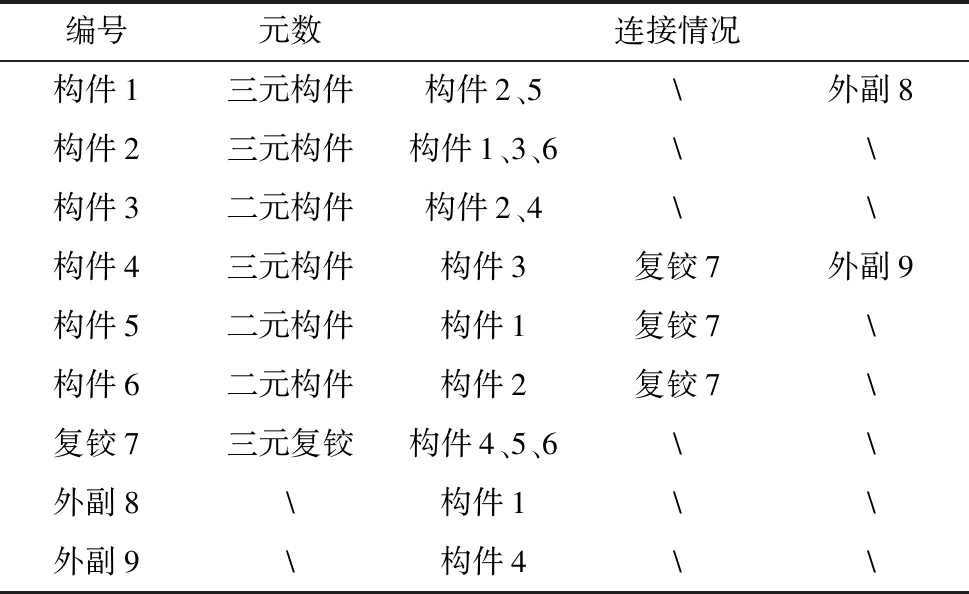
表1 矩阵包含信息

3 杆组结构的同构判定及案例

3.1 同构判定步骤

两杆组是否同构，可按照如下步骤来判定：

(1)对杆组拓扑图的构件、复铰及外接运动副进行任意编号;

(2)比较杆组结构中构件数(n)、复铰数(J)、外接运动副数(pe)，若三个数不相等，则异构；若不相等，则进行下一步;

(3)构建杆组拓展的邻接矩阵，得到杆组结构信息列表，比较列表中的信息，若不同，则异构；若相同，则进行下一步;

(4)求出拓展的邻接矩阵的特征值λ，特征向量ξ，若特征值不完全相同，则异构；否则，进行下一步;

(5)若两杆组的特征向量矩阵[ξ1,ξ2,…ξi…,ξN]可以通过若干行列变化得到另外一个特征向量矩阵，则同构；反之，异构。之后根据上述变化矩阵找到同构杆组中对应的构件、复铰及外接运动副。

3.2 案例

以图2三个含复铰的八杆杆组为例，进行同构判定。首先对拓扑图中构件、复铰、外接运动副进行任意编号1～11(n+J+pe=11)。

图2 8杆杆组

然后，构建杆组拓展邻接矩阵(11阶)，杆组(1)拓展的邻接矩阵Ac1，表2是矩阵中包含的杆组信息。

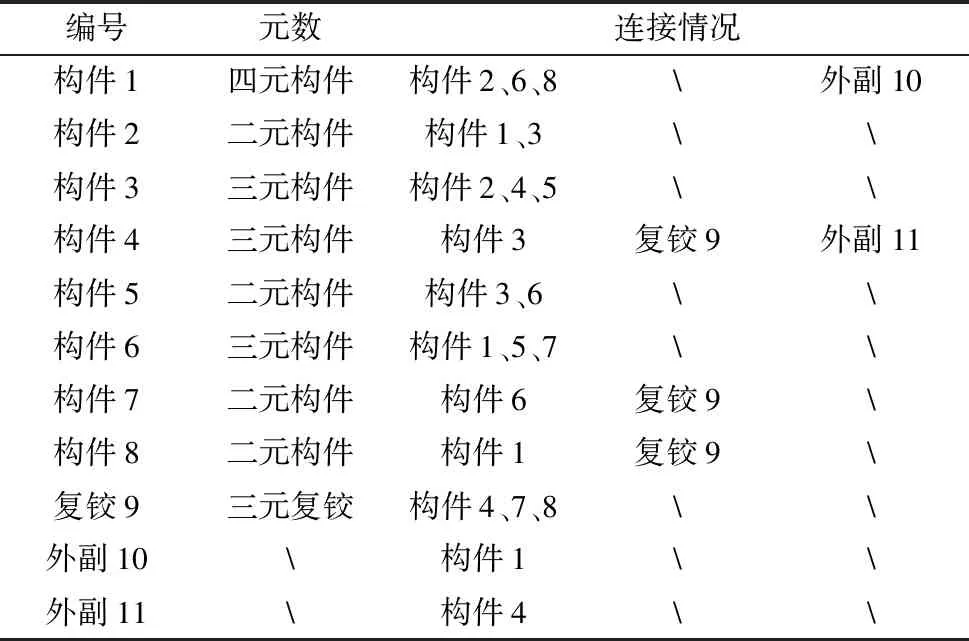
表2 Ac1矩阵中杆组包含信息

从表2中可知图2中杆组(1)的构件、复铰、外接运动副的数量类型以及它们之间的连接情况，下面是杆组(2)、(3)对应的拓展邻接矩阵Ac2、Ac3，表2、表3是矩阵中Ac2、Ac3包含的杆组结构信息。

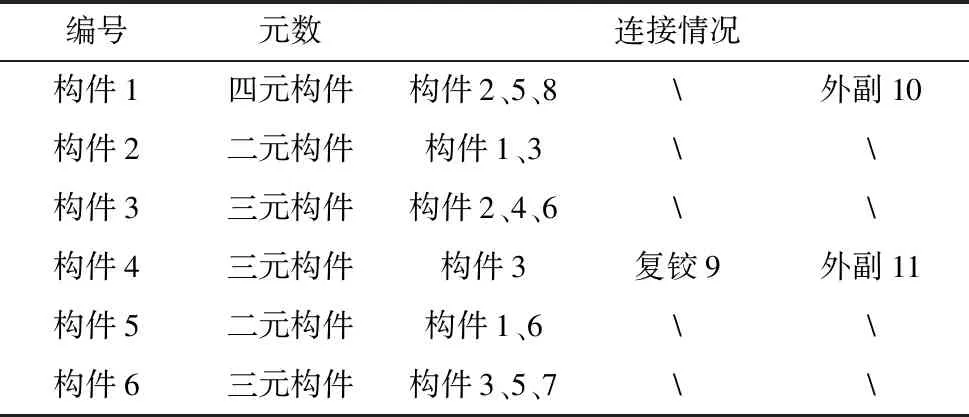
表3 Ac2矩阵包含信息

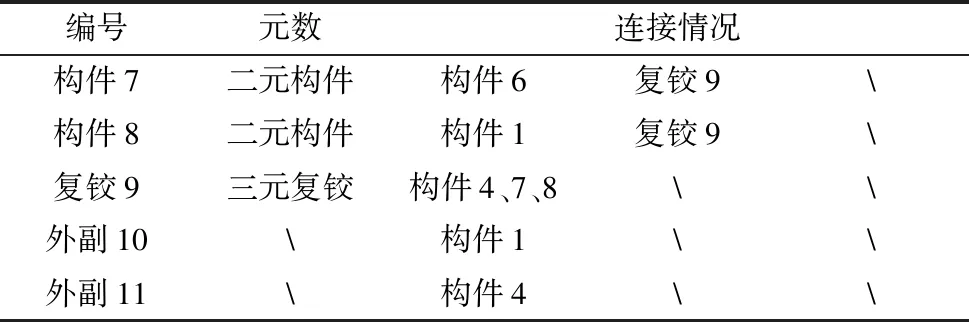
续表

表4 Ac3矩阵包含信息

比较3个表格中各杆组中的信息，发现构件、复铰、外接运动副各自的类型数目均相同，构件数n=8(二元构件1个、三元构件3个、四元构件1个)，复铰数J=1(三元复铰)，外接运动副数pe=2。它们的连接其他结构的情况都相同，例如四元构件都是连接3个二元构件和1个外接运动副。转(4)。

计算机编程求取矩阵Ac1、Ac2、Ac3的特征值和特征向量，杆组(1)、(2)、(3)的特征值分别用λ1、λ2、λ3表示如下:

可知3个特征值λ1≠λ2=λ3，则杆组(1)与杆组(2)、(3)不同构。矩阵Ac2、Ac3的特征向量矩阵分别用P2、P3表示如下，矩阵P2、P3不完全相同，此时仍不能判断杆组(2)和杆组(3)是否同构，需要进行步骤(5)，特征向量矩阵P2或P3经过行列变化后，是否能相等。

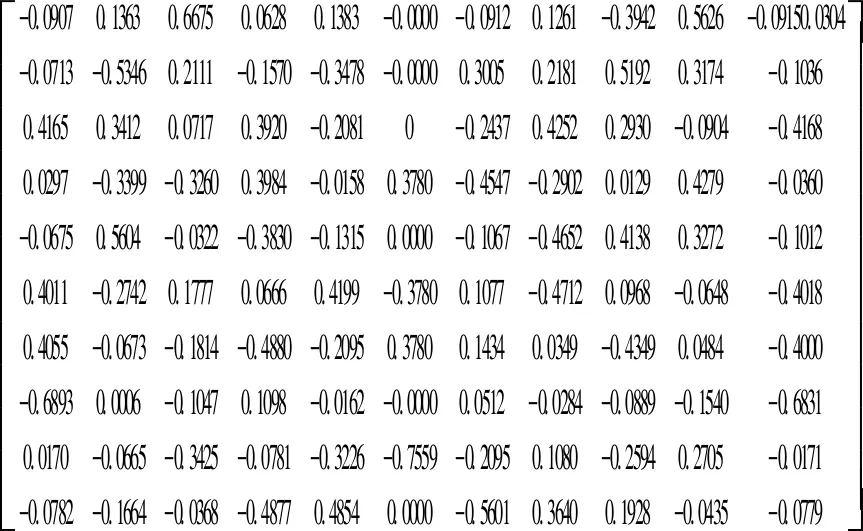
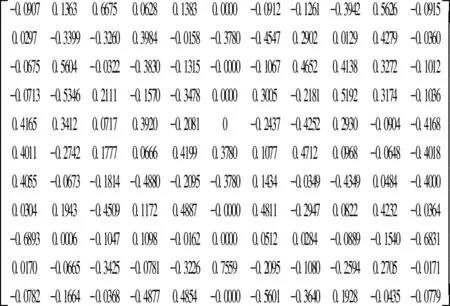
上述矩阵Ac3的特征向量矩阵P3和矩阵Ac2的特征向量矩阵P2具有6组行对应关系，映射到杆组拓扑结构中，即是杆组(2)和杆组(3)的构件、复铰、外副之间的对应关系。E11(i,j)表示的是11阶单位矩阵中的i、j行互换，验证可知存在矩阵B使得BAc3B-1=Ac2。其中矩阵B为：

B=E11(7, 8)E11(6, 8)
E11(5, 8)E11(4, 5)E11(3, 4)E11(2, 8)

由此可以得出杆组(2)和杆组(3)同构，且可得出两者构件、复铰和外接运动副编号对应关系如表5所示。

表5 编号对应关系

续表

运用杆组中拓扑结构信息和杆组拓展的邻接矩阵特征值和特征向量法进行同构判定，全程可由计算机完成，简单且实用。其中拓展的邻接矩阵在原有的邻接矩阵的基础上做出了拓展，增加了复铰以及外副的对应行列，使得矩阵中包含了更加全面的杆组结构信息。

4 结论

(1)通过对杆组拓扑图结构特点的分析，在邻接矩阵的基础之上提出了新的杆组拓扑图的描述方式——拓展邻接矩阵。该矩阵是能表示杆组构件、复铰、外接运动副之间的连接关系的对称矩阵，实现了杆组拓扑结构的唯一表示。

(2)综合了拓展邻接矩阵中包含的杆组各结构本身信息、它们之间的连接信息，以及杆组拓展邻接矩阵的特征值特征向量，给出一种杆组同构判定的新方法，特别是针对含复铰和外接运动副的杆组判定方法。该方法可完全由计算机来完成，是最简便操作方法之一。

(3)根据拓展邻接矩阵的行列变换，找出杆组中构件、复铰及外接运动副编号的对应关系，对杆组同构结果进行对比验证，由此提高了该判别方法的可靠性。