基于BP神经网络的异步电机转子磁链定向矢量复合控制*
2019-05-24李海侠林继灿符士宾张晖东
李海侠,林继灿,符士宾,张晖东
(桂林理工大学 机械与控制工程学院,广西 桂林 541000)
0 引言
异步电机成本低且性能可靠被广泛应用于工业中。基于解耦调速策略的转子磁场定向控制(Field-Oriented Control,FOC),又称矢量控制,不仅提高了转速可靠性和机械鲁棒性,同时还提供速度控制的快速动态响应[1]。
在异步电机矢量控制策略中,需要整定的参数受逆变器驱动电压、电机电流等影响,同时含有积分项,在给定输入的速度阶跃突变时,容易发生积分饱和而导致控制系统产生超调、增加系统步入稳定的时间。为此,许多新型控制策略被提出,文献[2]提出了使用PR调节器的策略,但不能为PR参数的整定提供很好的方法。文献[3] 中在永磁电机调速控制中使用IP控制器,并将电磁转矩量作为 IP 速度控制器的反馈补偿提高抗负载扰动能力,取得一定效果。文献[4]提出利用IITAE 的性能指标结合坐标轮换法来调整出PI 控制的参数值,但没有标准的规则来整定参数以及优化时间过长。文献[5]将扩展的卡尔曼滤波估计的转速应用于IP 控制器的转速控制,有效提高系统的抗负载能力,同时指出扩展卡尔曼滤波器(REKF)有效提高收敛能力。文献[6-7]提出了基于(Radial Basis Function Neural Network)RBF参数整定的调速控制方案,在RBF神经网络中,隐藏基函数的中心,隐射于输入样本中,难以反映出系统真正的输入输出关系。
本文提出基于反向传播 (Back Propagation)BP神经网络的异步电机矢量PI-IP复合控制策略,在定向矢量控制中,单一的PI控制器难以满足工程上对速度转矩精度要求较高的工作环境,将PI和IP控制器复合使用,形成PI-IP控制器,综合两者的优点,同时将具有非线性映射能力以及容错能力强的BP神经网络引入到矢量PI-IP控制中,自调整系统参数,实现矢量控制系统上速度环的复合控制,提高控制稳态精度,进而优化整定后的矢量控制系统。最后基于Simulink仿真平台,效验方法的可行性。
1 异步电机矢量控制

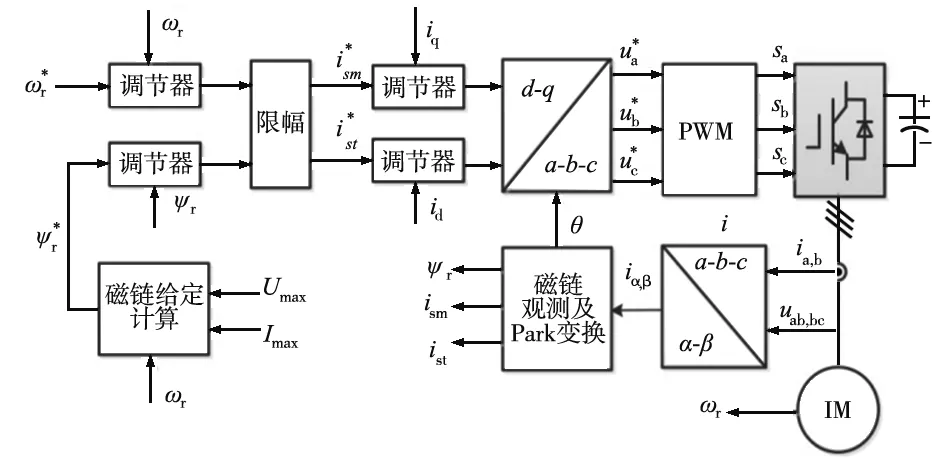
图1 异步电机矢量控制
转子磁链ψr的定向为控制系统的关键点,在mt坐标系上,转子磁链数学电流模型为:

(1)
式中,ω1为转子磁链旋转角速度,Lm为定子与转子同轴等效绕组间的互感,Tr转子电磁时间常数[9]。
电磁转矩mt坐标系下表达式为:
(2)
其中,pn为电机极对数。
2 BP神经网络的矢量PI-IP控制分析设计
BP神经网络,作为一种按误差逆向传播训练的自定义前馈网络,具有良好的自组织学习能力以及实现简单等被广泛应用于电力拖动领域当中。例如船舶推进电机故障预测分析,煤矿电机故障诊断预测,风力发电机绕组温度预测以及转子电机故障诊断预测等[10-13]。都取得较好的效果。
2.1 BP神经网络
BP神经网络隶属多层前馈网络,利用误差逆传播算法。影响因子系数利用最速下降法进行不停整改和学习,使误差平方和最小,结构框图如图2所示[14]。
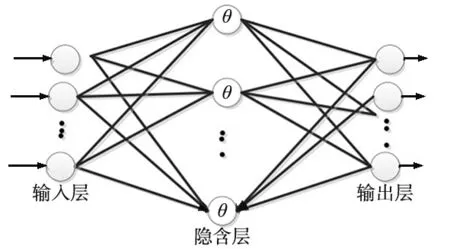
图2 BP神经网络结构图
2.2 转速闭环PI控制器分析
在异步电机系统中,从电机输出转矩差到转矩可以简化为一个积分环节,可表示为:
(3)
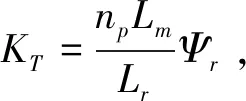
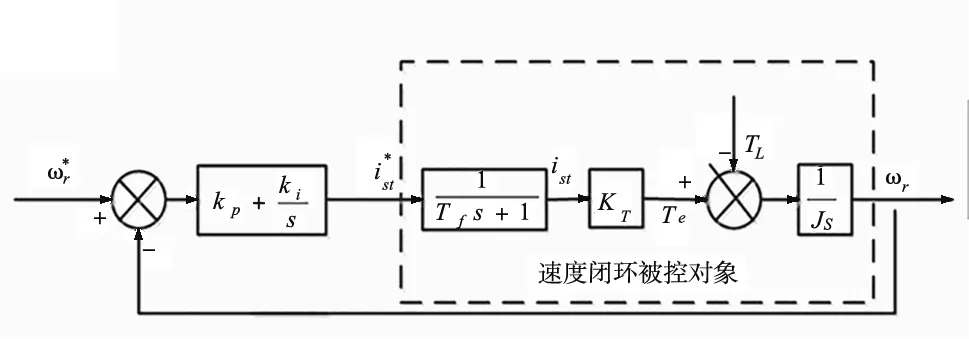
图3 异步电机转速环PI控制
(4)
(5)
分析式(4)和式(5)可知,负载介入如果急剧变化时,容易造成系统超调。在式(5)中也可以看出传递函数中分子微分项较大,所以速度给定信号为阶跃信号,容易引起速度超调和电流不稳。
2.3 转速闭环IP控制器分析
为减小速度环中参数微分项的影响,将比例环节移到反馈通道中可得IP控制器,结构图如图4所示。

图4 异步电机转速环IP控制
同样前提下可得控制器中的两个传递函数分别为:
(6)
(7)
分析式(5)和式(7)可知,PI和IP控制器具有同样特征方程,IP控制器传递函数中分子项少了KTKPs,也就是IP控制器可以有效减小速度环超调以及减少励磁电流的冲击电流。
为进一步分析两种控制器的工作性能,将电机参数表1代入式(5)和式(7),取KP=Ki=1,进行系统阶跃响应以及伯德图分析。

表1 电机参数表

图5 单位阶跃响应(PI和IP控制器对比)
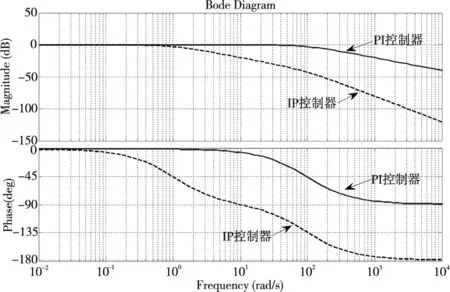
图6 系统伯德图(PI和IP控制器对比)
分析响应图和伯德图可得,IP控制器的超调量比PI控制器小,可减小励磁电流分量的冲击电流,但是采用 IP 控制比 PI控制器具有更大的相角滞后,跟踪响应不足,反应慢。
2.4 BP神经网络的速度PI-IP控制器
基于PI控制器和IP控制器在异步电机控制系统的分析,转速环传统 PI控制具有响应快、消除偏差能力强的优点,但容易引起超调量过大。IP控制器可以有效减少超调,但响应速度慢,跟踪性不足。为了更好的利用两种控制的优势,本文基于异步电机定向矢量控制上,转速环控制引入PI-IP复合控制,并增加转速因子在控制器上。PI-IP 复合控制策略参考文献[5]的原理框图,基于异步电机转速复合控制原理图如图 7 所示。其中,α为转速因子,变化范围0~1,当作为PI控制器时,α= 1; 当作为IP 控制器时,α= 0。

图7 异步电机PI-IP复合控制
PI-IP控制器采取增量式,变化误差根据转速为:
(3)
PI-IP控制器的离散形式:
(4)
BP神经网络中输入层的输入和输出分别为:
(5)
根据误差逆传播的思路,参数利用神经网络训练整定得出,设置输入层的输入为:
(6)
网络隐含层的输入输出为:
(7)
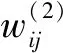
Δu(k)=u(k-1)+kp(e(k)-e(k-1))+kie(k)+
kd(e(k)-2e(k-1)+e(k-2))
(8)
PI-IP控制算法的输出为:
(9)
为简化等式,使kvki=kvi,kvα=kva,简化后等式为:
(10)
网络输出层的输入输出分别为:
(11)
速度环的控制指标为:
(12)
E(k)通过加权系数,进行反向下降整合,为提高搜索收敛效率,可以增加全局极小的惯性项。
(13)
等式中η为学习速率,β是惯性系数。
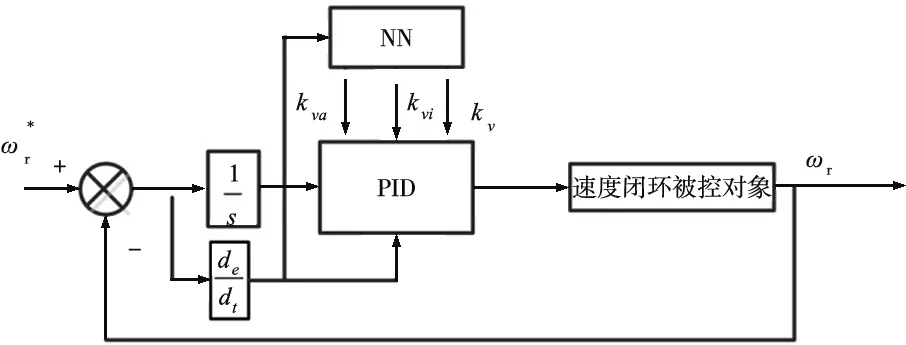
图8 BP神经网络PI-IP复合控制
(14)
加权系数的学习算法:

(15)
其中,

(16)
3 仿真分析
为了验证本文提出的BP神经网络的矢量速度 PI-IP 复合控制在异步电机调速系统中的可行性,在MATLAB/Simulink上进行仿真测试。仿真过程电机参数如上表1,BP神经网络中,网络层隐层神经元个数为5,初始值kv=20,kvi=0.025,kva=0.36,输出限幅范围[-20,20],给定采样周期取0.001s, 025s加入5N·m负载扰动。学习速率η=0.07,惯性系数β=0.5,仿真结果如图9~图11。
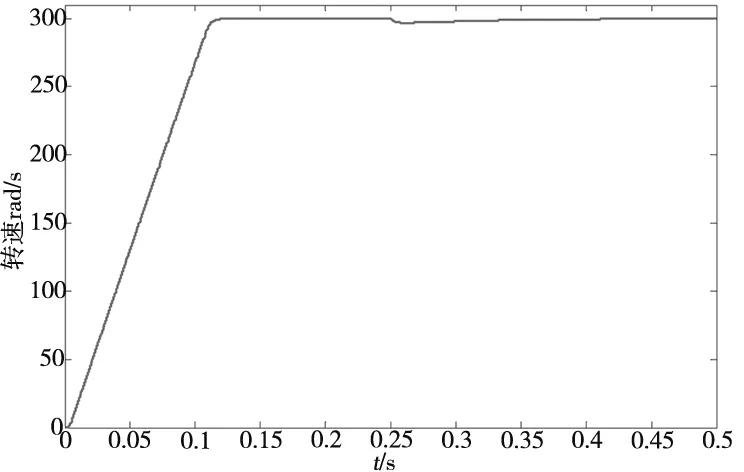
(a) 转速波形图
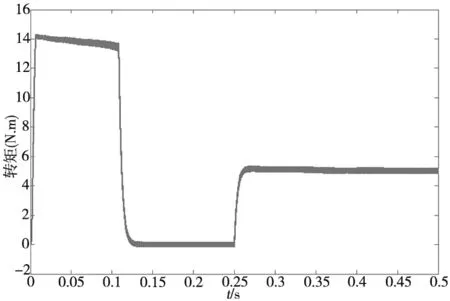
(b) 电磁转矩图图9 IP控制(α=0时)

(a) 转速波形图
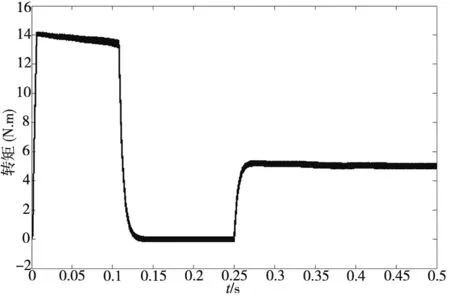
(b) 电磁转矩图图10 PI控制(α=1时)
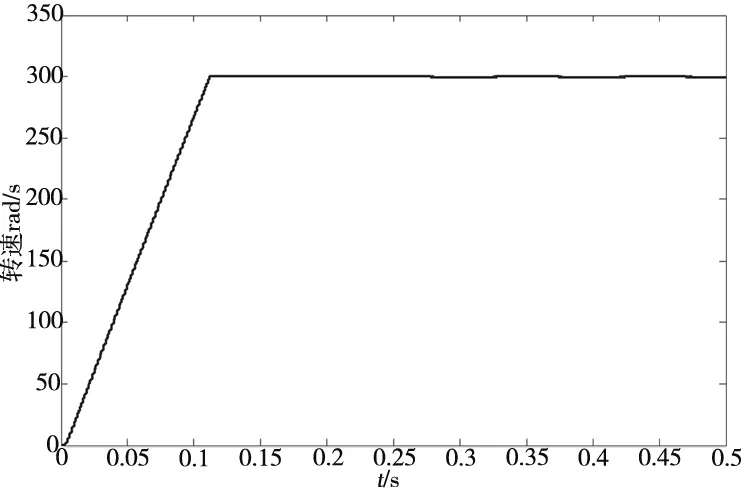
(a) 转速波形图
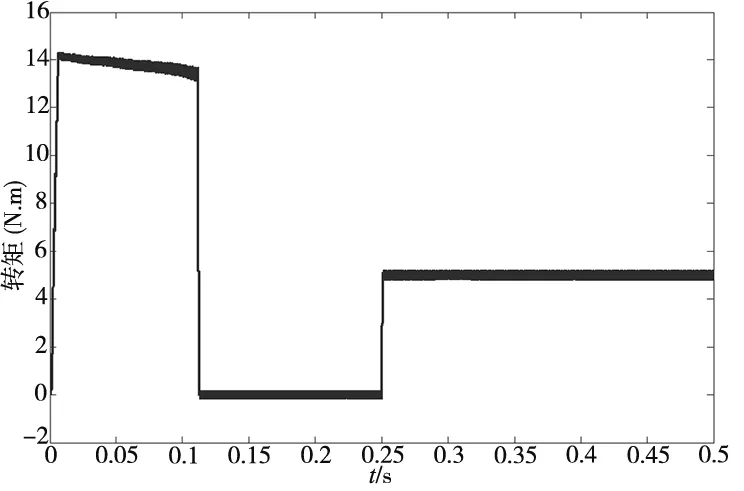
(b) 电磁转矩图
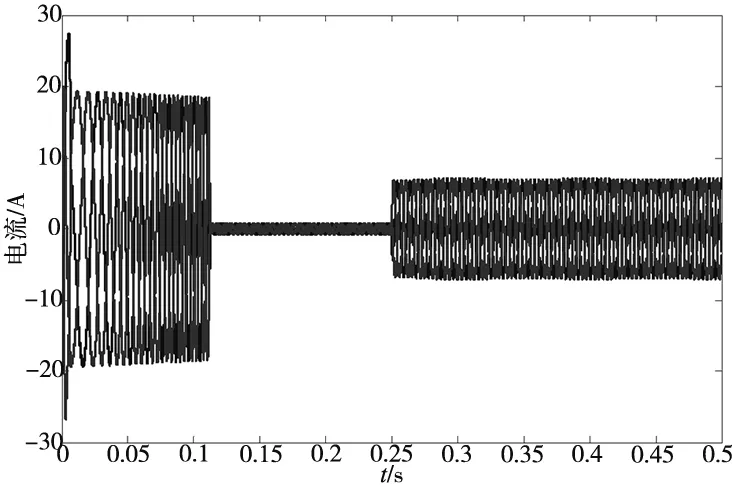
(c) 矢量速度PI-IP电流波形图
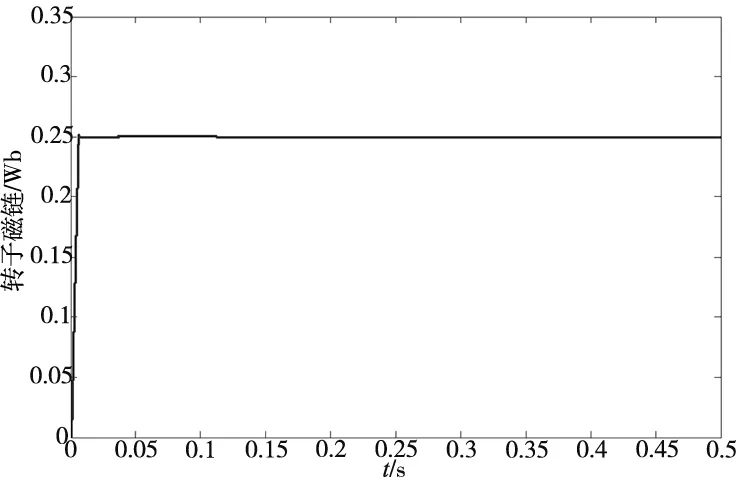
(d) 矢量速度PI-IP转子磁链波形图

(e) 控制参数自适应整定图11 BP神经网络PI-IP控制
分析图9~图11,常规PI控制策略中转速存在超调,稳定时间教长,常规的IP控制(α=0时)下转速跟踪响应不足,同样输入和输出给定值的情况下无法达到额定转速。而基于BP神经网络的矢量 PI-IP 控制策略转速响应优于传统控制策略,同时从转速和转矩波形图可看出系统稳健性优于传统控制策略。系统稳定后,0.25s加入负载扰动测试,通过输出曲线可知,与常规速度 PI 和 IP 控制方法相比,基于BP神经网络的矢量 PI-IP 控制策略能有效提高控制精准性,稳定时间更短,抗负载转矩扰动能力优于传统控制策略,抗负载扰动能力提升20%左右。综上可知,采用基于BP神经网络的矢量PI-IP 控制方法较常规矢量 PI 和 IP 两种控制方法而言,鲁棒性以及稳定性更优,电机的工作系统具有更好的动、静态性能。
4 结束语
本文转子磁链定向矢量控制策略与神经网络的PI-IP控制策略的相结合,给出一种基于建模调优的矢量PI-IP控制器,并在异步电机的调速系统中,验证方法的有效性。
同时,随着实时系统的变化,能够有效提高电机的工作性能,例如加入负载的情况下,电机能快速恢复稳定,并正常运行,以及算法实现过程的优化,能够降低系统的调节时间以及减小系统超调,提高系统的抗负载转矩扰动能力。
