改进ABC算法的串联机械臂多目标优化*

周 晟，孔建益，侯 宇，邹光明

(武汉科技大学 a.冶金装备及其控制教育部重点实验室；b.机械传动与制造工程湖北省重点实验室，武汉 430081)

0 引言

随着高速、高精度、自动化工业生产的不断推进，串联机械臂在航空航天，设备制造，产品装配等多项领域的应用也越来越广泛，对其在给定工作轨迹下的运行时间、能量消耗、脉动冲击等各项性能指标的要求也不断提高。因此，对串联机械臂进行工作轨迹进行优化设计，以此缩短生产时间、减少能量消耗、提高工作效率、降低运行过程中产生的脉动冲击、延长零部件使用寿命具有十分重要的意义，亦是现代机械臂研究重要的方向。

国内外学者针对轨迹优化进行了广泛而深入的研究，管成等引入矢值函数，运用莱布尼茨公式对5次NURBS曲线进行高阶求导[1]。分析了NURBS曲线因子对轨迹规划的正向作用，能够有效减少能耗，增强工作轨迹的平滑性。孙亮等采用基本样条插值法，对运行轨迹进行优化设计，降低脉动冲击，从而提高运行的平稳性[2]。但上述研究均未提出算法进行优化，其优化结果局限于局部最优而未达到全局最优。喻骁等采用粒子群算法对响应指标进行单目标优化，未考虑多目标优化时，各项性能指标之间的关联性[3]。

文中在上述研究基础上，结合改进人工蜂群算法，以串联机械臂运行时间、能量消耗和脉动冲击为目标建立目标函数，利用五次NURBS曲线对运行轨迹进行插值优化，构建通过指定关节位置点且加加速度连续的关节轨迹曲线。通过改进人工蜂群算法实现多目标轨迹优化，求解Pareto最优解集，构造归一化权重目标函数，获得满足约束条件的最优解及相应运行轨迹。取PUMA560串联机械臂为对象，设定相关参数进行仿真分析，验证算法的有效性。上述研究能有效提高串联机械臂整体工作指标，对现代化生产能力的提高具有重要意义。

1 轨迹规划及目标函数构造

1.1 基于NURBS曲线的轨迹规划

针对给定工作轨迹，选取其所在任务空间，对空间内整体轨迹进行离散化处理[4]。通过运动学反解，求取优化分析所需的理论关节点pji=(qji,ti),其中j=1,2…n，i=1,2…m，n为机械臂关节数，m为关键路径点数，qji为关节j在点i处的角度值，ti为该处时间。将串联机械臂轨迹规划问题进行转化，表示为构造满足约束条件的轨迹方程，运用k次NURBS曲线理论构建串联机械臂运行轨迹数学模型：

(1)

式中,设定u时刻关节位置为P(u)；ωi为NURBS曲线权因子；Di为NURBS曲线控制顶点；Ni,k为通过节点矢量U定义的u向k次B样条有理基函数，其中U={a…auk+1…um-k-1b…b}

为满足首末控制顶点均由构造出的NURBS曲线经过，设定a=0,b=1，全部i,ωi>0,且设定：

(2)

根据等式(2)将等式(1)转换为：

(3)

式中，Ri,k(u)为有理基函数，采用函数表达式Ri,k(u)表示u∈[0,1]区间内的分段有理函数。

根据等式(3)可得：

(4)

式中，A(u)为矢值函数，运用Leibniz formula对A(u)进行P(u)的高阶导矢函数表达式求导计算，可得：

(5)

根据等式(5)可得：

(6)

采用等式(6)可计算出对P(u)进行k阶导矢函数表达式的计算结果。

根据5次NURBS轨迹规划理论，关节曲线需经过规划问题中指定的关节位置点，以此选取经过指定关节位置点控制顶点的NURBS曲线，由此可得：

(7)

式中，i=0,1,2…,n，以n表示指定关节位置数；Dj表示NURBS曲线上的n+k个控制顶点；k表示NURBS曲线的次数；j=0,1,2…,n+k-1。

根据串联机械臂末端执行器,5次NURBS曲线关节轨迹函数式及实际工况，设置4个约束条件，由此可得n+5个轨迹约束方程：

(8)

式中，vs、as为串联机械臂各关节起始速度和加速度；ve、ae为串联机械臂各关节停止速度和加速度，依据实际工况设定其参数数值。根据控制顶点Dj、权因子ωj和时间点u等各项参数，即可构建通过指定位置，且加加速度连续的关节轨迹曲线。

1.2 目标函数构造

生产中为满足工业化需求，对串联机械臂工作状态下的运行时间、能量消耗和脉动冲击等关键性能指标进行详细分析，对所需优化的目标函数及约束条件进行如下规定：

位置约束：|qji(t)|≤Qjmax

(9)

式中，S1为路径总时间，是各路径点之间运行时间间隔之和，以此对串联机械臂整体运行时间进行有效衡量；S2为工作状态下运行加速度，以此对机械臂能耗指标进行有效衡量；S3为工作状态下运行轨迹加加速度值，以此对串联机械臂脉动冲击进行有效衡量；Qjmax、Vjmax、Ajmax、Jjmax为相应关节位移、速度、加速度和加加速度的最大值。

2 算法原理及步骤

2.1 标准人工蜂群算法

人工蜂群算法是一种依据蜜蜂种群采蜜的生物行为，所研究出的群智能优化算法。该算法中的蜂群整体由采蜜蜂、旁观蜂和侦查蜂三种类型组成，将蜜蜂寻找蜜源过程抽象为寻找问题最优解过程[5-7]。

首先，ABC算法在D维解空间内随机产生N个初始蜜源xi=(xi1,xi2…xiD)，采蜜蜂根据等式(10)在蜜源附近进行全局搜索。

vij=xij+R(xij-xkj)

(10)

式中，k∈{1,2,…N}，j∈{1,2,…D}，k，j均为随机值且满足j≠i；通过R∈[-1,1]实现对邻域范围的控制。

假设搜索到的新蜜源适应度值高于旧蜜源，则以新蜜源位置代替旧蜜源位置，否则保持不变。当所有采蜜蜂完成搜索后，返回交流区通过摇摆舞将蜜源信息分享给旁观蜂。旁观蜂获取信息后，根据贪婪选择策略依等式(11)计算所得概率值对蜜源进行选择。

(11)

式中，pi为第i个蜜源的选择概率值；fitni为第i个蜜源的适应度值；fi为所需优化问题的目标函数。

假定采蜜蜂经过limit次尝试后仍未提高解的质量，则采蜜蜂角色转变为侦查蜂，且侦查蜂依据等式(12)随机产生一个新解代替原来的解。

xij=xmin,j+rand(0,1)(xmax,j-xmin,j)

(12)

式中，xij为第i个解的第j维分量；xmax,j，xmin,j分别为解的最大值及最小值；rand(0,1)为[0,1]内随机值。

2.2 改进人工蜂群算法

标准ABC算法在进行目标函数优化时易局限于局部最优、收敛速度较慢等缺陷，为弥补上述缺陷对局部搜索策略进行一定改进，据此提出一种基于改进局部搜索策略的ABC算法。研究发现混沌局部搜索在面对较小的搜索空间时具有高效的搜索寻优能力，因此在进行空间搜索时，旁观蜂以当前最优解的混沌局部搜索策略进行寻优操作。

首先，依据Logistic生成混沌序列[8]：

Ci+1=4·Ci·(1-Ci)

(13)

式中，i∈{1,2,…M}；Ci∈[0,1]且Ci≠0,0.25,0.50,0.75,1.00；M为混沌序列长度。

利用等式(14)求取具有混沌性质的蜜源当前位置chxij：

chxij=Cj·xij

(14)

式中，xij为第i个解的第j维分量；Cj为混沌序列的第j维分量。

利用等式(15)求取新蜜源位置：

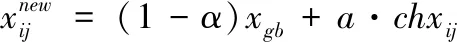
(15)

式中，xgb为当前最优解；a为缩放因子；itx为当前迭代次数；MCN为最大迭代次数。

为提高ABC算法收敛精度与速度，有效避免解的随机性，并使其局部搜索范围随着迭代次数上升而逐渐减少，提高算法局部搜索能力，侦查蜂采用当前最优解的自适应侦查策略，如式(16)所示[9-10]。

(16)

2.3 改进人工蜂群算法基本步骤

改进算法流程图如图1所示，算法基本步骤如下：

Step 1：蜜源xi初始化，设定最大迭代次数、混沌序列长度等基本参数；

Step 2：采蜜蜂依据等式(10)依次在每个蜜源附近进行搜索，对比新旧蜜源的适应度值；如果新蜜源适应度值较大则更换蜜源位置，否则不变；

Step 3：选取当前最优蜜源信息，提供给等式(15)进行计算；

Step 4：依据等式(11)计算每个蜜源被选择的概率，旁观蜂依据贪婪选择策略选取蜜源，按照等式(15)进行搜索。

Step 5：如果搜索次数达到最大迭代次数limit且未更新，则侦查蜂按照等式(16)在当前最优蜜源周围，随机产生一个新的蜜源位置。

Step 6：对当前最优解进行记录。

Step 7：对迭代次数进行判断，是否已达到最大迭代次数MCN，若达到则输出最优解，否则转到Step2进入循环。

图1 改进人工蜂群算法流程图

3 仿真分析

通过具有普适性的PUMA560串联机械臂对算法进行分析验证，设定串联机械臂工作轨迹，对串联机械臂完成规定任务的各项参数进行优化设计，使其优化结果在满足实际工况的同时趋于全局最优。

3.1 机械臂建模

绘制串联机械臂连杆模型图，按照D-H约定在图中建立关节坐标系，其结果如图2所示。通过串联机械臂运动学理论获取D-H参数，如表1所示，依据表1求解出串联机械臂正、逆解函数表达式。

图2 关节坐标系

序号aiαidiθi10-900θ1200d2θ23a200θ34a30d4θ450-900θ560900θ6

表1中，αi表示为连杆扭曲；ai表示为连杆长度；di表示为连杆偏置；θi表示为关节转角。

通过Ai矩阵所描述的齐次变换关系与D-H约定得到连杆变换等式：

(17)

式中,Cθi=cosθi；Sai=sinai；Sθi=sinθi；Cai=cosai；C-1θi=cos-1θi；S-1θi=sin-1θi；将表1数据带入连杆变通式后，得到相应的齐次变换矩阵等式：

(18)

根据等式，求解相应运动学正向模型如等式(19)～式(21)所示。

px=c1·[a2·c2+a3·c23-d4·s23]-d2·s1

(19)

py=s1·[a2·c2+a3·c23-d4·s23]+d2·c1

(20)

pz=-a3·s23-a2·s2-d4·c23

(21)

运用仿真软件根据表1构建串联机械臂模型，如图3所示。

图3 运动学模型

3.2 参数设置

仿真对象PUMA560串联机械臂各关节运动限制参数如表2所示，各关节运行轨迹采用五次NURBS曲线进行构建，为贴近实际工况设定启动、停止时刻的速度值、加速度值均为0。设定改进人工蜂群算法最大迭代次数100，维数为30，蜜源、采蜜蜂和旁观蜂数目均为50，阈值参数limit=100。

表2 运动学约束

4 仿真结果分析

根据改进人工蜂群算法，求解出轨迹运行时间、能量消耗和脉动冲击均趋于最优的多目标优化Pareto前沿面，如图4所示。根据图示信息可知，能量消耗性能指标与脉动冲击性能指标表现为正向相关，与整体运行时间性能指标趋于负相关。

图4 Pareto解集示意图

为满足实际要求，构造归一化权重目标函数如式(28)所示，在Pareto解集中选取全局最优且满足约束条件的最优解。

(28)

式中，设定N1，N2，N3为实现各目标函数处于同一范围，α1，α2，α3为根据实际工况需求，所设定的各目标函数值所占的权重系数，对等式(28)进行最小化求解，即可获取所需最优解。

图5 各关节位移曲线

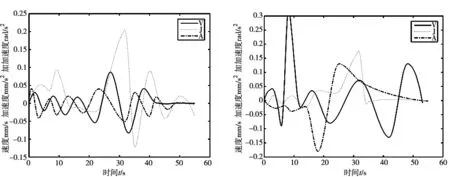
(a) 关节1速度、加速度及加加速度 (b) 关节2速度、加速度及加加速度

(c) 关节3速度、加速度及加加速度 (d) 关节4速度、加速度及加加速度

(e) 关节5速度、加速度及加加速度 (f) 关节6速度、加速度及加加速度图6 各关节速度、加速度及加加速度曲线

5 结论

(1)针对串联机械臂多目标轨迹规划问题，利用5次NURBS曲线对运行轨迹进行优化分析，有效减小插值计算过程中表达式初始计算的误差值。

(2)提出改进人工蜂群算法，该算法收敛速度较快、搜索空间较广。其中旁观蜂以当前最优解的混沌局部搜索策略进行寻优操作，在面对较小的搜索空间时具有高效的搜索寻优能力。侦查蜂采用当前最优解的自适应侦查策略，提高算法收敛精度与速度。

(3)选用PUMA560串联机械臂，以其整体工作时间、能量消耗和脉动冲击为优化目标建立目标函数并对其进行多目标优化设计。验证了算法的有效性，提高串联机械臂的整体工作性能，为后续研究与分析奠定理论基础。