Parametric study of single con f i ned fragment launch explosive device
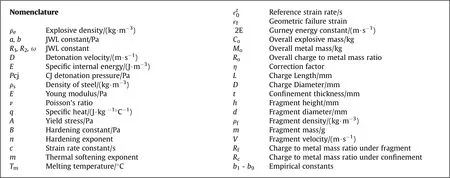
2019-05-24PnkjChoudhKumrswmyKusumkntDhote
Pnkj K.Choudh ,A.Kumrswmy ,Kusumknt D.Dhote
a Armament Research&Development Establishment(DRDO),Pune 411021,India
b Defence Institute of Advanced Technology,Girinagar,Pune 411025,India
Keywords:Con f i nement Fragment size Empirical relationship Fragment velocity Insensitive munition test Fragment launching device
A B S T R A C TIn this article,parametric study of single con f i ned fragment launch device w as carried out.The con f i guration proposed w as further studied to derive the empirical relationship for effect of fragment size,charge size,con f i nement thickness on fragment velocity.The simulations were carried out using ANSYSAUTODYNE explicit solver.Fragment velocities w ere estimated as a function of different parametric combinations of explosive quantities,charge length to diameter ratio,fragment height to diameter ratio,con f i nement thickness,fragment material and fragment mass.The data was further converted to charge to metal ratio under fragment and con f i nement.It w as observed that,increase in con f i nement thickness,charge quantity and decrease in fragment height increases the fragment velocity.It is also noted that,charge to metal mass ratio under fragment signi f i cantly affects the fragment velocity.At the end,an empirical relationship for fragment velocity interms of all these parameters was established.Using these relations,two velocities 1831.92 m/s and 2523.9 m/s required for NATO STANAG 4496 IM test were estimated.The design parameters for these velocities are presented.Also,the results estimated using the empirical relationship has been compared w ith published experimental data.Error in the predicted velocities is w ithin the acceptable range.The empirical relationship proposed w ill be useful for f i nalization of design of the fragment launch device.
1.Introduction
Impact physics and terminal ballistics are the important areas of military applications.Launching of fragment and consequent study of damage is a requirement in the evaluation of storage safety of ammunitions.NATO STANAG 4496 test for insensitive munition(IM)compliance requires launch of cylindrical fragment of 18.6 g mass and 14.3 mm diameter for primary and alternate test methods at velocities 2530 and 1830 m/s respectively[1].Test requirements for testing personal armours as per NATOSTANAG-2920 for ballistic test method for personal armour materials and combat clothing requires launch of fragments w eighing betw een 0.13 g and 53.78 g at striking velocities betw een 198 m/s and 1524 m/s[2].To meet these test requirements and assessing the performance,projectile or fragment launch devices capable of launching the fragment of desired mass and shape at speci f i ed velocity is essential.
To launch the projectile or fragment in a w ide range of velocities,electromagnetic propulsions,explosive propulsions,plasma accelerators and gun accelerators are available.Among all these techniques,explosive launch devicesare simple in construction and inexpensive.Large masses in the kilogram regime can be accelerated at high velocities of the order of 6 km/s[3].Techniques other than explosive propulsion are not feasible to carry out limited amount of studies w ithin limited cost.Further,safety of these equipments is essential during the test.Larger safety distances beyond 3m may be required to carry out these test on large size w arheads.In such tests,explosive propulsion or acceleration based techniquesare preferred.Wenzel[4]and Held[5]review ed different types of explosive launch devices used for f i ring of preformed fragments w ith launch velocities,launch masses,their scalability and limitation.These devices can also be used for launching of fragments formed during the f l ight after detonation of explosive i.e.P-charge,shape charge fragments.
The launch velocity of these fragments depends on the type of phenomenon used for launch.P-charge generator for individual and multiple fragments are capable of projecting heavier fragments at velocities of 3 km/s[5].Flyer plate studies have been done by many authors.Seokbin[6]has discussed the method for obtaining the acceleration pro f i le of f l yer plate.Yadav et al.[7]have reported f l yer plate experiments and brought out that the f l ying velocity increases w ith increase in charge to metal mass ratio.Weickert et al.[8]have performed parametric experiments using various diameter charges of different explosives for f l at plate launch.It w as con f i rmed that the plate velocity is a function of the plate thickness.Joseph et al.[9]have derived correlations betw een plate thickness and charge length for f l yer plate velocity.
Theoretical estimate of velocity for multiple fragments for cylindrical,spherical and sandw ich con f i gurations are given based on Gurney equation[10].The acceleration of individual fragments in different contact spacing w ith explosive is discussed in detail[11].The method of estimating velocity of multiple premade fragments in forward f i ring con f i guration is also presented[12,13].In case of a cylindrical charge consisting of fragmenting disc at one end w ith initiation at the other end,the modi f i ed Gurney equation w ith charge length to diameter effect w as used for obtaining the fragment velocity[14].
Wenzel[4]has presented single fragment launch con f i guration w ith different type of pellets i.e.spherical,disc w ith annular con f i nement,plate,disc w ith air cavity etc.It w as brought out that,the velocity of pellet can be enhanced by f i xing the pellet mass and increasing the explosive mass,w hich is initially linear,however becomes asymptotic once the detonation front reaches the detonation velocity.Further,tw o con f i gurations i.e.disc w ithout con f i nement and disc w ith annular con f i nement have been experimentally evaluated by Held[15,18].Held suggested that,a single fragment w ithout annular con f i nement cannot be accelerated w ell.In addition,the release waves reduce the high pressure zone rapidly after the fragment launch.Therefore,only moderate velocities are achieved w ith uncon f i ned fragment launch.Further,w ith this con f i guration,a w ell predicted mass and shape cannot be achieved.Con f i guration of disc w ith annular con f i nement has achieved reproducible fragment velocities and the fragments have suf f i cient aiming accuracy w ith only small fragment deformation by the detonative acceleration.Therefore,disc launch w ith annular con f i nement has de f i nite advantages.
Launch velocity of single con f i ned fragment launch explosive device(SCFLED)considered in the present study depends on various con f i guration parameters.The launch velocity of fragment is dif f i cult to be estimated theoretically,w hen con f i nement and fragment height are different.Gurney equation provides an average fragment velocity based on overall con f i guration i.e.overall charge to metal mass ratio,therefore,the effect of fragment dimensions w ithout change of con f i nement dimensions cannot be captured.Effortshave been made in similar linesto further modify the gurney equations or propose empirical relationships for estimation of fragment velocity for non-conventional designs[16,17].
Careful observation of above literature data indicates that,the general expressions are available for calculation of average fragment velocity of natural fragmentation or preformed multiple fragmentation devices used for forw ard f i ring w arhead applications.However,method of calculation of fragment velocity for single fragment launch devices is not available in the literature.Therefore,the present study has been focused speci f i cally to understand the effect of con f i guration parameters on single fragment launch velocity in SCFLED proposed by Held[18].The data generated from simulation w as used to obtain the generalized relation required to design these devices.The design parameters of these devices for NATO STANAG 4496 test for insensitive munition(IM)compliance has been estimated using generalized relations.
The launch velocities of 10 g and 20 g masses of disc fragments w ith annular con f i nements have been studied.Effect of changes in the charge to metal mass ratio of overall con f i guration w ith f i xed explosive quantities,fragment length to diameter ratio,front con f i nement thickness and change of fragment material have been studied for fragment launch velocities.After conducting the simulations studies,empirical relationship for above parameters has been proposed.The relationship w as further veri f i ed for fragment velocity of 12 g and 24 g masses w ith reported experimental results.The errors of estimation are w ithin the permissible limits.Thus,the empirical relationship established in this study can be utilized for w orking out the con f i guration for desired mass and launch velocity of fragment.
2.Numerical modelling
ANSYS-AUTODYN software has been used for numerical modelling of SCFLED.The Held con f i guration w as f i rst modelled in 3D quarter symmetry.It involves Jones,Wilkins and Lee(JWL)equation of state for explosive and Johnson cook(JC)high strainrate behaviour of mild steel for con f i nement material.The explosive material w as modelled using Euler domain.The con f i nement and fragment w as modelled using Lagrange domain.
2.1.Geometry details
In Held con f i guration,the fragment is positioned at the centre of con f i nement at one end of cylindrical explosive charge and detonated from the other end as show n in Fig.1(a).The fragment is con f i ned w ith front con f i nement thickness t equal to fragment height h.The proposed con f i guration hasφ96×95 mm.The values of d and h w ere selected in such a w ay that,the mass of fragment is either 10 g or 20 g and the angle of front con f i nement w ith charge is chosen as 100°.For the parametric study,geometry of launch device w as further simpli f i ed as show n in Fig.1(b)in w hich front con f i nement was changed to 90°.The con f i nement w as modi f i ed at the fragment holding location w ith 45°taper as discussed in the subsequent sections.
2.2.Material models
The RDX/WAX/Graphite(94.5/4.5/1)w as used as explosive material in the experimental study.JWL equation of state given in Equation(1)w as used for modelling of explosive,w hich describes the detonation product expansion for high energy explosive materials.JWLparameters for the explosive are given in Table 1.
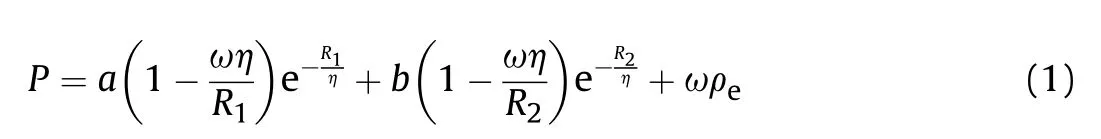
The mild steel was considered for con f i nement and fragment material and J-Cmaterial model considered is given in Equation(2).Properties for mild steel involved in analysis are given in Table 2 and Table 3.Whereε·t=
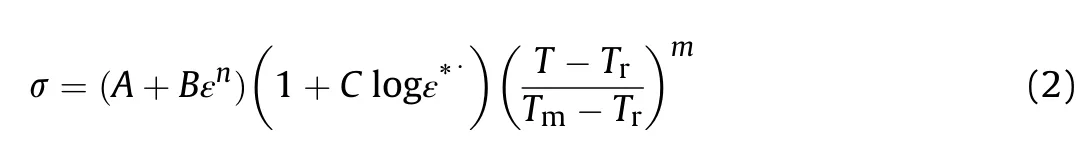
3.Results and discussion
3.1.Validation of numerical model
In 3-D quarter symmetry model used in the present study,the mesh size of 1 mm for explosive,1 mm for con f i nement and 0.25 mm for fragment w ere f i nalized after convergence study for fragment velocity.The simulation was carried out for 5 ms duration to obtain the maximum velocity.The numerical results are validated by experimental data generated by Held[18]for 10 g and 20 g fragment mass.For a given explosive,the key parametersgoverning the fragment velocity are E,Ro=Co/Moand L/D ratio of the explosive charge.The fragment velocity is calculated using modi f i ed Gurney Equation(3)w ith a velocity correction factorηof 0.9[12].The comparative results reveal that,the%error in simulation in comparison w ith experimental results is w ithin the acceptable limit as given in Table 4.
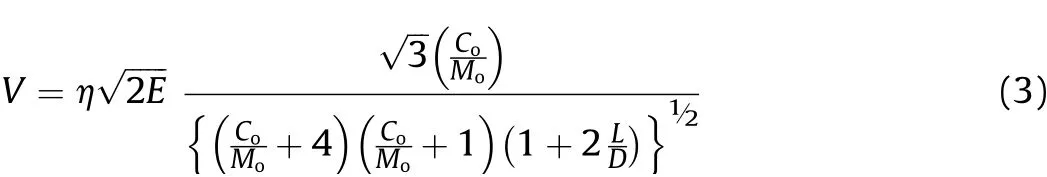
Gurney equation is used for fragmenting disc w ith multiple fragments.The average fragment velocity for con f i guration is estimated based on Ro.When fragment size is changed w ithout changing the mass of fragment keeping con f i nement thickness constant,the overall Row ill not change.In such cases,Gurney Equation(3)cannot predict the change in fragment velocity.In view of the above,there is a need to establish new empirical relationship for better correlation betw een size of fragment,charge and con f i nement dimensions.
Subsequent to the above validation,further simpli f i cations w ere made for parametric studies i.e.fragment w as considered rigid and front con f i nement angle w as changed to 90°.The validation of fragment velocity for both the massesrevealed that,there is a slight increase in the velocity of fragment due to change in con f i nement charge angle,w hich in turn increased the mass of explosive.Therefore,rigid fragment and 900con f i nement angle w as considered for all further simulation study.
3.2.Parametric study of SCFLED
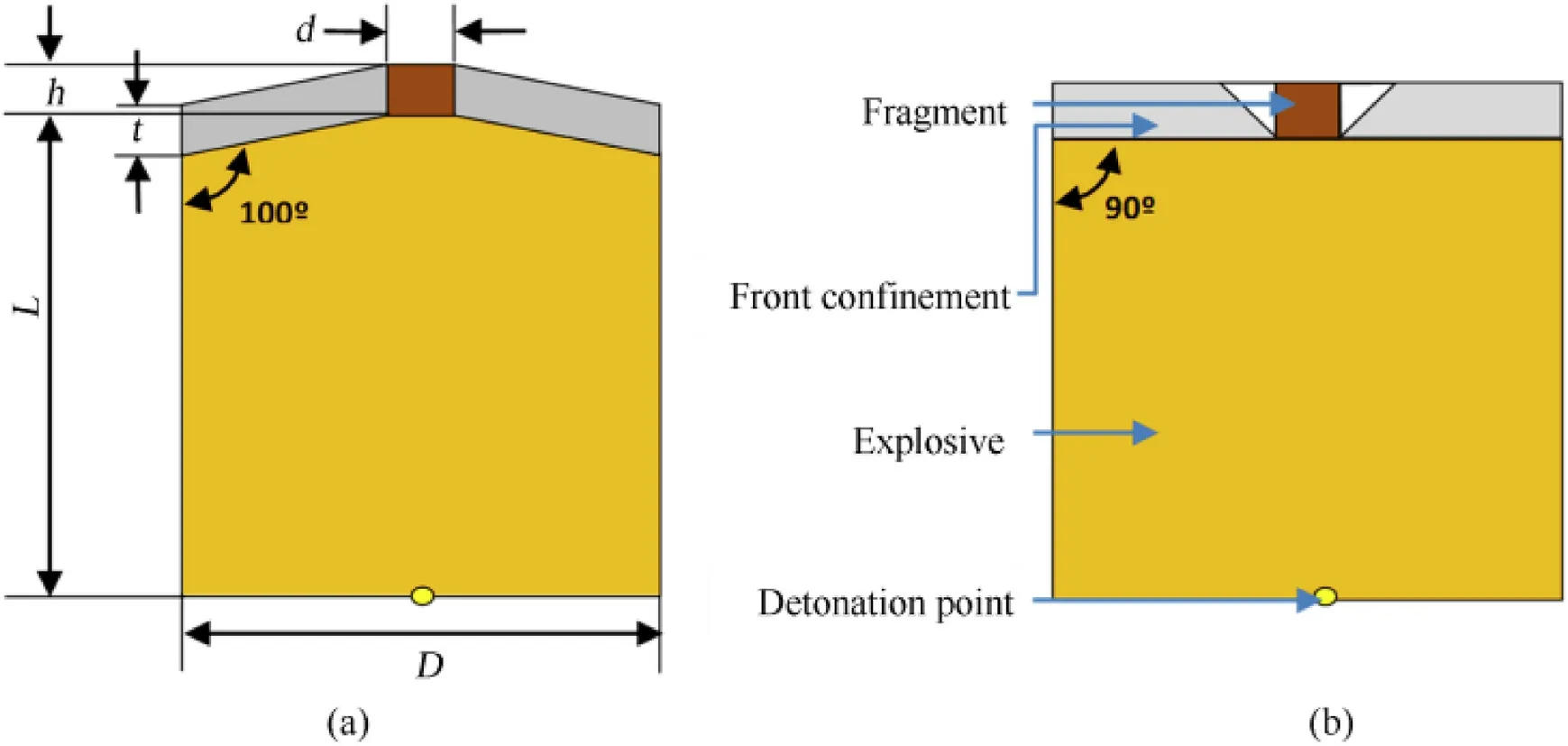
Fig.1.(a)Held con f i guration(b)Simpli f i ed SCFLED for parametric study.
The simpli f i ed geometry show n in Fig.1(b)w as used for parametric study.It is necessary to establish dependence of various parameters of SCFLED on the fragment velocity,w hich w ill help in f i nalization of SCFLED design.The single point initiation was considered at the centre of f l at end on the other side.Varying the s at L/D=1,Ro=1.2 and then it started decreasing due to rarefaction w ave and dominating end effects.For L/D>1.0,larger Row ill not help in further increase in the fragment velocity.Further,as the explosive charge quantity is increased,the maximum velocity of geometric parameters keeping the material parameters for explosive,frontal and radial con f i nement f i xed,the effect of these parameters on fragment velocity w as studied.The parameters used during simulations are given in Table 5.

Table 1JWL material parameters for RDX/WAX/Graphite(94.5/4.5/1).

Table 2Material properties for mild steel.

Table 3J-CMaterial parameters for mild steel[19].

Table 4Fragment velocity for different fragment mass obtained from simulations and errors.
3.2.1.Effect of length and diameter of explosive
Tw o fragment masses of 10 g (φ12.75×10)and 20 g(φ15.8×13),same front con f i nement and charge diameter,thickness of con f i nement equal to fragment height w ere considered in the simulation.D w as increased from 83 to 314 mm,L w as increased from 60 to 360 mm and charge quantity w as varied from 0.54 to 20.23 kg L/D ratio of charge w as varied from 0.5 to 1.75for f i xed quantity of charge(Co).Variation of maximum fragment velocity as a function of L/D ratio at different charge quantities obtained from simulations is plotted in Fig.2(a)and values are given in Table 6.
The effects of Ro on fragment velocity for various L/D ratios have been plotted in Fig.2(b).In case of 10 g fragment,for small quantity of explosive charge i.e.0.54 kg,as the L/D ratio is increased,Ro increased from 1 to 7.63.Fragment velocity increased to a maximum value of 1091 m/s at L/D=1,Ro=1.54 and thereafter it w as observed to be decreasing.As the explosive charge quantity is increased,the maximum velocity of fragment Vmax=2252 m/s w ill shift from L/D=1 to 1.25 at Ro=6.1.
On the other hand,in case of 20 g fragment,as the L/D ratio is increased,Ro increased from 1 to 5.87 for same explosive charge of 0.54 kg.Fragment velocity increased to a maximum value of 881 m/fragment 2252 m/s w ill shift from L/D=1 to 1.5 at Ro=5.3 for 20.54 kg explosive.

Table 5Parameters used in simulations.
It is also observed that,increasing the explosive quantity w ill increase the fragment velocity as seen in Fig.2(b).Overlapping of plots for 10 g and 20 g fragment mass indicates that,the fragment velocity issame at all valuesof Ro.Hence,charge to metal massratio dominated by con f i nement thickness and explosive height under con f i nement affects the maximum fragment velocity.
3.2.2.Effect of fragment height,diameter and material
The fragment velocity as a function of different fragment parameters such as fragment height,diameter and material w as obtained for tw o fragments of mass 10 g and 20 g.Explosive dimensions ofφ96×95 mm gives rise to a mass of 1.13 kg.The thickness of front con f i nement varied from 1.5 to 15 mm,the fragment h/d ratio w as also varied keeping the fragment mass constant for each con f i nement thickness.The density of aluminium w as considered 2.71×103kg/m3.During the simulation,it w as observed that,w hen fragment height is less than con f i nement thickness as show n in Fig.3(a),the fragment w ill start moving due to shock pressure.Subsequently,shock in con f i nement travel faster and reaches the free surface ahead of the fragment causing con f i nement material to f l ow over the fragment restricting its motion as show n in Fig.3(b).To overcome this problem,con f i nement w as provided w ith the angle of 45°from the base to outside the con f i nement as show n in Fig.1(b).
The effect of con f i nement t/L ratio w ith change in fragment h/d and h/L ratio on fragment velocity are plotted in Fig.4(a)and Fig.4(b)respectively and given in Table 7.For 20 g fragment,it w as observed that,the fragment velocity is 469.9 m/s at t/L=0.01316 and h/d=1.66 increased sharply to 1551 m/s w ith decrease in h/d ratio to 0.2346.Further,increasing t/L to 0.158 w ill increase fragment velocity to 668.7 m/s.It may be noted that,the fragment velocity increased w ith increase in front con f i nement and decrease in h/d ratio.It is also observed that,fragment velocity is independent of fragment mass of same material,h/L and t/L as show n in Fig.4(b).The h/L ratio has indirect bearing on Rfratio under the fragment.of these parameters.It w as observed that,w hen L/D ratio of charge is varied,the overall Rois governed by con f i nement mass or thickness.Further,study of fragment velocities for different h/d ratios and fragment material revealed the effect of charge to metal ratio under the fragment(Rf).Therefore,parameters w ere further converted to charge to m etal mass ratio under fragment Rfand under con f i nement Rcas de f i ned in Equation(4)and Equation(5).All the parameters w ere correlated to fragment
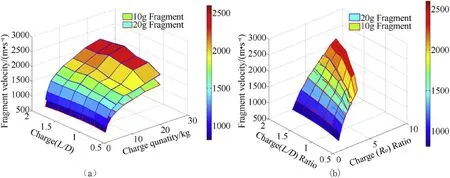
Fig.2.(a).Fragment velocity vs.L/D and C o(b)Fragment velocity vs.L/D and R o.
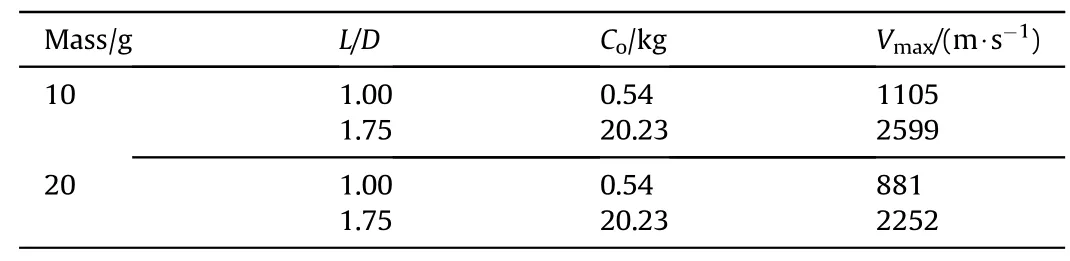
Table 6Variation of V max w ith L/D and charge quantity(C0).

Fig.3.(a)Fragment height less than con f i nement(b)Obstruction by Con f i nement.
Simulations w ere further carried out for Al fragment and results w ere compared w ith steel fragment of 10 g and 20 g fragments as shown in Fig.5 Since the density of Al is less than steel,fragment dimensions and fragment velocity of Al are higher.Therefore,for same h/L ratio,the charge to metal ratio under fragment(Rf)for Al fragment w ill be higher con f i rming that fragment velocity is a function of Rf.
4.Analysis of data and em p irical relationship
The data w as analysed after obtaining the individual variation velocity using the MATLAB program.

The empirical relationship correlating charge L/D,Rfand Rcwas established and given in Equation(6).This equation can be used to estimate fragment velocity,V for the given con f i guration and for f i nalization of SCFLED dimensions.
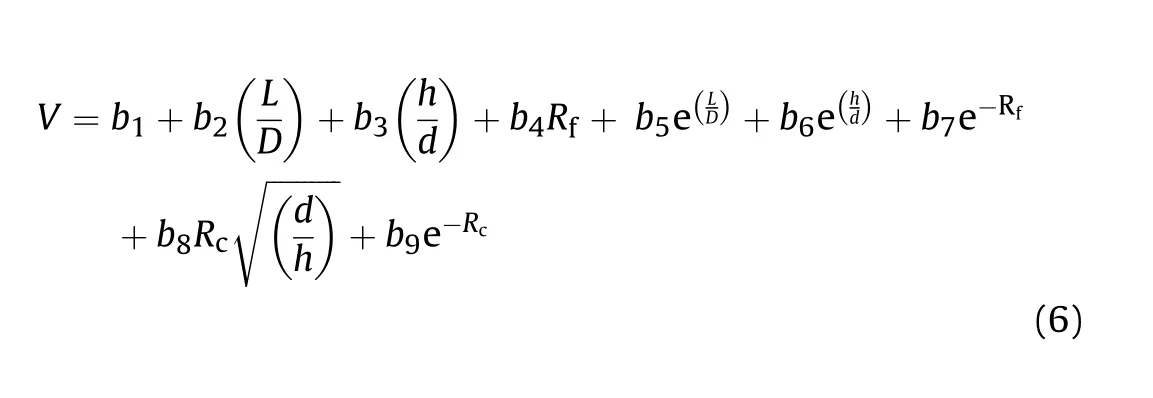
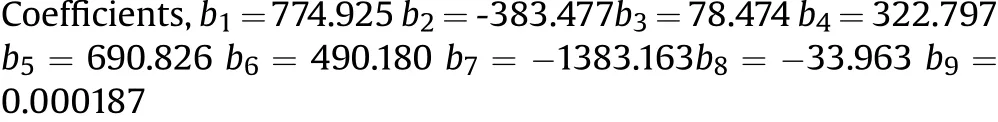
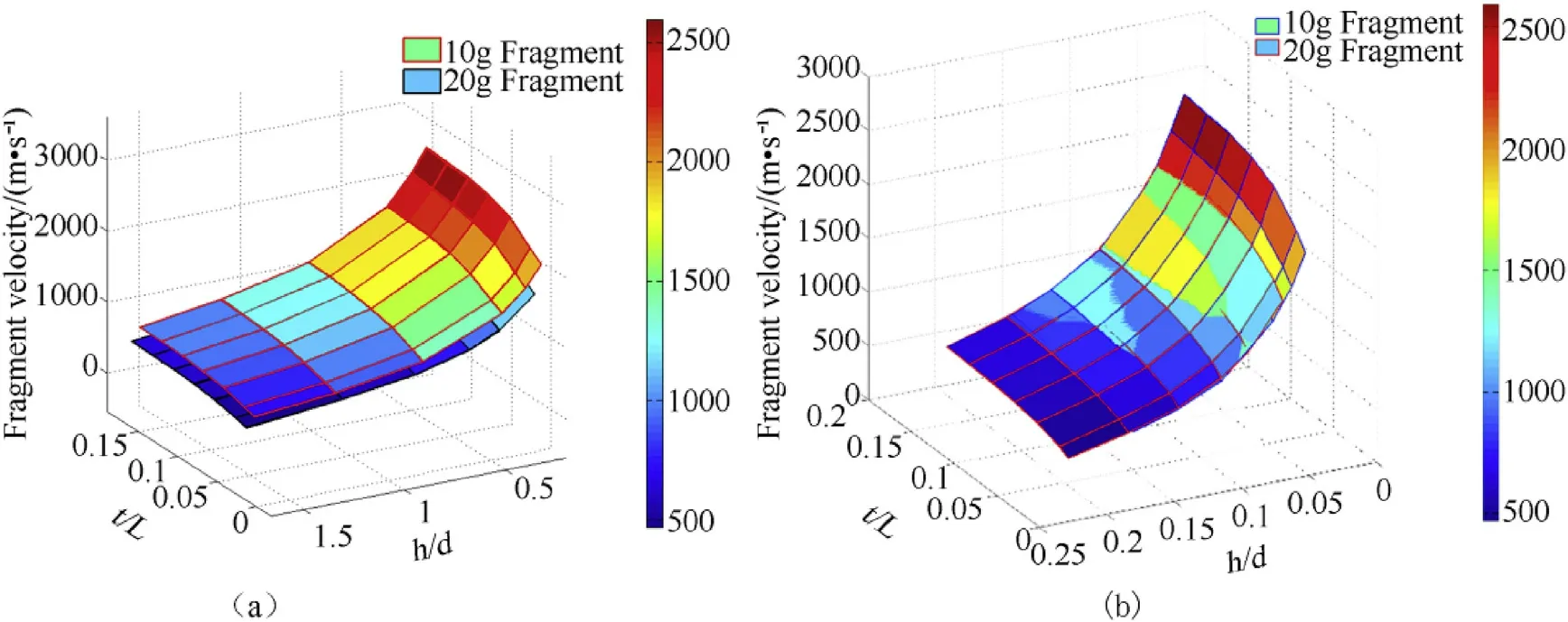
Fig.4.(a)Fragment velocity with t/L and h/d(b)Fragment velocity with t/L and h/L.

Table 7Fragment velocity for different values of t/L,h/L and h/d ratios.
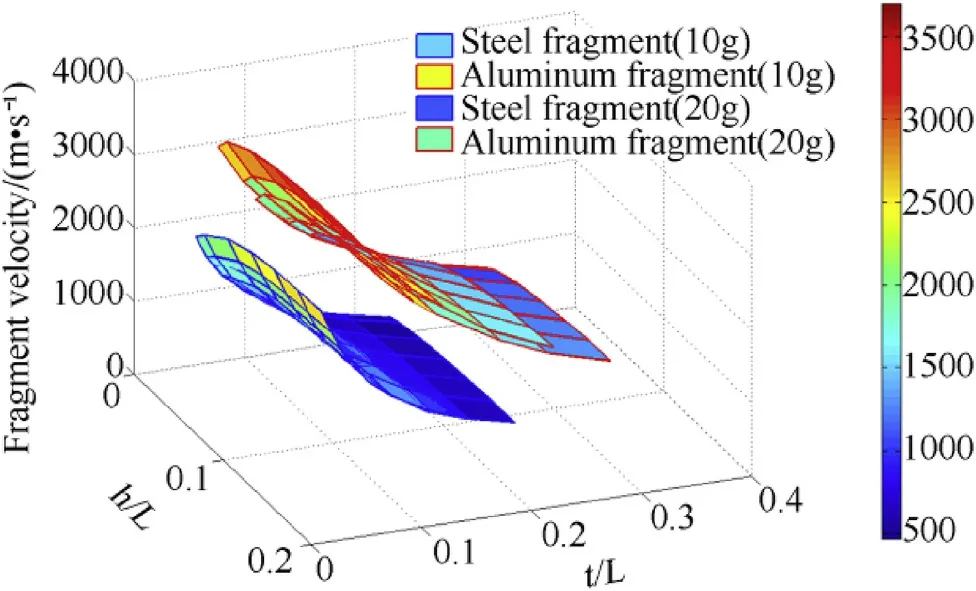
Fig.5.Fragment velocity vs.h/L and t/L for steel and Al fragments.

Fig.6.In f l uence of parameters on fragment velocity(1831 m/s).
Using the above empirical relationship,tw o velocities 1831.92 m/s±35.95 m/s,2523.9 m/s 55.8 m/s required for NATO STANAG 4496 IM test w ere estimated.The variation of fragment velocity(green lines)along w ith 95%con f i dence interval(red lines)as a function of L/D,h/d,Rfand Rcare plotted as show n in Fig.6&Fig.7.It has been observed that,Rfhas the highest slope and slight change in the ratio can affect the fragment velocity signi f i cantly.Therefore,considering the parameters L/D,h/d to be 1.0 and Rcto be 2.0,the expected Rfw as estimated as 3.25 and 5.25 respectively.Once the value of Rfis obtained,the charge length and diameters can be determined based on fragment dimensions and the con f i nement thickness can be w orked out from Rc.
The empirical relation established(Eq.(6))w as further validated w ith experimental data[18].The results are presented in Table 8.Development Establishment,Pune and Vice Chancellor,DIAT,Pune for encouraging to carry out the w ork presented in this article.

Table 8Fragment velocity for 12.1 g and 24.0 g obtained from empirical relationship.
5.Conclusions
1)Increasing the explosive quantity w ill increase the fragment velocity and independent of fragment mass(10 g or 20 g)at any value of Ro.Therefore,overall charge to metal mass ratio(Ro)w hich is dominated by con f i nement thickness and explosive height under con f i nement affects the maximum fragment velocity.
2)The increase in fragment velocity w ith increase in charge L/D ratio increased initially up to 1-1.5 based on charge quantity and thereafter decreased.Hence,L/D should be kept betw een 1-1.5 for such devices.
3)The location of fragment in con f i nement w ill obstruct w hen fragment height is less than the con f i nement height.Therefore,a tapered hole of 45°w ould remove the con f i nement material f l ow ing over the fragment.
4)Increase in front con f i nement increases the fragment velocity and the fragment velocity response becomes asymptotic after certain value of t/L.
5)The h/d ratio and mass affects the fragment velocity.The height of fragment affects Rfcausing reduction in h/d ratio that in turn increases fragment velocity.It was further con f i rmed by changing the fragment material,thus,Rfcontributes signi f icantly to change in fragment velocity.
6)The empirical relationship for charge L/D,fragment h/d,Rfand Rcw ith fragment velocity established can predict the velocity w ithin the reasonable accuracy and w ill help in f i nalization of initial design and dimensions of SCFLED.
Ack now ledgm ents
The authors w ish to thank Director,Armament Research&
杂志排行
Defence Technology的其它文章
- Comparison of burn rate and thermal decomposition of APas oxidizer and PVCand HTPB as fuel binder based composite solid propellants
- Flash X-ray radiography technique to study the high velocity impact of soft projectile on E-glass/epoxy composite material
- Novel colored f l ames via chromaticity of essential colors Ramy Sadek,Mohamed Kassem,Mohamed Abdo,Ahmed Fahd,Hesham Tantaw y,Amir Elsaidy,Sherif Elbasuney*
- Estimation of projected surface area of irregularly shaped fragments Elvedin Kljuno*,Alan Catovic
- Experimental study of bullet-proo f i ng capabilities of Kevlar,of different w eights and number of layers,w ith 9 mm projectiles
- Optimization of gas tungsten arc w elding parameters for the dissimilar welding between AISI 304 and AISI 201 stainless steels
