中国H5N1禽流感病毒传播的动力学研究

高 瑞，张 娟

(1.山西大学 复杂系统研究所， 太原 030006;2.疾病防控的数学技术与大数据分析山西省重点实验室， 太原 030006)

1997年，人感染H5N1禽流感病例首次在中国香港地区出现，之后又有多个国家相继出现[1-2]。据世界卫生组织公布数据知，截止2017年12月，我国实验室确诊感染H5N1禽流感病毒累计病例数为53例，死亡人数为31例，死亡率高达58%[3-5]。据兽医公报公布，截止2017年11月，H5N1高致病性禽流感病毒已蔓延至18个省份[6-7]，感染家禽宿主包括：鸡、鸭、鹅、鹌鹑等，野生宿主包括：江湖海周围的水鸟以及各种迁徙野鸟等[8-10]。由于H5N1高致病性禽流感病毒的传播，已经有近690万家禽被捕杀，给养殖业带来毁灭性的打击[11-12]。现阶段暂无证据表明H5N1高致病性禽流感病毒能在人与人之间进行有效传播，但随着H5N1高致病性禽流感病毒的持续流行与进化，该病毒对人类仍存在严重威胁[13]。

目前，研究禽流感传播与控制的动力学模型大多数以禽个体、人为研究对象，且种间只考虑了禽对人的单向传播。而中国H5N1禽流感病毒的传播特征为：传播速度快，一只家禽携带病毒很快引起整个场群的感染；我国目前以疫点为单位上报政府并进行相应的捕杀；病毒在场群间主要通过养殖业相关人员在场群间的活动进行传播，例如养殖业相关人员的衣着、携带的交通工具等，在禽的调运与销售过程中，将会携带病毒，并在场群之间进行传播与扩散。基于此，本文以场群为单位，以禽养殖与销售场所、养殖业相关人员、普通人群为研究对象，既考虑禽养殖与销售场所对人的感染，又考虑养殖业相关人员携带的病毒对禽养殖与销售场所的感染，建立中国H5N1禽流感场群间传播动力学模型，挖掘其内在传播机制，评估预防控制其流行的有效措施。

1 动力学模型的建立

本文研究对象分为3类：全国禽养殖场与销售场所、普通人群和养殖业相关人员。其中，禽养殖场与销售场所指禽养殖场、活禽交易市场和零售市场；养殖业相关人员指养殖场与销售场所的工作人员，即养殖、运输以及销售活禽的高危人群；普通人群指前往活禽交易市场或者零售市场购买禽的普通民众。根据染病和免疫状态，禽养殖场与销售场所FN分为易感、染病和免疫3种状态，分别记为FS、FI、FV，其中FN=FS+FI+FV；禽养殖场/销售场所中一旦有一只禽染病，该场将认为处于染病状态。根据染病状态，普通人群HN分为易感和染病2种状态，分别记为HS和HI，其中HN=HS+HI；根据衣着、携带工具、交通工具等是否携带病毒，将养殖业相关人员MN分为无携带病毒者、携带病毒者，分别记为MS和MI，其中MN=MS+MI。基于H5N1禽流感病毒的传播特点，该疫病在各仓室之间的转化见流程图1，对应的动力学模型见式(1)。模型中涉及参数的具体意义见表1，其中所有参数都是非负的，且0<α<1， 0<γ<1。

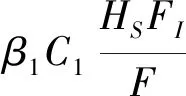
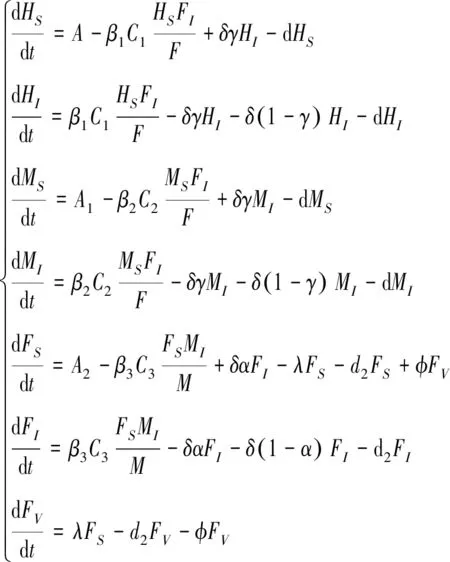
(1)

图1 H5N1禽流感病毒在人和禽养殖场与销售场所之间传播流程

表1 模型(1)中有关参数的说明

观察模型(1)，可得

从而可以得出可行域

Γ={(HS,HI,MS,MI,FS,FI,FV)|HS,

HI,MS,MI,FS,FI,FV≥0,

2 模型的动力学分析

由于模型(1)的后5个方程与前2个方程无关，因此只分析后5个方程即可，组成系统(2)如下：

(2)

2.1 平衡点的存在性

令系统(2)方程右边为0，可以解出模型的平衡点。

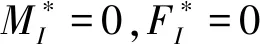
其中：

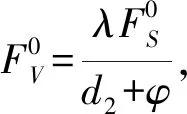
其中,

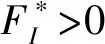
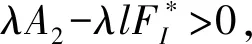
根据上述讨论得出：当R0>1时，系统(2)存在正平衡点E*。

2.2 无病平衡点的局部稳定性

定理1若R0<1，那么系统(2)的无病平衡点E0是局部渐近稳定的。

证明系统(2)在无病平衡点E0处的雅克比矩阵为

可以计算出其特征多项式：

其中，

A=2δ+3d2+d+λ+φ,

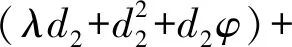
(2δ+d+d2)(λ+φ+2d2)+

很明显，-d是p(λ1)的一个根。

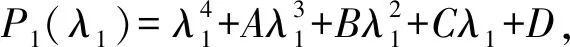
可以得出：

Δ1=A=2δ+3d2+d+λ+φ>0

Δ2=AB-C=(2δ+d+d2) [(2δ+d+d2)×

(2d2+λ+φ)+(δ+d)(δ+d2)×

Δ3=ABC-C2-A2D=

(2d2+λ+φ)(2δ+d+d2)×

(2δ+d+3d2+λ+φ)+(δ+d2)×

(2δ+d)2]}>0

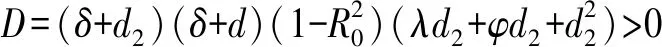
Δ4=DΔ3>0

由Routh-Hurwitz判据，J|E0所有的特征根都具有负实部，因此系统(2)的无病平衡点E0是局部渐近稳定的。

3 防控措施评估

3.1 参数估计

1) 据中国统计年鉴，2004—2017年每年出生人口数的平均值为1 637万[14]，因此A=1.637×107。

2) 从中国畜牧业年鉴可获得2004—2017年全国蛋鸡和肉鸡的总养殖场数[15]。假设每年新增禽养殖场与销售场所为2 000个，根据A2=d2FN，可推算出每年禽养殖场与销售场所的关闭率为6%。

3) 资料显示，H5N1禽流感灭活疫苗的免疫保护期可达半年以上[16]，本文假设为1年，则免疫失效率φ=1。

4) 接种免疫率为接种覆盖率和疫苗有效率的乘积。资料显示，H5N1禽流感灭活疫苗的疫苗有效率为68.4%[17]。本文假设疫苗的接种覆盖率为80%，所以λ=0.55。

5) 据世界卫生组织公布数据知：截至2017年12月，我国实验室确诊感染H5N1禽流感病毒累计病例数为53例，死亡人数为31例，死亡率高达58%[3]，所以1-γ=58%。

6)δ代表恢复率，一年内感染者百分之百移出，要么恢复，要么死亡，因此取δ=1。

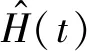
HS(0)=1.3×109×0.7,HI(0)=2

MS(0)=1.3×109×0.3,MI(0)=1

FS(0)=1.114 927 6×108×0.7

FI(0)=50

FV(0)=1.114 927 6×108×0.3

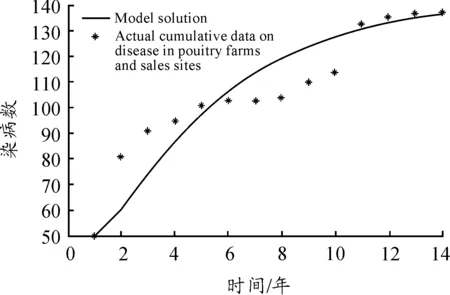
图2 2004—2017年禽养殖场与销售场所染病数据

3.2 敏感性分析

利用表1的数据和基本再生数的表达式，可以估计出中国H5N1高致病禽流感在场群间传播的基本再生数R0=0.832 4。说明在目前的免疫与扑杀作用下，该疫病随着时间推移将会得到控制。在实际中，H5N1抗原在持续的免疫压力下不断进化，发生基因变异，使得疫苗对其保护效果越来越差，即接种免疫率λ会降低，因此偶尔仍会有疫病暴发。现在讨论疫苗免疫率对疫病流行的影响。为了评估免疫等措施对疫病流行的影响，讨论R0关于各参数的敏感性。由图3可知：当其他参数值不变时，随着λ降低，基本再生数R0将会增大。当λ小于0.1时，R0将大于1。

接下来实施双参数分析，来讨论C2、C3、d2和λ对R0的作用。由图4知：随着C2和C3的减小，基本再生数R0将会降低。随着d2和λ的增大，也会使基本再生数R0不断地降低。由图4(a)～(d)知：如果按照当前每年养殖场的关闭率d2=0.06，接种免疫率λ=0.55,C2需小于1 010,C3需小于40 384,才能保证R0<1。由图4(e)知：曲线斜率比较大，说明R0对β3较敏感，即控制染病养殖业相关人员对场群的传染力是非常重要的。通过以上分析得到：监控养殖业相关人员对场群的感染，加强养殖业相关人员及其携带工具的消毒，增加养殖场接种免疫率，可有效控制传染力度。

图3 λ对R0的作用

图4 双参数敏感性分析C2、C3 、d2、λ 、β2和β3对R0的作用

4 讨论

基于H5N1禽流感病毒的传播特征，本文以场群为单位，以禽养殖场与销售场所、养殖业相关人员、普通人群为研究对象，既考虑禽养殖场与销售场所和养殖业相关人员之间的双向作用，建立中国H5N1禽流感场群间传播动力学模型，挖掘其内在传播机制，估计了中国H5N1禽流感传播的基本再生数R0，评估预防控制其流行的有效措施。通过分析得到，在免疫与扑杀禽的作用下，中国H5N1禽流感传播能暂时得到控制，然而，由于病毒变异重组，接种免疫率λ会降低，会导致基本再生数R0大于1，使得疫病再次暴发。进一步分析得到，监控养殖业相关人员对场群的感染，加强养殖业相关人员及其携带工具的消毒，增加养殖场接种免疫率，可有效控制H5N1禽流感病毒的传播。在未来的工作中，将研究病毒变异与疫苗替换对疫病流行的影响。