大数据环境下利用新型FTS的并行细节点指纹匹配通用分解方法

李庆年，胡玉平

(1.南宁学院 信息工程学院， 南宁 530200; 2.广东财经大学 信息学院， 广州 510320)

指纹识别是近二十年来的研究热点[1]，随着硬件技术的快速发展，使用识别技术的机构和公司与日俱增。指纹呈现出多种特征，根据这些特征可以更好地实现精准识别。在这些特征中，细节点是应用最广泛的特征之一。识别算法通常从指纹细节点中提取一组结构进行计算[2]，在模板指纹数据库中寻找给定的输入指纹。验证旨在评估2幅图像是否对应同一指纹。与许多其他图像匹配出现的问题一样，由于空间中存在图像变形、信息缺失等因素，因而验证具有很高的复杂性[3]。此外，由于涉及特征之间的多种比较，识别技术实质上比验证更加复杂。为了克服识别中存在的困难，学者们提出了分类和索引等技术[4-5]。

当数据库中的数据量较大时，指纹识别问题的复杂性变得更高，尤其是识别时间，其与匹配数呈线性增长关系[6]。庞大的指纹数据库对指纹识别构成了挑战。在过去几年，科研人员提出了几种使用大规模高性能计算体系结构来处理大数据问题的框架，这些框架中最流行的是Apache Hadoop[7]和Apache Spark[8]。Apache Hadoop是MapReduce范例的一种开放源码，它将数据构造成一组key和value的组合对，将这些组合对分为2个阶段进行处理：Map阶段和reduce阶段。在Map阶段，每个映射操作接收一个单线对，并输出一组它所产生的线对。将所有映射阶段的中间线对进行洗牌和排序，以便每个reduce操作都接收相同key。reduce操作的结果也可表示为一组关键value对，这些关键value对存储在HDFS中。Apache Spark同样将HDFS用作底层文件系统，但会将数据分组为弹性分布式数据集(RDD)。Spark将这些RDD尽可能多地保存在内存中，以减少I/O磁盘容量。Spark提供了一组转换(将一种RDD转换为另一种RDD)和操作(将RDD转换为某种结果)，这些转换和操作可以随意组合，以创建不同的工作流程。负载平衡战略[9]、虹膜识别的并行化[10]等方案都是利用这些框架来解决生物特征识别的问题。

基于上述分析，本文在大数据框架中处理并行指纹识别问题时，提出了一种基于新型指纹拓扑结构(fingerprint topology structure,FTS)的指纹匹配分解方法。主要创新点如下：

1) 提出了一种基于细节点的置信度指纹匹配算法，有助于全局范围的指纹信息提取，从而确保局部相似细节点的有效匹配。

2) 提出的分解方法在指纹匹配过程中考虑了更好的并行性，允许丢弃局部结构中检测到的非匹配的子集，从而可有效使用和输入局部结构的模板信息，增加了识别输入指纹的灵活性。

3) 将提出的分解方法在Apache Hadoop和Apache Spark框架上实现，通过与现有的MPI系统上的实验结果进行比较，验证了该方法的可靠性。将分解方法应用于2种不同的匹配算法(Jiang算法[11]和细节点圆柱代码(MCC算法)[12])中，通过实验验证了所提出分解方法的通用性。

1 基于细节点特征的指纹匹配

1) 全局匹配方法。寻找2个细节点集的最佳对准，使用指纹的全部信息实现匹配，该方法虽然提供了较高的清晰度，但是对指纹采集的失真较为敏感。

2) 局部匹配方法。从细节点集中提取局部结构，并对这些局部结构进行比较，以确定它们的相似性。该方法通常不受平移和旋转的影响，因此对失真不太敏感。

(1)

识别问题即在包含n个指纹T={T1,…,Tn}的模板数据库中查找输入指纹Ij。大多数识别系统通过将Ij与每个模板指纹Ti进行比较来完成n个验证，并返回产生最大分数的标识：

(2)

这种识别系统的识别时间关于n呈线性增加。因此，当n很大时，识别时间往往过长。

2 提出的指纹匹配通用分解方法

本文提出了一种适用于基于细节点的指纹匹配算法的通用分解方法。它将匹配过程分解为较小的步骤，这些步骤以并行和灵活的方式计算，从而及早发现不匹配指纹并加快处理速度。

2.1 新型指纹拓扑结构

在传统的指纹拓扑结构中，通常只提取某一种特征。文献[15]利用提取出的纹线特征，通过对比纹线达到指纹匹配的目的。文献[16]利用中心点附近的方向场实现指纹匹配，该算法提取的是邻域特征。本文中把细节点特征、脊线特征以及邻域特征三者结合起来，实现了一种新型指纹拓扑结构。

在指纹的特征识别中，叉点包含的信息量更大，且不易受到外部条件的干扰。基于此，本文将脊线跟踪应用到叉点的3个分支中，如图1所示。o点表示叉点，a、b、c点表示脊线点，顺着3个分支可到达a、b、c三点。令叉点和3个脊线点的方向角差分别为α、β、γ，叉点和3个脊线点间的长度分别为oa、ob、oc，并将它们存入到特征向量中。用(x,y)表示叉点的坐标，在特征点的类型中，用E表示端点，用F表示叉点，则叉点的特征向量可以表示为{(x,y),F,(α,oa),(β,ob),(γ,oc)}。

图1 叉点拓扑结构

由于端点仅存在于一条脊线上，它所包含的脊线特征以及邻域特征较少，所以使用k近邻算法来提取端点附近的有用特征。在图2中，根据k近邻算法寻找离叉点o距离短、并且处在环形区域中的3个脊线点，这3个脊线点就可以作为邻域特征点。接着，利用脊线追踪的方式寻找到最终的脊线点a、b、c。整个过程中，组成环形区域的2个圆的半径分别为R1和R2，端点和3个脊线点的方向角差分别为α、β、γ，端点和3个脊线点间的长度分别为oa、ob、oc，并将它们存入到特征向量中。用(x,y)表示端点的坐标。在特征点的类型中，用E表示端点，用F表示叉点，则端点的特征向量可以表示为{(x,y),E,(α,oa),(β,ob),(γ,oc)}。

图2 端点拓扑结构

2.2 提出的基于置信度的匹配算法

假设p和p′分别是2个细节点的不同集合，且它们各包含Np和Np′个细节点，则可以得到Np和Np′个细节点的拓扑结构以及1个相似度矩阵SLS，该矩阵的元素个数为Np×Np′。令M={ii′}为p和p′之间的最优匹配，则该最优匹配可表示为一个寻找最优的问题：

(3)

用以下二值优化问题的解代替该问题的解：

m0=arg max(msT),m∈{ 0,1}NpNp′

s.t. |1pm*|≤|1p| and |m*1p′|≤|1p′|

(4)

式中：M表示匹配关系；m表示M相对应的1×NpNp′的行向量；s表示SLS相对应的1×NpNp′的行向量；m0表示最优解，它是一个二值向量。m可以表示成一个矩阵形式m*，m*的大小为Np×Np′，m*(i,i,)=1即表示细节点i和i′相互匹配，而m*(i,i,)=0则表示这2个细节点不匹配；向量1p表示一个值全为1的、大小为1×Np的行向量，向量1p′则表示一个值全为1的，大小为1×Np的列向量。在约束条件中，p和p′集合中的细节点互相匹配，|1p|表示1p的l1范数。

在传统的指纹识别方法中，细节点的局部相似度能在局部区域内衡量相似程度，而在全局范围上，局部相似的细节点很有可能不能相互匹配。因此，本文提出了置信度的概念，它描述了一组细节点对在该全局范围内与候选点之间的匹配可能性。对于p和p′两个细节点的集合来说，置信度矩阵CGC包含Np×Np′个元素，关联矩阵用TM来表示，其中TM(i,i′)=CGC(i,i′)×SSL(i,i′)，则匹配问题可以转化为

(5)

可以使用下列二值优化问题的解代替该问题的解：

(6)

其中：t表示与矩阵TM相对应的行向量，其大小为1×NpNp′；M表示匹配关系；m表示M相对应的1×NpNp′的行向量；m0表示最优解，它是一个二值向量。指示向量m可以表示成一个矩阵形式m*，m*的大小为Np×Np′。m*(i,i,)=1表示细节点i和i′相互匹配，而m*(i,i,)=0则表示这2个细节点不匹配。向量1p表示一个值全为1的、大小为1×Np的行向量，向量1p′表示一个值全为1的、大小为1×Np的列向量。在约束条件中，p和p′集合中的细节点互相匹配，|1p|表示1p的l1范数。

2.3 匹分解法

(7)

基于部分分数的概念，定义了2个聚合这些分数的函数，用来以并行且灵活的方式计算最终匹配分数qij。

1) 函数Qp将1组kp部分分数与单个新的部分分数聚合，如方程式(8)所示。需要注意的是，kp为正在聚合的部分分数的数量，它与2个指纹中任何一个局部结构的数量均无关。因此，函数Qp的输出是由2个指纹中得到的局部结构的kp子集中计算出来的部分分数。

(8)

2) 在单局部分数上应用方程式(9)中定义的函数Qf，单局部分数包含所有Ti和Ij局部结构之间的相似性聚合信息，并计算出最终匹配分数qij。

(9)

当保持函数Qf固定时，这2个函数允许以非常灵活的方式聚合部分分数，从而使匹配算法具有细粒度并行化以形成最终匹配分数。

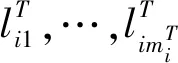
3 匹配方法的并行化

3.1 将匹配方法嵌入到MapReduce

上文定义的分解法可以表示为MapReduce范式中的问题。假设模板数据库由所有nT模板指纹的局部结构组成。本文提取将要识别的nI输入指纹的局部结构(通常nI≪nT)，假设在MapReduce匹配过程启动之前，先将这些本地结构存储在分布式文件系统中。

映射 (k1,v1)→ 列表 ({k2,v2},∀j∈{1,…,ni})

(10)

映射为每个输入生成nI个输出记录，因此将2个指纹的标识符作为key，将所产生的部分分数发送到reduce函数。每个reduce函数合并给定的模板对以及输入指纹以生成最终匹配分数，如方程(11)所示。将这些分数写入分布式文件系统。

(11)

此外，在中间组合阶段聚合部分分数集，从而最小化mapper和reducer之间的网络和磁盘流量。在MapReduce中，组合器可以在记录上应用多次或一次不用，这意味着它必须是可结合的、可交换的。基于集合的定义，提出的分解自然地符合这些要求：

(12)

图3(a)给出了本文方法在MapReduce中的流程。图3(b) 给出了每个映射的工作流程，其中局部匹配在映射中执行。

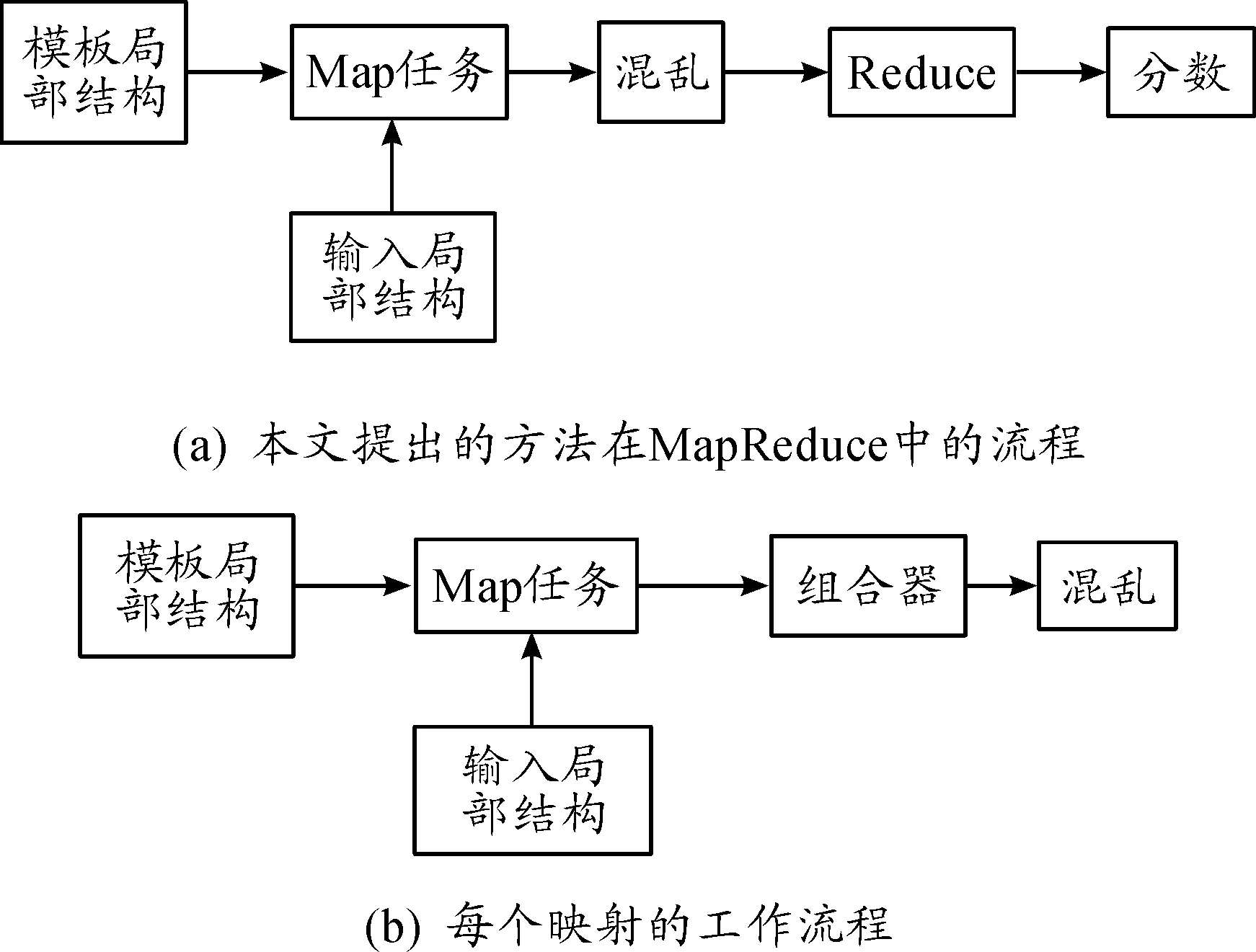
图3 MapReduce框架中执行过程的流程

3.2 将匹配方法嵌入到Spark

提出的分解方法不仅适用于MapReduce，还可用于Apache Spark中设计高效识别框架，如算法1所述。

算法1 对Spark分解的适应性的伪代码输入RDD广播输入的RDD模板RDD模板RDD.GroupByKey()当lTIK∈TemplateRDD时,执行 当lTj∈InputRDD时,执行 ps=p({lTik},LIj) psRDD.insert({i, j},ps) 结束结束FinalpsRDD=psRDD.reduceByKey(Qp)ScoresRDD=FinalpsRDD.mapValues(Qf)

4 2种经典的匹配算法

4.1 细节点圆柱码匹配算法

细节点圆柱码(minutia cylinder-code，MCC)[12]匹配算法使用有圆柱状支撑的局部结构。圆柱体包含关于细节邻域的信息，将圆柱体编码成一个大小为NsNsNd的实数向量。局部匹配由计算每对圆柱(1个Ti和1个Ij)之间的相似性组成，从而获得矩阵Γ，其中γ是相似函数：

(13)

Cappelli等提出了4种计算全局分数的合并技术，本文主要研究局部松弛相似度排序(LSSR)。

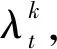
(14)

(15)

通过平均具有np个最高效率的松弛相似性计算全局分数。

4.2 Jiang匹配算法

Jiang匹配算法[11]使用基于每个细节点的Nn个最近领域的局部结构，每个局部结构均可描述为实数向量，所有局部结构对之间的相似性矩阵都遵循方程(13)的形式。全局匹配包括对局部结构的最佳匹配对进行整理，并根据这种配对对齐所有其他细节点。从每一个细节点中得到一个旋转平移不变向量Fgk。然后，对每一对对齐的细节点计算匹配确定性级别ml(r,s)：

(16)

最终匹配分数计算如下：

(17)

5 实验和分析

通过实验验证提出的匹配算法和分解方法性能，并将Jiang匹配算法、MCC匹配算法应用于提出的分解框架中进行实验。实验中，提出的基于置信度的匹配算法分别在Apache Hadoop和Apache Spark中实现，Jiang匹配算法、MCC匹配算法在MPI中的实现结果均参考文献[16]的实验结果。

5.1 测试结果

通过SFinGe软件[17]生成了具有400 000个模板指纹的数据库。通过采用模板指纹的5 000个附加印模，以及数据库中不匹配的额外5 000个指纹，建立了10 000个输入指纹集。图4为部分指纹图像示例。SFinGe数据库的统计数据如表2所示。

图4 SFinGe数据库部分指纹图像示例

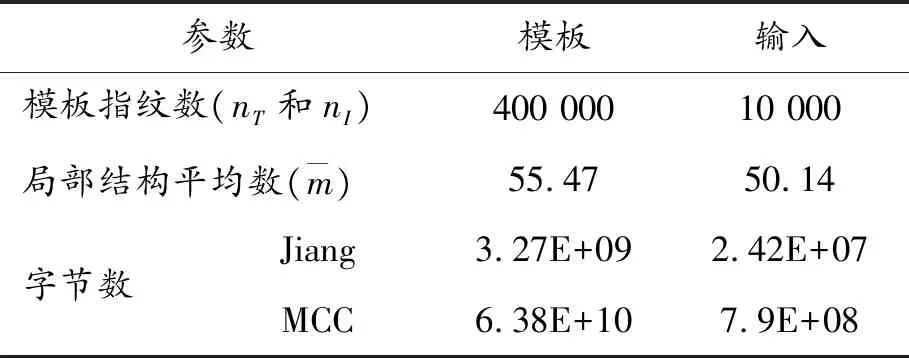
参数模板输入模板指纹数(nT和nI)400 00010 000局部结构平均数(m)55.4750.14字节数Jiang3.27E+092.42E+07MCC6.38E+107.9E+08

尽管在3种比较框架(MPI、Hadoop和Spark)中使用了相同的算法，但由于浮点运算误差，所得结果的精度各不同。对于3种比较框架，表3给出了获得SFinGe数据库的TPR(真阳性率)。从表3可以看出，3种框架下的值非常相似，只有略微的差异。Jiang匹配算法和MCC匹配算法在MPI框架下的实验数据参考文献[16]的实验结果，通过对比可以看出，提出的分解框架具有良好的可靠性。

表4所示为3种框架下3种匹配算法的平均识别时间。从表4可以看出，相比其他2种匹配算法，本文的基于置信度的匹配算法在这几种框架中的识别时间方面有很大的优势。总体而言，几种匹配算法嵌入提出的分解框架后，均获得了较好的识别性能。提出的分解方法能以灵活的方式识别输入指纹，从而有效地使用输入局部结构的模板信息。安全丢弃部分分数增强了匹配过程的可靠性，由于允许对非匹配指纹或非相似指纹部件进行早期检测，从而减少了计算量。

表3 获得SFinGe数据库的TPR(FPR为0%)

表4 SFinGe数据库上的平均识别时间 s

表5所示为3种匹配算法嵌入提出的分解框架后在Hadoop中实施时的统计数据。从表5可以看出，组合阶段得到了较好的优化，这是因为传递给reducer的部分分数非常低，从而导致在洗牌阶段需要较少的网络流量。大部分计算时间用在映射阶段，该阶段计算所有局部相似点。

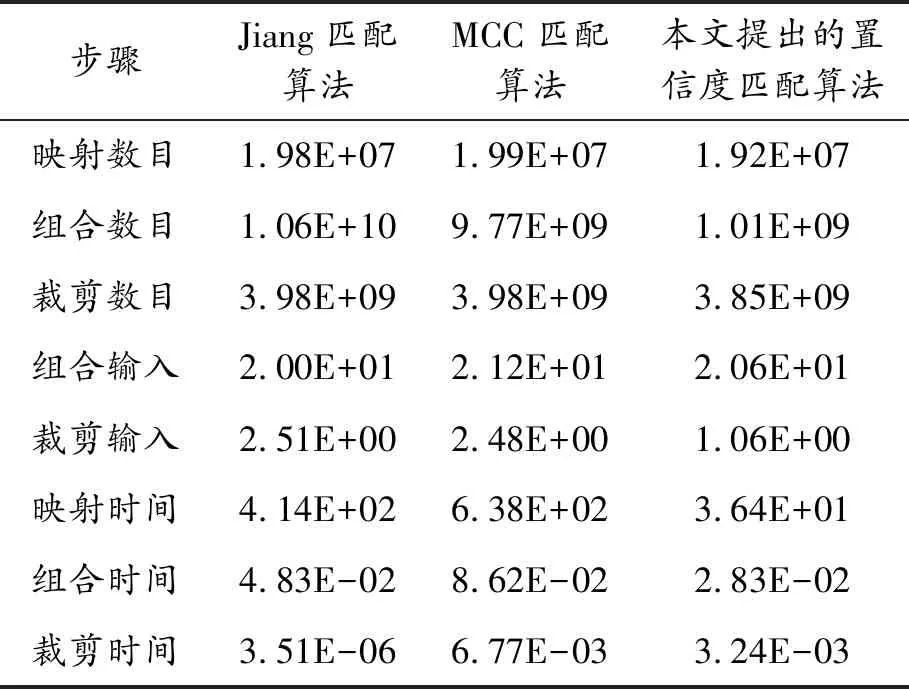
表5 使用Hadoop执行的统计数据

表6所示为Spark中每步的平均时间。需要注意的是，各阶段是同时执行的，因此总的时间远低于各个阶段的时间总和。首先，在整个计算节点上实施数据库加载，这样就可以在考虑加载数据大小的情况下，从分布式文件系统中快速完成加载。对于每个指纹，输入指纹的传播要花费更多的时间。计算匹配结果和将结果写入HDFS消耗了大量时间，且它们所消耗的时间基本相同。

表6 Spark中每步的平均时间 s

综合表3～6的测试结果显示，3种匹配算法的识别性能均良好，各个步骤的统计数据和所用时间均在可接受范围内。由此可见，提出的分解方法具有良好的可靠性。

5.2 提出的分解框架的通用性分析

本文中所提出分解方法的关键是考虑可扩展识别系统，使用SFinGe数据库中多个尺度的子集，利用Hadoop和Spark评估可扩展性。在每种情况下，将输入指纹的数目设置为模板数的10%，其中一半是冒充身份，最大数量可达10 000。因此，最大的数据库计算为4×109个匹配。

图5所示为Hadoop、Spark框架下3种匹配算法的吞吐量与模板指纹数量之间的关系。从图5可以看出，虽然Spark的吞吐量高于Hadoop，但当模板数量增加时，这2个框架呈现出了相同的特性：对于大型数据库，随着计算时间与通信时间呈比例增加，吞吐量也不断增加。通过分析在大数据框架中的测试结果可知，提出的分解框架可以较好地适用于3种不同的匹配算法，提出的分解方法具有良好的通用性。

图5 2种大数据框架下3种匹配算法的吞吐量

6 结束语

本文中提出了一种面向细节点指纹匹配的通用分解方法，并将其在Apache Hadoop和Apache Spark 2种大数据计算框架中进行实现，验证了该方法的可靠性。将所提出分解方法应用于3种匹配算法进行实验，验证了分解方法的通用性。综合可知，先提取出细节点特征，然后将匹配分数的计算分解为较低级别的步骤有助于提高匹配过程的灵活性。

在下一步研究中，考虑将提出的分解框架部署于其他的大数据或并行计算环境实现，例如MPI。此外，还可将分解方法应用于其他的指纹匹配算法，进一步提升该方法的可靠性和通用性。