基于汉明距离与免疫思想的粒子群算法
2019-05-23丛培强陈亚茹
丛培强,李 梁,陈亚茹
(重庆理工大学 计算机科学与工程学院, 重庆 400054)
粒子群算法(particle swarm optimization,PSO)是Kennedy Eberhart受鸟群觅食启发提出的一种并行群体智能算法[1]。该算法是基于种群的搜索算法,模拟鸟群的社会行为,可以解决多峰值、多目标、非线性问题,已广泛应用于函数优化、模糊控制等多个领域[2-5]。粒子群算法原理简单,易于实现,但也存在诸多缺点,如易陷入局部最优解、后期收敛速度慢、易早熟等。针对上述缺点,许多学者提出改进措施。文献[6]中提出一种自适应小生镜粒子群优化算法,虽然解决了粒子群早收敛的缺点,但是存在易陷入局部最优解问题。文献[7]中提出了不需要参数的小生境粒子群算法,克服了标准粒子群算法在搜索后期易陷入局部最优解等缺点。文献[8]中提出粒子群动能的概念,解决了参数选择的问题。文献[9]中提出一种新的种群生成策略,通过遍历种群中个体来选取适应值最优的数值作为种子,然后将粒子群分为若干个相互独立的种群。文献[10]中提出改变粒子群惯性权重的定义方式,采用随机权重和异步变化策略,提高了搜索速度和精度。以上方案虽然解决了粒子群算法的易早熟、后期收敛速度慢等问题,但是由于无法表示粒子位置与速度参数,不适合求解离散问题。针对以上问题,本文提出一种基于汉明距离与免疫思想的改进粒子群算法(IHPSO),通过引入汉明距离、免疫疫苗以及免疫选择等免疫思想来提高收敛精度。
1 粒子群算法
1.1 标准粒子群算法
粒子群算法(PSO)是一种基于群体的全局优化算法。在粒子群算法中,每个粒子代表原始问题的一种可行解,群体中每个粒子都有相应的位置与速度。粒子群算法步骤如下:
步骤1初始化粒子群参数。设种群规模为m,即定义m个粒子,为每个粒子初始化相应位置zid(t)={zi1,zi2,…,zim}和速度vid(t)={vi1,vi2,…,vin},并计算适应度。其中zid(t)和vid(t)分别表示第t代第i个粒子的位置和速度。
步骤2在解空间中粒子持续更新位置与速度信息搜索新的解。每一次迭代中的粒子更新条件是历代中该粒子本身搜索到的最优位置pid和整个粒子群历代搜索到的最优位置pgd。
步骤3计算vid(t+1)和zid(t+1)的速度更新公式。
vid(t+1)=wvid(t)+η1rand()[pid-zid(t)]+
η2rand()[pgd-zid(t)]
zid(t+1)=zid(t)+vid(t+1)
其中:vid(t+1)表示第t+1代中第i个粒子在第d维的速度;w表示惯性权重;η1、η2为加速系数;rand()为[0,1]范围的随机数。
步骤4寻找到最优解或达到最大迭代次数时,算法结束。
1.2 汉明距离
汉明距离是一种距离的度量方式。若存在2个等长字符串,其相应位置上不同字符的个数即汉明距离。例如,2个二进制字符串a=[1,3,5,7,9]与b=[2,3,5,6,9],则a与b间的汉明距离为3。汉明距离已实际应用。解决了众多问题,如Rai等[10]将支持向量机和汉明距离相结合运用于虹膜识别系统,得到较高的识别率;Osaba等[11]引入汉明距离的概念,利用蝙蝠算法求解 TSP 时改进了该算法中对蝙蝠速度的定义。
在TSP问题中,用1维数组表示每个可行解,不同解数组之间长度相同,数组内序号排列顺序不同。如存在8个城市的TSP问题,设t时刻有2个可行解数组:xt1=[2,6,4,3,1,5,7,8],xt2=[1,6,4,7,3,5,2,8],则xt1与xt2之间的汉明距离为4,记为HMD (xt1,xt2)=4。用这种城市序列表示解的方式会存在循环闭合回路,不同解序列可能会表示同一个解。如路径[2,4,3,6,1,7,8,5],[8,5,2,4,3,6,1,7],这2个解序列长度相同,虽然解中城市序列不同,但是当2个解数组归一到同一城市起点时,容易发现这2个解序列代表同一城市路径。因此,运用汉明距离概念求解TSP问题时,需要对每个粒子的解进行预处理,即调整每个解的城市序列,将所有解序列的起始城市节点归一为相同节点后再计算汉明距离。

2 免疫思想
2.1 算法思想
人工免疫算法(AIA)模拟生物免疫系统中免疫进化机理进行抗原识别和抗体繁殖过程,促进高亲和度抗体,抑制高浓度抗体,保持抗体多样性,是一种计算最优解的智能优化算法[12]。抗原代表原始问题,即目标函数和约束条件,抗体代表原始问题的可行解。
抗体的亲和度表示抗体与抗原间的匹配程度,即该抗体表示的可行解接近最优解的程度。亲和度越大则抗体越有可能是最优解。抗体的浓度表示抗体间的相似程度,浓度越大则抗体间表示的可行解越相似。遗传的下一代应尽量保持高亲和度、低浓度。保持高亲和度能使求得的可行解尽快地接近最优解,提高收敛速度。低浓度能增加解的分散性,提高解的多样性,防止陷入局部最优解,提高算法全局搜索能力。另外,粒子群算法引入生物免疫系统的免疫记忆细胞、免疫疫苗、免疫选择等机理。记忆细胞为亲和度较大的抗体组成的抗体群,免疫疫苗为抗体中优秀的基因。在TSP问题中,免疫疫苗为最优路径中相邻的几个城市节点。
2.2 相关定义
2.2.1亲和度
亲和度表示抗体与抗原的相似程度,亲和度越大表示当前粒子越接近最优解。亲和度记为affinity,计算公式如下:
(1)

2.2.2浓度
浓度表示抗体间的相似程度,间接表示种群的多样性,浓度越大则种群多样性越小。本文采用区间法表示抗体的浓度。设存在n个抗体,每个抗体的亲和度为affinity1、affinity2、…、affinityn,将这些值按由大到小顺序排列,等分为k个区间[affinity1,affinityi]、[affinityi+1,affinityj]、…、[affinitym,affinityn],记为L1、L2、L3、…、Lk。统计每个区间的适应度之和sum(m),m表示第m个区间,则第m个区间内的抗体浓度为sum(m)/k。定义某个区间的浓度为D(Lk),每个抗体的浓度定义为individuali。由此,每个区间内的抗体浓度均相同,促使某些浓度太小但有很大潜力的抗体可以遗传到下一代,从而保证群体多样性。
2.2.3选择概率
抗体在进化过程中,希望亲和度高但密度小的抗体被促进,亲和度小但密度大的抗体被抑制,因此,基于联合亲和度和密度的概率构建如下:
(2)
(3)
联合亲和度与浓度的统一选择概率P为:
Pi=∂Pa(i)+(1-∂)Pb(i), ∂>0
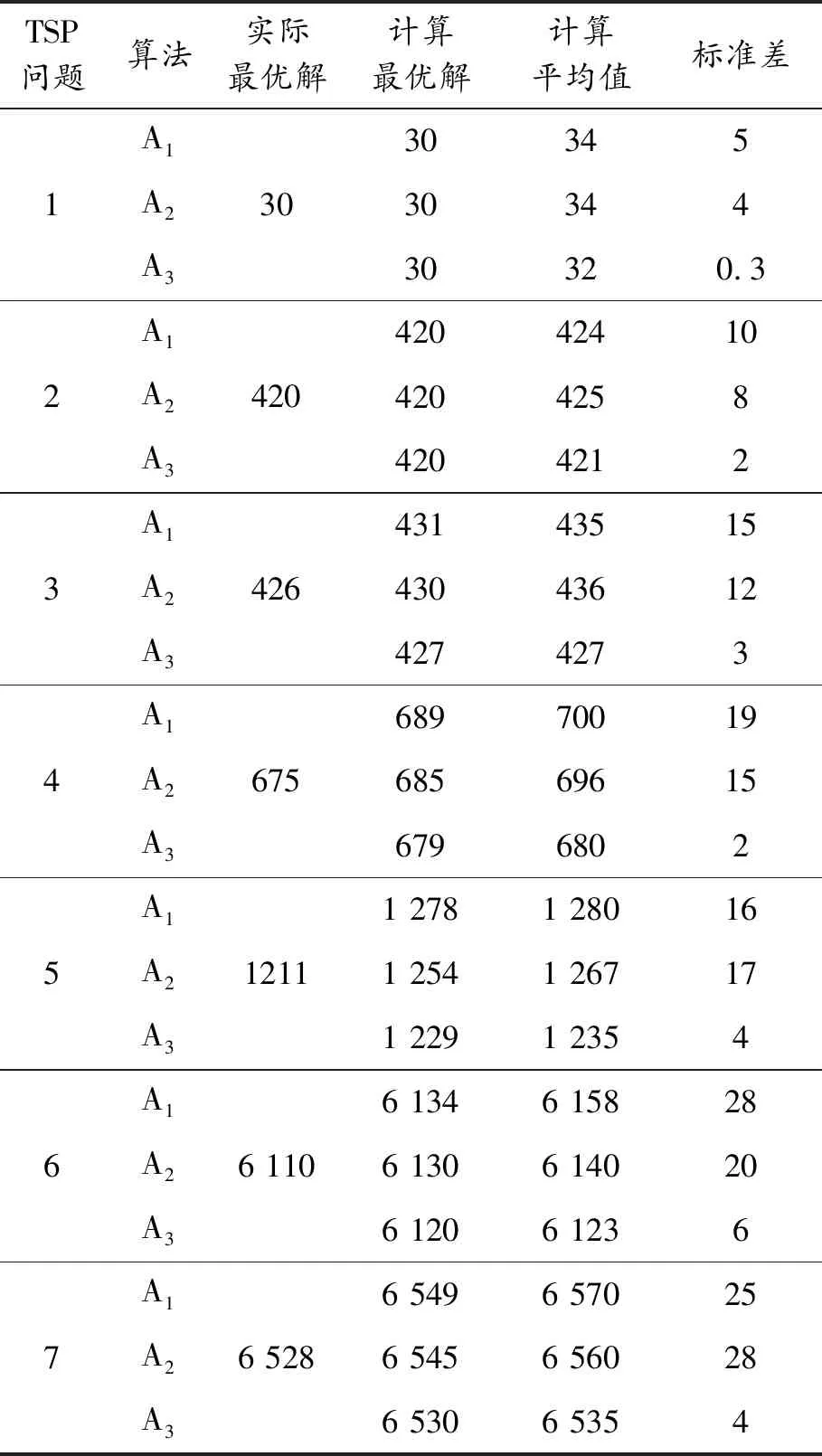
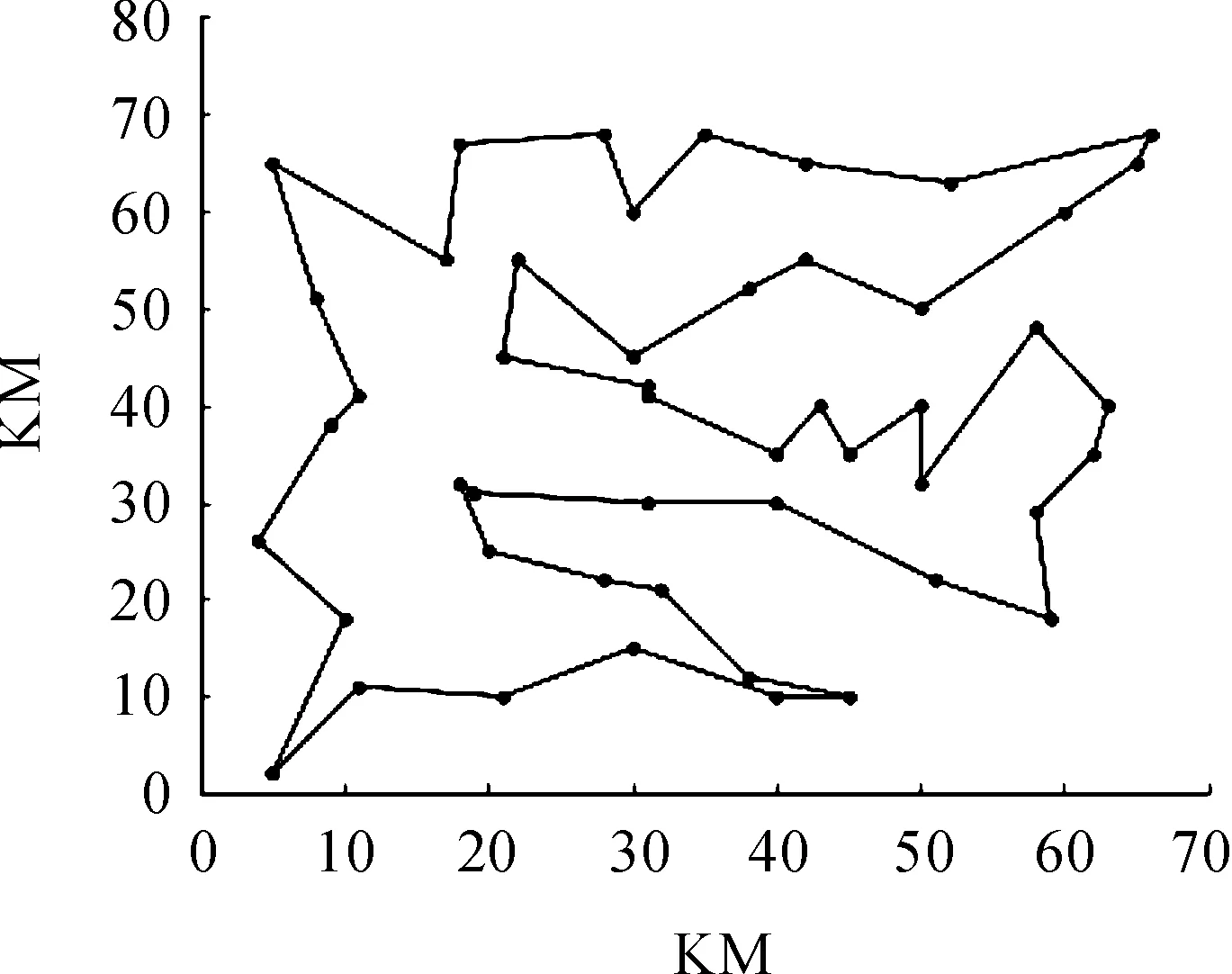
0 (4) 由式(4)可知:选择概率统一考虑亲和度与密度,由∂调节亲和度与密度对最终抗体选择概率的影响程度。∂越大,则抗体亲和度对抗体选择概率的影响程度越大,反之,则密度对抗体选择概率的影响程度越大。 2.2.4免疫疫苗 免疫疫苗指抗体中一段优秀的基因,很大程度上会存在于最优解中的部分解中。免疫疫苗如果能代代遗传则能大大提高粒子群的收敛速度。对于TSP问题,多条最短距离中很大程度会包含相同的相邻城市节点,这是TSP问题本身具有的特征[13],这些相同的相邻城市节点即免疫疫苗。若存在2个最优抗体都对应最优解,则免疫疫苗的求解方式是求2个最优抗体的交集。邹鹏等[14]证明了全局最优解包含局部最优解的80%。因此,本文引入免疫疫苗能加快算法的收敛速度。 2.2.5免疫疫苗接种 免疫疫苗接种即按照一定比例选取适应度小的n个抗体,使用免疫疫苗对其进行更新操作。以TSP问题为例,更新过程如下: 若存在免疫疫苗V及需要接种的抗体A,疫苗长度为|V|,抗体A长度为|A|,s为V的第1个城市,e为V的最后1个城市。 i=1 j=i+|V|-1 while (i<|A|-|V|+1) { if (A(i)==s&&A(j)==e) { 将A(i)~A(j)的城市节点替换为免疫疫苗中的城市节点,A(i)~A(j)外的城市节点做相应变换,保持原城市节点总数不变。 } } 基于汉明距离与免疫思想的粒子群算法(IHPSO)在更新速度与距离时引入汉明距离的概念,并引入免疫疫苗、抗体选择等概念,加快了粒子的收敛速度,提高了收敛精度。算法流程如图1所示。 步骤1初始化城市间距矩阵。即在2维空间中设置每个城市坐标,计算城市间距离。 图1 算法流程 步骤2初始化粒子群相关参数,即初始化粒子的速度与位置。 步骤3根据式(1)计算每个抗体的亲和度,并在此基础上计算局部最优解pbest与全局最优解Gbest。 步骤4判断是否满足迭代终止条件,如果满足则输出结果;否则继续执行。 步骤5生成免疫记忆细胞。即筛选所有抗体,选择亲和度较大的n个抗体组成先进抗体群作为免疫细胞,根据具体问题人为确定免疫细胞包括抗体的数量。 步骤6生成免疫疫苗。免疫疫苗为问题本身具有的天然特征,任选2个最优抗体进行相交操作,将交集单独存储作为免疫疫苗。 步骤7计算每个粒子与最优粒子的汉明距离,并更新粒子的速度与位置。这种更新速度与位置的方法不同于传统粒子群算法或改进算法,该方法不涉及惯性权重、随机因子等,避免了调参过程。 步骤8步骤7对粒子进行更新操作,产生m个新的抗体,再从免疫细胞中选取q个抗体组成新的抗体群。 步骤9根据式(4)计算每个抗体的选择概率,根据选择概率大小选出x个抗体组成接种抗体群,x由人为指定。 步骤10免疫疫苗接种。按照一定比例,对亲和度较低的抗体进行疫苗接种。计算接种后的抗体适应度,若该适应度小于接种前抗体的适应度值,则不对该抗体进行接种操作。 步骤11转至步骤4,继续执行。 选取TSPLIB测试库中一些数据实例作为测试数据集,在处理器为Intel Core i5-5200U 2.2 GHz、内存为8G的计算机上使用Matlab进行仿真实验,验证本算法的可行性。 采用基于汉明粒子群算法(HPSO)、基于汉明距离与免疫思想的粒子群算法(IHPSO)以及文献[15]中自适应离散粒子群算法(SADPSO),在测试集上进行200次迭代实验,对比实验结果验证本算法的性能。基于上述3种方法在以下数据集上进行的实验结果如表1所示,其中:A1代表HPSO算法;A2代表SADPSO算法;A3代表IHPSO算法。TSP问题中Bumal14简称问题1;Oliver30简称问题2;Eil51简称问题3;St70简称问题4; Rat99简称问题5;Chl30简称问题6;Chl50简称问题7。 表1中,实际最优解表示相应类别TSP问题的真实情况下的最优路径长度。计算最优解与计算平均值为表中各算法在数据集上运行30次后的最短路径与平均路径长度。在不同数据集使用HPSO、IHPSO与SADPSO算法,发现本文提出的IHPSO算法的最优解更接近真实最优解,并且标准差更小,平均值更接近最优值。说明本文方法能较好地求解TSP问题,计算出的结果较平稳,波动小。由表1中数据可得,本文提出的对策IHPSO算法明显优于HPSO算法与SADPSO算法。 验证本文算法迭代时的收敛过程,并对比IHPSO与人工免疫算法(AIA)在Eil51测试数据上的收敛过程,如图2所示。IHPSO算法在Eil51数据集上的路径优化如图3所示。 表1 HPSO、SADPSO、IHPSO算法求解TSP问题的结果对比 图2 IHPSO与AIA在Eil51测试数据上的收敛过程 由图2可知:IHPSO算法前100代收敛速度较快,由于前100代中每个粒子到最优粒子的汉明距离较大,因此粒子速度大,位置更新的幅度大,收敛速度较快,约300代时算法获得最优解;而AIA受选择、变异的影响,增大了粒子下一代遗传的不确定性,导致收敛速度变慢,在500代左右才收敛到最优解。IHPSO加入了免疫思想,在算法的收敛精度与收敛速度方面都有较大提高。 图3 IHPSO在Eil51数据集上的规划路径 本文提出的算法引入汉明距离,改变了粒子位置和速度的更新方式,弥补了传统粒子群算法不能求解离散问题的不足,并引入免疫疫苗、免疫选择等免疫思想,加快粒子的收敛速度,得到了全局最优解。算法实验分2部分,第一部分比较了IHPSO算法与HPSO、SADPSO在TSPLIB测试集上的实验效果,发现IHPSO算法能获得最优解,并且计算结果浮动范围相比其他2种算法小。第二部分验证IHPSO算法的收敛速度,对比AIA算法在Eil51测试集上的实验效果,发现IHPSO算法较AIA算法提前100代得到最优解,表明 IHPSO算法收敛速度较快。3 改进型粒子群算法

4 实验结果与分析

5 结束语
