建设期高层建筑物沉降数据回归分析方法

张 宇

(铁正检测科技有限公司 山东济南 250014)

1 引言

随着城市高层建筑物的不断发展及社会对结构物安全的重视，高层建筑物沉降变形监测工作已十分重要，对建设期高层建筑物进行持续规范地监测并对其沉降观测数据进行科学有效的计算与分析，能够为建筑物在建设期和使用期的安全提供预警。对于沉降观测数据的科学分析和预测方法，通过认真分析文献资料[1-8]，未见与本文所介绍对沉降数据进行回归分析方法相同的内容。

2 工程概况

某8#建筑物，设计地上建筑为28层、地下-2层，高88.6 m，单体建筑、框剪结构，抗震烈度7度。为保证该建筑物在建设和使用期安全，受开发商委托，特对该建筑物在施工建设期间进行了沉降变形观测。自2016年9月20日至2018年9月10日(历时720 d)，对8#建筑物4个监测点(J1～J4)进行了19期沉降观测，观测数据整体趋势平稳，现任意取一点的沉降观测数据(见表1)作为代表性点位进行分析。

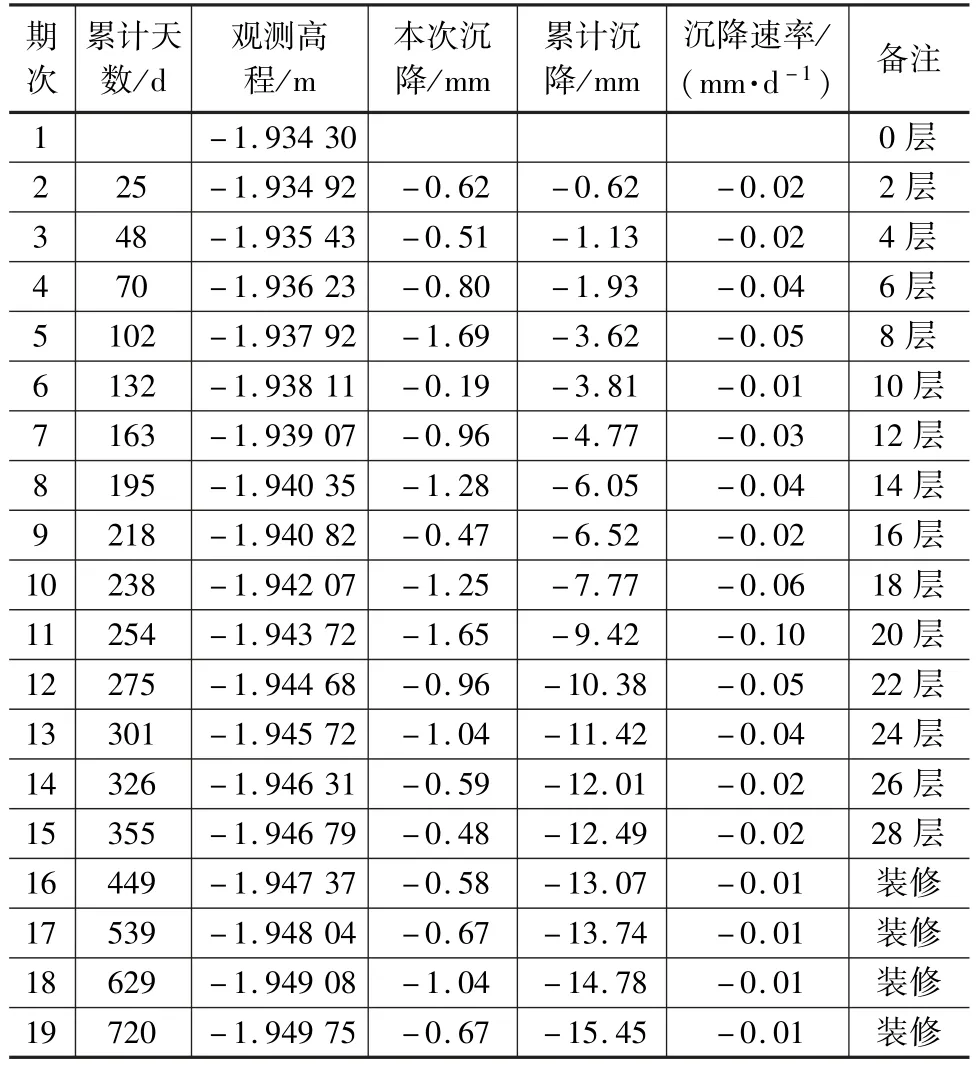
表1 J2点沉降观测数据统计

3 数据分析

3.1 数据检验

为了将沉降观测数据中有异常、含粗差的数据剔除，现采用基于经典统计假设理论的统计检验方法[9](趋势法)对沉降观测数据予以检验。

所谓趋势法，就是对一系列位移时间数据y，假设是以第i点为中心，时间半径为t的所有邻域点的加权平均值(i点除外)，其权可取时间平方的倒数，则有：

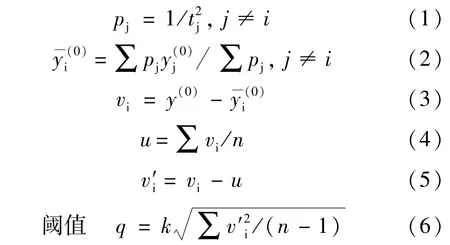
其中，n为邻域中点的数目(i点除外)；大于q的v的观测值，就认为其为异常值，需要剔除；i点的邻域半径t可自行选择，一般不宜太小或太大；k为系数，一般取2.0～3.0。此方法对一些孤立出现的粗差剔除比较有效。

结合表1，选取第5～13期数据进行检验，以第9期数据为i点，时间t为相邻两期时间间隔。

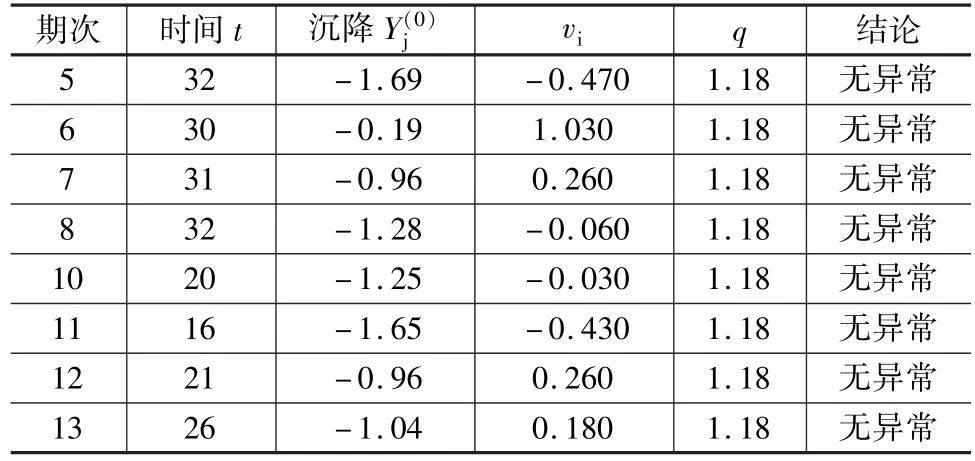
表2 数据趋势法分析

表2中q值计算时k＝2.5，通过第5～13期沉降观测数据分析，未发现数据异常情况，其数据可以作为后续数据回归模型的建立。

3.2 绘制数据散点图

从图1中可以看出，沉降位移yi与时间t呈现非线性关系更加显著，比简单的一元线性关系更切合实际。

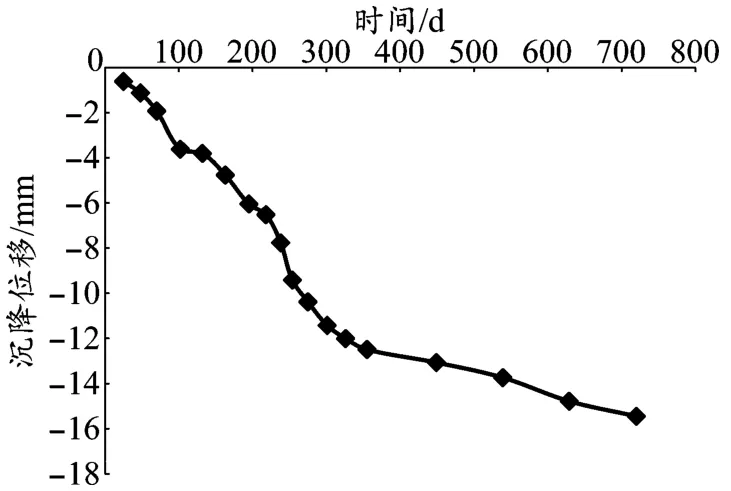
图1 沉降数据散点图

4 回归计算

对建筑物沉降数据进行建模分析，能很好掌握其变形规律以及对其后期变形进行及时预测预报。所谓建模就是对数据进行曲线拟合，也叫曲线回归，回归方法有多种，包括线性回归、多项式曲线回归、e指数曲线回归、对数曲线和双曲线回归等。结合沉降数据散点图(见图1)线型，下面选择多项式曲线和对数曲线模型进行非线性回归计算分析[10-15]。

4.1 回归模型

4.1.1 多项式曲线模型(取至二次方)

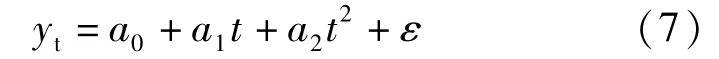
为方便后面计算分析，可以对式(7)进行简化变换，即令t1＝t，t2＝t2，则式(7)变换为多元线性回归模型，即：

4.1.2 对数曲线模型

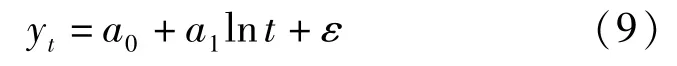
同理，令t1＝lnt，则式(9)变换为一元线性回归模型，即：

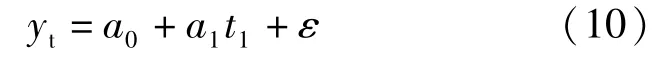
式中，yt为累计沉降量，是预测对象，称为因变量；t为时间(累计天数)，是影响因素，称为自变量；a0、a1、a2为待定的回归系数；ε为残差，是随机误差，其相互独立且服从正态分布N(0，δ2)。

4.2 模型比较

将变换所得回归模型式(8)和式(10)矩阵化，即：

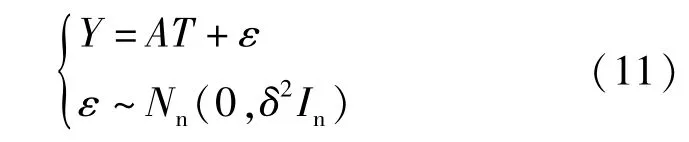
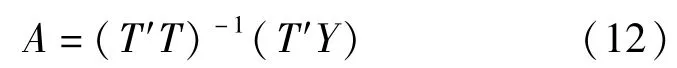
代入数据，分别得到各曲线模型方程，即：

(1)多项式曲线模型方程

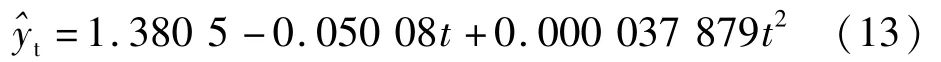
(2)对数曲线模型方程

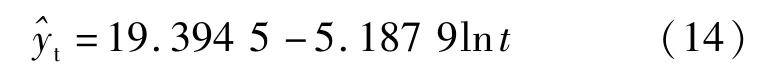
根据各模型方程分别计算J2点沉降预测值(见表3)。从表3中残差值可以看出，其数值均很小且服从正态分布规律，同时从所计算残差平方和可知，本案例沉降数据回归模型方程中，多项式曲线模型方程较对数曲线模型方程回归效果好，同时从预测对比散点图(见图2)也可佐证。

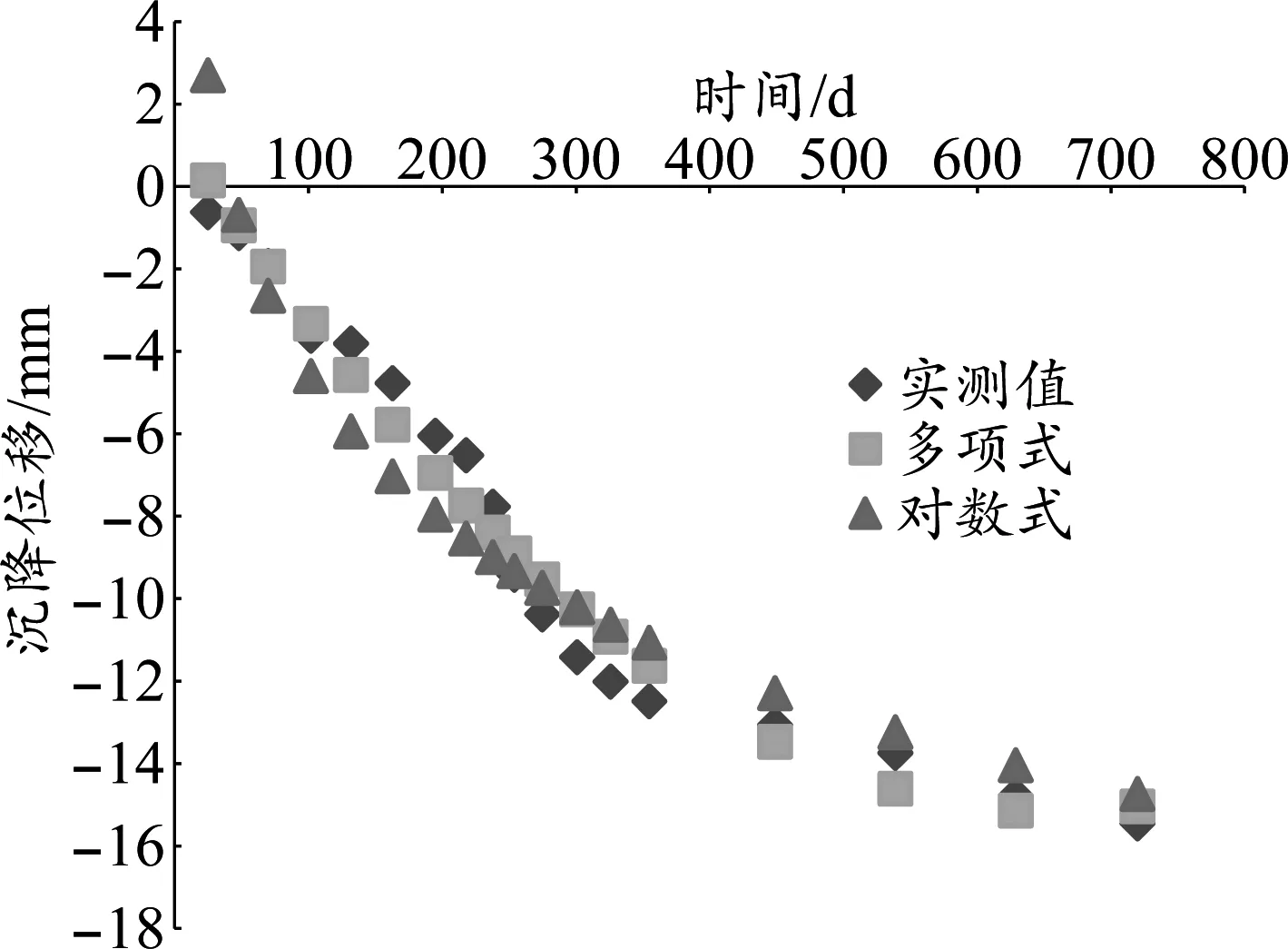
图2 预测对比散点图

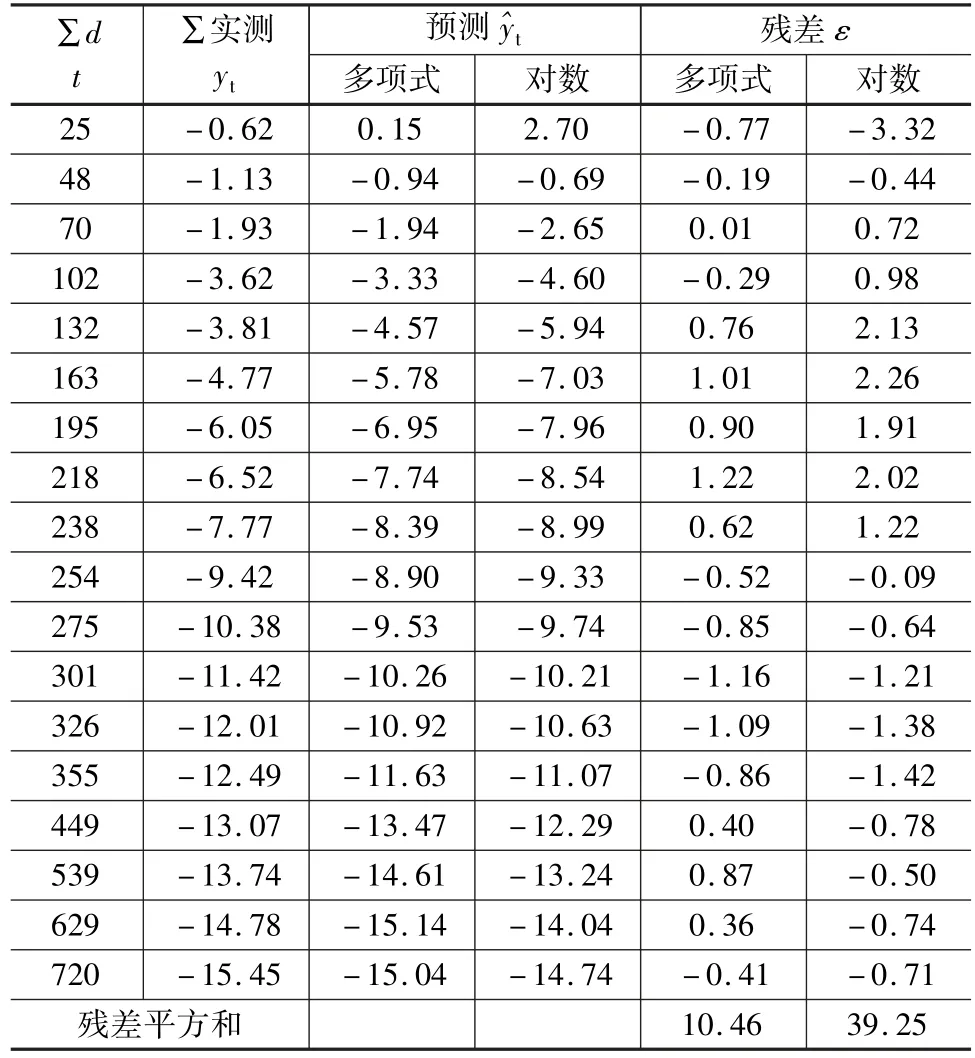
表3 J2点沉降预测比较

下面将对多项式曲线回归模型方程式(13)继续进行检验和分析。

5 模型检验

5.1 回归方程显著性检验

对多项式曲线模型方程，将式(13)变换成式(8)型式，按多元线性模型进行检验。即：

假设H0：ai＝0(i＝1，2)

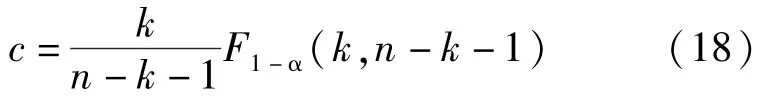
即c＝0.491＜37.557，故拒绝H0，则回归方程式(13)在α＝0.05下呈显著性特征。

5.2 回归系数显著性检验

虽然前面检验了回归方程的显著性，但是每个ti对yt的影响作用并不是一样的，因此需要从回归方程模型中剔除影响不显著的系数项，保留那些比较重要的因素，以便更利于实际应用。同理，将式(13)变换成式(8)型式，按多元线性模型进行检验，即：假设H0：ai＝0(i＝1，2)。

取显著性水平α＝0.05，查F分布表得：

F1-α(1，n-k-1)＝F0.95(1，15)＝4.54

而拒绝域临界值为：

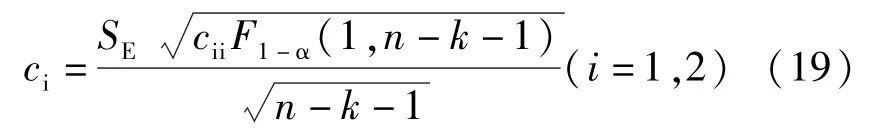
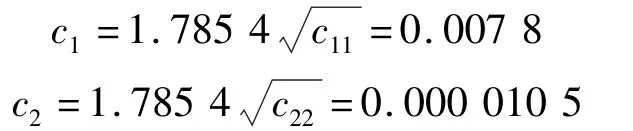
6 模型预测区间估算

对模型式(13)可以求取其在t处的预测区间，即：

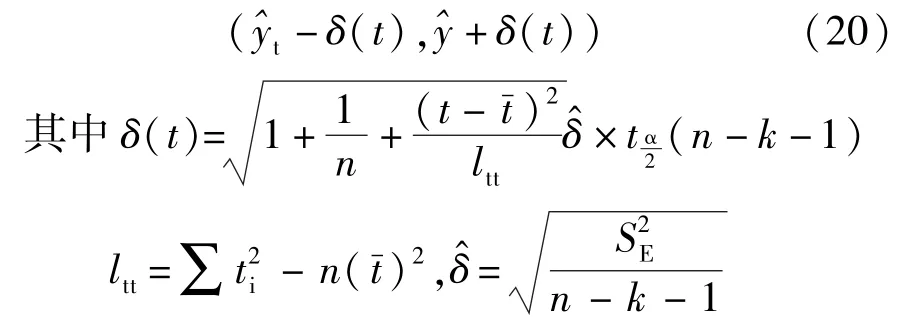
现在选择表3中残差ε最大值所对应的t处作预测区间计算，即求其在t＝218处yt的预测值与置信度为95%的预测区间。代入数据，则有：

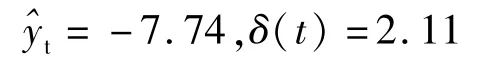
则在t＝218处，yt的预测区间为(-9.85，-5.63)，从表3中其实测值和预测值看，均符合预测区间值。

同理，可求得t在其他处时yt值预测区间。

7 结束语

对8#建筑物代表性沉降观测点J2，作者此前曾对其观测数据进行过一元线性回归分析，其残差平方和为51.7，本文又进行了多项式和对数曲线非线性回归计算，通过比较残差平方和(见表3)，发现本文所述两种非线性回归较一元线性回归效果好，多项式回归又较对数曲线回归效果好。因此，对建设期高层建筑物沉降数据进行回归分析，应采用多种回归模型进行计算比较，从而选择最优模型进行其他沉降数据和后期变形情况的预测与分析。

同理，也可以结合竣工后的更多沉降观测数据，利用本文所述回归模型计算的方法，对建筑物在今后使用过程中一定阶段的沉降总值及变形趋势进行进一步预测计算和评估分析。