半监督平衡化模糊C-means聚类
2019-05-22朱乐为胡恩良
朱乐为,胡恩良
(云南师范大学 数学学院,云南 昆明 650500)
聚类的目的是发掘样本的类别标记,进而根据类标记揭示数据的内在结构和规律.在聚类分析中,样本的类别标记信息未知,故聚类分析属于“无监督”学习方法.随着聚类分析的发展,涌现出了多种优秀的聚类算法,其中FCM[1](fuzzy C-means clustering)是一种被广泛应用的聚类算法.FCM作为K-means[2]的变体,在硬聚类的基础上引入了模糊理论,在实际运用中获得了极大成功.
然而,对于非平衡数据,FCM的聚类效果并不理想.非平衡数据是指不同簇(类)所含样本点数相差较大的数据集.其中,样本数少的类称为小类,样本数多的类称为大类.对于不平衡数据的研究首先源于有监督机器学习分类,目前为止已产生了大量的研究成果,提出了许多富有成效的处理方法.主要包括:① 数据集的重构,即通过欠采样[3]或过采样[4]将不平衡数据集转换为平衡数据集;② 分类器算法[5]的修正,即对分类器权重进行调整,使之对少数类敏感.在模糊聚类领域(无监督分类)也存在着非平衡数据聚类问题,但是到目前为止,仅有少量研究对非平衡数据问题进行探讨.Noordam等[6]提出一种对聚类尺寸不敏感的模糊C-means算法,其方法是对于小类与大类设置不同的条件值;Wen等[7]提出广义均衡FCM聚类算法,改进了原FCM属度表达式以抵消相异簇大小差异对聚类结果的影响.
上述方法可以在一定程度上解决非平衡问题,但也存在着一定的缺点:① 条件值为人为设定,不一定有利于聚类任务,在处理类较多的不平衡数据集时,该方法使得样本对各个类的隶属度都较小,减弱了算法的聚类能力;② 广义均衡FCM算法在模糊指数m=1时无法判断隶属度系数迭代方程可解,不能保证通过交替迭代收敛到稳定点.除以上2点外,传统的聚类算法属于无监督学习方法,没有利用监督信息,可能会产生聚类偏差.而在现实的聚类任务中,通常能获得一些额外的先验信息,如部分样本已带类标记.充分利用已知的部分标记来协助聚类,能得到更好的聚类效果.
基于以上分析,本文提出一种半监督的平衡化FCM聚类算法(简记为SBFCM),该算法在原FCM目标函数的基础上引入对聚类模糊隶属度矩阵的近似正交约束和半监督约束,其作用是:① 近似正交约束项迫使隶属度矩阵近似正交,由此可根据簇的大小自动调整数据点权重,这将增强聚类效果;② 半监督约束则能够利用已知的部分标记信息来引导聚类.实验表明,SBFCM能够较好地解决数据的类不平衡问题和有效利用部分标记问题,可提高聚类精度.
1 平衡化模糊C-means聚类
1.1 模糊C-means聚类分析
FCM聚类 (fuzzy C-means clustering)方法作为C-means聚类的一种变体,它基于模糊划分理论,通过优化求解模糊隶属度矩阵来获得数据点的类别标签.对于FCM,其目标函数形式如下:
(1)
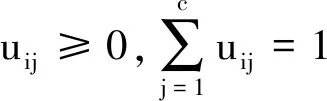

则式(1)退化为C-means的目标函数.由此可知,FCM是对C-means的“软化”.

(2)

(3)
1.2 模糊C-means聚类中的“均匀效应”
FCM聚类方法在处理不平衡数据集时会倾向于产生大小相同的类(簇),极易导致错误的类(簇)划分,该现象称为“均匀效应”.2012年,Xiong等[9]对“均匀效应”的成因进行了系统地分析:若假定数据集仅含2个类(簇),则式(1)可改写为:
(4)
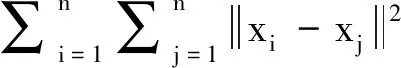
(5)
(6)
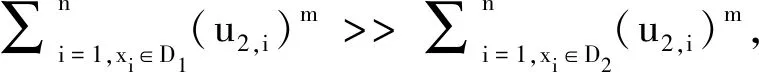
这意味着若初始值差异较小,则v1,v2会随着迭代次数增加趋向于重合,“均匀效应”愈发明显.
1.3 平衡化模糊C-means聚类算法
在FCM中,隶属度系数的单纯形约束条件为
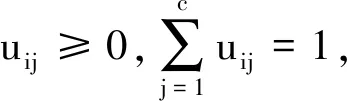
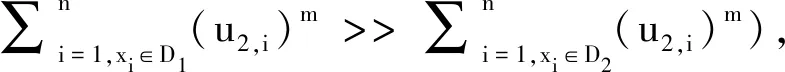

(7)

(8)
在式(7)中,每个类(簇)所含样本的隶属度平方总和近似相等,这保证了各类间隶属度总和的平衡.例如,设W=[wij]为原始隶属度矩阵,考虑第p和q两个类(簇),设第p类(簇)所含样本数远大于第q类(簇)所含样本数.若将W近似正交化变为U,即W→U且UTU≈I,则第i个样本点属于类(簇)p的隶属度变为:

基于以上分析,将隶属度矩阵的近似正交约束项融合到FCM目标函数中,得到了平衡化模糊C-means聚类模型(BFCM)如下:
(9)
其中γ≥0为正交约束参数.对比式(1)和式(9)可知,BFCM在FCM的基础上要求隶属度矩阵近似正交,在FCM目标函数与隶属度正交约束之间达到折中,以此解决非平衡数据上的聚类问题.
2 半监督平衡化模糊C-means聚类
2.1 模型建立
传统的聚类属于无监督学习,未能利用已有的先验信息(也称为半监督信息).但在现实中,通常能事先获得部分类标号信息,利用该信息可改善聚类效果.受文献[12]启发,我们在模型(9)的基础上进一步引入少量类标记数据作为先验信息,即对隶属度矩阵融入了半监督约束项,得到半监督平衡化模糊C-means聚类(SBFCM)模型如下:

(10)
其中,yij为样本xi属于第j类的类标号,若该标号已知,则yij=1,否则yij=0.特别地,若yij=0,∀i,即表示没有任何先验类标号可用,此时SBFCM退化为BFCM.
2.2 SBFCM模型求解
由式(10)可知,SBFCM的目标函数为双变量非凸函数,适合利用EM算法进行交替优化求解.求解SBFCM中心更新公式,对vj求偏导可得:
令

化简可得vj的闭式解为

(11)
另一方面,式(10)关于U的表达式较为复杂,不易求出uij的闭式解,故本文在EM迭代中采用投影梯度下降法求解隶属度矩阵U.EM交替求解V和U可产生如下迭代序列:
V(0)→U(1)→V(1)…→U(t)→V(t)→…
该求解过程可整理成算法1.
算法1SBFCM求解算法
输入部分类标号yij,类别数c,平滑指数m,正交约束项系数γ,最大迭代次数T,终止阈值ε;
repeat
Step 1 利用投影梯度下降法求解隶属度矩阵

.
Step 2 更新聚类中心:
Step 3t=t+1
until
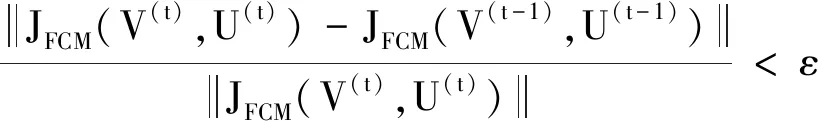
输出U=U(t).
3 实验与分析
3.1 数据集与聚类评价
本文共采用了9个数据集进行试验,它们分别是sonar,chessboard,spiral,heart,iris,wine,soybean,glass和protein,均来自于UCI数据集,其信息详细见表1.其中,soybean,glass,protein为非平衡数据集,其余为平衡数据集.

表1 数据集及其信息
聚类性能评价指标通常分为2类:一类是将最终的聚类结果与某个给定的参考模型进行比较,称为“外部指标”,例如聚类纯度[13](cp,cluster purity),jaccard系数[14]等;另一类是不利用任何参考模型而直接考察聚类结果,称为“内部指标”,例如DB指数[14](davies-bouldin index),Dunn指数[14](dunn index)等.由于本文所采用表1中数据集的真实类标记已知,故我们将真实类标记作为标准参考模型,然后将聚类纯度作为评价指标,其定义如下:
(12)
其中n为数据集中的样本总数,njl为在参考模型中属于第j类的样本但被算法聚类为第l类的样本数量.聚类纯度指标的设计思想是:对于参考模型中的每一类,选择聚类后含该类标记样本数最多的簇作为该标记对应的聚类,每个聚类中与类标记相同的样本点数相加,除以总样本数,即为聚类纯度.
聚类实验将FCM、BFCM和SBFCM 3种方法进行对比,利用各自输出的聚类纯度来比较各个方法的聚类性能,聚类纯度越高,对应的方法越好.
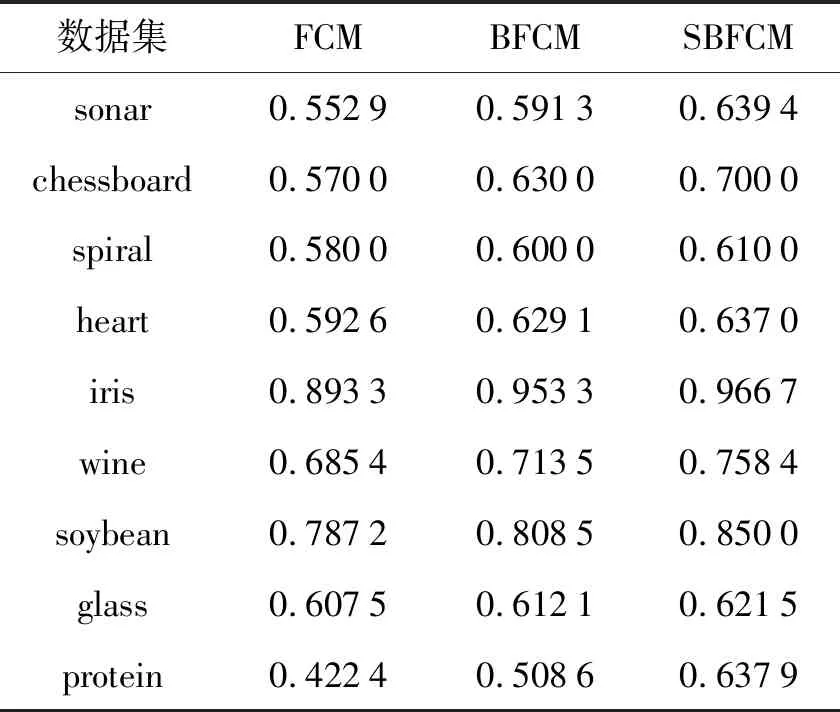
表2 FCM、BFCM和SBFCM获得的聚类纯度对比
3.2 聚类效果分析
表2的第2列、第3列和第4列分别给出了FCM、BFCM和SBFCM方法输出的聚类纯度,对SBFCM算法,在实验中随机抽取10%的真实类标记作为监督信息.3者对比聚类纯度最大者用粗体字显示,从中可看出.
1) BFCM在9个数据集上的聚类纯度均高于FCM,在数据集chessboard, iris和protein上的优势尤其显著,其原因是:BFCM在FCM的基础上加入了近似正交约束项,这使得大类的样本隶属度降低,小类样本的隶属度升高,从而抑制不同类(簇)中心点相互靠近,缓解了“均匀效应”.此外,近似正交约束能使不同类(簇)样本的隶属度成近似正交关系,提高了类(簇)间的分离性.
2) SBFCM在9个数据集上的聚类纯度均高于BFCM,在数据集chessboard, soybean和protein上的优势尤其明显,其原因是:SBFCM在BFCM基础上加入了半监督约束项,利用少量已知的先验类标记信息来引导聚类,从而提高了聚类效果.
3.3 监督信息量对聚类效果的影响
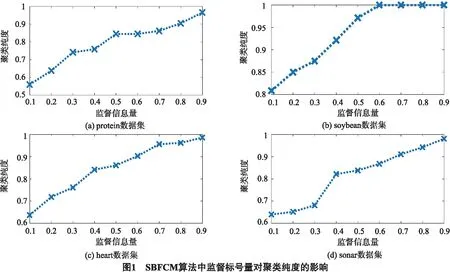
为了考察不同监督规模对SBFCM的影响,在数据集protein, heart, soybean和sonar上,图1给出了SBFCM随监督信息量变化的聚类纯度图.在图1的各子图中,横轴表示给定的类标记数相对于总样本数的比重,纵轴表示获得的聚类纯度.从4个子图可以看出,随着监督标记量的增加,SBFCM获得的聚类纯度也相应提高.特别地,对soybean数据集,当监督标记量为60%时,获得的聚类纯度已达100%.
4 结语
为探讨在非平衡数据上的聚类问题,本文在FCM的基础上提出了平衡化模糊聚类模型BFCM;为了进一步利用已知类标号更好地引导聚类,本文进而提出了半监督的平衡化模糊聚类模型SBFCM.SBFCM在FCM目标函数的基础上加入了对聚类模糊隶属度矩阵的近似正交约束和半监督约束,从而得到了新的聚类目标函数.在9个标准数据集上的实验结果表明,相比于FCM和BFCM,SBFCM具有更好的聚类效果.在未来的研究中,我们将进一步探讨如何更优地选取SBFCM中的模型参数.

