基于模糊度的决策树生成算法

罗秋瑾

(云南财经大学 统计与数学学院,云南 昆明 650221)

由于在实际问题中充斥着大量的不确定性，使用传统的决策树难以从不确定性问题中获取到有用的信息，所以需要对传统的决策树进行推广，推广以后得到的模糊决策树，主要用于处理这些不精确的信息.

由ID3算法扩展得到的Fuzzy-ID3算法[1]是模糊决策树归纳算法的典型代表，它主要是依据平均模糊分类熵选择扩展属性，利用模糊置信度作为判断模糊决策树叶子结点的终止条件．除此以外，常用的模糊决策树算法还有Yuan[2]和Yeung等[3]提出的启发式算法，这些算法都有一个共同的特点就是需要对条件属性值进行模糊化处理，而任何形式的模糊化都不可避免地会造成信息的丢失，从而造成信息的失真.此外，依据模糊依赖度选择扩展属性，也是比较常用的一种启发式算法[4-5].

但是，由于粗糙模糊依赖函数不是单调地，也就是说较少的条件属性也有可能计算出较大的依赖函数值，从而导致算法有不收敛的可能[5]，基于上述问题，提出了一种改进的模糊依赖函数作为启发式选择扩展属性，再利用模糊粗糙度作为叶子结点的终止条件.从而可以使得该归纳算法具备很好的收敛性.

1 基本概念

1982年波兰科学院院士Pawlak教授[6-7]提出的粗糙集理论是处理知识中的不确定性的有力的工具.模糊粗糙集理论和方法是由D.Dubois和H.Prade在1990年提出的数学理论，用于处理数据类型中存在的不一致性的.

模糊粗糙集的特点是将粗糙集和模糊集同时进行了集成扩展，使得它既可以处理数据中的模糊性又可以处理数据中的粗糙性.发展到现在，它已经基本建立起了一个完备的理论框架，在理论方面和应用方面都取得了相当丰富的研究成果，在数据挖掘等领域有着较为广泛的应用[8-9].

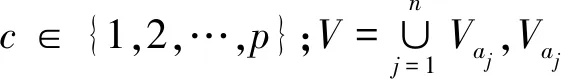
定义2给定模糊信息系统FIS=(U,A∪C,V,f)，P为定义在论域U上的模糊等价关系，X是定义在U上的模糊集.对于给定的x∈X，X的P模糊下近似和X的P模糊上近似分别定义为：

(1)

(2)

定义3给定模糊信息系统FIS=(U,A∪C,V,f)，P∈A，Q∈C. 对于给定的对象x∈X，定义对象x属于模糊正域的隶属度定义为[11]：

(3)

定义4给定模糊信息系统FIS=(U,A∪C,V,f)，P∈A，Q∈C.模糊条件属性P相对于模糊决策属性Q的依赖度定义为

(4)

其中，|U|表示论域中包含对象的个数.

2 改进的模糊决策树归纳算法

通常模糊决策树的生成主要包含2个步骤，一个是扩展属性的选择，以此为标准做启发式算法，另一个则是树的终止条件，否则会造成过度拟合的情况，通常归纳算法都是围绕这两个问题展开，其中以扩展属性的选择这一步最为重要，也就成为了算法的核心.

2.1 对原算法的一些分析

文献[12-13]中翟俊海等提出的粗糙模糊决策树归纳算法中，用定义4给出的模糊条件属性P相对于模糊决策属性Q的依赖度τP(Q)作为标准选择扩展属性，但是文献[5，10]指出此依赖函数τP(Q)不具备单调性，也就是说少的条件属性可能计算出大的依赖函数值，从而导致算法有不收敛的可能.

基于上述问题本文提出了一种改进的依赖函数作为启发式选择扩展属性.

定义5给定模糊信息系统FIS=(U,A∪C,V,f)，P∈A，Q∈C. 对于给定的对象x∈X，对象x属于模糊负域的隶属度定义为

(5)

定义6给定模糊信息系统FIS=(U,A∪C,V,f)，P∈A，Q∈C.模糊条件属性P相对于模糊决策属性Q的依赖度定义为

(6)

γP(Q)的值越大，说明条件属性P相对于决策属性Q就越重要.因此用γP(Q)作为选择扩展属性的启发

式算法.

定义7给定模糊信息系统FIS=(U,A∪C,V,f)，P∈A，Q∈C. 修改模糊条件属性P相对于模糊决策

属性Q的模糊粗糙度定义为：

(7)

在模糊信息系统中，模糊粗糙度刻画的是模糊集的粗糙程度．模糊粗糙度越小，说明对模糊集分类的粗糙性就越小，也就越容易实现分类．所以，本文用βP(Q)作为叶子结点的终止条件．

2.2 改进算法

输入：模糊信息系统FIS=(U,A∪C,V,f)，阈值参数λ.

输出：模糊决策树

Step 1 对每一个条件属性ai∈A，用式(6)分别计算决策属性C相对于条件属性ai的模糊依赖度；

Step 2 根据模糊依赖度的取值，选择依赖度值最大的条件属性a0作为扩展属性，即：

Step 3 用式(7)计算出a0各个分支的模糊粗糙度βaij(C)，如果存在aij，使得βaij(C)>λ，则产生一个叶子结点；否则，重复第1至第3步骤；

Step 4 输出模糊决策树.

3 实例说明

表1 模糊决策表

在表1所示的Ⅰ-型模糊决策表中，U={x1,x2,…,x16}，A={a1,a2,a3,a4}，其中a1={a11,a12,a13}，a2={a21,a22,a23}，a3={a31,a32}，a4={a41,a42}.

对于决策属性C，U/C={C1,C2},其中，C1={x2,x4,x5,x12,x14,x16}；

C2={x1,x3,x6,x7,x8,x9,x10,x11,x13,x15}.

Step 1 先计算决策属性C对条件属性ai(1≤i≤4)的模糊依赖度，以a1为例：

μNEGa1(C)(x1)=μNEGa1(C)(x3)=μNEGa1(C)(x4)=μNEGa1(C)(x5)=μNEGa1(C)(x9)=μNEGa1(C)(x11)=0.7,

μNEGa1(C)(x2)=0.6,μNEGa1(C)(x6)=μNEGa1(C)(x10)=μNEGa1(C)(x15)=0.3,μNEGa1(C)(x7)=0.1,

μNEGa1(C)(x8)=μNEGa1(C)(x12)=μNEGa1(C)(x13)=μNEGa1(C)(x14)=0.9,μNEGa1(C)(x16)=0.5.

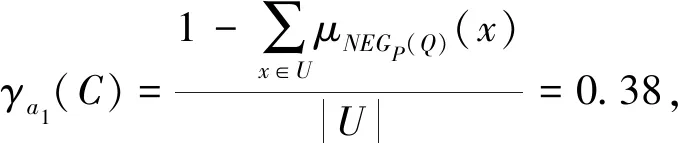
Step 2 因为条件属性γa1(C)的值最大，所以条件属性a1(Outlook)被选为扩展属性，即模糊决策树的根结点.

Step 3 根结点Outlook有3个分支：Sunny，Cloudy和Rain.计算3个分支相对于C1，C2的模糊粗糙度：

在分支Rain，相对于C2的模糊粗糙度是0.91，超过了阈值λ=0.85，所以终止于C2，属性决策值为No的叶结点.

在分支Sunny, Cloudy处重复过程，可从表1生成一棵模糊决策树.

Step 4 输出模糊决策树.如图1所示.

4 结语

针对模糊信息系统，提出了一种新的模糊决策表归纳算法，该算法重新定义了模糊决策属性相对于条件属性的模糊依赖度和模糊粗糙度，以模糊依赖度作为选择扩展属性的依据，以此为标准生成模糊决策树启发式算法，再利用模糊粗糙度作为叶子结点的终止条件.最后用实例说明该算法生成的决策树较为简化，且不会造成信息丢失，并且算法收敛性也较好.本文后续工作将研究把决策表的属性约简引入到决策树的生成过程中，以简化在条件属性较多的情况下，简化树的生长过程.