基于TBR模型的高水头混流式水轮机水力性能预测

2019-05-21孙龙刚郭鹏程郑小波罗兴锜

农业工程学报 2019年7期

孙龙刚，郭鹏程，麻全，郑小波，罗兴锜

（西安理工大学水利水电学院，西安 710048）

0 引言

动静干涉（rotor-stator interaction，RSI）现象是叶轮机械的显著特征，主要是由于转子与定子的相对运动，前排叶片的尾迹区对后排叶片形成周期性扰动，引起叶轮内部速度及压力场随时间发生周期性变化，诱导幅值较高的压力脉动[1-3]。Franke等澄清了RSI的产生机理，首次对 RSI作用下的压力波模式进行了可视化研究，并对一个20个活动导叶的水泵水轮机进行了试验验证[4]。叶轮机械 RSI效应的捕捉，必须进行瞬态计算，而为了避免共振，叶轮机械转子与定子叶片数往往互质，使得周期性边界条件设置失效，此时必须对整圈叶片进行计算，保证转子与定子之间的螺距比为1，从而确保上下游信息的准确传递，以提高计算精度[5]。江伟等[6]研究发现，随着流量增加，离心泵半高导叶断面间隙对叶轮和导叶之间的 RSI作用逐渐减弱，而叶轮与蜗壳之间作用逐渐增强。李伟等[7]采用PIV技术对混流泵内部流场进行了试验研究，测试结果显示受叶轮和导叶之间 RSI作用的影响，导叶进口处涡旋流动结构较为明显，造成流道堵塞。麻全[8]数值研究了高水头混流式水轮机稳定飞逸工况下水轮机不同位置的压力脉动特性及 RSI效应。叶轮机械全流道数值计算相当耗费计算资源及时间，并且与计算域的离散、湍流模型，求解控制等均有关。水轮机部件相对较多，为更准确地捕捉内部流动特性，全流道计算的网格已达上千万甚至更多[9]，而进行全流道瞬态计算，单个工况的计算时间通常要达数十天，若采用更高级的湍流模型及要求更高精度，时间会更长且消耗更多的CPU及内存[10-11]。

TBR（transient blade row）模型[12]提供了一种采用1个或者 2个流道计算叶轮机械瞬态效应的方法，并且保证一定的精度，从而解决了瞬态计算部分流道相邻级之间角度比不为 1的问题，大大降低了叶轮机械瞬态分析的计算资源与时间消耗，使得瞬态分析能够成为叶轮机械常规设计的有力工具。TBR模型提供了3种方法：PT（profile transform）法，TT（time transform）法和 FT（fourier transform）法[13]。PT法是最直接的变换法，是将分布在交界面上的变量按照角度比进行比例缩放从而保证通量守恒；TT法基于时间倾斜法，是一种显示计算；而 FT方法采用傅里叶级数对周向边界和转静边界进行求解历史的重构[14-15]。Zori 等[16]分别采用TT方法和PT方法对某一1.5级跨声速压缩机进行了数值模拟，对比分析不同方法的在气体动力学参数及内部流动特征的捕捉能力。Connell等[17]分别以高压动力涡轮级和低压飞机涡轮级为研究案例，在计算资源的优化利用以及时间精度上对比分析不同参数对PT法、TT法以及FT法的影响，结果表明，TT法与FT法在时间精度上要高于PT法，而FT法在稳定性上要强于TT法。Robinson等[18]利用TT法对某一带导叶扩压器的离心压缩机进行了数值计算，获得了与试验值比较一致的数值解。Cornelius等[19]评估了稳态计算方法和瞬态的 TT法在多级轴流压缩机旋转失速点捕捉和气体动力稳定性预测的可靠性，与稳态计算比较，在接近失速区瞬态的 TT方法获得了与试验数据更匹配的速度线。此外，TT方法与FT方法还可应用于进口扰动、叶片颤振等。

目前TBR模型多用于涡轮机及压缩机的性能预估及负荷预测上，且多用于可压缩流动，而以水为工作介质的叶轮机械具有大密度特性，其动态液体力更大，RSI效应将更为显著。2014年，挪威科技大学（Norwegian University of Science and Technology-NTNU）公布了名为Francis99（又名 Tokke模型）混流式模型水轮机的几何模型，同时提供了详细的水力效率、压力脉动等试验数据，便于对数值计算进行验证、分析及比对[20-21]。Nicolle等[22]采用 TBR模型对 Francis99高水头水轮机进行了性能预测，该文的计算结果表明压力脉动幅值沿流线方向依次减小，与试验结果差异较大。与Nicolle等的计算方法不同，本文采用不同的模拟域并重新生成高质量的网格，分别利用全通道方法、PT方法与FT方法对Francis99模型水轮机进行不可压缩的RSI及叶片负荷数值预测，并与试验值结果进行对比，以评估PT方法及FT方法在预测以水为工作介质的不可压缩叶轮机械性能的可靠性。

1 计算理论及模型

1.1 流动控制方程及k-ω SST模型

非稳态的 RANS（Reynolds Average Navier-Stokes equations）方程如下[23]

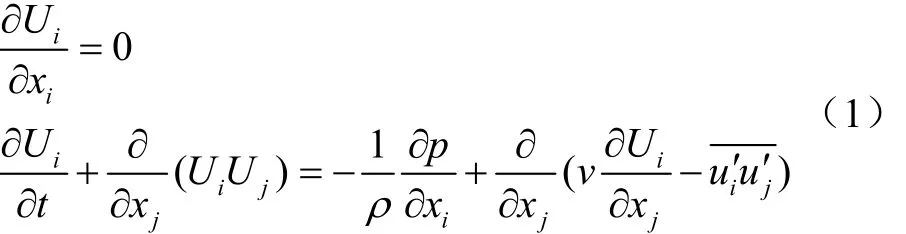
式中t为时间，s; ρ为密度，kg/m3；p为压力，Pa；v为涡黏度；Ui与Uj分别为i和j方向上的时均速度，m/s;ui′和u′j分别为脉动速度，为Reynolds应力张量。

本文采用k-ω SST湍流模型来封闭方程组（1）。

式中vt表示湍动涡黏度，为待求量，Sij为变形率张量，δijk为Kronecker符号。

k-ω SST湍流模型中湍动能k和比耗散率ω的输运方程如式（3）所示[24]

式中F1与F2为混合函数，Pk为湍动生成项，α，α1，β，β*，σk，σω，σω2等均为方程组闭合系数。

k-ω SST湍流模型在边界层使用k-ω湍流模型，在其余区域应用k-ε湍流模型，可较好地捕捉叶轮机械的流动分离现象。

1.2 TBR模型

由于TT方法仅仅适用于可压缩流动，故本文只进行了PT法与FT法的数值计算。如图1所示为PT法与FT法原理示意图。

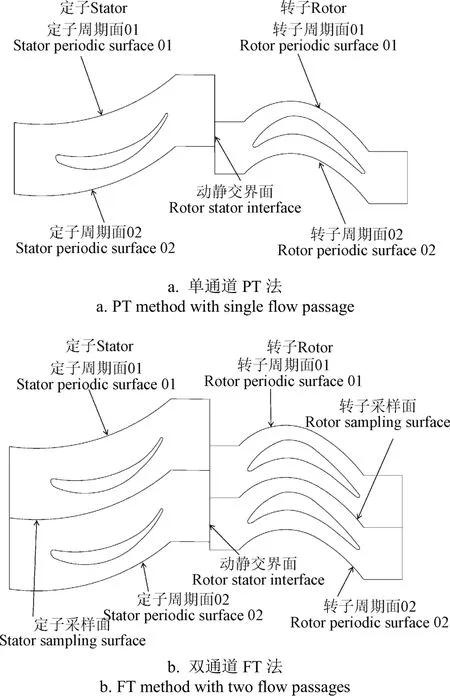
图1 PT法与FT法原理示意图Fig.1 Principle diagram for profile transform (PT) and Fourier transform (FT) methods

如图1a所示，PT方法是最简单最直接的方法，其原理是按照式（4）对变量进行缩放，从而达到上下游通量守恒的目的，但是其对角度比有严格的限制，要求接近1。

式中1pφ与2pφ分别为交界面上游及下游通量，l为角度比。

FT方法对角度比没有严格限制，使用一种采样方法对求解历史数据进行重构，是将前几次计算生成的数据作为一个采样点用来进行下一次计算，然后对采样点进行傅里叶级数展开，获得所关心的物理量在某一位置上的函数关系式。FT方法采用相变边界条件，其圆周方向在不同时刻彼此成周期。按照式（5）转子与定子在中间面上进行流动变量的采样，从而计算出傅里叶系数[22]，如图1b所示。进一步，FT方法利用基于周向角度差的相角滞后及转轮速度，对周期面上的流动变量用傅里叶系数进行重新构建，如式（6）和（7），因此不用存储完整的计算信号，提高了计算速度。

式中sφ，1pφ，2pφ分别为采样面，2个周期面上的流动变量，t与Δt分别为时间和时间步长，Am为傅里叶系数，m为采样数，ω为角速度，PR和PS分别为一个流道内转子与定子的周向角度，R为半径。

1.3 计算模型及网格生成

Franciss99模型主要部件包括一个内嵌14个固定导叶的蜗壳、28个活动导叶，带有15个长叶片及15个短叶片的转轮及一个弯肘形尾水管。模型机与原型转轮出口直径分别为0.349和1.778 m，两者间的缩放比为1:5.1。最优工况下，模型机组活动导叶开度α为9.84°，试验水头H为11.91 m，转速n为35.12 rad/s，按照IEC 60193，流量系数QED及转速系数nED分别为0.15和0.18，对应的原型机组水头及出力分别为377 m和110 MW[25-27]。

计算域离散采用精度较高的块结构化六面体网格对计算域进行离散，对活动导叶及转轮叶片，整体采用“H”形块，然后在翼型壁面使用一个“O”形块包裹叶片以便提供更好的网格质量，并且对所有的壁面处进行局部加密处理以期望获得更好的壁面求解。采用 5种不同密度的网格进行网格无关性验证，网格总数分别为306.7万、651.2万、960.4万、1 227.9万和1 523.4万，图2所示为水轮机效率及扭矩随网格数的变化规律。由无关性测试结果可知，当网格数大于 960万时，水轮机水力效率与转轮扭矩随网格数的增加不再变化，因此考虑到计算资源与计算精度的折衷，数值计算网格数最终选取为960.4万。如图 3所示为数值计算采用的转轮及活动导叶网格示意图。

数值计算域各过流部件网格信息如下，蜗壳（包括活动导叶）、活动导叶、转轮及尾水管网格的最小角度分别为21.4°，24.7°，28.8°和35.4°，对应的网格纵横比为77、96、242和83，最小网格质量分别为0.32、0.41、0.45和0.62。第一层网格距壁面的距离分别为 0.3，0.1，0.15与0.3 mm，在最优工况计算得到的壁面最大y+值（ y+为第1层网格距离壁面的无量纲距离）分别约为 65、88、67和87，平均y+分别为28、32、16和22。

图2 网格无关性测试Fig.2 Mesh independence test

图3 过流部件网格示意图Fig.3 Grid views of different flow passage components

2 计算工况及设置

在最优工况（best efficiency point—BEP）下分别采用全通道（Full），单流道的 PT方法以及双通道的 FT方法进行水力性能预测，3种不同计算策略模拟域如图4所示。由于Francis99模型转轮为长短叶片形式，转轮一个流道必须包含一个长叶片与一个短叶片，故将 2个活动导叶与一对长短叶片的组合作为PT方法计算域，同理，FT方法计算域为4个活动导叶与2对长短叶片的组合。

图4 三种模拟策略计算域示意图Fig.4 Views of fluid domain for three simulation strategies

首先进行全通道稳态计算，获得一个稳定的初场。数值计算进口给定质量流量，出口指定静压，壁面均采用光滑、无滑移条件。瞬态计算动静交界面为“Transient Rotor Stator”，对流采用高阶求解格式，瞬态模型则采用二阶向后欧拉模式，收敛标准设为最大残差小于0.001。为消除进出口条件不同带来的误差，将全通道提取出的PC（profile boundary conditions）条件作为PT法及FT法的进出口条件，进口为速度矢量，出口为静压，数值计算中仅仅与计算域重合的PC边界条件是有效的。计算过程中，通过设置一系列监测点来动态监测积分变量及压力、速度等值的变化，一方面可以对动量方程提供反馈，另一方面起到诊断计算是否正确的目的。图 5所示为试验装置压力传感器安装位置[23]，数值计算在相同位置布置压力测点以进行验证和对比。

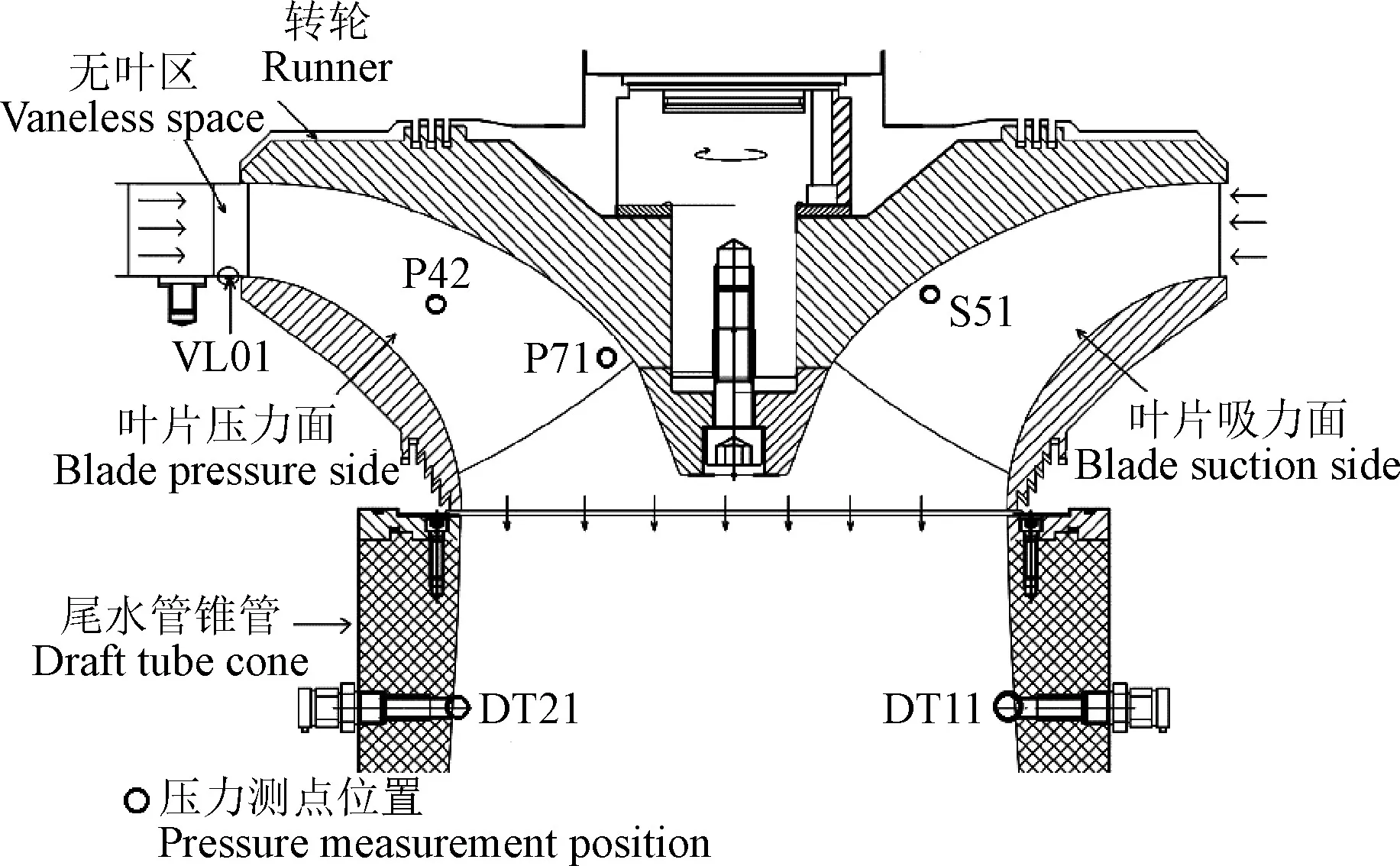
图5 试验传感器与数值监测点位置示意图Fig.5 Locations of experimental pressure probe and monitoring points of numerical simulation

如图5所示，试验测量与数值计算分别进行了6个不同位置的压力测量，其中VL01位于转轮与活动导叶之间的无叶区，DT11和DT21安装在尾水管内，安装位置Z=-0.305 8 m，剩余3个压力传感器P42、P71和S51安装在转轮叶片上，随转轮做旋转运动。其中 P42和 P71在叶片压力面，P42位于叶片中心位置，P71在近叶片出水边且靠近轮毂一侧，S51位于吸力面约叶展2/3、靠近轮毂处。

3 结果与分析

为综合对比不同计算方案在数值计算精度上的预测能力，本文主要从水动力学特性、转轮内部压力负荷分布、时变压力信息及其频谱特性等方面进行分析。在配置相同工作站（戴尔T7910，至强双处理器E5-2680 V3，24核心，内存80G）且计算步数、收敛准则相同的条件下，全通道计算、PT方法以及FT方法计算时间比约为1:0.375:0.23，表明PT法与FT法对计算资源的需求大大减小。

针对Francis99模型，国外进行了一系列的数值及试验研究。Trivedi等[25]对Francis99模型进行了详细的模型试验及数值研究，Lucien等[28]进行了Francis99水轮机部分流道的稳态及全流道的瞬态计算，Buron等[29]采用非线性谐波法模拟了Francis99模型的RSI效应。上述研究获得比较一致的结果为：数值模拟的水轮机水力效率均高于试验值；不同位置测点上的平均压力在转轮与活动导叶之间的无叶区及叶片表面均高于试验值，而尾水管内则低于试验值；测点压力脉动频谱特性方面，叶片正面中心位置测点幅值最高、无叶区次之。本文主要通过与试验数据以及上述研究的计算结果进行对比分析，以评估PT方法以及FT方法在水轮机水力性能预测的可靠性。

3.1 水力效率

水力效率是水轮机整机性能的表征参数，表 1统计了 3种不同计算方法获得的水力效率与试验值，数值效率计算采用进出口总压差法。由效率统计表可知，3种数值方法计算的水力效率均与试验值吻合得比较好，数值解均高于试验值，这是由于数值计算对模型进行了一定的简化，如未考虑转轮上冠和下环的迷宫环密封，未计容积损失、圆盘摩擦损失等。试验效率值为93.4%，全通道方法为94.6%，而PT和FT方法均为95.8%，3种数值计算效率偏差分别为 1.28%，2.57%，2.57%。PT与 FT方法的结果相对于试验测试偏差高于全通道计算，分析认为主要由两种原因所致。一是PT与FT方法仅仅对活动导叶与转轮的部分流道进行模拟，忽略了蜗壳、活动导叶及固定导叶区域的损失；二是PT与FT方法进出口条件均为由全通道计算结果提取出来的变量边界条件（profile boundary），计算条件的设置可以认为与全通道相同，而这 2种方法均为非全通道计算，活动导叶及转轮区域固壁面的水力损失均小于全通道方法，故其计算效率偏差略大。

表1 试验与3种不同数值方法的水力效率统计结果Table 1 Statistics results of test hydraulic efficiency and numerical hydraulic efficiency with three different simulation methods

3.2 压力及速度分布

为进一步验证数值模拟的可靠性，本文对比了由活动导叶与转轮之间无叶区至尾水管内各监测点上的平均压力的计算值和试验值，如图6所示。BEP工况下，不同位置测点平均压力数值解和实测值的差异较小，在无叶区和转轮叶片上，平均压力的数值解均高于实测值。对全通道方法而言，其预测的尾水管中平均压力的计算值小于实测值。全通道计算方法、FT及PT方法捕捉的压力均值仅仅在无叶区有较小区别，而转轮叶片上的数值差异几乎可以完全忽略，表明3种计算方法在预测计算域内平均压力上效果相当，且与实测值以及Trivedi等[22,25,28-29]的结果比较一致。

图6所示分别为采用PT方法、FT方法以及全通道方法计算的 0.5倍叶片高度活动导叶与转轮流道内局部静压分布（图 7左侧）、转轮区域内速度云图及速度矢量分布（图 7右侧）。由静压分布可以清楚地看到，由活动导叶进口至转轮出口，压力值均匀减小，未出现突变，表明做功良好。PT法与全通道计算在静止域与旋转域内的压力显示几乎一致，而FT法与其余两种方法在活动导叶进口的静压分布上有区别，主要表现在两方面，一是活动导叶头部对压力分布的影响，二是总体压力值偏低。3种计算方法速度矢量分布比较一致，转轮流道内流线顺畅，未出现漩涡及回流等现象，表明能量转率效率较高。相对于PT方法及全通道计算，FT方法提取的速度矢量在长叶片进口侧压力面上轻微冲击壁面，分析认为FT方法出现不同于其余2种方法是由于其所采用的相变条件向上游的反馈所致。

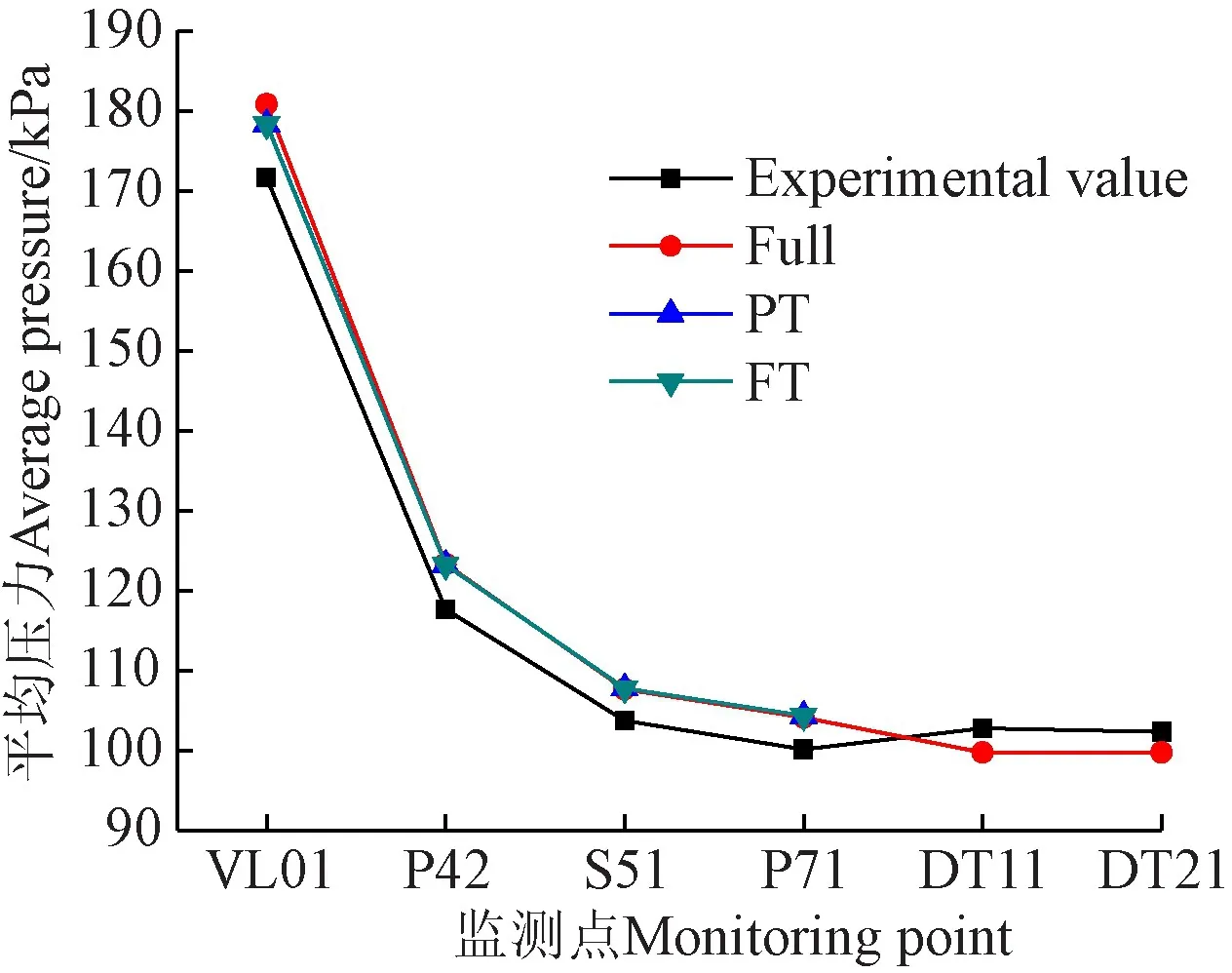
图6 试验与3种计算方法平均压力比较Fig.6 Average pressure comparison of experimental test and numerical simulation with three simulation methods

图7 三种不同模拟方法流道压力及速度分布Fig.7 Pressure and velocity distribution at mid-span plane by three simulation methods

为定量分析流道内压力分布情况，图 8显示了叶片上压力负荷沿弦长的分布。

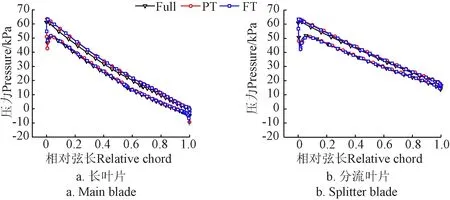
图8 转轮叶片负荷分布Fig.8 Blade load distribution for runner

由图8可知，单通道的PT方法以及双通道的FT方法模拟结果相当，且均获得了与全通道结果比较一致的负荷分布，在相对弦长小于0.8时，PT与FT方法在叶片压力面上的负荷大于全通道方法，其余位置则吻合的较好。结果分析表明，PT与FT方法均可较准确捕捉叶片表面负荷分布。

3.3 叶片合力及扭矩分布

水力效率及不同位置监测点压力均值，均为采用时均法获得，其对外特性及时均流动特性的捕捉比较准确，但水轮机内部流动特征具有强烈的非稳态性，因此应进行时变量的深入分析。图 9所示为一组长短叶片所受合力及扭矩随时间变化规律。由时变叶片受力及扭矩可知，FT与PT法预测结果均小于全通道计算，然而FT方法与全通道比较接近，在幅值的一侧与全通道计算有差别，而另一侧则吻合地较好，且波峰及波谷出现时间间隔相同，仅仅存在一定的相位差，PT方法仅仅捕捉到较小波动且其最大最小值时间间隔与全通道有差别。可以断定，利用采样方法及相变边界条件的FT法能较好地还原时变信号，而PT方法误差较大。

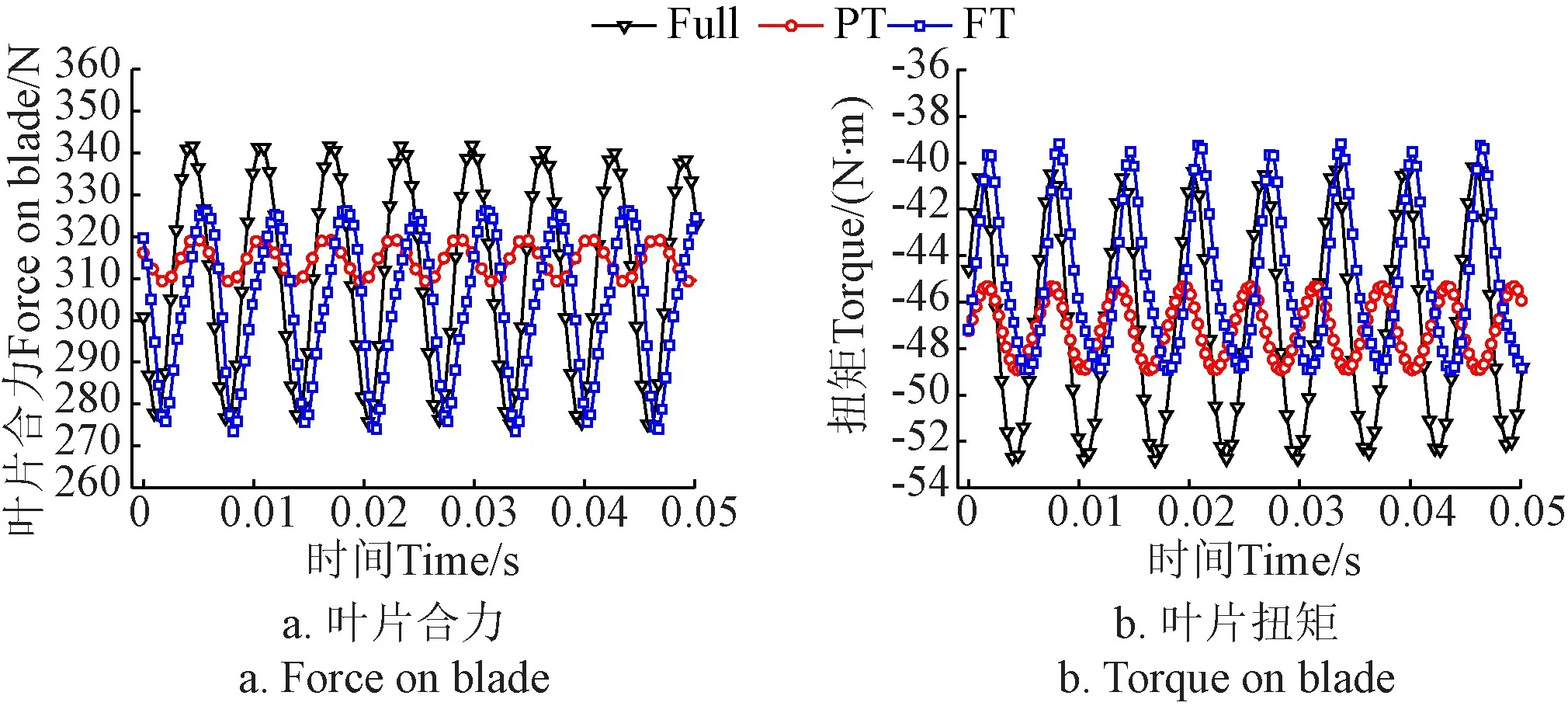
图9 叶片合力及扭矩随时间变化规律Fig.9 Temporal variation of force and torque on blade

3.4 压力脉动频谱特性

本文进一步对数值计算及模型试验各监测点瞬时压力数据进行快速傅里叶变换（FFT），获得各个测点的频谱特性。

模型试验获得的时变压力信息中混掺着电网频率及其谐波，往往在频率中占据主导作用，对原始信号有较强的干扰作用。因此，在进行试验压力脉动及其频谱分析时，必须进行50 Hz及其谐波的滤波处理以消除电网频率的影响。本文采用Matlab对试验原始信号进行滤波处理。图10为试验条件下、BEP工况滤波前后传感器P42频谱图。由图10可知，传感器采集的原始信号的幅值在100，200及300 Hz明显高于其他频率，采用滤波器对信号进行去噪处理，有效去除了电网频率的干扰。

图10 测点P42滤波前后频谱分析对比Fig.10 Spectral analysis of P42 before and after filtering

图11 所示为BEP工况下全通道计算、PT方法、FT方法以及试验结果计算的不同监测位置的压力脉动频谱图，为时变压力数据经过快速傅里叶变换（FTT）而来。图11中，横轴坐标为经过归一化处理的无量纲量，为实际频率与对应工况下转频的比值，即转频的倍数，纵坐标为压力脉动幅值。

图11 压力脉动频谱结果显示，FT方法几乎再现了全通道方法的所有特征，2种不同的数值方案均准确捕捉到了静止域与旋转域测点的主频，即VL01主频为30fn（fn为转频），P42、S51、P71主频为28fn，而PT方法预测的所有主频均为30fn，表明FT方法较准确地还原了原始信号的求解历史，而PT方法由于采用在交界面上对变量进行比例缩放的策略，从而引起频率变化。此外，FT方法与全通道算的明显区别是各个测点上均出现了谐波分量，这是由于信号重构采用了傅里叶分解的缘故。幅值方面，FT法与全通道法幅值大小变化趋势一致，即P42压力幅值最大，VL01次之，然后为S51以及P71。PT法同样为P42最大，而S51次之，然后依次为VL01与P71。相对于试验值，FT方法与全通道在VL01上幅值高于试验值，其余测点则与试验值比较一致，而PT方法VL01上与试验值比较吻合，而其余测点均小于试验值。通过与Nicolle等[22]的压力脉动频谱特性结果对比发现，本文所采用的FT方法捕捉到的压力脉动特性在主频及幅值上与试验值及全通道计算均有较好的一致性，应该与计算域的选取以及网格离散有关。综合对比分析表明，FT方法可以以较少的计算资源捕捉到与全通道相当的RSI效应。