小型农用履带底盘多体动力学建模及验证

刘 妤，张 拓，谢 铌，梁举科

（重庆理工大学机械工程学院，重庆 400054）

0 引 言

丘陵山区农业经济发展潜力巨大[1-2]，但是，其田间地块零碎的特殊地貌导致大中型农业机械无法进场作业，因此，小型山地农业机械需求旺盛[3-4]。履带底盘具有接地比压小、转向灵活、机动性好等优异性能，不失为小型山地农业机械动力底盘的一种优选方案[5]。

近年来，虚拟样机技术发展迅速[6-10]。Franceso Mocera等[11]利用动力学软件建立了农用履带车辆的多体动力学模型，研究了模型的惯性参数，分析了驱动轮转速对履带车辆运动规律的影响，并评价了理论车速与实际车速之间的差异； Chen等[12]建立了履带战车的刚柔耦合模型，并对履带底盘的关键部件进行了疲劳分析和寿命计算；Ottonello等[13]通过多体仿真，讨论了不同驱动方式对无人驾驶履带车辆 Elloboat的影响；孙强等[14]利用MatlabSimulink对Cruise进行了二次开发，实现了履带式推土机的快速建模。王川伟等[15]设计了一种四摆臂-六履带机器人，并利用Adams建立了机器人虚拟样机模型，并在虚拟环境下完成了单侧双重障碍地形越障仿真试验；梁梓等[16]基于动力学仿真研究了轻型履带车辆载荷谱编制的新方法。可见，多体动力学建模及仿真已经成为研究履带车辆动力学性能的重要手段[17-19]，但是，现有的文献报道多局限在履带车辆的建模及仿真，模型的有效性、可信度有待考证，涉及实车试验验证模型的研究甚少。

本文以自主研制的小型农用履带底盘为对象，拟建立履带底盘的多体动力学模型，并通过实车试验与仿真结果的对比验证模型的有效性、可信度。

1 履带底盘动力学模型的建立

结合小型山地农业机械的作业环境，确定小型农用履带底盘的主要技术指标为：1）整机空载质量≤300 kg，满载质量≤400 kg；2）正常行驶速度范围为2～4 km/h；3）在松软路面稳具备较好的路面通过能力，满载接地比压＜30 kPa；4）具备较好的爬坡越障能力，最大爬坡角度≥20°，可跨越壕沟宽度≥0.5 m；5）操纵方式简单且能灵活转向，具有较小的转向半径。按照模块化理念所设计的履带底盘结构如图1所示，整体尺寸1 520 mm×1 000 mm×480 mm，主要由车体、行走系统、动力系统和控制系统等模块组成。其中，行走系统采用了传统的倒梯形布局，主要包括驱动轮、诱导轮、拖带轮、支重轮、张紧装置和游离三角等部件，支重轮按照平衡悬架的结构布置，通过游离三角与车架铰接，其优点在于支重轮的位置可以根据地形被动调节，避免了支重轮悬空而导致载荷分布不均匀[20]，从而提高履带底盘的操纵稳定性。而在驱动方式上，该履带底盘突破了传统的转向方式，采用双电机分别驱动两侧的行走系统，通过控制两侧电机的不同转速以实现不同半径的转向，从而提高履带底盘运动的灵活性。

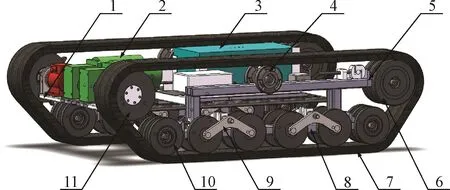
图1 小型履带底盘结构示意图Fig.1 Structure diagram of small crawler chassis

1.1 履带底盘运动学方程

假定路面为硬质路面，不考虑土壤的剪切变形，路面不平度不会因底盘碾压而发生变化。为分析履带底盘平面内的运动学关系，视履带底盘由车体（含其上所搭载的相关部件）和左、右侧履带系统所组成，其平面运动学关系如图2所示。为简化推导，作如下假设：1）车体与行走系统无相对运动；2）只考虑履带底盘的垂直运动和俯仰运动，不考虑横向滑移运动；3）履带长度在底盘行驶过程中不会发生变化，且履带与轮系部件之间无相对滑移。

设惯性坐标系为O-XY，履带底盘的运动方程由履带底盘质心Om(xm,ym)和方向角mφ决定。结合图2所示的几何关系，分析i和i+1时刻，可得

取履带底盘的广义坐标为[21-22]

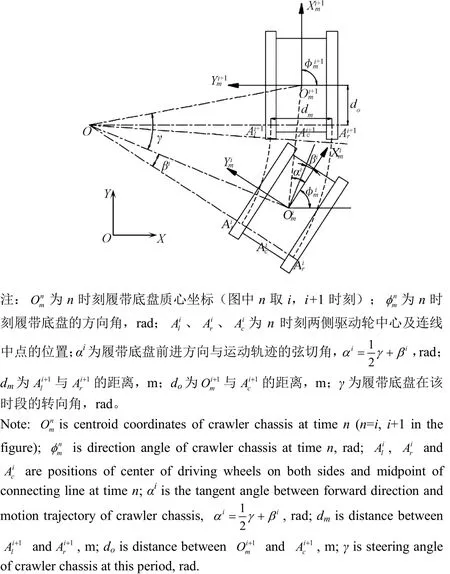
图2 小型农用履带底盘平面运动学关系Fig.2 Plane kinematics diagram of small agricultural crawler chassis

运用极限理论和瞬态运动分析法[23-24]所建立的履带底盘运动学方程为

式中r为驱动轮半径，m；lq˙、rq˙分别为左、右两侧驱动轮转角，rad；lxs˙、rxs˙为左、右两侧履带纵向滑动位移，m；v为广义速度。

对式（5）求导，则

由此可得履带底盘行驶过程中的速度、加速度、角速度、角加速度等运动特性参数。

1.2 履带底盘动力学方程

履带底盘的动势L为

式中K为履带底盘的动能，J；P为履带底盘的势能，J。若以地面为零势能面，则

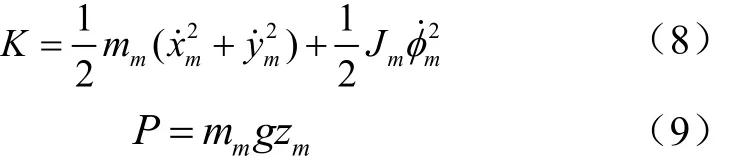
式中mm为履带底盘的总质量，kg；(xm,ym,zm)为履带底盘质心的坐标；Jm为履带底盘的转动惯量，kg·m2。

履带底盘的动能K也可以用矩阵形式表示，即

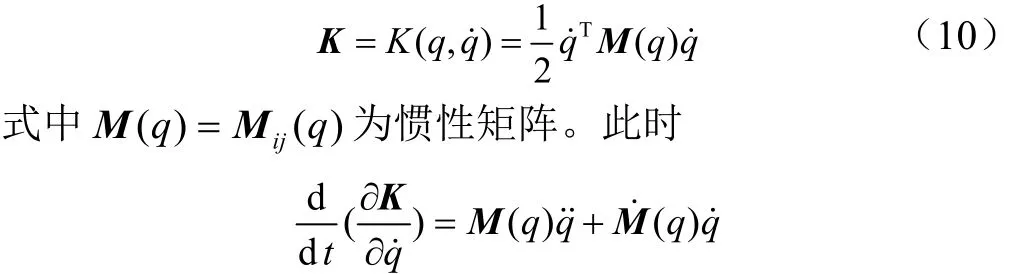
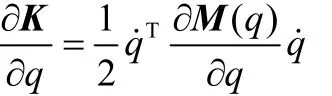
而

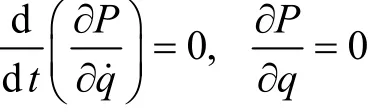
所以，履带底盘的拉格朗日动力学方程为[25]

式中F是与非有势力相对应的广义力。

1.3 履带底盘拓扑结构分析

对履带底盘进行建模时，在确保各部件运动关系与实际情况相符的前提下，需对底盘行走系统各部件做相应简化。其中，游离三角与车体采用旋转副进行约束，张紧装置与车体采用平移副和阻尼弹簧进行约束，各轮系部件与其对应的联接部件采用旋转副进行约束，以确保行走部分各部件具有确定的运动关系。同时，为提高模型解算速度及计算效率，将履带底盘的其余部件与车体合并为一个刚体系统模型[26]。

根据简化后各部件之间的约束关系，建立履带底盘模型的拓扑结构如图3所示，各部件及约束如表1所示。

图3 小型农用履带底盘模型的拓扑结构Fig.3 Topology structure of small agricultural crawler chassis

表1 小型履带底盘各部件之间的约束情况Table 1 Constraints between components of small crawler chassis

1.4 履带底盘多体动力学模型

分析前述所建立的履带底盘运动学方程和动力学方程，可见影响其动力学性能的主要包括质量、质心位置、转动惯量、惯性矩等质量特性参数。鉴于理论解算的复杂性，因此，本文考虑基于以上数学模型建立履带底盘的多体动力学模型。

首先，借助三维软件 SolidWorks，建立履带底盘各部件的三维模型，并计算质量特性；其次，将履带底盘车体部分的三维模型导入多体动力学软件RecurDyn，在RecurDyn/Track（LM）环境中对履带、驱动轮、张紧轮及其他轮系部件进行参数化建模，并完成装配，建立初步的履带底盘多体动力学模型；再者，结合履带底盘的拓扑结构分析，定义模型各部件之间的约束关系，并根据前述计算结果定义各部件的质量特性参数；最后，根据履带底盘空转工况下实车试验结果，利用试凑法[27]对履带内部衬套力的刚度系数、阻尼系数以及部件的摩擦系数进行调试，再结合所采集的履带底盘样机静止状态下的履带张紧力定义模型中履带的预张紧力，进而完成履带底盘的多体动力学建模。所建立的履带底盘多体动力学模型如图4所示。

图4 小型农用履带底盘多体动力学模型Fig.4 Multi-body dynamic model of small agricultural crawler chassis

2 模型验证

单纯从理论角度验证多体动力学模型是否有效是十分困难的。鉴于小型农用机械的作业环境既包括耕地路面，也包括转场作业的水泥路面，因此，本文通过硬质、松软 2种路面环境下履带底盘直线行驶的实车试验与仿真结果的对比分析验证模型的有效性、可信度。考虑到履带车辆的行驶速度、驱动转矩和履带张紧力是评价其动力学性能的主要参考依据[21]，而侧向偏移量直接影响履带车辆的行驶稳定性，因此，在下述模型验证中，重点关注的参数包括履带底盘行驶过程中的平均速度、侧向偏移量、驱动轮转矩和履带张紧力。

2.1 实车试验条件

硬质路面行驶试验在校内一段水泥平直路面进行，该路段长50 m；松软路面行驶试验在校内一块翻整后的试验田中进行（试验当天测试得土壤含水率24.3%、土壤坚实度6.2 kg/m2），该路段长40 m且路面表面无明显障碍物，分别测试履带底盘在2种路面下的直线行驶性能。数据采集系统如图 5所示，传感器均选用金诺传感器有限公司的产品，其中，JN-DN型动态扭矩传感器用于采集履带底盘行驶过程中的驱动轮转速和转矩，该传感器精度为0.5%，采样频率10 Hz；JBHS-2000kg型拉压力传感器用于采集履带张紧力的变化，该传感器精度为0.1%，采样频率10 Hz。测试中，传感器通过无线发射模块将所采集的数据传输至PC机，通过上位机程序进行处理、储存并显示。

图5 履带底盘数据采集系统Fig.5 Data collection system of crawler chassis

2.2 仿真分析条件

通过实车试验获取的履带底盘在硬质路面和松软路面 2种环境下行驶时驱动轮的平均转速分别为 94和82 r/min，所以仿真分析中利用驱动函数STEP模拟履带底盘由启动到匀速行驶的过程。同时，结合传感器的采样频率，仿真步长设置为0.1 s。

2.2.1 路面参数设置

结合实车试验环境参数，利用动力学软件重构仿真地面。仿真地面的特征参数如表 2所示，其中，水泥路面为硬质路面，不会因履带的碾压而产生形变，所以分析中履带板与地面的接触采用接触碰撞摩擦模型来模拟[28]；耕地路面土质松软，履带碾压会引起土壤形变，因此分析中需要考虑土壤的剪切变形，利用贝克的压力—沉陷关系模型进行模拟[8]，结合试验场地的土壤特性，仿真路面设置为黏土环境。

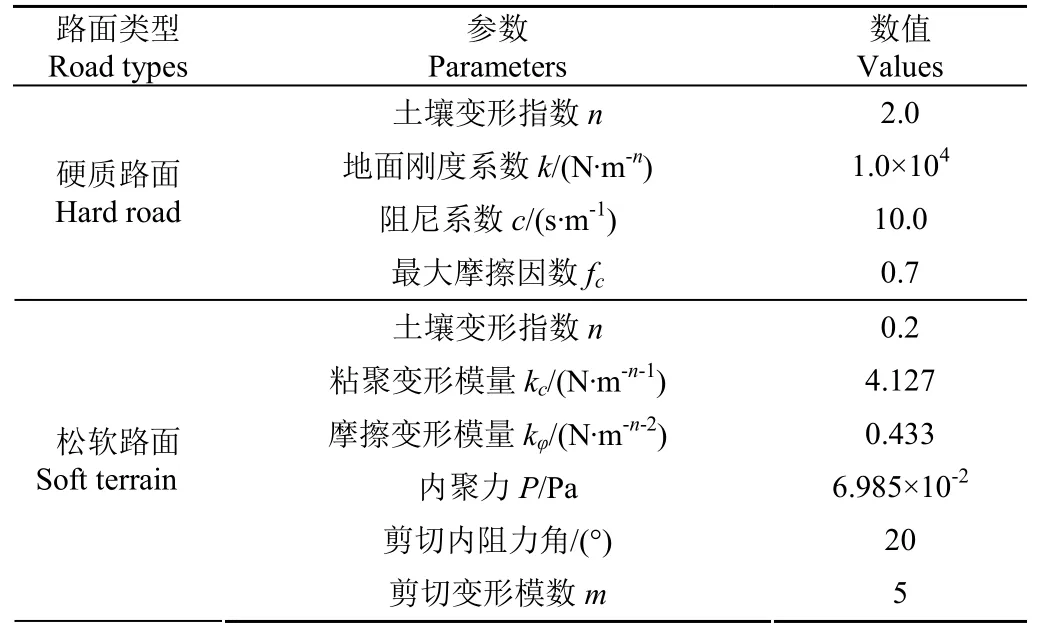
表2 仿真路面特征参数Table 2 Characteristic parameters of simulation pavement

2.2.2 二维随机路面建立

根据文献[29]，平直水泥路面归于B级路面，耕地归于 E级路面。根据文献[30]，利用谐波叠加法在 Matlab中对试验路面不平度进行了重构，重构路面不平度曲线如图6所示。

2.3 模型验证

2.3.1 硬质路面直线行驶工况

实车试验中，履带底盘样机每次均以相同的速度匀速通过长50 m的测试路段并记录通过该路段所需要的时间，4次重复试验所测得的通过时间分别为41.8、41.3、41.7、41.6 s，由此可得履带底盘的平均行驶速度为1.20 m/s。仿真分析中，基于图4模型的行驶速度仿真曲线如图7所示，可见，平均速度为1.14 m/s，略低于实测速度，相对误差为5.00%。

图7 小型履带底盘在硬质路面上直线行驶速度仿真曲线Fig.7 Simulation curve of straight running speed of small crawler chassis on hard road

上述 4次实车试验中所测得的履带底盘侧向偏移量分别为0.685、0.730、0.711、0.670 m，由此可得履带底盘的平均侧向偏移量为0.699 m。而仿真分析所得到的模型行驶轨迹曲线如图 8所示，可见，履带底盘在终点处的累计跑偏量为0.672 m，略低于实车试验的平均侧向偏移量，相对误差为3.86%。

图8 小型履带底盘在硬质路面上侧向偏移量仿真曲线Fig.8 Simulation curve of side position offset of small crawler chassis on hard road

履带底盘直线行驶工况下驱动轮转矩的实测数据与仿真结果的对比如图9a所示。可见，试验测得的驱动轮转矩均值为 27.65 N·m，仿真分析所得到的均值为26.78 N·m，相对误差为 3.15%；实测曲线和仿真曲线的极差分别为29.5、28.6 N·m，相对误差3.05%。均值及极差分析结果表明，驱动轮转矩的实测曲线与仿真曲线的峰值相差较小。进一步，利用变异系数（CV）评价曲线的变异程度（波动）。记s为样本的标准差，x为样本的平均值，则

数据处理后得到的实测曲线和仿真曲线的标准差分别为5.28、4.59 N·m，所以，二者的变异系数分别为19.10%和17.14%，可见，实测曲线和仿真曲线的波动程度比较接近。

图9 小型农用履带底盘在硬质路面行驶时关键参数对比Fig.9 Comparison of key parameters of small agricultural crawler chassis on hard road

履带底盘直线行驶工况下履带张紧力的实测数据与仿真结果的对比如图9b所示。可见，实测张紧力均值为2 988.45 N，仿真分析所得到的均值为2 992.95 N，相对误差仅为0.15%；同时，实测曲线和仿真曲线的极差分别为303.8、295.3 N，相对误差为2.80%，所以，二者在峰值上具有较好的一致性。数据处理后得到实测曲线和仿真曲线的标准差分别为61.16、55.67 N，二者的变异系数分别为2.05%、1.86%，可见，实测曲线和仿真曲线的波动程度也比较接近。

2.3.2 松软路面直线行驶工况

同理，进行履带底盘松软路面直线行驶工况下的实车试验与仿真分析。实车试验中，履带底盘样机每次均以相同的速度匀速通过长40 m的测试路段，4次重复试验所测得的履带底盘的平均行驶速度、平均侧向偏移量分别为0.925 m/s，0.776 m，而仿真分析所得到的行驶速度仿真曲线、模型行驶轨迹曲线分别如图10、图11所示，可见，履带底盘的平均速度为0.946 m/s，在终点处的累计跑偏量为0.723 m，与实测值的相对误差分别为2.27%、6.83%。

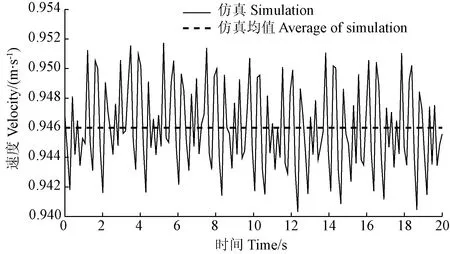
图10 小型履带底盘在松软路面上直线行驶速度仿真曲线Fig.10 Simulation curve of straight running speed of small crawler chassis on soft terrain

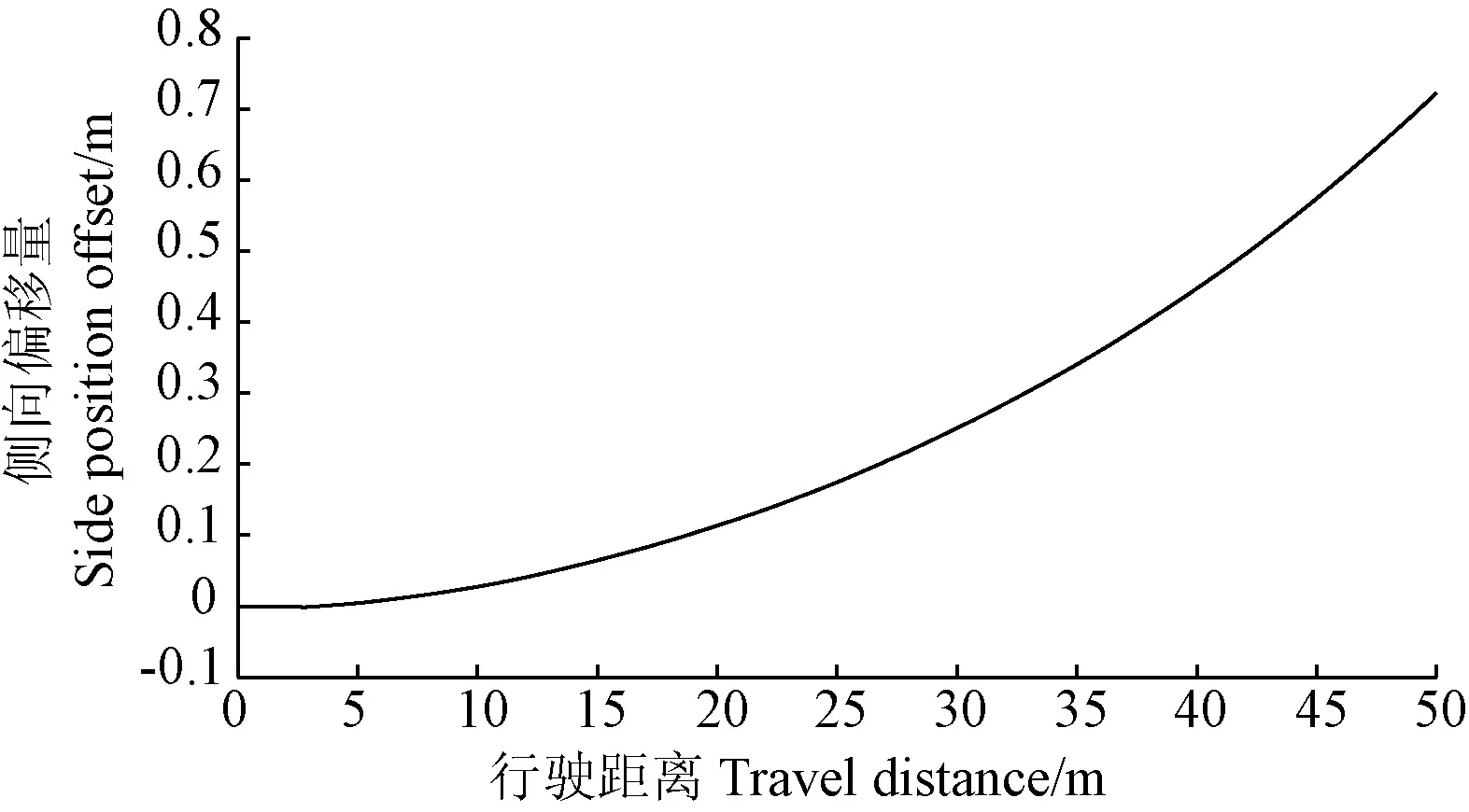
图11 小型履带底盘在松软路面上侧向偏移量仿真曲线Fig.11 Simulation curve of side position offset of small crawler chassis on soft terrain

履带底盘直线行驶工况下驱动轮转矩、张紧力的实测数据与仿真结果的对比如图 12所示。由此可得：1）对于驱动轮转矩（图12a），实测均值、仿真均值分别为37.539、35.79 N·m，相对误差4.66%；实测曲线和仿真曲线的极差分别为54.8、50.8 N·m，相对误差7.3%；2条曲线的变异系数分别为26.53%、24.47%，波动程度比较接近。2）对于履带张紧力（图 12b），实测均值、仿真均值分别为2 817.69、2 835.23 N，相对误差0.62%；实测曲线和仿真曲线的极差分别为646.8、620.79 N，相对误差4.02%，二者在峰值上具有较好的一致性；实测曲线和仿真曲线的变异系数分别为4.32%和4.84%，波动程度也比较接近。

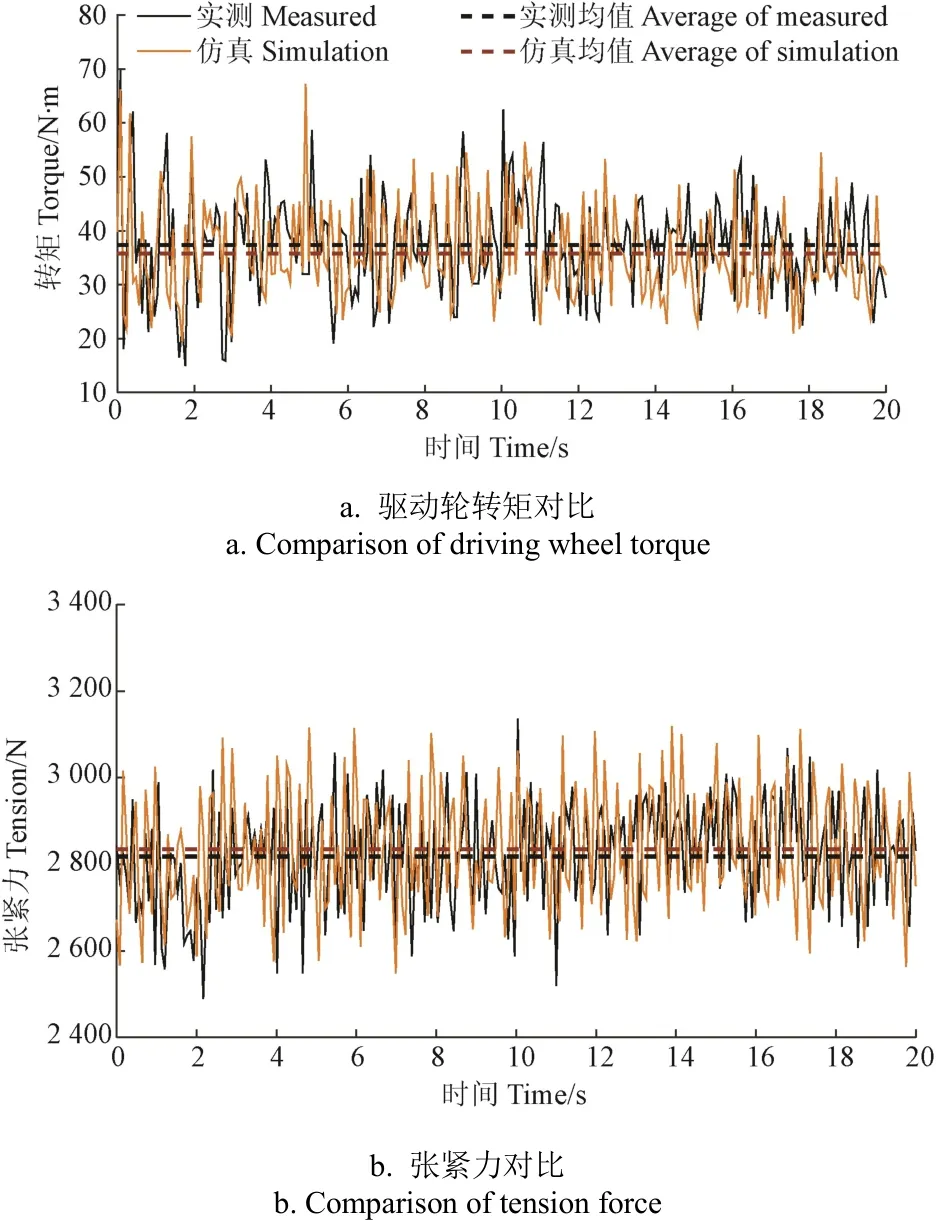
图12 小型农用履带在底盘松软路面行驶时关键参数对比Fig.12 Comparison of key parameters of small agricultural crawler chassis on soft terrain

综合分析，通过对比履带底盘在硬质路面和松软路面行驶时平均速度、侧向偏移量、驱动轮转矩和履带张紧力等实车试验数据和仿真分析数据，可以发现两种工况下数据吻合度均较好，这表明所建立的履带底盘动力学模型是有效的、可信的，能够较客观地反映履带底盘行驶过程中的动力学性能。

进一步分析引起误差的原因，主要在于：1）履带底盘建模过程中对部分结构进行了简化，而实车试验用样机会受加工误差、装配误差的影响，因此，仿真模型与实际样机不可避免地存在一定的差异；2）实车试验路面与仿真路面有所区别，相对仿真路面平整度较低，导致底盘行走过程中因受力不稳定而产生波动，进而导致实车试验结果相较仿真结果波动偏大。

3 结 论

本文以自主研制的小型农用履带底盘为对象，建立了履带底盘的多体动力学模型，并对其有效性、可信度进行了试验验证。实车试验与仿真结果的对比分析结果表明：履带底盘在硬质路面和松软路面 2种环境下直线行驶时，平均行驶速度、侧向偏移量、驱动轮转矩和履带张紧力等参数的相对误差分别为5.00%、2.27%，3.86%、6.83%，3.15%、4.66%，0.15%、0.62%，吻合度较好，说明所建立的履带底盘动力学模型是有效的、可信的，后期可借助该模型进一步深入研究履带底盘的行驶特性。