光滑双向渐进结构优化法拓扑优化连续体结构频率和动刚度

滕晓艳，毛炳坤，江旭东

（1. 哈尔滨工程大学机电工程学院，哈尔滨 150001；2. 哈尔滨理工大学机械动力工程学院，哈尔滨 150080）

0 引 言

结构拓扑优化设计通过寻求在满足性能最优条件下，结构材料在设计空间中沿最佳传力路径布局的拓扑形式。近三十年来，形成了许多基于梯度或启发式的拓扑优化方法，主要包括变密度法、均匀化法、变边界法（水平集法和相场法）以及渐进结构优化方法（evolutionary structural optimization, ESO）等[1-3]。

ESO法最初由Xie和Steven提出，基于生物进化思想，利用单元灵敏度信息逐渐删除低效单元，从而得到优化的拓扑结构[4]。双向渐进结构优化方法（bi-directional evolutionary structural optimization, BESO）继承了ESO法的进化思想，不但可以删除结构的低效单元，还可以在结构中需要的部位添加高效单元，BESO方法在结构应力、静刚度、频率、屈曲以及依附性载荷问题方面得到了广泛的应用[5]。但是，Zhou等[6]指出ESO法的进化准则导致方法存在单元过删除问题，通过端部弹性支撑的悬臂梁结构的优化问题的求解失效验证了方法存在的理论缺陷。尽管Huang等[7]通过细密网格和设置较低进化率解决了上述测试模型的优化问题，但是由此也表明 ESO法或 BESO法的进化准则存在网格的强依赖性问题，可能导致优化失败或非最优解。贺丹等[8]认为单元相对密度较大的进化步长可能引起较大的灵敏度误差，导致进化准则的失效。匡兵等[9]根据灵敏度信息评价单元对结构性能的影响，建立单元相对密度进化步长的控制模型以调谐单元的删除率和添加率，以避免由于误删单元导致优化失败。Valerio等[10-12]提出了一种基于软杀策略的光滑渐进结构优化（smooth evolutionary structural optimization,SESO）方法，根据单元对结构性能的贡献调整单元刚度，控制低效单元在结构进化过程中逐渐被删除，有效解决了结构的强度、静刚度以及多约束优化问题。

结构动力学拓扑优化包括 2类设计问题：结构动力特性（固有频率）优化和结构动力响应（振动激励下结构的位移、速度、加速度、应力和应变能等）优化。动力特性拓扑优化主要是通过提高结构的低阶固有频率来避开外部激励频率，其最终目的仍然是为了实现结构动力响应优化。结构动力学优化涉及灵敏度计算、动响应分析以及约束函数处理等方面的问题，优化算法需要反复计算结构响应对设计变量的偏导数，对于大规模与多变量结构的动力学优化问题，所消耗的计算资源往往是难以承受的[13-16]。为了有效减小结构动力学优化过程的求解规模，Park等[17]提出等效静载荷法（equivalent static loads, ESL）将动力学优化问题转化为静力学多工况优化问题，利用结构线性优化技术求解动态线性优化问题。Stolpe[18]通过数学规划法证明了ESL法满足KKT优化准则，从数学上验证了优化方法的有效性。Jang等[19]基于ESL法，以降低结构峰值响应为目标，研究了不同载荷特征以及动态多工况问题的动力学拓扑优化方法。Kim等[20-21]为了缩减结构动力学优化规模，将自由度缩聚方法或模型降阶技术与结构线性静态优化技术相融合，研究了基于系统缩减方法的ESL动力响应优化问题。陈涛等[22-23]针对ESL法求解结构动态非线性优化问题收敛效率低的问题，结合静态线性优化方法与最速下降法提出了ESL梯度优化方法，解决了汽车正面碰撞关键结构优化设计问题。高云凯等[24-26]将ESL与变密度法相融合，求解了结构非线性动力学拓扑优化问题；但是，低密度单元的局部伪模态和网格畸变使优化过程难于收敛。

综上，SESO的光滑渐进优化策略能够有效抑制低效单元的过删除问题，同时采用的软杀策略亦可避免低密度单元的局部伪模态和网格畸变等奇异性问题。由此，本文以SESO静力学拓扑优化为基础，提出光滑双向渐进结构优化方法（smooth bi-directional evolutionary structural optimization, SBESO），求解连续结构的频率和动刚度动力学拓扑优化问题。以结构固有频率最大化为目标，构建基于SBESO法的频率优化模型。研究SBESO算法参数对收敛性及优化解的影响。以结构动刚度最大化为目标，融合等效静载荷法（ESL）与光滑双向渐进结构优化方法（SBESO），提出动载荷作用下的结构动刚度优化方法。

1 光滑双向渐进结构优化方法

基于渐进结构优化方法，结构动力学拓扑优化的数学模型表述如下

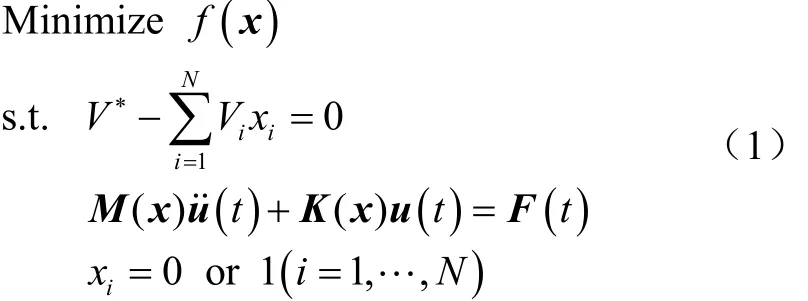
对于传统的BESO方法，通过式(1)的梯度信息评价添加/删除单元对目标函数变化量的影响，根据滤波后的灵敏度信息和体积约束确定当前设计域中同时添加的单元集和删除的单元集，相应的渐进优化准则为

传统 BESO方法中，较大的单元相对密度的进化步长，导致利用目标函数梯度信息确定结构低效单元可能引起较大的系统误差，引起非低效单元的误删除问题，最终将造成优化失败或得不到最优解。由此，将式(2)中的单元灵敏度按升序排列，中删除率q的单元集将被删除，中1-q的单元集将返回设计域。此外，ΓGS中的单元特性-质量矩阵和刚度矩阵通过权重函数更新返回设计域（如图 1 所示）。光滑双向渐进结构优化准则及流程图见图1和图2。上述方法即为光滑双向渐进结构优化（smooth bi-directional evolutionary structural optimization, SBESO）方法，相应的光滑渐进优化准则为

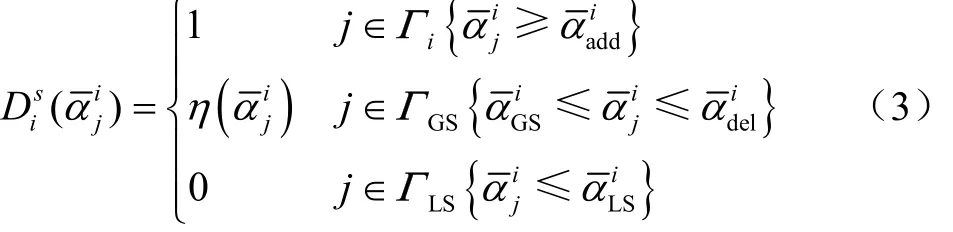
图1 光滑双向渐进结构优化法的渐进优化准则Fig.1 Evolutionary optimization criterion of smooth bi-directional evolutionary structural optimization method

对于SBESO方法，根据式（3），结构在第i次优化迭代中设计域中单元j的质量与刚度矩阵分别为

由式（4）与式（5）可以看出，权重函数根据单元对结构性能的贡献调节单元质量与刚度矩阵，能够保证低效单元的质量与刚度在优化迭代中逐渐趋向于0，进而从结构设计域中渐进删除。因此，SBESO方法通过引进权重函数和控制单元删除率可以有效抑制单元过删除问题，提高渐进优化方法的寻优能力。

图2 SBESO方法优化流程Fig.2 Optimal procedure of SBESO

根据 SBESO法的渐进优化准则，如果删除率q=100%，则SBESO方法退化为传统的BESO方法，由此式（4）、式（5）退化为

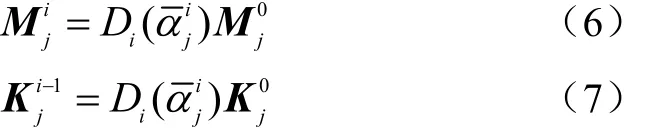
基于经典有限元理论，结构动力学控制方程为

将式（6）与式（7）代入式（8）中，得到优化结构当前设计域的动力学控制方程为

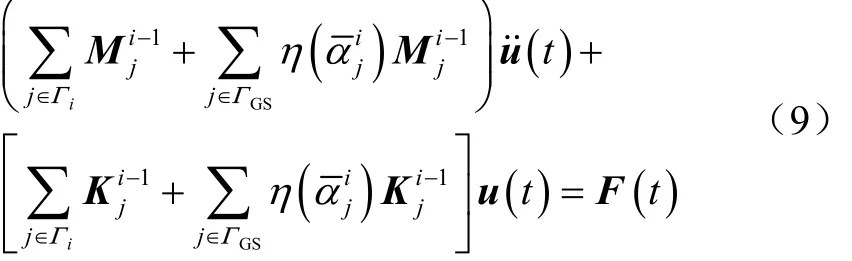
结构进化过程中在达到体积约束后，目标函数仍需满足如下收敛准则

式中 error为综合目标函数的误差，k为当前迭代数，ε1为收敛容差，N′为整数，在第迭代步的值。图2阐明了基于光滑双向渐进结构优化方法的优化流程。

由图2可知，则SBESO优化步骤如下所述：1）设置SBESO的删除率q、进化率ER、目标体积V*、单元灵敏度过滤半径 rmin、权重函数等算法参数，利用有限元网格离散初始设计域；2）定义位移边界约束条件和载荷，对结构进行有限元分析，计算所有单元的灵敏度；3）按照灵敏度的大小设置阀值，按照阀值把所有单元划分为3个区域Γi，ΓGS，ΓLS；4）向当前设计域中添加Γi区域中的单元，完全移除ΓLS区域中的单元，按照权重函数η（）修改Γ 区域内的单元质量与刚度矩阵；5）重复GS步骤 2）～4），直至在结构同时达到目标体积和满足收敛准则时终止优化过程。

2 频率优化

2.1 数学模型

以结构l阶固有频率最大为目标，则基于SBESO方法的结构频率优化模型表述为

式中ωl为结构l阶固有频率，φl为结构l阶归一化振型。

对于无阻尼振动系统，优化结构的固有频率可表示为Rayleigh商形式，则有

通过式（12）计算目标频率对设计变量的偏导数，得到单元的灵敏度，表示为

由此，联立式（13）、式（4）和式（5），解算结构频率灵敏度。结合频率梯度信息，根据单元进化准则，对低效单元进行删除。

2.2 数值算例

以两端简支薄板结构的一阶固有频率最大化为优化目标，目标体积为总体积的 50%。薄板结构初始设计域的几何尺寸为240 mm×30 mm（如图3所示），材料的杨氏模量为 E=10 GPa，泊松比为 μ=0.3，材料的密度ρ=1×103kg/m3。利用 4节点双线性平面应力单元将结构设计域划分为240×30个单元，采用的权重函数为线性函数，SBESO算法参数为：删除率q=40%～100%，ε1=0.02，灵敏度过滤半径rmin=5 mm，惩罚因子p=3。

图3 两端简支薄板结构示意图Fig.3 Schematic diagram of plate simply supported along both ends

BESO方法与SBESO方法优化后的频率几乎相等，2种方法的频率值均随迭代过程单调增加（除跃变点外），渐进收敛到最优值（如图4所示）。对于BESO方法，单元过删除（删除率q=100%）引起优化过程中的结构拓扑的不连续，进而形成频率值在迭代过程中跃变为零频率的现象。对于SBESO方法，随着删除率的降低（删除率 q=70%～40%），误删除的低效单元逐渐减少，致使迭代过程中频率值的跃变现象随着单元删除率的减少逐渐得到抑制；同时，结构拓扑优化构形与也随单元删除率的减少逐渐逼近于同一构形。

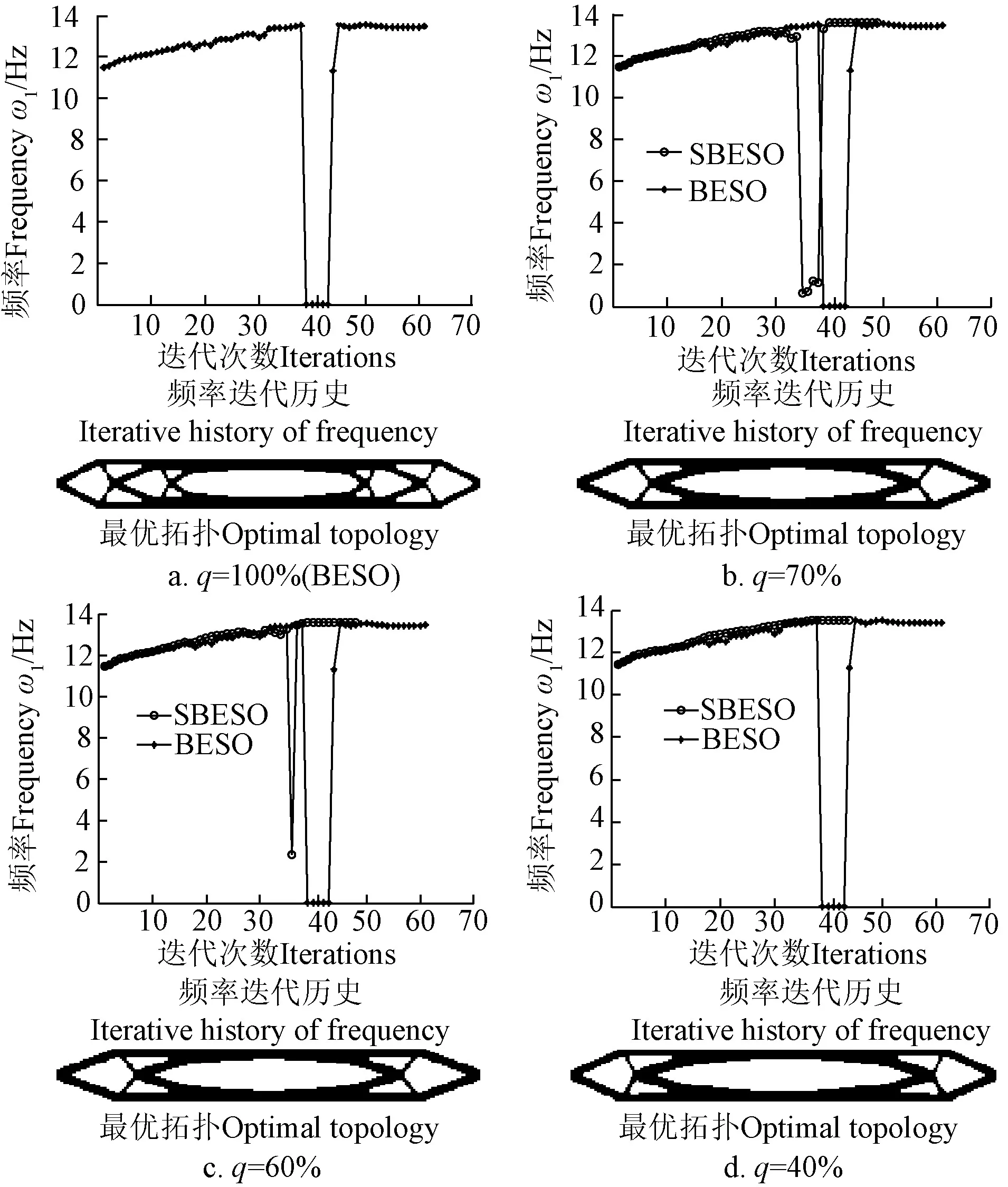
图4 删除率q对频率优化拓扑与收敛过程的影响Fig.4 Effect of deletion rate q on optimal topology of frequency and corresponding process

对比分析权重函数（常函数、线性函数和正弦函）的光滑性对 SBESO结构优化拓扑构形及收敛过程的影响。由于常函数权重函数的光滑性最差，致使单元过删除的抑制效果不显著和频率值跃变现象的存在，SBESO优化拓扑构形（图5b所示）接近于BESO方法的优化结果（图4a所示）。但是，线性和正弦权重函数的光滑性显著增强，有效抑制了单元过删除问题，致使低效单元逐渐被删除和迭代过程更光滑，均收敛于同一最优拓扑结构（图4d和5a所示）。由此，采用线性和正弦权重函数更有利于获得结构最优拓扑解。

图5 不同权重函数对优化拓扑与收敛过程的影响(q=40%)Fig.5 Effect of weight function on optimal topology and corresponding process (q=40%)

3 动刚度优化

3.1 数学模型

动刚度优化作为结构动力响应优化问题，旨在降低结构在振动激励下的应变能来实现结构的动力性能优化。由于结构动柔度（即应变能）是全局刚度的逆测度，因此，动载荷作用下结构动刚度优化数学模型表述如下[25]

式中常数m表示总时间步。对于式(14)表述的大规模的结构动力学拓扑优化问题，传统的基于梯度的优化算法需要反复计算结构动响应和约束函数对设计变量的偏导数，而启发式优化算法不需要目标函数和约束函数的梯度信息，但需要计算函数值，从而不可避免地进行大规模结构分析，上述2种方法使得计算资源的消耗是难以承受的。

等效静载荷法的优化过程由分析域（外层循环）和设计域（内层循环）组成（如图 6所示）。分析域进行结构动态响应分析，得到结构各时间步的位移场；设计域根据位移响应计算等效静载荷，按时间步将等效静载荷处理为多载荷工况，实施线性静态优化，然后更新设计变量返回到设计域重新计算。

图6 等效静载荷法的基本思想Fig.6 Fundamental principle of equivalent static loads method

在内层循环的第一次迭代中，结构初始静态位移场与动态响应分析的位移场是完全相同的。通过式（9），可以确定任一时间步的动态位移场 ()t*u ，则基于位移场等效原理获得等效静载荷eq()t*f

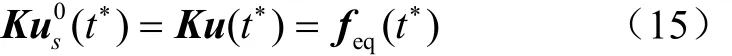
对于无阻尼振动系统，系统的特征方程表示为

尽管式（17）可精确计算结构的等效静载荷，但是，它需要完成模态分析和非常昂贵的瞬态分析以及代数方程组计算。因此，为了减少动响应问题的计算规模，通过一种等效静载荷的近似计算方法，将等效静载荷仅施加于实际动载荷作用的附近区域节点，即假设等效静载荷存在如下l个非零分量，则有

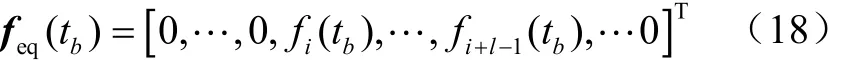
将式（18）代入式（17），则有

因此，基于等效静载荷法，则式(14)描述的结构动刚度优化模型转化为静态线性多工况刚度优化模型，则有

基于SBESO方法，结合静态线性多工况刚度优化模型的灵敏度计算，得到式（20）的灵敏度计算公式，表示为

为了保证单元相对密度在优化过程中的收敛性，定义单元相对密度的收敛准则

结合 ESL方法和 SBESO方法，提出连续体结构动刚度优化算法。主要优化流程如下：1）设置优化算法参数与初始设计变量，定义结构初始设计域的几何形式、外载荷与位移边界条件，建立结构的动态分析有限元模型；2）基于位移场等效原理，利用式（15）解算结构在外部激振力作用下的等效静载荷，按时间步将等效静载荷处理为多工步外载荷，根据式（21）计算单元灵敏度，进行静态线性多工况刚度优化；3）根据静态线性优化结果更新设计变量，按照式（4）和式（5）返回单元质量与刚度矩阵。重复上述步骤，直到最后剩余单元同时满足体积约束以及式（10）和式（22）的收敛准则。

3.2 数值算例

以一端固定薄板结构的动刚度最大化为优化目标，目标体积为总体积的 50%。薄板结构初始设计域的几何尺寸为120 mm×30 mm，右端承受简谐载荷 ()ft~ 的作用（如图7所示）。材料的杨氏模量为E=2 GPa，泊松比为μ=0.3，材料的密度ρ=4.8×103kg/m3。利用4节点双线性平面应力单元将结构设计域划分为120×30个单元，采用的权重函数为线性函数，SBESO算法参数为：删除率q=60%～100%，error=0.02，灵敏度过滤半径rmin=3 mm，惩罚因子p=3。

图7 薄板结构的动刚度拓扑优化Fig.7 Topology optimization of dynamic stiffness of thin plate

BESO方法与SBESO方法优化后的动柔顺度几乎相等，2种方法均渐进收敛到最优值（如图8所示）。

对于BESO方法，单元过删除（删除率q=100%）问题致使部分非低效单元在迭代过程中误删除，并且无法有效控制低效单元在优化过程中逐渐被删除，拓扑构形可能陷入某一低效最优解，优化构形的边界比较粗糙；而对于SBESO方法，能够控制低效单元在优化过程中质量与刚度逐渐趋向于0，进而从设计域中逐渐删除，同时使得迭代过程中结构拓扑优化构形随单元删除率的减少其结构边界逐渐光滑，而且逼近于同一构形。

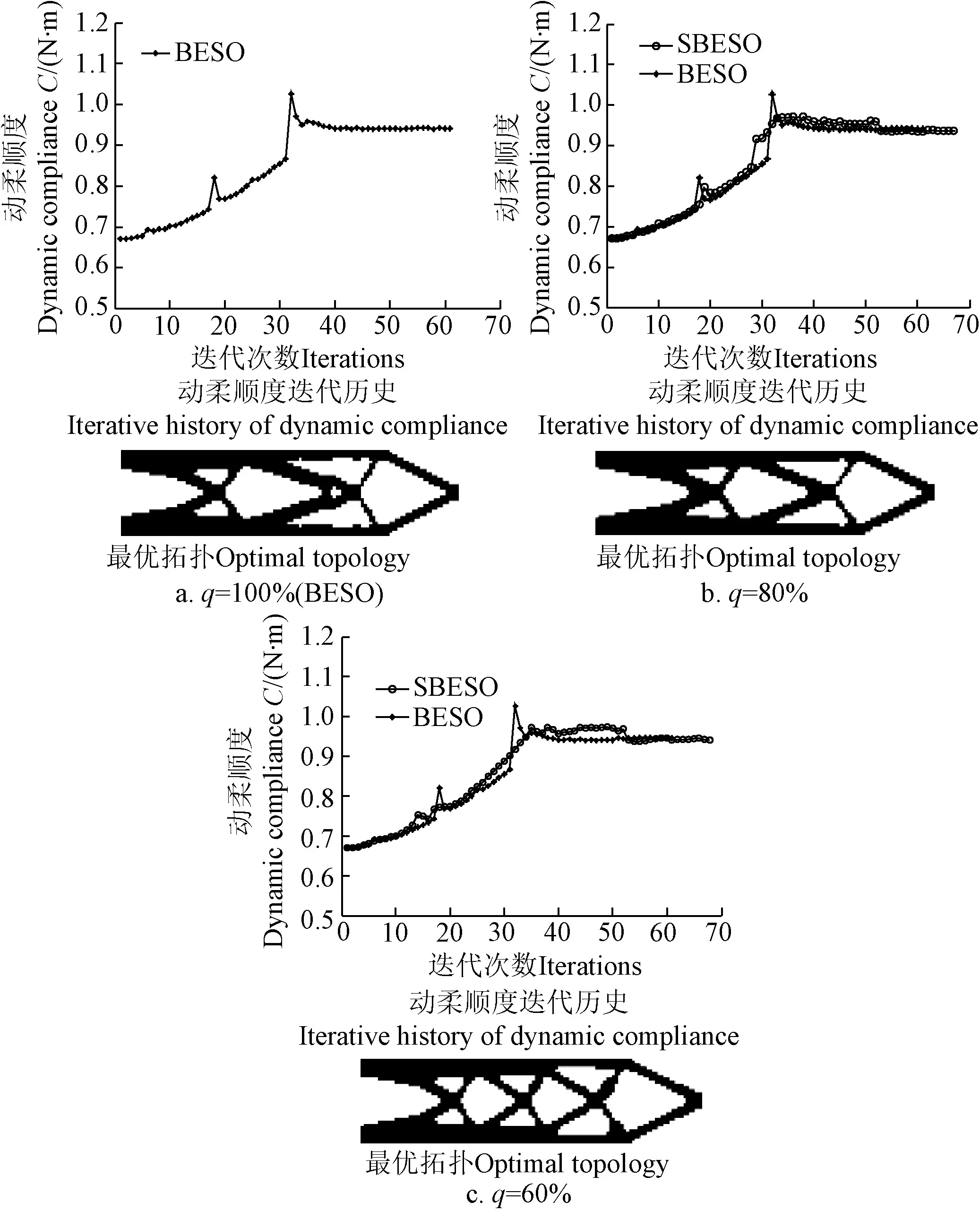
图8 删除率q对动刚度优化拓扑与收敛过程的影响Fig.8 Effect of deletion rate q on optimal topology of dynamic stiffness and corresponding process

4 结 论

针对 BESO方法的单元过删除问题，提出一种低效单元的光滑删除策略，求解了结构频率优化和动刚度优化问题，获得了如下研究结论：

1）研究了一种基于光滑双向渐进结构优化（smooth bi-directional evolutionary structural optimization, SBESO）方法的结构动力学拓扑优化方法。与双向渐进结构优化（bi-directional evolutionary structural optimization, BESO）方法相比，SBESO方法可以调节单元删除率和权重函数，控制低效单元在结构设计域中逐渐被删除，有效抑制了单元的过删除问题，其优化算法具有一定的鲁棒性和适应性。

2）提出了一种基于 SBESO方法的频率优化方法。SBESO方法与BESO方法优化后的频率几乎相等，但是前者随着单元删除率的减少使结构拓扑优化构形逐渐逼近于同一构形。对比分析了权重函数（常函数、线性函数和正弦函）的光滑性对结构优化的影响，线性函数和正弦函数的光滑性强于常函数，致使迭代过程更加光滑，均收敛于同一最优拓扑结构。由此，采用线性和正弦权重函数更有利于获得结构最优拓扑解。

3）将等效静载荷方法与 SBESO方法相融合，提出动载荷作用下结构的动刚度优化方法。能够控制低效单元在优化过程中质量与刚度逐渐趋向于零，进而从设计域中逐渐被删除，同时使得迭代过程中结构拓扑优化构形随单元删除率的减少其结构边界逐渐光滑，而且逼近于同一构形。

因此，本文提出的SBESO方法抑制了BESO方法的过删除问题，进一步完善了 BESO方法的优化准则，对于解决连续体结构动力学优化设计问题具有较为重要的理论意义。